神经网络、深度学习与自然语言处理

冯志伟

摘 要：介绍了自然语言处理中的神经语言模型，讨论了大脑神经网络、人工神经网络、“异或”问题、前馈神经网络、神经网络的历史分期及其进一步发展等;指出，在神经网络的研究中，感知机不能解决线性不可分的分类问题，通过增加隐藏层才能进行“异或”运算。通常情况下，在训练神经网络的同时，还要进行嵌入学习，对于机器翻译、情感分类、句法剖析这些自然语言处理的特殊任务，常常要加上很强的约束，并应当把基于语言规则的理性主义方法和基于大数据的经验主义方法结合起来。

关键词：大脑神经网络;人工神经网络;“异或”问题;感知机;前馈神经网络

中图分类号：TP18  文献标识码：A  文章编号：1004-8634（2021）02-110-（13）

DOI：10.13852/J.CNKI.JSHNU.2021.02.012

语言是观察人类智能的重要窗口，自然语言处理（Natural Language Processing， 缩写NLP）是人工智能皇冠上的明珠。1近年来，特别是2012年以来，神经网络（Neural Network，缩写NN）和深度学习（Deep Learning， 缩写DL）方法在自然语言处理中得到广泛应用，并且逐渐成为自然语言处理研究中的主流技术。

目前，神经网络方法有效提高了自然语言系统的处理水平，把自然语言处理的发展推向了一个崭新的阶段，我们应当加以特别关注。2

神经网络是自然语言处理的一种基本的计算工具，并且是出现得很早的一种工具。之所以叫作“神经”，是因为它源自1943年心理学家麦卡洛克（Warren McCulloch）和数学家皮茨（Walter Pitts）提出的“神经元”（Neuron）。神经元是一种人类神经的可计算单元的简化模型，可以使用命题逻辑（Propositional Logic）来描述。

人工神经网络是由一些小的计算单元构成的网络，神经网络中的每一个单元取一个输入值向量，产生一个输出值。因为人工神经网络在其计算过程中要反复地从神经网络的一个层（Layer）馈入另一层，要穿越若干层，因而是一种有深度的网络，我们常常把这种基于人工神经网络的机器学习（Machine Learning）叫作“深度学习”。

一、大脑神经网络

人类的智能行为都与大脑活动有关。大脑是神经器官，与人体的其他器官（如消化器官、呼吸器官、血液循环器官）不同，它可以产生感觉、知觉和情感。大脑是一个神经系统，由神经元、神经干细胞、神经胶质细胞以及血管组成。神经元能够携带和传输信息，是人脑神经系统中最基本的单元。神经元个数众多，大约有860亿个，它们之间通过上千个突触相连接（神经元之间的连接构成一个巨大的复杂网络，其总长度达数千公里），形成一个极为复杂的神经网络，叫作“大脑神经网络”（Brain Nearal Netwrok）。受到人类大脑神经网络的启发，早期的神经科学家们构造了一种模仿人类大脑神经系统的数学模型（由很多人工神经元组合而成，这些人工神经元之间的连接强度可以通过机器自动学习的方式来自动地获取），叫作“人工神经网络”（Artificial Neural Network）。与大脑神经网络相比，人工神经网络相对要简单得多。

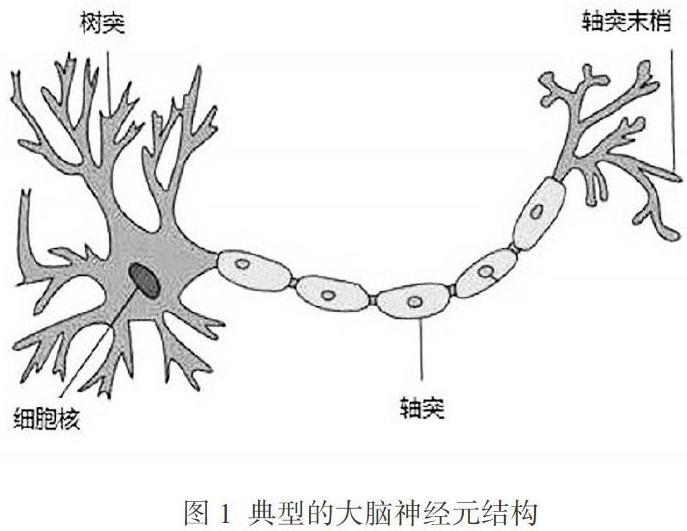
1904年，科学家就已经发现，人类大脑中典型的神经元结构大致可包括细胞体（Soma）、树突（Dendrite）和轴突（Axons）三部分。细胞体主要由细胞核和细胞膜构成，细胞膜上有各种受体（与相应的化学物质神经递质相结合能改变离子的通透性及膜内外电位差，从而使神经细胞产生兴奋或抑制的生理活动）和离子通道。树突和轴突（统称细胞突起，每个神经元可以有一个或多个树突，但轴突只有一个）是从细胞体主体延伸出来的细长部分，前者的功能是接受刺激并将兴奋传入细胞体，后者的功能是把自身的兴奋状态从细胞体由轴突末梢传送到另外的神经元或其他组织。图1是典型的大脑神经元结构。

神经元与神经元之间留有20纳米左右的缝隙，但它们相互间却可以傳递信息。神经元之间的信息传递是靠突触（Synapse，是轴突末梢各分支末端与其他多个神经元的树突相接触形成的，它是神经元之间连接的接口）来完成的。每个神经元只有兴奋和抑制两种状态，由其他神经元的输入信号量及突触抑制或兴奋的强度来决定：当接收到的信号量总和超过了某个阈值时，细胞体就会兴奋，相反就会抑制，从而产生不同强度的电脉冲。一个神经元接收到信息并形成电脉冲后，电脉冲会沿着自己的轴突并通过突触把信息再传递给其他神经元，而其他神经元根据接收到的信号量及突触抑制或兴奋的强度形成自己的状态并产生电脉冲。神经元之间的信息传递就是通过这种方式实现的。

一个人的智力并不是完全由先天的遗传决定的，大部分来自后天的生活经验，是通过在生活中不断地学习而获得的。因此，大脑神经网络是一个具有学习能力的系统，它可以通过不断的学习而得到改进。那么人类大脑是如何进行学习的呢？

大脑神经网络学习的秘诀不在于单个的神经元，而在于神经元之间的连接强度。不同神经元之间突触的信号有强有弱，强的信号会使神经元间的连接增强。通过学习或训练，可以增强突触的信号强度，形成“记忆印痕”，使相关的神经元产生记忆，从而增强这些神经元之间的联系。

1949年，加拿大心理学家赫布（Donald Hebb）提出突触可塑性的基本原理。1他指出，如果两个神经元总是相关联地受到刺激，那么，它们之间的突触强度会增加。举例来说，当A神经元的一个轴突和B神经元接近到足以对其产生影响，并持续、重复地参与对B神经元的兴奋过程，那么，这两个神经元或其中的一个就会发生某种“新陈代谢”的变化，A神经元就成为导致B神经元“兴奋”的一个细胞，从而加强了后者的效能。这个原理叫作“赫布规则”（Hebb Rule）。赫布认为人的大脑有短期和长期两种记忆，短期记忆持续的时间不超过一分钟。如果短期记忆获得的经验重复足够的次数，这个经验就可以长期储存在记忆中，从而转化为长期记忆，这个过程叫作“凝固作用”（人脑中的海马区就是大脑结构凝固作用的核心区域）。

二、人工神经网络

如前所述，人工神经网络本质上是受到大脑神经网络的启发而建立的数学模型。这一模型对大脑神经网络进行抽象来构建人工神经元，并且按照一定的拓扑结构建立起人工神经元之间的连接，从而模拟人类大脑。在人工智能领域，人工神经网络也常常简称为“神经网络”或“神经模型”（Neural Model，缩写NM）。人工神经网络从结构、实现机理和功能等方面来模拟人类大脑神经网络，其结构如图2所示。从第一个神经元的轴突传送的信息x0经过突触时，被赋予了权重w0，以w0x0的值传送到当前神经元的树突，进入细胞体。同样，从第二个神经元的轴突传送的信息x1经过突触时，被赋予了权重w1，以w1x1的值传送到当前神经元的树突，进入细胞体;从第三个神经元的轴突传送的信息x2经过突触时，被赋予了权重w2，以w2x2的值传送到当前神经元的树突，进入细胞体;从第i个神经元的轴突传送的信息xi经过突触时，被赋予了权重wi，以wixi的值传送到当前神经元的树突，进入细胞体。

在细胞体有一个激励函数（Activation Function），记为f，这个激励函数控制着wixi，当wixi的值大于某一个阈值时输出1，否则输出0，这样，在这个神经元的轴突上，便可以得到一个被激励函数f控制的输出（Output Axon）：

其中，wi表示权重，xi表示输入信息，b表示偏置（Bias）。

人工神经网络模仿大脑神经网络中神经元的原理，由若干个人工神经元相互连接而成，可以用来对各种数据之间的复杂关系进行建模。建模的时候，给不同人工神经元之间的连接赋予不同的权重，每个权重代表一个人工神经元对另一个人工神经元影响的强度。每一个神经元可以表示一个特定的函数，来自其他人工神经元的信息经过与之相应的权重综合计算，输入到一个激励函数中并得到一个表示兴奋或抑制的新值。

从系统的观点来看，人工神经网络是由大量的神经元通过非常丰富和完善的连接而构成的自适应非线性动态系统（Self-adaptive Non-linear Dynamic System）。

尽管我们能够比较容易地构造一个人工神经网络，但是如何让这样的人工神经网络具备自动学习的能力并不是一件容易的事情。

早期的神经网络模型并不具备自动学习的能力。第一个可以自动学习的人工神经网络是赫布网络（Hebb Network），它采用了一种基于赫布规则的无监督机器学习算法（Unsupervised Machine Learning Algorithm）。感知机（Perceptron）是最早的具有机器自动学习能力的神经网络，但是它的自动学习方法无法扩展到多层神经网络上（详见后文）。直到1980年前后反向传播算法（Back Propagation Algorithm，简称BP算法）提出后，才有效地解决了多层神经网络的自动学习问题，而反向传播算法也就成为最为流行的神经网络自动学习算法。

人工神经网络诞生之初并不关注机器自动学习问题。由于人工神经网络可以被看作一个通用的函数逼近器，一个具有两个层级的人工神经网络可以逼近任意函数，因此，人工神经网络就可以被看作一个可以进行自动学习的函数，并能够应用到机器自动学习中。从理论上说，人工神经网络只要具有足够数量的训练数据和神经元，就可以自动地学习到很多复杂的函数。人工神经网络模型自动学习任何函数能力的大小叫作网络容量（Network Capacity），网络容量的大小与存储在网络中信息的复杂程度以及数量的多少有关。

神经网络最早是一种连接主义模型（Connectionism Model）。20世纪80年代后期，最为流行的连接主义模型是分布式并行处理（Parallel Distributed Processing，缩写PDP）网络。

这种分布式并行处理网络有3个主要特性：它的信息表示是分布式的;它的记忆和知識存储都是通过单元与单元之间的连接来进行的;它要通过逐渐改变单元与单元之间的连接强度来自动地学习新的知识。

连接主义的人工神经网络有着多种多样的网络结构和机器自动学习的方法。虽然早期的人工神经网络强调模型的生物可解释性（Biological Plausibility），但后期更关注对某种特定认知能力的模拟，比如物体识别、自然语言理解等。尤其在引入反向传播算法来改进其学习能力后，人工神经网络也越来越多地应用于各种模式识别（Pattern Recognition）任务中。随着训练数据的增多以及并行计算能力的增强，人工神经网络在很多模式识别的任务中已经取得了很大的突破，特别是在语音、图像等感知信号的处理上，人工神经网络表现出了卓越的自动学习能力。

从机器自动学习的角度来看，人工神经网络可以被看作一个非线性模型，它的基本组成单元是具有非线性激活函数的神经元，通过大量神经元间的连接，使得人工神经网络成为一种高度的非线性模型。神经元间的连接权重就是需要机器自动学习的参数，这些参数可以通过梯度下降（Gradient Descent）的方法来进行自动学习。

1957年，美国康奈尔航天实验室的心理学家罗森布拉特（Frank Rosenblatt）根据大脑神经元的原理与赫布规则，建立了感知机的数学模型。感知机是最简单的人工神经网络，它只有一个神经元。

感知机作为简化的数学模型可以解释大脑神经元是如何工作的，它从附近的神经元中取一组输入值x1，x2，x3，…… xi，将每个输入值乘以一个连续值权重w1，w2，w3， ……wi，这个权重也就是每个附近的神经元突触的强度，输入信息可以表示为：

感知机还要为偏置设立一个阈值θ。如果加权输入值的和超过了这个阈值θ，那么，就输出1，这时，y=1，神经元兴奋;如果加权输入值的和等于或者低于这个阈值θ，那么，就输出0，这时，y=0，神经元抑制。如图3所示。

有了这样的神经元，感知机就可以对操作对象进行线性分类（Linear Classification）了。因此，感知机是一种简单的线性分类模型。

感知机是对大脑神经网络简单的数学模拟，它有与大脑神经网络的神经元相对应的部件，其权重wi相当于大脑神经网络神经元的突触，阈值θ的控制机制相当于大脑神经网络细胞体的功能。这样的感知机是具有自动学习能力的。

通过调整感知机输入值的权重，可以提出一个非常简单而直观的机器自动学习方案：给定一个有输入输出实例的训练集，感知机从实例中自动地学习一个激励函数f（对每个实例，如果感知机的输出值比实例低，则增加它的权重;如果感知机的输出值比实例高，则减少它的权重）。

具体的机器学习算法如下：（1）从感知机的随机权重以及一个训练集开始。（2）对训练集中一个实例的输入值x1， x2， x3， x4，…… 计算感知机的输出值y1。（3）如果感知机的输出值与实例中默认正确的输出值不同，则做如下处理：若输出值应该为0但实际为1，则减少输入值实例的权重;若输出值应该为1但实际为0，则增加输入值实例的权重。（4）对训练集中下一个实例执行同样的操作，重复步骤（2）—（4），直到感知机不再出错为止。如图4所示，输入（Input）x1， x2， x3， x4，……由感知机的神经元激励函数f控制，得到输出y1。

罗森布拉特根据感知机的数学原理，制造出了感知机的硬件，这种感知机可以用来对20×20像素输入中的简单形状进行正确分类。这台感知机硬件可以从已知的“输入—输出”偶对中得出近似函数，因而实现了机器学习，这是世界上第一台可以进行机器学习的计算机。尽管当时它只学习了一些简单的函数，但是由此不难想象它广阔的应用前景。罗森布拉特用他的感知机自动地识别了手写体的阿拉伯数字，这是世界上首次实现的自动文字识别。

罗森布拉特最早提出了两类感知机算法，随后又给出了感知机收敛定理。但是由于感知机的输出是离散的，其学习算法还比较简单，限制了其应用范围。

1969年，明斯基（Minsky）和帕佩特（Seymour Papert）在《感知机：计算几何导论》一书中分析了感知机的局限性，指出感知机存在如下两个关键问题：1第一，感知机不能解决线性不可分的分类问题（“异或”问题，在现实生活中广泛存在）。第二，训练以感知机为基础的实用神经网络模型需要庞大的计算资源和计算能力，当时的技术条件还不具备现实可行性。在这种情况下，感知机的研究进入了十多年的“低谷”。

三、“异或”问题

如前所述，明斯基和帕佩特指出，像感知机这样的单独的神经元不能计算输入它的某些简单的非线性函数，即“异或”（XOR）函数，这个函数是线性不可分的。

我们来考虑有两个输入x1和x2的逻辑函数的计算问题，AND运算（“与”运算）、OR运算（“或”运算）和XOR运算的真值表如图5：

感知机可以进行AND运算和OR运算，但明斯基和帕佩特证明了不可能构造一个感知机来进行XOR运算。然而，XOR运算在实际生活中是常见的。例如，在自然界和人类社会中的“同性相斥、异性相吸”的现象，其逻辑原理就是XOR运算，此类问题在实际生活中屡见不鲜。在逻辑上，XOR運算是一个线性不可分问题，而感知机不能解决这样的线性不可分问题，这是感知机的一个严重缺陷。

图6显示了AND运算和OR运算的可能的逻辑输入（00， 01， 10和11），以及根据一组参数画出的分界直线。用实心圆点表示正值（Positive Value），用空心圆点表示负值（Negative Value）。这时，AND运算和OR运算都能够把运算结果做出正确的分类，把实心圆点置于分类线的一侧，而把空心圆点置于分类线的另一侧。但是，不存在一种简单的方法可以画出一条直线把XOR运算的实心圆点（01和10的“异或”运算得出的正值）和空心圆点（00和11的“异或”运算得出的负值）分割开来。因此，XOR这个函数不是一个线性可分函数（Linearly Separable Function），也就是说，XOR函数是线性不可分的。当然，也可以用曲线或者其他的函数给实心圆点和空心圆点勉强画出一条分界线，但是，这已经不是一条单独的直线了。

明斯基和帕佩特尖锐地指出了感知机的这种缺陷，他们的书出版后引起了很大反响。于是，学术界认识到感知机不能处理日常生活中很常见的XOR运算的线性不可分问题，因此，他们对于感知机的热望一落千丈。这给感知器以及人工神经网络研究的热潮泼了一瓢冷水，也使得公众对于人工神经网络的期望降到了冰点。

那么，怎样才能解决XOR运算的线性不可分问题呢？科学家们提出了给感知机设置“隐藏层”（Hidden Layer）的聪明办法。2

如果在感知机中设置隐藏层h1和h2，如图7所示（箭头上的数字表示每一个神经元的权值w，偏置b表示在+1处的一个权值，偏置的权值和神经元都用浅灰色表示），加入了隐藏层之后，可以使感知机形成一种新的表示，从而解决了线性不可分问题。对于隐藏层h1和h2，当输入点为x1=[1  1]和x2=[1  1]的时候，其结果通过隐藏层在输出y1处融合为一个单独的点，使得它们的计算结果在y1处都为负值（也就是为0），从而解决线性不可分问题。这样，加了隐藏层的感知机就可以进行“异或”运算了。下面我们进一步解释“异或”运算问题。

图8比较了没有加隐藏层的x空间和加了隐藏层的h空间的不同情况。左侧a）表示原来的x空间（The Original x Space），右侧b）表示加了隐藏层之后的新的h空间（The New h Space）。可以看出，在进行XOR运算时，在原来的x空间中，当x=[1  0]与x=[0  1]时，其输出值分别处于x0和x1轴上，都为1;而当x=[0  0]与x=[1  1]时，其输出值不能处于除了原点之外的x0和x1轴上，都为0，这样就没法对它们进行线性分割。在加了隐藏层的h空间中，可以把网络的隐藏层看作形成了一种新的输入表示，输入点x=[1  0]和x=[0  1]的隐藏代表改变为h=[1  0]的输出值与h=[0  1]的输出值，这时它们的输出值都融合为一个单独的点h=[1  0]了。这样，由于增加了隐藏层，融合之后就容易对XOR的负值（用空心圆点表示）和正值（用实心圆点表示）线性地进行分割了。

在上面图7的例子中显示了一些权重的值，但实际上，神经网络的权重是通过“反向传播算法”来自动学习到的。这就意味着，隐藏层要通过“深度学习”才能形成有用的表示。神经网络有能力自动地从输入中学习到有用的表示，这是人工神经网络最为关键的优点。

“异或”问题的求解要求神经网络带有非线性的激活函数，因此，只由一个简单的线性神经元（感知机）构成的神经网络是不能解决“异或”问题的。需要给感知机增加一个或多个隐藏层，把单层的感知机进一步扩充为多层次的感知机，通过多个层次来进行深度学习，就可以解决“异或”这样的线性不可分问题了。显而易见，给感知机增加隐藏层这样的聪明办法，大大地增强了感知机的效能。

四、前馈神经网络

直到1980年后，辛顿（Geoffrey Hinton）、乐坤（Yann LeCun）等人才改进了感知机，给其增加隐藏层，把它改造成多层的感知机（Multi-Layer Perceptron，缩写MLP），使之具有处理线性不可分问题的能力。他们还用连续的输出代替离散的输出，并采用反向传播算法进行权重的自动学习，把反向传播算法引入多层感知机中，这样的多层感知机就可以进行深度学习了，感知机的研究又重新引起人们的关注。明斯基等人也修正了他们的看法，开始大力支持感知机的研究。

与此同时，人们对感知机本身的认识也在不断发展。1999年，弗勒伊德（Freund）和沙皮尔（Schapire）提出了使用核技巧来改进多层感知机的深度学习算法，并使用投票感知机来提高多层感知机的泛化能力。2002年，科林斯（Collins）将多层感知机算法扩展到结构化的深度学习中，给出了相应的收敛性证明，并且提出一种更加有效和实用的参数平均化策略。2010年，麦当纳（McDonald）又扩展了平均感知机算法，使得多层感知机可以在分布式计算环境中进行并行计算，这样就能使用多层感知机来进行大规模的深度学习了。

到目前为止，研究者已经提出了许多结构各不相同的人工神经网络。它们都是在感知机的基础上发展起来的。作为例子，在本文中介绍一种有代表性的人工神经网络——“前馈神经网络”（Feed-forward Neural Network，缩写FNN）。不同的人工神经网络有着不同网络连接的拓扑结构，比较直接的拓扑结构是前馈网络，它是最早提出的多层的人工神经网络。

在前馈神经网络中，每一个神经元分别属于不同的层，每一层的神经元可以接收前一层神经元的信号，并产生信号输出到下一层的神经元。第0层神经元叫输入层（Input Layer），最后一层神经元叫输出层（Output Layer），其他处于中间层次的神经元叫隐藏层。整个网络中没有反馈，信号x1， x2， x3， x4从输入层输入，经过隐藏层，向输出层进行单向传播，最后在输出层输出结果y1，y2，y3，形成一个有向非成圈图。这种前馈神经网络有若干个隐藏层，所以也叫多层感知机。前馈神经网络中相邻两层的神经元之间是全連接关系，也称为“全连接神经网络”（Fully Connected Neural Network，缩写FCNN）。其结构如图9所示。

也可以把这样的前馈神经网络看作一个复合函数（Complex Function），它通过简单非线性函数的多次复合，实现输入空间到输出空间的复杂映射。这种网络的结构简单，易于实现。

前馈神经网络作为一种能力很强的非线性模型，在20世纪80年代后期就已被广泛使用，但是基本上都是三层网络（只有一个输入层、一个隐藏层和一个输出层），虽然当时前馈神经网络的参数学习依然有很多难点，但它可以作为连接主义的一个典型模型，标志着人工智能从高度符号化的知识期向低符号化的深度学习期的转变。这是人工智能研究中的重要转折点。

在前馈神经网络中，每个神经元包括两部分：一部分负责线性加权求和，叫作“线性层”;另外一部分是激励函数，由于激励函数都被定义为非线性的，所以又叫作“非线性层”。单层的感知机中同样可以使用激励函数，但是由于是否使用激励函数并不影响单层感知机的分类能力，因而往往被忽略。然而在多层感知机中，激励函数对于神经网络的深度学习能力具有至关重要的作用;如果在两个网络层之间没有非线性的激励函数，不论网络有多少层，总体上仍然等价于一个线性函数，从数学的角度看，与单层感知机的表达能力并没有什么不同，难以处理线性不可分问题。由此可见，激励函数大大改善了前馈神经网络的性能。

在理论上可以证明，只要激励函数能够满足特定的宽松条件，那么，对于任何一个连续函数，都存在一个有限大小而且至少包含一个隐藏层的神经网络，因而就能够以任意的精度逼近这个连续函数。

在前馈神经网络中，输出层的作用是取隐藏层的表示，并计算出最后的输出。这个输出可能是一个实数，但是在很多场合下，神经网络的目标是进行某种分类判定，所以，现在把问题的焦点集中到分类（classification）这样的场合。

在自然语言处理中，如果用前馈神经网络来做文本的情感分类这样简单的二元分类，那么可得到一个单独的输出，而它的值就是正面情感对于负面情感的概率值。如果做多元的分类，例如，给文本指派不同的词类标记（Tag of POS），那么，对每一个潜在的词类都会得到输出节点，而在输出节点上的输出值就是这个词类标记的概率，并且所有这些输出节点的概率值的总和为1，因此，在输出层就可以在所有的节点上给出概率分布。

在神经语言模型（Neural Language Model）中，前面的上下文是使用前面单词的词嵌入（Word Embedding）来表示的。把前面的上下文表示为词嵌入，而不是像在N元语法模型（N-gram Model）中那样表示为精确的、具体的单词，这就使得神经语言模型能够泛化为“看不见的数据”（Unseen Data），对于自然语言描述的抽象程度更高，显然比N元语法模型具有更强的功能。例如，在训练集中可以看到这样的句子：

I have to make sure when I get home to feed the cat.

在feed the 这样的单词串之后是单词cat。如果在测试集中试图预测在前面出现另外的单词系列I forgot when I got home to feed the之后，究竟会出现什么单词，应当怎么办呢？

根据训练集的例子，如果使用N元语法模型，就可以预见到feed the之后的单词应当是cat，而不会是单词dog。如果使用一个神经语言模型，那么，这个神经语言模型就可以根据cat和dog具有相似的嵌入（Embedding）这样的事实，理直气壮地给dog指派与cat一样高的概率，从而判断feed the后面的单词可能是dog，而做出这种判断的根据就仅仅是因为它们在嵌入中具有相似的词向量。由此可以看到，神经语言模型确实比N元语法模型更胜一筹。1

来看一看前馈神经语言模型在实际上是怎样工作的。假定有一部嵌入词典（Embedding Dictionary）E，对于普通词典V中的每一个单词，嵌入词典E都能给出相应单词的词向量嵌入（Word Vector Embedding，可以使用word2vec算法预先计算出来），这样，在自然语言处理中就可以直接从嵌入词典中查询到单词的词向量。2

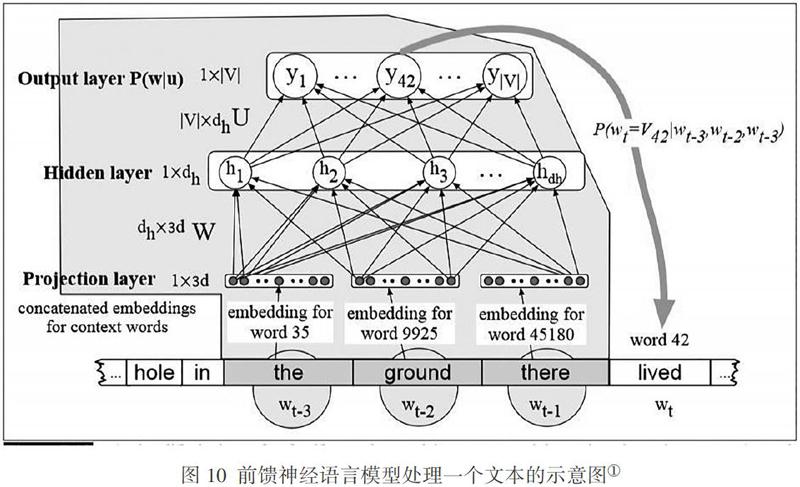
图10是前馈神经网络模型处理一个文本的示意图，描述了一个简化的前馈神经语言模型的梗概，这个模型的N=3，在时间点t有一个移动窗口以及单词wt前面3个单词（单词[wt-1，wt-2，wt-3]）的嵌入向量。这3个向量毗连起来构成神经网络的输入层x，神经网络的输出是这些单词的概率分布，因此，在输出节点42上的值y42就是下面标为V42的单词（即词典中标引号为42的单词，在这里是lived）的wt的概率。

显而易见，这个图是被简化了的，因为对图中的每一个单词都已经查找出了它在嵌入词典E中的d维嵌入向量，而且事先使用诸如word2vec这样的算法进行了预先的计算。不过，在通常情况下，在训练神经网络的同时，还要进行嵌入学习（Embeddding Learning）;而且在设计神经网络的时候，对于机器翻译、情感分类、句法剖析这些自然语言处理的特殊任务，常常要加上一些很强的约束以使输入的表示更加完美。

五、人工神经网络的分期及其进一步发展

人工神经网络的发展大致可以分为五个阶段：萌芽创业期、第一个低潮期、复苏振兴期、第二个低潮期、崛起繁荣期。2

萌芽创业期为1943—1969年，是人工神经网络发展的第一个高潮期。这个时期，科学家们提出了许多神经元模型。如1943年麦卡洛克和数学家皮茨构建的MP模型，1948年图灵（Allen Turing）描述的“图灵机”（Turing Machine），1951年明斯基建造的第一台模拟神经网络的机器SNARC，1958年罗森布拉特提出的可以模拟人类感知能力的神经网络模型——“感知机”等。这一时期，人工神经网络以其独特的结构和处理信息的方法，在自动控制、模式识别等应用领域中取得了初步的成效。

第一个低潮期为1969—1983年，人工神经网络第一次落入低谷。在此期间，受1969年明斯基和帕佩特《感知机：计算几何导论》的影响，人工神经网络的研究处于长达15年的停滞状态。虽然1974 年哈佛大学的魏博思（Paul Webos） 发明了反向传播算法，但当时未受到应有的重视。1980年，福岛邦彦（Fukushima）提出的一种带卷积和子采样操作的多层神经网络——“新知机”（Neocognitron），没有采用反向传播算法，而是采用了无监督机器学习的方式来训练，因此也没有引起学术界的重视。这就使得人工神经网络的研究长期处于低潮状态。

复苏振兴期为1983—1995年，是人工神经网络发展的第二个高潮期。其间，由于给感知机添加隐藏层解决了线性不可分问题，反向传播算法重新激发了人们对人工神经网络的兴趣。1983年，美国加州理工学院的物理学家何普菲尔德（John Hopfield）提出了一种用于联想记忆以及优化计算的人工神经网络，称为“何普菲尔德网络”（Hopfield Network），其在解决“旅行商问题”上获得当时最好的结果，引起了轰动，促进了人工神经网络研究的复苏。1984年，辛顿提出一种随机化版本的何普菲尔德网络，即“玻尔兹曼机”（Boltzmann Machine）。真正推动人工神经网络振兴的是反向传播算法。1986年，鲁迈哈特（David Rumelhart）和麦克兰德（James McClelland）对于连接主义在计算机模拟神经活动中的应用进行了全面研究，改进了反向传播算法。辛顿等人将反向传播算法引入多层感知机的研制中，于是人工神经网络又重新引起人们的关注，成为人工智能研究中的新热点。随后，乐坤等人将反向传播算法引入“卷积神经网络”（Convolutional Neural Network，缩写CNN）中，并应用在手写体数字自动识别方面，降低了误识率，推动了人工神经网络的研究。可是好景不長，人工神经网络不久就进入了第二个低潮期。

第二个低潮期为1995—2006年，持续达11年之久。在这期间，基于统计的“支持向量机”（Support Vector Machine，缩写SVM）和其他更简单的统计方法（例如线性分类器）在机器学习领域的流行度逐渐超过了人工神经网络。虽然人工神经网络可以通过增加神经元数量的方式来构建复杂的网络，但其计算复杂性也随之呈指数级增长，当时的计算机性能和数据资源的规模都不足以支持训练大规模的人工神经网络。在20世纪90年代中期，统计机器学习理论和以支持向量机为代表的机器学习研究在自然语言处理中独占鳌头，而人工神经网络则相形见绌，它的理论基础不够扎实、优化比较困难、可解释性差等缺点更加凸显出来，于是，人工神经网络的研究又一次跌入了低谷。

崛起繁荣期为2006年以后至今。2006年，辛顿和萨拉库提诺夫（Salakhutdinov）研制了多层前馈神经网络，通过逐层预训练（Pre-training），再使用反向传播算法进行微调（Fine-tuning），取得了很好的机器学习效果，从而使人工神经网络研究迈出低谷、再次崛起，并且逐渐走向了繁荣，推动了人工智能的大发展。随着深度的人工神经网络在语音识别、图像分类、机器翻译、智能问答等应用领域中的巨大成功，以人工神经网络为基础的深度学习迅速崛起。近年来，随着大规模并行计算以及GPU（Graphic Processing Unit）设备的普及，计算机的计算能力得到大幅度提高，可供机器学习的数据资源的规模也越来越大。在算力、算法和大数据算料资源的支持下，計算机已经具备了训练大规模人工神经网络的能力，于是，各大科技公司纷纷投入巨资来研究深度学习，人工神经网络研究进入它的第三个高潮期。深度学习需要在大规模真实的语料库（算料）的基础上进行，这对资源丰富的语言（如英语、汉语、法语）来说，可以取得显著的成效，可是，对于那些资源贫乏的语言（如藏语、维吾尔语、彝语）来说，由于缺乏充足的语言数据，难以保证深度学习的效果。为此，在深度学习的基础上，自然语言处理中就提出了“迁移学习”（Transfer Learning）和“预训练”问题。于是，除了深度学习这种模型外，自然语言处理中又出现了一个新的模型 ——“预训练模型”（Pre-training Model），它不仅使得多种自然语言处理的任务达到了新的高度，而且大大降低了自然语言处理模型在实际应用场景中落地的门槛。为了衡量计算机理解自然语言的能力，美国华盛顿大学、Facebook和DeepMind等机构在2019年提出了人工智能基准测试的一个项目SuperGlue，其任务包括智能问答、语言推理、词义排歧、指代消减等。在最近的SuperGlue测试中，微软公司的DeBERTa模型和谷歌公司的T5+Meena模型都取得了很好的成绩，有的指标甚至超过了人类的基准线。

综上，人工神经网络的发展经历了一个由高潮和低潮交互而成的马鞍形曲折过程：萌芽创业期à 第一个低潮期à 复苏振兴期à 第二个低潮期à 崛起繁荣期。

现如今，人工神经网络正处于其发展的第三个高潮期中。尽管人工神经网络在数学上是完美的，可是它的运行机理却不容易从语言学和普通常识的角度得到理性的解释，而且人工神经网络也难以应用人类在长期的语言学研究中积累起来的丰富多彩的语言知识来改进自身的不足。为了进一步推动自然语言处理的发展，决不能忽视人类在历史长河中积累的语言知识和语言规则，应当把基于语言规则的理性主义方法（Rationalism Approach）与基于语言大数据的经验主义方法（Empiricism Approach）结合起来，使用语言规则来弥补人工神经网络的不足。换句话说，在自然语言处理研究中，在大力推广人工神经网络的经验主义方法的同时，也要逐步复兴近年来受到冷落的理性主义方法，让神经网络从语言的理性规则中吸取营养，不断完善，增强它的可解释性。1目前流行的深度学习的热潮为自然语言处理中基于语言大数据的经验主义方法添了一把火，预计这样的热潮还会继续主导自然语言处理领域很多年。然而，在自然语言处理的研究中，基于语言规则的理性主义方法复兴的历史步伐是不会改变的，基于语言数据的经验主义方法一定要与基于语言规则的理性主义方法结合起来，才是自然语言处理的必由之途，也是当代人工智能研究的金光大道。

（责任编辑：苏建军）