大位宽情况下的回滚式循环冗余校验算法
罗 宇 郭家松
①(北京交通大学经济管理学院 北京 100044)
②(北京交通大学离退休干部处 北京 100044)
1 概述
循环冗余校验( Cyclic Redundancy Check,CRC)易于实现,且具有较优的误码检错能力和抗干扰性能被广泛应用于高速网络的差错控制中[1],以太网,ATM, PCIe, PON和OTN等数据通信协议中都使用了CRC算法。CRC还可以和其它编码技术结合,例如LDPC码与Polar码,形成新的编码技术[2]。CRC校验需要对每个报文的全部内容进行数据校验,运算频繁,为了不影响吞吐量和转发速度,一般都是采用硬件算法实现[3]。通常采用异或门逻辑算法[4],或者查表算法[5]。
随着数据通信带宽的不断提升,受器件工作频率的限制,器件内部的数据位宽也越来越宽,以以太网硬件为例,早期千兆以太网的时候,理论带宽只有1000 Mbps,如果主频是125 MHz的话,数据位宽只要8 bit就够了(1000/125=8)。而现在100 Gbit以太网已经普及,在这种情况下,即使工作频率提升到400 MHz,数据位宽也需要增加到256 bit,才可以达到百G以太网的理论带宽。
CRC算法也从串行实现变成了并行实现,CRC校验算法可以通过递推的方法从串行形式推导出并行形式[6]。
查表法CRC虽然可以比较简单地提高运算性能[7],但是需要占用存储单元,占用空间随着位宽加大指数上升,因此需要用逻辑门算法。
随着输入位宽的不断提升,CRC并行运算的要求也越来越高。对于并行逻辑门CRC的算法,在文献[8,9]中,给出了多种实现方案。并行数据位宽加大的情况下,也带来了逻辑门级数增多,延时加大,限制工作频率的问题,不过可以通过加流水线(pipeline)优化的方式[10]或分段运算-拼接[11]来解决。
但是在大位宽并行输入的情况下,又引入了一个问题:那就是报文尾计算的问题。
问题的引出是这样的:数据报文的长度都是整数字节的,但是报文长度的总字节数是不固定的。在8 bit数据位宽时,因为报文长度是整数字节,所以每次CRC计算的输入数据长度是固定的8 bit;但是在更大位宽情况下,报文的最后一拍有效数据位数是不定的,存在末尾的某些字节无效的情况,这也就导致做CRC运算时最后一拍的输入数据位宽是不定的。
以32 bit(4 Byte)的位宽为例,如图1所示,一个长度为18 Byte的报文,需要传输5个时钟周期。前4个周期里,每周期有4 Byte有效数据,最后一周期,只有2 Byte有效数据。
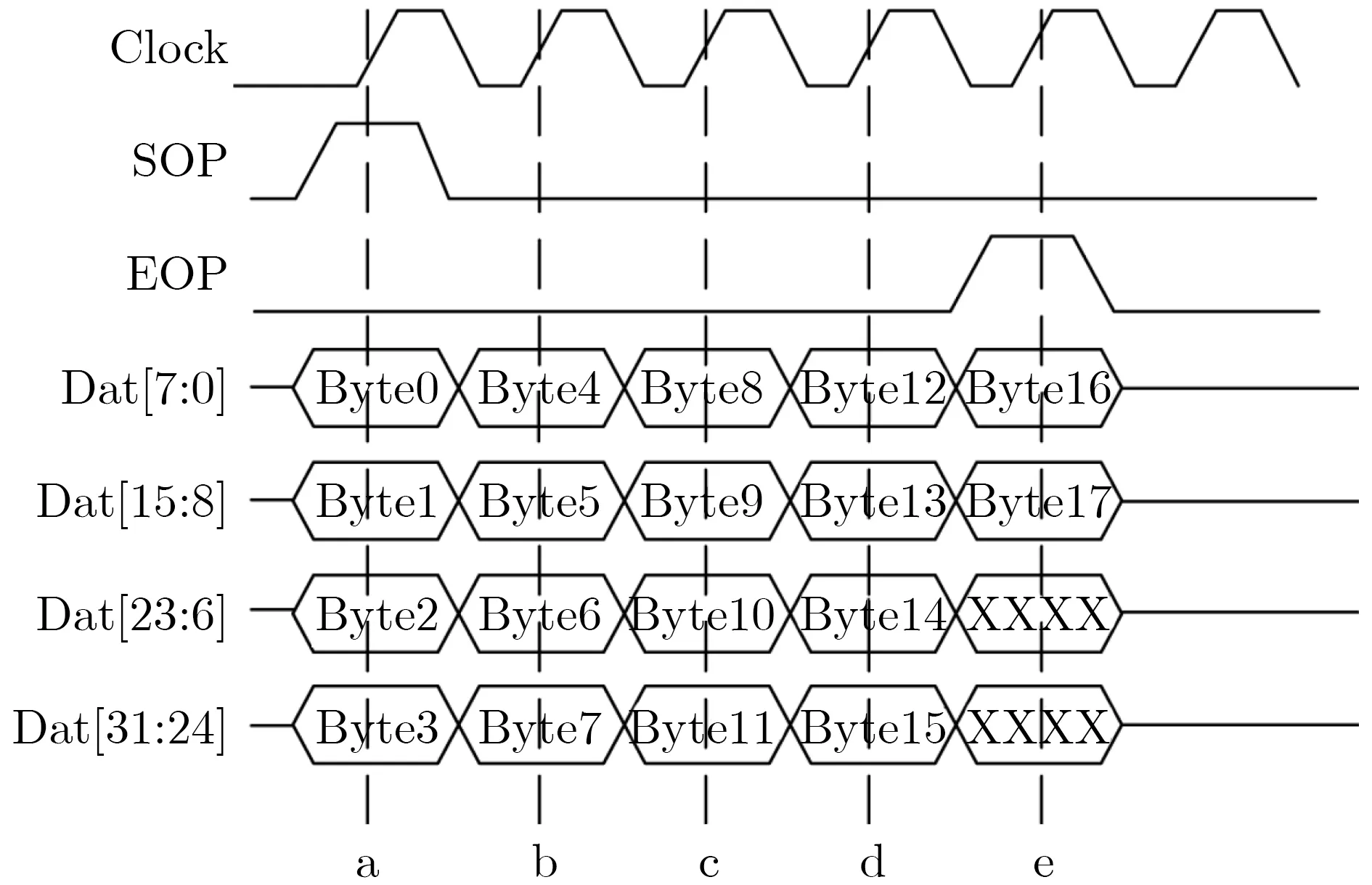
图1 报文尾有无效字节
CRC算法需要对整个报文做校验,所以前4个周期里,每个周期计算4 Byte,最后一周期,只计算2 Byte,而末尾的2 Byte无效字节是不被计算的。因此最后一周期,CRC算法模块输入数据位数和前4周期是不一样的。随着报文长度的变化,最后一周期的输入位宽有4种可能(1~3 Byte)。
文献[12]提供了一种可变数据位宽的CRC运算方法,可以灵活的处理不同输入数据位宽的CRC运算。但是此种变位宽CRC运算是串行的,一个时钟周期只能处理1 bit,而我们要求的处理速度是在一个时钟周期内处理完数据位宽的所有bit。此算法性能远远不能满足要求。
为应对上述情况,在常规的设计实现中,需要放置多个不同CRC算法模块,对应不同字节的输入位宽,然后根据最后一周期的实际有效数据个数,选择相应模块的输出作为最终的CRC校验值[13,14]。很多设计都采用了这种方法来解决尾部数据变长的问题,例如文献[13]和文献[14],其CRC部分实现如图2,图中的数据位宽是64 bit(8 Byte),是个标准的常规设计。
这样的传统实现方式消耗资源较多,在位宽不很大的情况下(如4 Byte, 8 Byte)还可以接受,但是在更大数据位宽情况下,如32 Byte及以上,会消耗大量的逻辑资源,处理带宽越高,数据位宽也就越宽,这样的资源消耗也就越严重。
文献[15,16]中提供了一种级联结构的实现方式,可以在10 Gbit以太网情况下比较经济地完成CRC校验功能,但是在更大位宽的100 Gbit以太网中,依然存在级联级数多,时延不均衡的问题。
2 CRC回滚计算的思路
因为传统实现方案的缺陷,可以以一种新的算法来代替原有的算法。
2.1 数据回滚
CRC运算是通过输入数据和上一次的CRC结果数据做异或运算得到的,是一种线性运算,可以用矩阵的方式来表示[11],例如一个输入数据位宽为8 bit(1 Byte)的CRC32运算模块,输入变量有2个:8 bit输入数据D, 32 bit的上一次运算值CRC32-1;输出变量有1个:32 bit输出值CRC32,这些变量都以向量的方式表示:CRC32=[c31c30··· c1c0],D =[d7d6··· d1d0],CRC32-1=[cl31cl30···cl1cl0] 。
则可以表示为运算式


图2 传统实现
式(1)简化写做
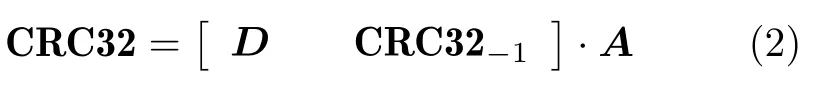
A是一个40行32列的矩阵,是CRC算法的生成矩阵,是一个常数矩阵。
对于一个M Byte输入数据位宽的CRC运算模块,在最后一周期的CRC运算中,如果M Byte中的最后n Byte是无效数据,而我们依然把所有数据都输入给CRC算法模块,那么计算的结果肯定是错的。这个错误的CRC32值(记作CRC32E),是正确的CRC32值(记作CRC32C)在多计算了末尾的n个无效数据字节后得到的。如果通过某种运算,把这n个无效数据字节逆运算回去,就能得到正确的CRC32C值。因为CRC运算是矩阵运算,我们首先想到的逆运算方法就是逆矩阵。但是式(2)中的运算矩阵A不是方阵,不存在逆矩阵。不过如果在计算CRC32E时,令末尾的无效数据字节D为全0(这在设计中很容易实现):D=[0 0 ··· 0 0]。将其代入式(1)后,式(1)可以变为

式(3)可简化写做
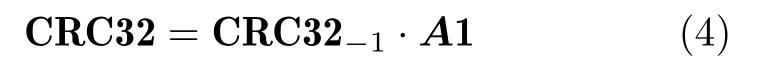
式(4)中A1是一个32行32列的方阵,可能存在逆矩阵。
此时,对于上述包含n个末尾无效字节(已令其为全0)数据的CRC运算,可以表示为
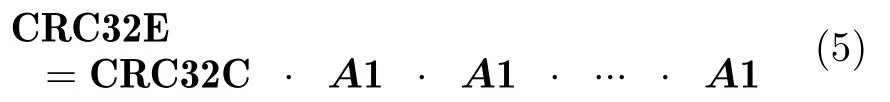
式(5)中,矩阵A1的数量为n个。
这样的话,就可以通过逆矩阵反运算得到正确的CRC32C:CRC32E·A1-1·A1-1· ··· ·A1-1=(CRC32C·A1·A1 · ··· · A1)·A1-1·A1-1· ··· ·A1-1=CRC32C
2.2 二进制运算的矩阵求逆
CRC算法中,采用的都是二进制的布尔运算,算法中都是线性运算,即只涉及到加法和乘法,但布尔运算和普通的数学运算有一些不同:
数据:只有0和1两个值;
加法:0+0=0, 0+1=1, 1+0=1, 1+1=0;
乘法:0×0=0, 0×1=0, 1×0=0, 1×1=1。
可以看出,只有布尔运算的加法和普通的数学运算不同,只要做一些小调整,就可以使用常规的方法完成布尔矩阵的运算。算得的结果中,只需要把结果进行二值化处理,即:奇数都变成1,偶数都变成0就行了。
为了避免繁琐枯燥而易错的手工矩阵运算,在这里,我们采用的开源的数学工具Maxima进行矩阵运算。
要计算8 bit的全0数据输入的运算矩阵A1,首先构造1 bit的0数据输入运算矩阵Ab:CRC32=CRC32-1·AbCRC32的生成多项式为:G(x)=x32+x26+x23+x22+x16+x12+x11+x10+x8+x7+x5+x4+x2+x+1[10];可以写成0x104C11DB7。把0x104C11DB7转换成二进制构成矩阵的第1行;然后把元素(2, 1), (3, 2), (4, 3), (5, 6), ··· , (32,31)置为1,形成一条斜线;其它元素为全0[17]。得到矩阵Ab,如图3所示。
1 bit的运算矩阵Ab乘8次方即得到8 bit的运算矩阵A1。通过Maxima工具,对矩阵Ab点乘8次后(矩阵乘8次方在Maxima中的运算符为^^8),再经过二值化处理,得到图4的运算矩阵:A1=Ab^^8。
最后,对A1矩阵求逆(矩阵求逆在Maxima中的运算符为^^-1),再经过二值化处理后,得到图5的逆运算矩阵:A1-1=A1^^-1。
至此,我们得到了8 bit的全0数据输入时的反运算矩阵。
然后根据反运算矩阵来实现回滚模块:
对回滚模块输出值CRC_rb(“rb”为rollback的简写)的每个bit,只要看矩阵A1-1对应的列(最左列对应bit31,最右列对应bit0)里哪些行不为0,将回滚模块输入CRC的对应bit(最上行对应bit31,最下行对应bit0)加到异或运算中即可。
用Verilog HDL代码表示为crc_rb[31]= crc[7]^ crc[6] ^ crc[4] ^ crc[2] ^ crc[0];crc_rb[30]=crc[6] ^ crc[5] ^ crc[3] ^ crc[1]; ···crc_rb[0] =crc[8] ^ crc[7] ^ crc[5] ^ crc[3] ^ crc[1]。
3 CRC算法的硬件实现
有了回滚运算逻辑模块,CRC运算硬件实现就比较简单了,逻辑框图如图6。
把末尾的无效输入字节都强制设置成0,这在设计上很容易实现。一般采用与门掩码处理的逻辑结构。
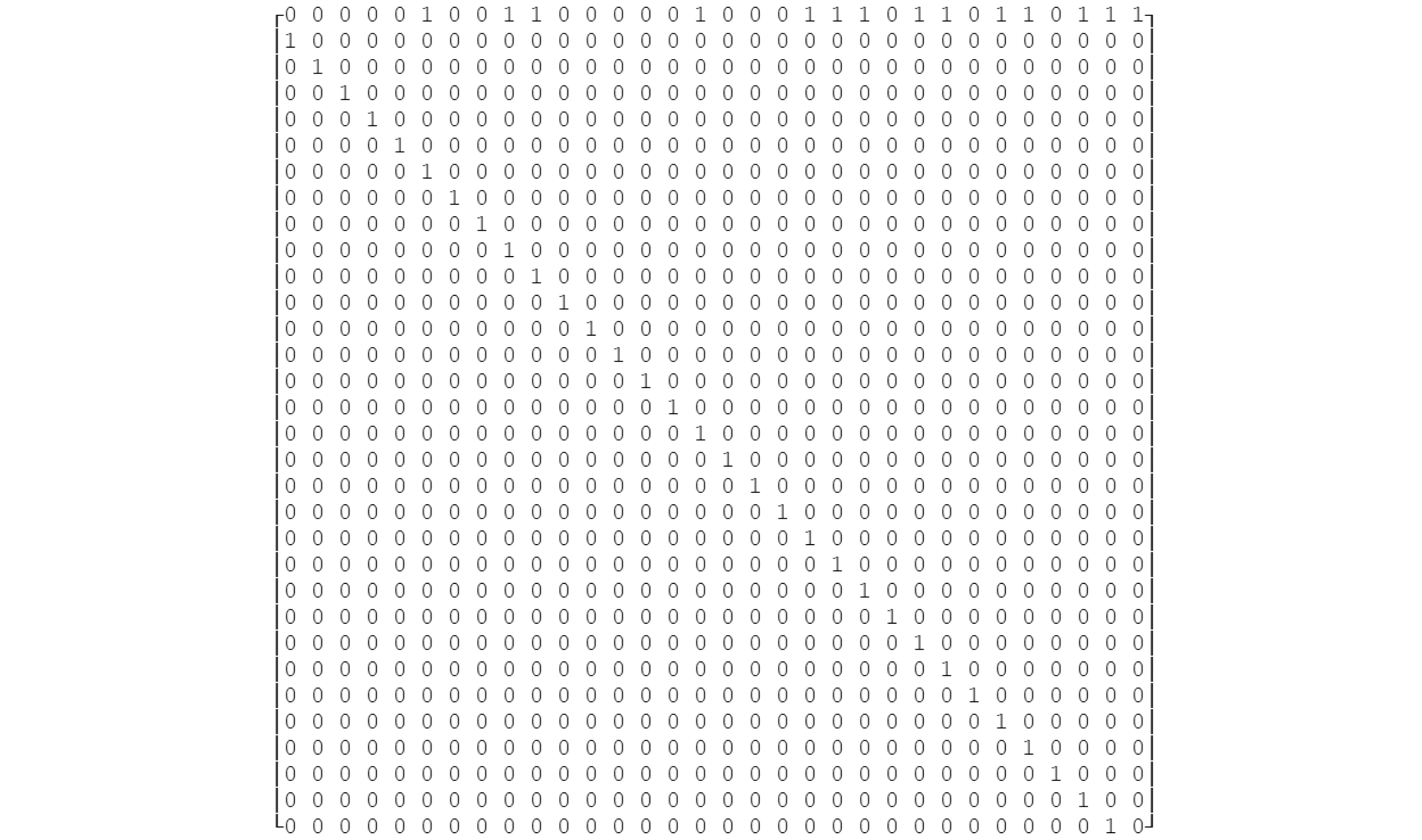
图3 1 bit运算矩阵
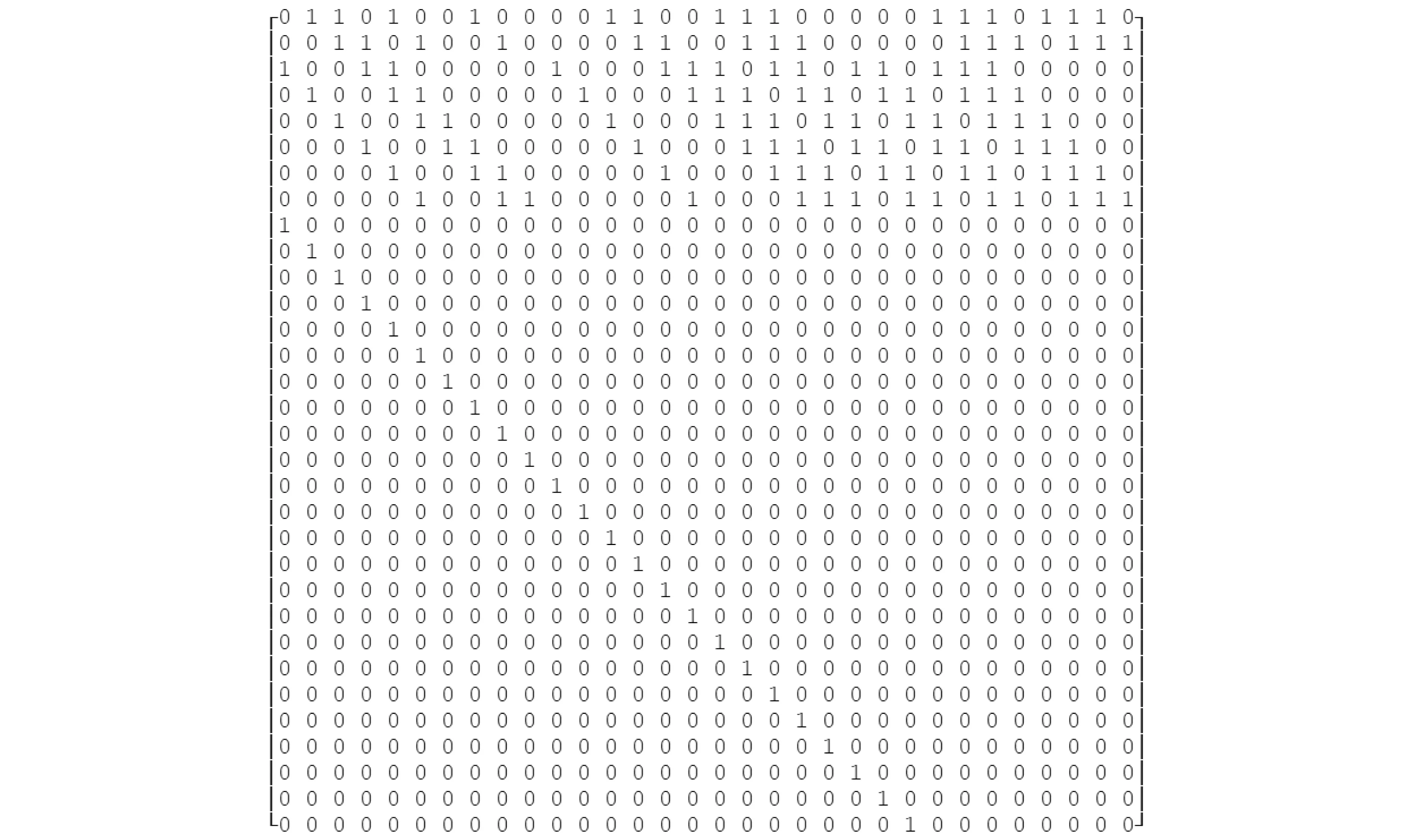
图4 8 bit运算矩阵
如果最后一个周期里,只有末尾1个字节是无效的,就把这个无效字节设置成0,然后依然按照完整的全位宽计算CRC,此时得到的结果就是CRC32E,即正确的结果CRC32C再多计算了一个全0的数据字节。
然后用这个CRC结果通过1 Byte回滚运算模块,进行回滚运算,最终得到的就是正确的CRC计算值。
如果末尾存在n个字节的无效数据,则需要重复回滚运算n次。在硬件实现上为了避免多次迭代操作影响处理速度,一般都会例化多个不同的回滚运算模块,每个回滚运算模块对应不同的回滚字节数。通过后再用选择器选择对应的回滚运算模块输出。

图5 8 bit逆运算矩阵

图6 硬件实现
这些不同回滚字节的回滚模块,其对应的矩阵也是不同的,可以用1 Byte反运算矩阵A1-1通过乘方的方式简单的算出来。
4 回滚算法的优势
以一个200 MHz主频,512 bit(64 Byte)的100 Gbit以太网设计为例,在传统设计实现中,其CRC运算需要使用64个不同输入位宽的模块,如图7所示。
对于一个64 Byte位宽输入的CRC运算模块;其输入数据为64 Byte的数据加上32 bit的上一次CRC结果,总共是544 bit输入,32 bit输出,运算逻辑是一个544×32的矩阵线性运算;一个63 Byte的运算模块的输入为536 bit,输出为32 bit,运算逻辑是一个536×32的矩阵线性运算;以此类推,最简单的1 Byte运算模块输入为40 bit,输出为32 bit,运算逻辑是一个40×32的矩阵线性运算。
回滚算法的CRC运算的构成如图8所示。
回滚式CRC算法里也包括了64个运算模块,包括1个64 Byte输入的CRC运算模块和63个回滚运算模块。其中64 Byte输入的CRC运算模块和常规CRC算法中的对应子模块相同,但回滚运算模块的就简单多了,每个回滚运算模块都是32 bit输入32 bit输出,运算逻辑为32×32的矩阵线性运算;和常规算法相比,比其中最简单的40×32的矩阵线性运算还简单。因此总体实现就更是简单得多。
5 实验数据
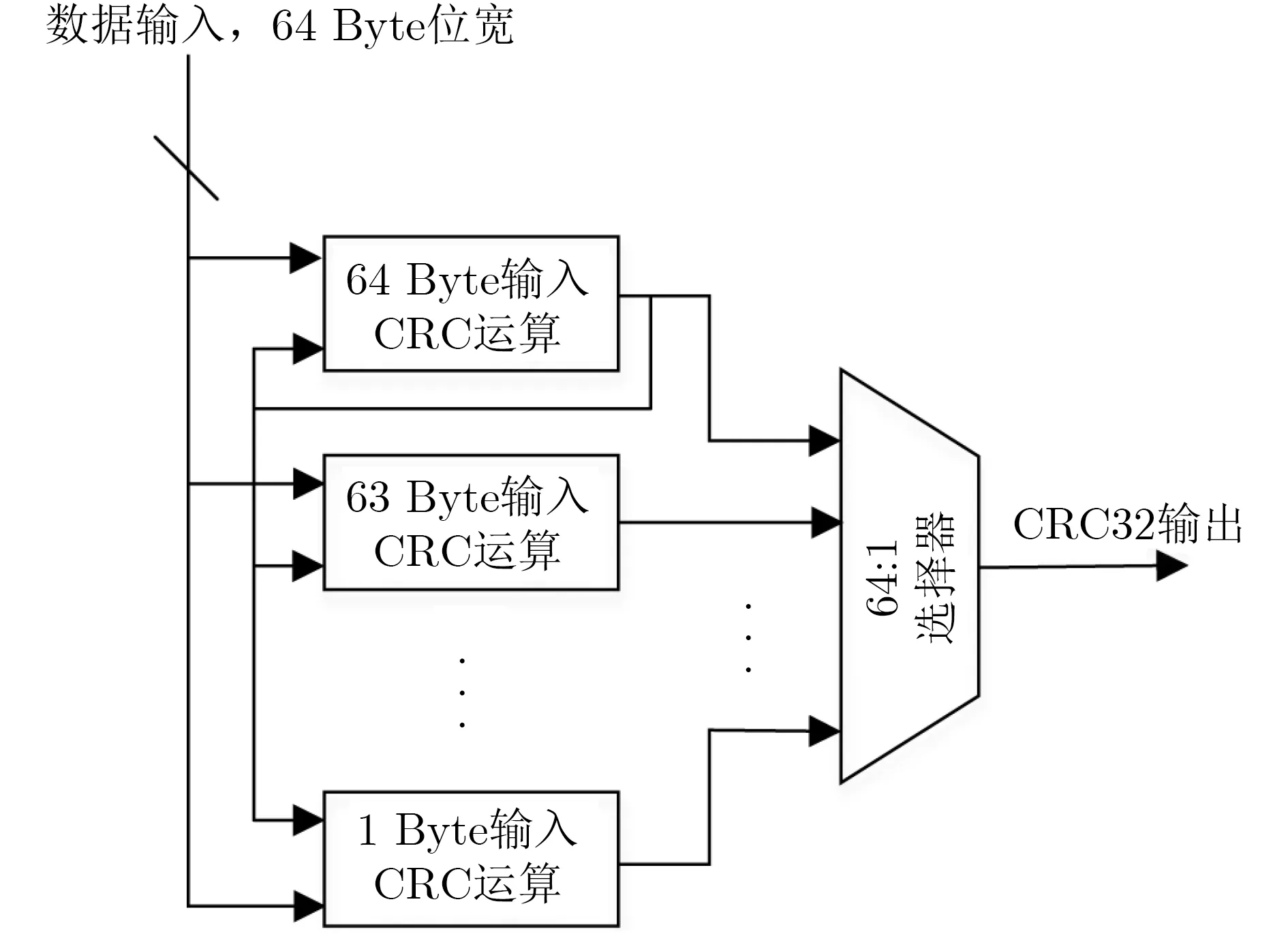
图7 传统实现方式

图8 回滚实现方式
以上一节的512 bit数据位宽输入,主频200 MHz的CRC32运算模块为实验对象,用完全相同的硬件/软件开发平台,在完全相同的FPGA器件上,实验传统算法和回滚算法两种不同的实现方式。
实验环境如表1所列。
对比两种算法下,资源占用情况和软件运行时间。得到的结果如下:
逻辑资源占用量,在Altera工具中以ALM(Adaptive Logic Module)数量为计量;逻辑综合耗时和布线耗时以秒为单位,两种算法的对比数据如表2所示。
可以看出,逻辑资源占用方面,回滚算法比传统算法节约了85%的ALM占用数量;在综合耗时和布局布线耗时方面,回滚算法比传统算法节约了60%~70%的时间,优势非常显著。
6 结论
针对传统的变位宽CRC算法中存在的不足,本文打破常规,从逆向思维的角度出发,通过逆运算的方式,从可控的错误数据中逆推出正确的数据。并利用矩阵运算的数学工具推导和实现了算法。
逆运算的CRC算法,也就是本文中说的回滚运算,在大数据位宽输入情况下,可以解决传统算法的臃肿低效问题。回滚算法在FPGA上通过了实验验证,实验不仅证明了回滚算法完全可行,而且可以显著地节约资源,降低复杂度。在512 bit位宽的情况下,回滚算法和传统算法相比,可以节约85%左右的ALM逻辑资源;节约70%的综合时间;节约60%的布局布线时间。体现出了巨大的优势。

表1 实验环境

表2 传统算法与回滚算法对比

