基于MCEEMD分解的多分支配电网行波测距
刘 畅,刘爱莲,李英娜,李 川
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.云南省计算机技术应用重点实验室,云南 昆明 650500)
0 引 言
配电网中各个分支线路区段长短不一。配电网发生故障时,技术人员需要尽快定位故障点的具体位置。故障精准测距主要通过分析区段内的故障信息查找故障点位置,是故障区段定位的下一步工作。找到故障发生区间后,需明确接地点位置。但是,仅靠人工查询费时费力。因此,需在准确定位故障发生区段的前提下对故障区段开展故障测距,从而找到接地点发生位置,具有较强的现实工程意义[1-2]。
近年来,国内外学者与研究人员对故障测距问题进行了大量研究与分析。目前,利用故障后信息进行测距的方法主要为行波法[3-8]。行波测距法可分为A型、B型、C型和D型4类。A型行波测距方法是根据行波波头首次抵达信息采集装置与故障点反射波抵达信息采集装置的时差为依据进行测距;B型行波测距方法是根据行波波头分别抵达区段两端信息采集装置的时差进行测距;C型和D型行波测距法是通过信号注入的方法完成测距。由于配电网分支线路繁多,拓扑结构复杂,系统内部反射波和折射波混乱、难以识别,A型行波测距法实行难度较大且精度较低。C型和D型行波法需要外加信号发射器,投资较大。B型双端行波测距法在故障区间准确识别的基础上,仅需利用区段两端测点获取行波信号,通过信号处理识别波头抵达两端的时间差即可完成故障测距,检测方便,容易实现,经济要求不高,且测距误差低。本文在故障区间内使用双端行波测距来精确定位故障点。
故障后的行波信号在阻抗不连续的地方存在反射和折射现象,因此故障行波具有较强的非平稳非线性特征。在信号分析过程中,希尔伯特-黄变换(Hilbert-Huang Transform,HHT)先对信号进行经验模态分解(Empirical Mode Decomposition,EMD),后采用希尔伯特变换(Hilbert Transform,HT)分析信号,对非平稳非线性信号的分析能力较强。本文采用HHT对信号进行时频分析,针对EMD分解存在的模态混淆问题,引入MCEEMD算法对行波信号进行分解。大量实验证明,所提方法在故障测距实验中的测距精度有所提高,且在T型支接线路下效果理想。
1 行波传输特性
1.1 行波原理
行波用于描述波的传输状态。当配电网系统发生接地故障时,由电路理论可知,故障点可以看作增加了一个虚拟电势,与故障发生前的电压大小相等但相位反向,导致故障点处的电压突变,从而产生向线路两侧传输的故障行波信号,如图1所示。行波信号包含了大量的故障信息,因此准确提取故障行波中隐藏的故障信息对故障测距意义重大。

图1 行波传输原理
1.2 行波的折反射原理
线路中经常存在波阻抗不连续点。如图2所示,A点为波阻抗不均匀点,左端波阻抗为Z1,右端波阻抗为Z2。行波在输电线路上传播时遇到该点会在此处发生折反射现象。行波折射波方向与入射波同向,反射波与入射波方向相反。折反射的存在避免了电压和电流幅值的突变。
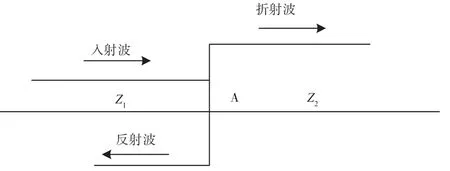
图2 行波折反射原理
电压行波的折、反射系数和电流行波的折、反射系数分别定义如下:
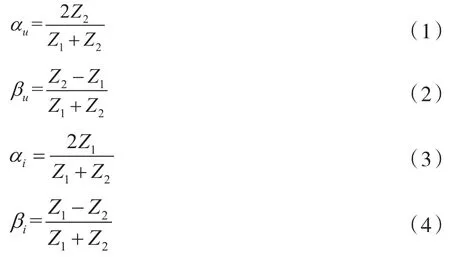
1.3 行波波速确定
工程试验表明,行波传播速度在频率为1 kHz时基本不会发生变化。而实际使用的行波定位装置采用的信号频率远比1 kHz高,因此行波传播速度是一个定值,不会对故障测距产生影响,可依据线路上的分布参数计算出行波速度。
行波波速计算公式为:

式中,L和C分别为各段线路的单位长度的分布电容与分布电感。
2 T型支接线路三端故障测距原理
本文故障精准测距采用双端波测距方法。为保障T型支接线路三端情况下的测距效果,根据双端行波定位方法原理,递推出可应用于T型支接线路区段的三端行波定位方法。
简单的T型支接线路如图3所示,O、P、Q分别为三端测点,A为T分支点,故障发生在A-Q分支上,F为故障位置。
使用单端行波测距方法时,由于O-A、P-A及Q-A的长度不尽相同,分别对O、P、Q三端使用单端测距方法虽然可以测出O-F、P-F及Q-F的距离,但无法确定故障发生在具体哪一个分支上。例如,对O点使用单端行波测距方法,当计算得到的故障距离LO-F´<LO-A(即故障位置在O-A分支上)时,可以得到准确的故障位置为O-A分支,且距离 O 测点距离为 LO-F´。但是,当 LO-F´>LO-A(即故障位置不在O-A分支上)时,无法确定故障位置是在P-A分支还是Q-A分支,导致结果不准确。
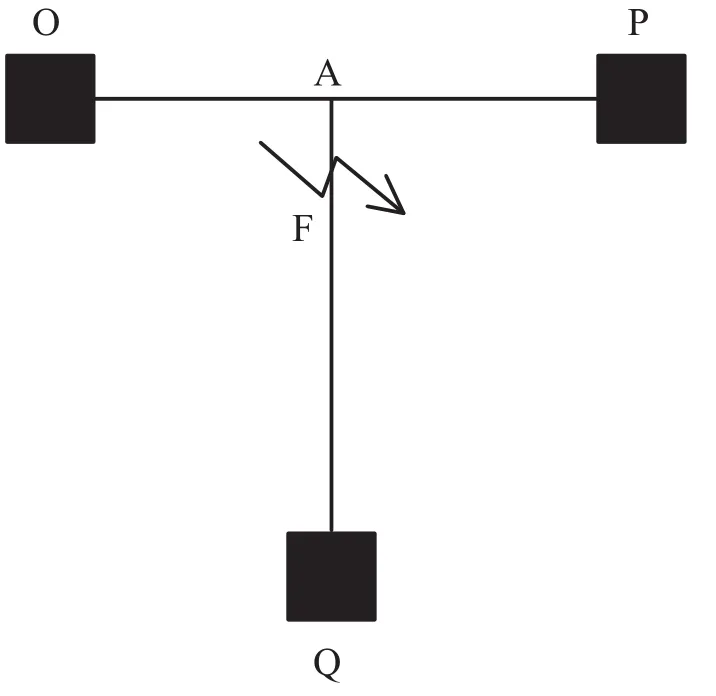
图3 简单的T型支接线路示意图
对O、P两端使用B型双端行波测距法时,F点产生的行波到达O点和P点的路径中A-F的距离是一定的。行波到达O点和P点的时间差的来源为OA和OP的距离差距,此时使用B型双端行波测距法计算故障位置,得到的故障点即为A点。不论F点位于A-Q分支上的哪个位置,对O、P两端使用B型双端行波测距法测到的故障位置都为A点,即产生了错误的测距结果。但是,这是T型支接线路下故障测距的一个特点,可巧妙利用这个特点使T型支接线路的故障测距方法变得简单。
由之前的分析可知,当T型支接线路区段发生单相接地故障时,对三分支中非故障分支的两个测点使用双端行波测距法会定位到分支点。因此,当故障区间在T型支接线路区间时,先任选两个测点进行双端行波测距得到故障位置F1,检测F1位置是否为分支点。此时,分两种情况讨论:
(1)F1不是分支点即F1点为故障发生点时,测距结束;
(2)F1是分支点,将所选的两个测点中的一个测点信息更换为第一次测距未选择的测点进行第二次双端行波测距得到故障位置F2,测距结束。
需要注意,由于各种因素导致的误差的存在,当计算结果得到F1点距离分支点较近时,也可以认为定位结果为分支点,之后进行第二次测距。当F1、F2计算结果同时为分支点或者分支点附近时,故障点即为分支点。
3 HHT变换
1988年,Huang[9]等人提出了经验模态分解(Empirical Mode Decomposition,EMD),并引入了Hilbert谱的概念和Hilbert谱分析的方法。美国国家航空和宇航局(National Aeronautics and Space Administration,NASA)以EMD和Hilbert transform提出者的姓名Hilbert-Huang Transform为这一信号分析方法定名,即希尔伯特-黄变换,简称HHT。
EMD分解是HHT变换较为重要的一步,将非稳定非线性的信号(基于时间变化)分解成本征模态信号(Intrinsic Mode Function,IMF),便于第二步采用HT变换将IMF信号转换为time-frequency的信号获得瞬时频谱,因此EMD分解的质量将影响HT变换的效果。
EMD算法自提出以来受到了学者们的喜爱。针对其存在的问题,学者们进行了大量改进。各种改进算法如表1所示。
故障后的行波信号在阻抗不连续的地方存在反射和折射现象,因此区段内的行波信号相当复杂。对于测点来讲,所监测到的故障信号存在较多的爆破点和突变点,会对分解效果产生影响。因此,本文引入改进的补充的总体平均经验模态分解(Modified Complementary Ensemble Empirical Mode Decomposition,MCEEMD)算法,对采集到的故障行波信号进行分解。MCEEMD算法是一种基于排列熵随机性检测的EMD分解算法。

表1 改进的EMD算法比较
3.1 排列熵
排列熵(Permutation Entropy,PE)是Bandt等设计的测定具体时间序列随机性和动力学突变的方案。它的基本原理较为简单,计算较为迅速,抗干扰指标相对较强。针对时间序列中的随机噪声,它可满足定量和定性分析的需求。尤其是对各类非线性数据,可以取得较为理想的分析效果,且有较为理想的鲁棒性,计算方式如下。
对实际长度数据为N的时间序列{X(i),i=1,2,3,…,N}开展相空间重构处理,可获得下述时间序列:

式中,m是嵌入维数,λ是时间延迟。
将 X(i)={x(i),x(i+λ),…,x(i+(m-1)λ)}的 m 个 量 按照升序重新排列,即:
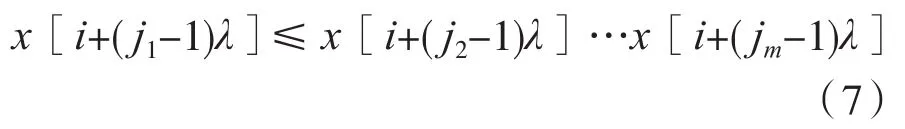
若存在 x[i+(ji1-1)λ]=x[i+(ji2-1)λ],则按 j的值的大小来进行排序,即当jk1<jk2,有:
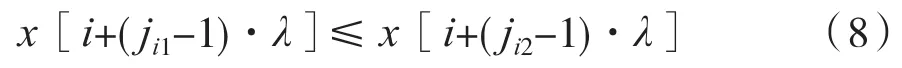
因此,任意X(i)都能够获得相应的符号序列:

式中,g=1,2,…,k,k≤m!。m个不同的符号{j1,j2,…,jm}共有m!种不同的排列,对应地共有m!种不同的符号序列,而S(g)只是m!种符号序列中的一种。计算每一种符号序列出现的概率
可以参考Shannon熵的具体形式将时间序列{X(i),i=1,2,3,…,N}的排列熵界定为:


Hp的实际取值区间为0≤Hp≤1,用于表述其中的随机状况。Hp参数相对偏大,代表其中的时间序列更加随机;反之,则代表其更加规则。
3.2 MCEEMD算法
对于非平稳信号S(t),MCEEMD方法的分解步骤如下。
(1)原始S(t)中,增添实际均值数据为零的白噪 ni(t)与 -ni(t),即:

式中,ni(t)为白噪,ai为幅值,i=1,2,…,Ne,Ne表示添加的白噪声对数。对开展EMD分解,可获得一阶IMF分量i=1,2,…,Ne。
(2)集成平均上述得到的分量:

(3)检查I1(t)是否为异常信号,若实际的信号熵值超过了θ0,认定其为异常信号,否则类似于平稳。
(4)若I1(t)被认定为异常,则继续执行步骤(1),直到IMF分量Ip(t)为非异常。
(5)将分解的前p-1个分量进行分离处理,即:
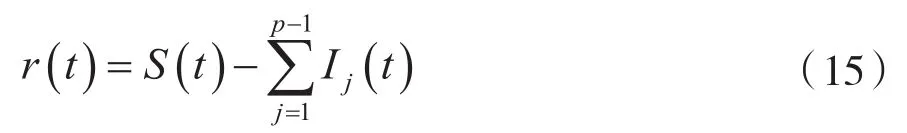
(6)针对剩余信号r(t)执行步骤(1)和步骤(2),分解获得的部分并不需要开展异常信号检测即可看作是IMF分量,可根据频率由高至低对其开展排列。
MCEEMD可减少EEMD和CEEMD中非必要的集成平均,不仅有助于分量具备相应的IMF意义,而且可减少EEMD与CEEMD的计算规模,避免重构误差,提升最终的完整程度。和EEMD、CEEMD类似,MCEEMD也要求选定白噪声的幅值ai和相关的增添对数Ne。由于当前缺乏严格依据,Wu[17]等将幅值定为标准差(Standard Deviation,SD)的0.1~0.2倍。集成次数以满足为宜,其中N为相应的集成次数,ε为添加白噪声的具体幅值数据,εn代表误差对应的最后标准偏差,是输入信号与获取的对应IMF分量和的差值。增添白噪声时,若实际的幅值数据过小,则无法转变实际的分布,无法产生均匀处理的效果。尽管增加实际集成次数可以控制影响,但会导致额外的运行时间。因此,ai的基本标准则是0.1~0.2SD,增添对数Ne通常在100以内即可满足要求。
4 仿真验证
为试验所提MCEEMD算法在行波分解中的效果以及所提行波测距方案的实际效果,使用Matlab/Simulink建立IEEE33节点系统进行验证,如图4所示。

图4 IEEE33节点配电网系统
4.1 MCEEMD分解效果验证
在线路8中通过Simulink中的Three-Phase Fault模块设置单相接地故障,并在S8测点提取故障行波信号开展EMD和MCEEMD分解,获得的分解结果如图5和图6所示。
由图5和图6可以看出,EMD分解获得的IMF有着显著的模态混叠。MCEEMD分解获得的IMF中并未出现模态混叠,且其中具体的分量频谱的相关突变点更加明确,只有参考多个尺度特征进行基本分解获得的4个本征模态,不存在其他异常信号,说明波形得到了准确分解。可见,MCEEMD在改善EMD算法存在的缺陷方面是有效的,可以完整、准确地提取信号信息,从而为后续故障定位提供方法。
4.2 测距效果仿真验证
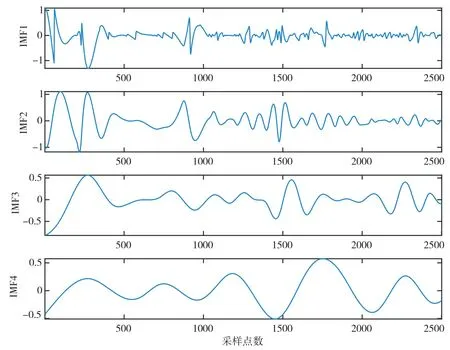
图5 EMD分解结果
通过Matlab/Simulink搭建IEEE33节点配电网系统,并结合改进的MEEMD算法的HHT分析进行故障测距效果仿真验证。建立的系统为中性点不接地系统,设定故障初相角为0°,故障接地电阻为0.1 Ω。为了方便描述,将T型支接线路分支点3点钟方向的分支称为α分支,6点钟方向分支称为β分支,9点钟方向分支成为γ分支。非T型支接线路的实验结果如表2所示,T型支接线路的实验结果如表3所示。

图6 MCEEMD分解结果

表2 实验结果(非T型支接线路)

表3 实验结果(T型支接线路)
5 结 语
本文介绍了配电网发生故障后的行波物理模型,对现有的行波测距方法进行了总结与分析,针对现阶段行波测距方案在T型支接线路上的空白,结合原有的行波测距理论,提出了一种适用于T型支接线路的测距方法。为了有效识别波头抵达时刻,分析传统HHT信息数据分析方法的优势和缺点,针对其EMD分解存在的端点效应和模态混叠现象,引进MCEEMD方法进行改进,并详细阐述了两种方法的基本理论、操作步骤及算法流程。使用Matlab/Simulink软件搭建仿真平台,结合基于MCEEMD算法的HHT的时频分析方法进行仿真验证。大量实验证明,所提方法在故障测距实验中测距精度较以往方法有所提高,并且在T型支接线路下效果理想。

