优选移动平均与BP网络混合电力负荷预测方法
何伟峰
(河南神马氯碱化工股份有限公司)
0 引言
电力行业事关国家经济发展和社会稳定,及时预测电力负荷对保障电力系统安全可靠、经济高效地运行十分重要。近年来,中长期电力负荷多以总体趋势预测为主,很少考虑数据的惯性增长、周期性变化和数值的积累误差,进而影响了负荷预测准确性,将基于此开展月度电力负荷预测的方法研究。
负荷预测方法根据历史负荷推导待预测负荷的方式可分为外推法和相关法,根据预测模型复杂度又可分为统计预测法与智能预测法。统计预测法包括回归分析法、时间序列法、指数平滑模型法、卡尔曼滤波法、状态估计法等;智能预测法包括人工神经网络法、模糊逻辑理论法、灰色理论法、支持向量机、极限学习机等。文献[1]提出一种从整体到节点,AR-ANN混合预测方法的研究。文献[2]通过总结负荷的周期性及节假日特性,并结合气象因素对电力系统负荷进行了短期的电力负荷预测。文献[3]利用移动平均法对数据采集进行平滑处理。文献[4]通过移动平均法对铁路客票销售量进行预测,结果表明预测结果与实际客流较吻合。文献[5]将负荷预测分为有功、无功两部分,就超短期多点负荷预测提出一种将等级与分区概念应用在自适应动态负荷模型中的新方法。文献[6]为提高基于神经网络负荷预测变量选取的和适度,将RS理论引入前期预处理步骤。文献[7]将多种机械学习算法与ARIMA方法复合,实现数据耦合修正。文献[8]说明一种从实际系统的试验分析中得到的响应分析方法。文献[9]将电力负荷进行年度和月度分解,把ARIMA方法融入BP神经网络。上述文献为提高电力系统负荷预测的准确性,对预测方法进行了各种改进。综合以上文献,本文针对我国某中部地区月度电力负荷建立电力负荷预测模型,提出一种优选平均移动和BP网络电力负荷的混合预测方法,经验证,此方法一定程度上提高了中长期电力负荷的预测精度,希望对电力系统中长期规划有一定的帮助。
1 理论基础
为分析某中部地区的电力负荷情况,研究电力负荷数据变化特性,采用一种基于优选移动平均法和基于BP神经网络的趋势性预测的综合预测模型,对月度负荷进行周期性预测工作,就两种方法在预测中的步骤做具体展开。
预测方法大体分为外推法和相关法,移动平均法是外推法,根据时间序列逐项推移,适用于即期预测,但本身模型有缺陷且无法容纳多源数据。BP人工神经网络法作为典型相关法,将待预测符合与历史负荷、历史气温等多源数据建立非线性关系进行预测,与相似月、网络参数、社会经济、政策密切相关。
1.1 优选移动平均法
移动平均法是一种有着广泛应用需求的预测技术,基本思想是:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法,可以用来消除周期变动和不规则变动,但因自身模型缺陷和移动次数、移动项数难以智能化确定,故对其模型和移动项做出优化改进。
1.1.1 移动平均预测模型的改进
对于时间序列{Xt},t=1,…,N,一次移动平均预测法是利用指标在过去n期的历史值Xt-n+1,…,Xt-1,Xt,构造移动平均序列1,…,N,以此来预测指标在下一期的未来取值但当时间序列呈单调走势时,一次移动平均模型会出现持续的正偏差或负偏差,故做改进如式(1)、式(2):
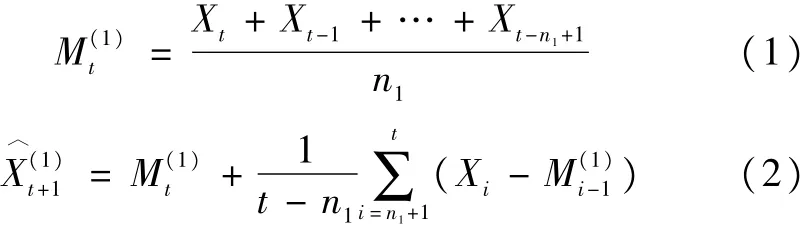
其中,n1为一次移动平均预测模型的移动项数,对于改进后的一次移动平均模型所得序列不仅给出预测值,而且加入了历史预测值与历史实际值之间的误差评估,一定程度上减少了预测偏差。
二次移动平均预测模型类似,采用模型如下:

其中,n2为二次移动平均预测模型的移动项数,同一次平均移动预测模型一样,加入了历史预测值与历史实际值之间误差评估的影响。
1.1.2 优选移动项数与移动次数首先,按照如下模型选择最优移动项数:
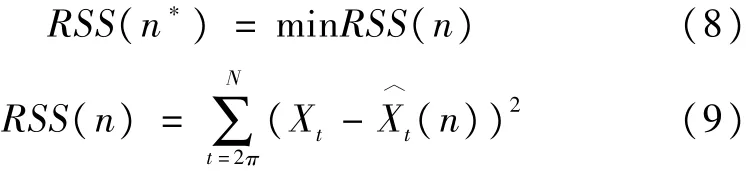
以能得到的最近n期预测值的移动项数为可行集,在可行集中遍历出所有移动项数,选择残差平方和最小的移动项数为实施一次移动平均预测的移动项数。
然后,按照如下模型确定最优移动次数:
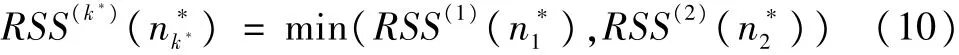
在最优一次模型和最优二次模型之间,继续根据最近几期残差平方和最小的原则确定最优移动次数。
1.2 BP人工神经网络
BP人工神经网络利用顺向传导过程所的输出值求得输出层校正误差,再将输出层误差经由隐含层逆向传导至输入层,循环往复直到训练稳定。可实现输入端与输出端非线性函数的函数映射问题,可以处理多源数据,覆盖中长期预测。
图1 为人工神经网络的网状式结构示意图,依次为输入层I、隐层J、输出层K。输入层I和隐层之间的线性关系为:

式(11)中,代表节点i的输出yi值;xij代表上层节点j的输出值;wij代表节点i与节点j的层间权值;f为激励函数,本文选择最常用的sigmoid激励函数,如式(12)

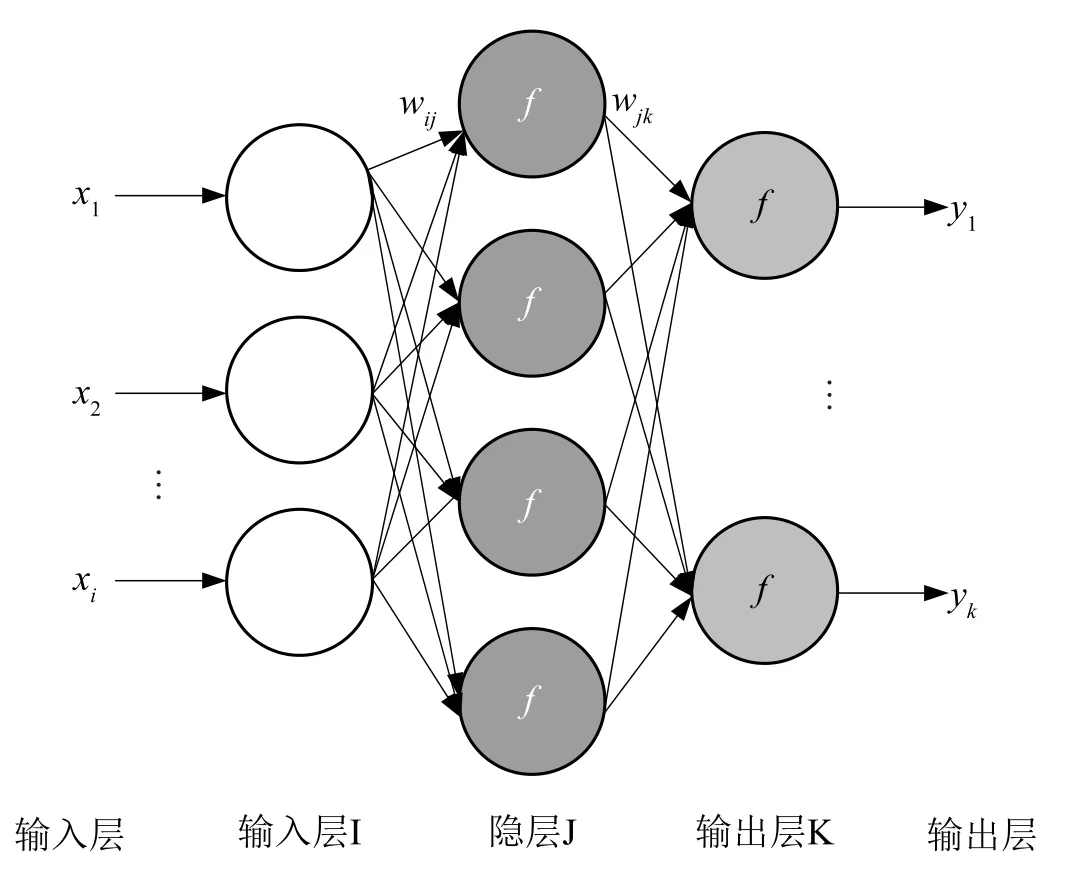
图1 BP人工神经网络结构图
2 模型构建
优选移动平均移动模型能够有效预测月度负荷,一定程度上降低了误差,但其模型无法容纳多源数据,二次移动平均模型会出现过拟合,难以直接用于月度负荷预测;BP人工神经网络可以处理多源数据、可以用于月度符合预测,但预测结果受历史数据、网络参数影响较大,因此,将优选移动平均法预测的结果用于人工神经网络的训练输入量,从而构成这种新混合算法,一定程度上提高了预测的准确性。
图2 是月度负荷预测基本流程图,整个预测流程可以分为数据输入、优选移动平均法初步预测、BP人工神经网络循环迭代、待测数据最终预测四个步骤,详细的预测步骤如下所示:
步骤1:对于月度负荷预测,根据前六个月负荷,使用优选移动平均法得到待测月负荷预测值,具体算法参考1.1。
步骤2:将优选移动平均法预测值加入构成一个月的样本,连通历史同月份其他数据(温度、风速)作为一组新训练样本点。经过BP人工神经网络运算完成负荷预测,BP人工神经网络算法参考1.2。
步骤3:记录预测数据,对比实际负荷,计算预测误差,分析数据。
3 仿真算例
3.1 实例数据
本文用电数据(月度用电量、接装容量、用户个数等)由某地区供电公司提供,地方宏观经济数据来源于统计局官网发布。分析以2010~2018年电力负荷为基准数据,对2019年1月份至2020年8月份电力负荷做出预测,对比实际用电量进行分析。
引入某区域企业特征,包括个数、运行容量等,数据见表1,为分析对比负荷预测准确率,引入2019.1~2020.8期间用电量变化情况,见表2。
3.2 数据分析
以预测2019年至2020年8月份的用电量为例,测试改进后的一次移动平均模型相比原始一次移动平均模型,预测能力的改善程度,如图3所示。
给定移动项数,n1=6,该图反映,改进后的一次平均预测值一定程度上减少了持续出现的负偏差,
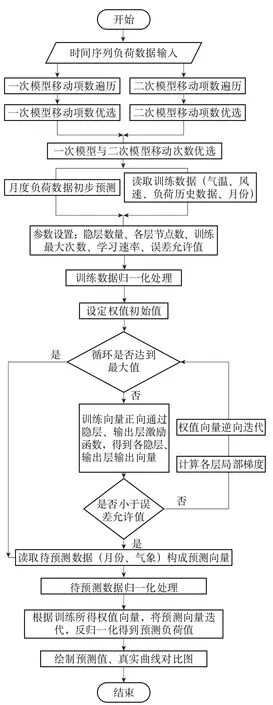
图2 负荷预测基本流程图
从而改善了预测能力,为下一步BP人工神经网络的训练参数奠定基础。

表1 大企业特征统计数据

表2 A、B、C三区用电量变化

图3 移动平均预测值改进前后对比图
将预测初始值及其他影响因素(历史值、温度、风速)因素经过筛选校核与历史月度负荷数据通过BP神经网络预测模型进行多因素耦合预测,该模型为基于影响因素及负荷序列数据趋势性发展的周期性预测,其神经网络模型参数如表3所示。

表3 BP模型参数
算法模型采用2010~2018年间月度符合数据进行学习,预测2019年至2020年8月月度负荷数据,对比2019年至2020年8月月度负荷数据,真实值与混合法预测值吻合程度较好,预测及对比如图4所示。

图4 多种预测负荷值与实际负荷对比图
预测的用电量总体呈增长趋势,但增长速度由于疫情影响对比前几年有所放缓。为体现混合预测方法的预测优势,将这几种方法模型误差进行对比,计算模型的MAPE值,如表4所示。

表4 MAPE值比较
可见混合方法误差MAPE指标为2.1%,和前三种预测方法比较,具有明显的预测优势,混合方法预测精度较高,适用于月度负荷预测。
从用电量趋势来看,疫情在2020年1、2月份对电力负荷冲击最大,低于往年电力负荷,预测值有所偏差,应用优选平均法的初值后,混合算法的预测值精度得到一定的提高。随着企业复工复产,2020年8月同期用电量超过2019年同期数据,生产经营活动迅速恢复,在不考虑其他因素的情况下,预测9~12月,区域月度电量按季度趋势变化将有所下滑,相比上年有所增长,但增长速度有所减缓。
4 结束语
经济发展与产业用电方面,用电量表现和宏观经济走势较为一致。本文提出了一种新型的混合预测模型,将优选平均移动法与BP网络相结合,模型加入了历史预测值与历史实际值之间误差评估的影响,克服了一次预测模型持续出现的正偏差或负偏差,提出优选移动项数和移动次数的方法,能够同时兼顾趋势性、周期性并综合温度、风速电力负荷影响因素耦合增加预测精度,可为中长期月度负荷预测提供更符合事实依据的负荷预测方法。

