基于MATLAB and Simulink的波浪能装置液压能量转换系统仿真研究

叶 寅，盛松伟，乐婉贞，王坤林，张亚群

（1.中国科学院广州能源研究所，广东 广州 510640；2.中国科学院可再生能源重点实验室，广东 广州 510640；3.南方海洋科学与工程广东省实验室（广州），广东 广州 511458；4.广东省新能源和可再生能源研究开发与应用重点实验室，广东 广州 510640）

波浪能作为一种可再生能源，具有储量丰富、分布广泛等特点[1]，并且在转换过程几乎不产生污染，因此受到越来越多的沿海国家重视，如何开发和利用波浪能成为了当前研究热点。

波浪能最主要的利用方式就是发电，波浪能装置一般通过三级能量转换过程，将波浪能最终转换为电能[2]。第一级是将波浪能转换为机械能，第二级将机械能转换为压力能或其他形式的能量，第三级将压力能转换为电能。第一级能量转换系统又称为能量俘获系统，二、三级转换合在一起称为能量转换系统。根据能量转换系统的不同可以将波浪能装置分为气动式、水力透平式、机械式和液压式等[3]。由于波浪的方向和大小都是随机的，且具有低频、出力大等特性[4]，而带有蓄能环节的液压系统可以很好地缓冲由于波浪的这些特性带来的冲击，使最终的能量输出平稳，达到并网的要求。因此液压式的能量转换系统成为当前波浪能装置能量转换方式的主流选择，国际上比较著名的波浪能装置如 Pelamis[5]、Wavestar[6]、Powerbouy[7]以及中国的“鹰式”系列波浪能装置[8]都是选择液压转换系统作为能量转换方式。

目前，国内外对于波浪能装置的研究主要集中在能量俘获过程中装置的水动力学部分，对于能量转换部分的研究较少，在实海况下装置的能量转换系统的数据更为稀少。针对以上情况，本文对具有蓄能环节并且设有液压自治控制器的波浪能能量转换系统进行了仿真研究，同时利用实海况条件下的能量转换系统试验数据作为比对，验证仿真模型的准确性。并模拟了在不同波浪条件下，液压能量转换系统的发电特性。本文的液压式能量转换系统仿真研究可以为实型波浪能装置能量转换系统的参数设计提供理论依据，为预测波浪能装置发电功率提供参考。

1 液压式能量转换系统原理

波浪能装置液压发电原理如图1所示。在波浪的作用下，吸波浮子随波浪往复运动，连接在浮子上的液压缸5做相同频率的上下往复运动，液压缸在往复运动的过程中，将液压油从油箱12泵入到蓄能器组6中，当液压缸往上运动，液压缸有杆腔将液压油经过单向阀2泵入蓄能器，液压缸无杆腔通过单向阀3将液压油吸入，当液压缸往下运动时，无杆腔的液压油通过单向阀4进入蓄能器组6。与此同时，有杆腔通过单向阀1从油箱12吸入液压油。因此在液压缸不断的往复运动过程中，液压油通过液压缸不断的被泵入蓄能器，蓄能器随着液压油的不断增多，压力逐渐上升，此过程将液压缸的机械能转变成了液压油的压力能存储于蓄能器，实现了短期的能量蓄积。当蓄能器的压力上升至设定值时，通过一定的逻辑控制方案，将液动换向阀9打开，蓄能器中的液压油进行释放，冲击液压马达10，液压马达带动发电机11旋转，将液压能转换为电能。波浪比较小的情况下，由于液压缸的运动速度比较慢，由液压缸泵入蓄能器组的液压油流量小于液压马达的流量时，蓄能器的压力会下降，下降到设定的关闭压力值时，通过控制液动阀，使液压马达和发电机停止旋转，蓄能器组又开始下一个蓄能过程。如果波浪比较大，使液压缸运动速度加快，由液压缸进入蓄能器的流量大于液压马达的流量，进入蓄能器的液压油多于流出的，蓄能器的压力会继续上升，直至相等，此时液压马达转速基本稳定，系统连续发电。

为了实现上述控制方案，本文采用液压自治控制器，如图1中的元件8。液压自制控制器主要由控制液压缸13，蓄能器16，以及球阀14和15组成。液压自治控制器的原理如下：当蓄能器组6的压力增大时，控制液压缸13左移，首先关闭球阀15（初始状态是开启），控制液压缸13左腔的油逐渐进入蓄能器16，随着蓄能器组6的压力继续增大，控制液压缸13继续左移，打开球阀14（初始状态是关闭），此时控制油路可以通过14进入到液动换向阀阀9，液动换向阀9打开，液压马达开始工作；当蓄能器组6的压力下降时，蓄能器16的液压油会回到控制液压缸13的左端，控制液压缸13右移，关闭球阀14，液动换向阀9的控制油口仍有油，液动换向阀9仍处于打开状态，随着蓄能器组6的压力继续下降，控制液压缸13继续右移，直至打开球阀15，液动换向阀9控制油口的油通过球阀15流向油箱，液动换向阀9回复原位，液压马达关闭。

图1 液压能量转换系统原理图

2 系统数学模型

通过系统图1可以看出，系统主要包括液压缸、单向阀组、蓄能器、液压自治控制器、马达和发电机组。本文分别建立各个液压元件的数学模型。

设液压缸的运动速度为v，每次运动行程h，缸径d1，液压杆直径d2，经过单向阀1吸油并通过单向阀2进入蓄能器的有杆腔流量Q1和经过单向阀3并通过单向阀4的无杆腔流量Q2分别表示为：

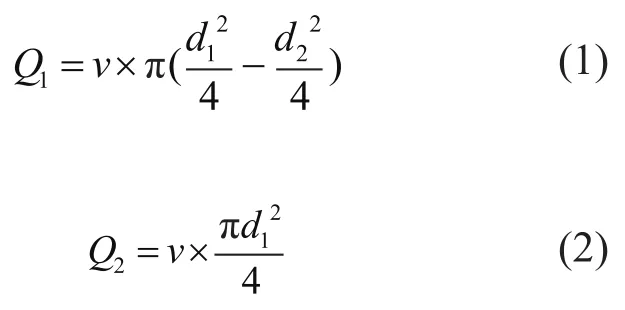
蓄能器采用皮囊式，如果蓄能器入口的流体压力比皮囊内气体的压力高，则流体进入蓄能器并压缩气体，从而储存能量。在整个发电过程中蓄能器经历了两个过程，一个是充油过程（气体压缩过程），一个是放油过程（气体膨胀过程）。蓄能器皮囊内气体的热力学过程可以表示为:

式中：pa为蓄能器压力；Va为体积；γ为气体常数。

设蓄能器的初始压力为ppr，蓄能器的皮囊内气体初始容积为Vpr，蓄能器中液压油的容积VF和流量QF的表达式如下：

塑料件主壁厚的大小取决于产品需要承受的外力、是否作为其他零件的支撑、承接柱位的数量、伸出部份的多少以及选用的塑胶材料而定。从经济角度来看，过厚的产品不但增加物料成本，同时也延长生产周期,增加生产成本。从产品设计角度来看，过厚的产品增加引致产生凹痕或气孔等不良缺陷，大大削弱产品的刚性及强度。本研究主壁厚值分别采用：1.5、1.6、1.8、1.9、2.0、2.2、2.5、3.0 mm，其他条件保持不变，分析主壁厚变化对塑料件翘曲变形的影响。

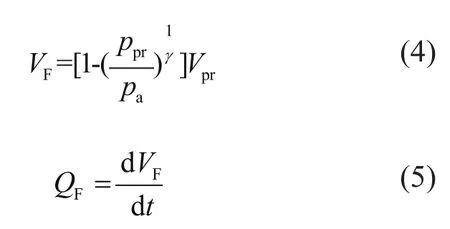
由液压缸、蓄能器和马达的连续性方程可得[9]：

式中：E为油液体积模量；Qm为马达的流量。

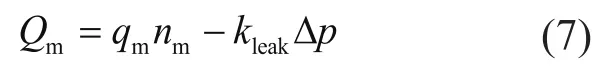
式中：qm为马达排量；nm为马达转速；kleak为马达泄露系数；Δp表示液压马达的进出口压差，该值通过液压自治控制器来控制，设定液压自治控制器的开启压力为popen，关闭压力为pclose。当蓄能器压力pa＞popen，Δp=pa。当pclose＜pa＜popen时，会出现两种情况，第一种是蓄能器处于充油过程（气体压缩过程），Δp=0；第二种是蓄能器处于放油过程（气体膨胀过程），Δp=pa。马达输出转矩Tm为：

式中：ηm为液压马达机械效率。

液压马达和永磁发电机的转矩平衡方程为：

式中：J为马达转动惯量，单位kg·m2；ωm为马达转动角速度；Bm为马达轴上的粘性阻尼系数；Tf为轴系静摩擦力矩；Te为永磁同步发电机的转矩。

三相永磁同步发电机，选择三相正弦模型，假设电机铁芯的导磁系数恒定不变，三相绕组完全对称，永磁体产生的磁场沿气隙周围正弦分布。得到永磁同步发电机的电气模型为[10]：

式中：ψd和ψq可以表示为：

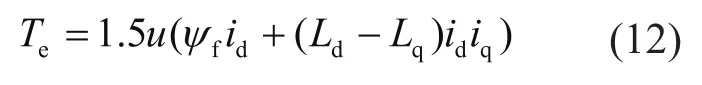
式（10）～式（12）中：ud和uq分别为d轴和q轴的电压；ψd和ψq以及ψf分别为d轴和q轴以及转子的磁通量幅值；id和iq分别为d轴和q轴电流；Rr为发电机定子线圈绕组的电阻；ωe为发电机角速度。发电机的线电压为：

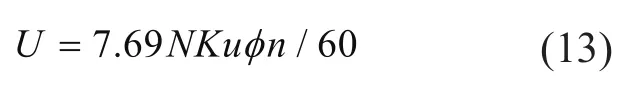
对于电阻负载模型，永磁同步发电机所接的负载为电阻负载，阻值为R，发电机功率可以表示为：

3 MATLAB and Simulink仿真模型

根据第2节中所建立的数学模型，利用MATLAB and Simulink软件对波浪能装置液压转换系统进行仿真实验。首先建立系统的仿真框图，根据系统的特点和MATLAB and Simulink液压仿真软件的特性，将液压转换系统分成3个子模型，分别是液压子模型、控制子模型、发电子模型。液压蓄能子模型包括液压缸、单向阀组和蓄能器组和液压马达等，建立的仿真框图如图2所示。

图2 液压子模型MATLAB and Simulink模型框图

对于控制子模型，当蓄能器组压力达到设定的开启值时，主油路的液动阀打开，马达开始发电，当蓄能器压力降至设定的关闭值时，液动阀关闭，马达也随之关闭。控制系统都是由液压元件组成，没有电力电子元件，减少控制器在恶劣海洋环境下的故障，确保系统可以稳定的工作，这部分与其他采用液压式转换系统的波浪能装置有所不同，控制子模型的MATLAB and Simulink框图如图3所示。

发电子模型包括永磁同步发电机和负载，MATLAB and Simulink模型如图4所示。将建好的液压、控制和发电子模型连接，得到能量转换系统的模型框图，设定仿真时间及相关参数，进行仿真。

图3 控制子模型MATLAB and Simulink模型框图

图4 发电子模型MATLAB and Simulink模型框图

4 实海况系统和仿真结果对比

为了验证仿真的效果，将仿真数据和波浪能装置实海况实验所得数据进行比较。设置实验参数如下，蓄能器容量为500 L，设置液压自治控制器启动压力为16 MPa，关闭压力为9 MPa，负载电阻为6 Ω，液压马达排量为107 mL/r，额定转速1 500 r/min，发电机额定电压400 V。仿真时液压马达容积效率取93%，总效率取90%[11]。

得到的实海况实验结果和仿真结果如图5至图7所示。图5是实验得到和仿真得到的发电机功率曲线，两条曲线基本重合，实海况实验的发电平均功率为17.658 kW，仿真的平均功率为19.46 kW，二者之间的相对误差为9.26%。图6所显示的是液压马达的流量曲线，实验得到的平均流量为0.002 21 m3/s，仿真得到的平均流量为0.002 163 m3/s，实验和仿真的相对误差为2.12%。图7所示的是发电机电压的曲线，实验所测的电压平均值为320.69 V，仿真的电压平均值为337.71 V，电压的相对误差为5.03%。

图5 实验和仿真得到的功率曲线

图6 实验和仿真得到的流量曲线

图7 实验和仿真得到的电压曲线

通过得到的发电功率、液压马达流量以及蓄能器的压力等数据，通过液压发电端的效率公式（15）可以计算液压系统的转换效率。式中：Pi为录得功率数据；Δt1,i为两个功率数据之间时间步长；Q,i和pa,i分别为录得的流量和功率数据；Δt1,2为录得流量和压力数据的时间步长。

通过计算得到，实型波浪能装置液压系统实验液压到电的效率为69.29%，模拟仿真得到的液压到电的效率为76%。

5 规则波和随机波下仿真及结果分析

为了研究不同波浪条件下液压能量转换系统的发电特性。本文分别做了随机波和规则波下的能量转换系统仿真。为了缩短仿真时间，修改了第4节的仿真参数，将蓄能器的容量改为100 L，液压马达排量改为65 mL/r，阻值改为8 Ω。给液压缸端施加两组不同的输入信号来模拟波浪，一组是不规则的随机速度信号，模拟不规则波浪，如图8所示，另一组是规则的正弦信号，模拟规则波，如图9所示。

图8 随机速度信号

图9 正弦速度信号

仿真时间为100 s，得到液压缸有杆腔和无杆腔的流量如图10和图11所示，通过液压缸的流量曲线可以看出，液压缸的流量基本和输入的信号相一致。

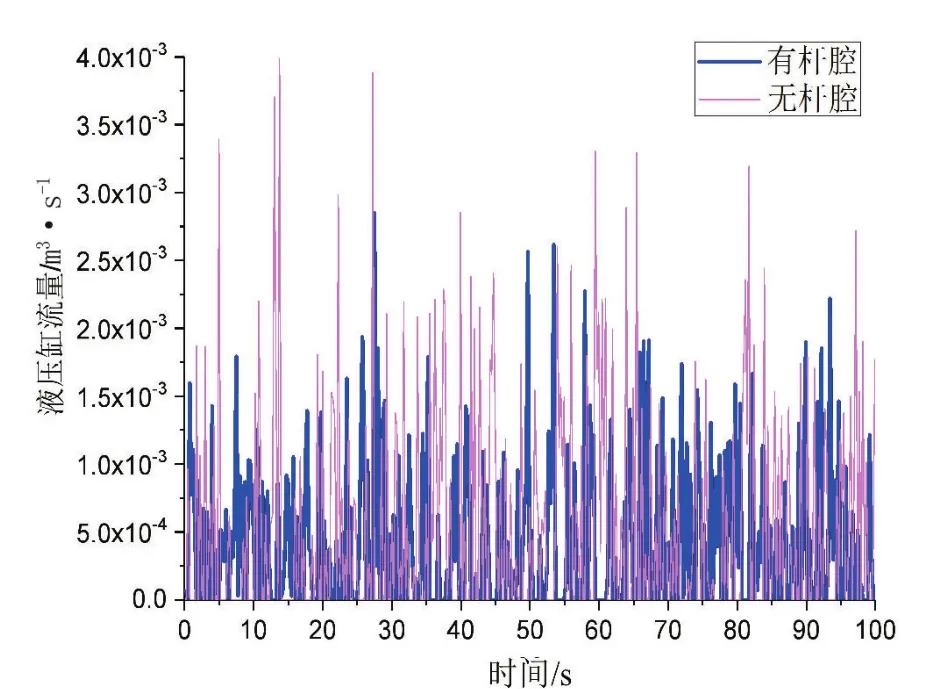
图10 随机信号下的液压缸流量

图11 正弦信号下的液压缸流量

图12所示的是蓄能器中的压力pa在两种不同的输入信号下的变化曲线，从图12可以看出，经过蓄能稳压之后，两组工况下蓄能器的压力值都在所设定的启动压力popen和关闭压力pclose之间波动。

图13至图15所示的是两组工况下发电特性曲线图，分别为功率，转速和电压。从图13得到，两组信号下最大的发电功率值约为26.6 kW，最小发电功率为约为8.88k W，并且两个工况下在系统进行发电时功率、马达转速和发电电压曲线基本平行，曲线的趋势和走向也基本一致，说明经过蓄能稳压之后，系统的发电功率与输入的信号已经基本没有什么关联性。

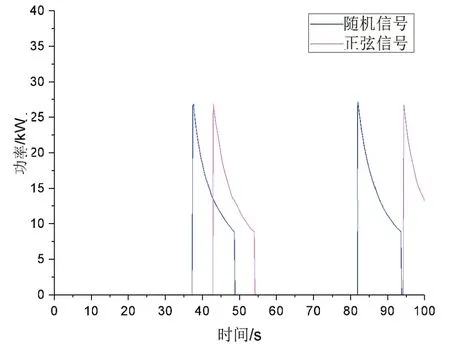
图13 两组工况下发电功率

图14 两组工况下液压马达转速

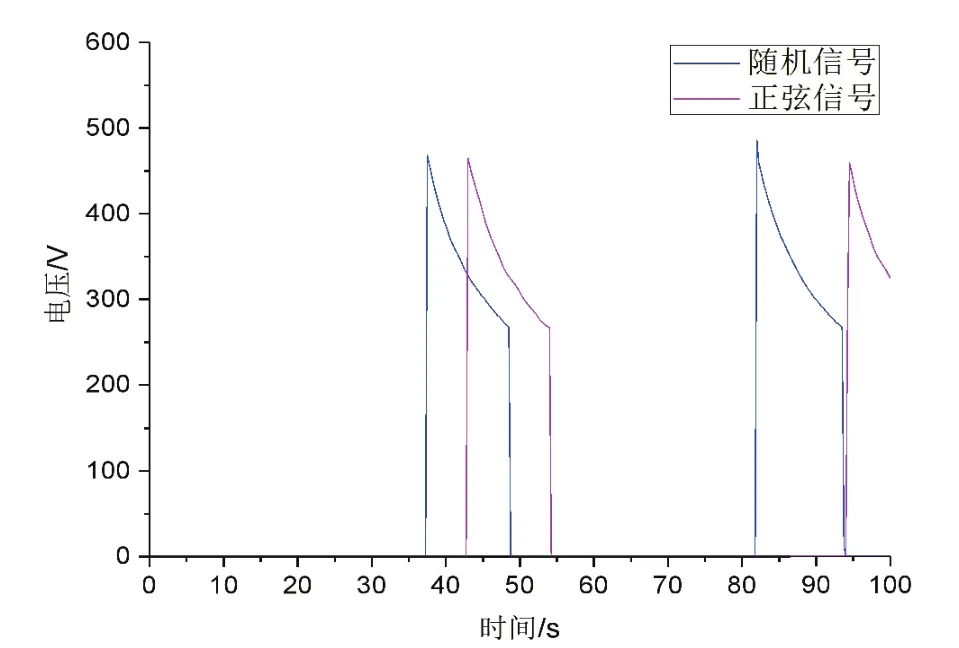
图15 两组工况下发电机电压

6 结 论

本文研究了带有蓄能环节和液压自治控制器的波浪能装置液压能量转换系统，通过对系统的建模仿真研究，得到以下研究结论：（1）将波浪能装置实海况实验与仿真结果对比，二者得到液压能量转换系统的发电特性（包括发电功率、液压马达的流量和发电机电压）基本一致，实验和仿真的相对误差分别为9.26%、2.12%和5.03%。此外通过计算得到了实验和仿真的液压到电的效率分别为69.29%和76%，验证了本文仿真模型的准确性；（2）通过模拟不同的波浪信号输入，经过液压能量转换系统，在启动压力和关闭压力设定的情况下，模拟随机波和规则波输入得到的发电特性基本相似，意味着通过本文所设计的液压能量转换系统，可以将不稳定的波浪能转换成稳定的电能，最终输出的电力特性曲线与输入的波浪特性关联性已经不大，输出的功率和电压比较稳定，提高了发电质量，从而使发电机后端的电力变换更为方便。