基于Matlab 求解时谐复系数弹性波方程的超弱变分方法1)

袁 龙 赵茂先

(山东科技大学数学与系统科学学院，山东青岛266590)

“偏微分方程数值解” 课程是数学与应用数学、信息与计算科学等专业的核心课程。该课程针对刻画物理模型的数学方程，利用有限元、有限差分法、有限体积法和边界元法等方法数值求解方程，并理论分析相应数值解的误差收敛阶。该课程涉及知识面广泛，不但要讲授变分方法、索伯列夫空间、离散空间(如多项式空间)、线性方程组的迭代求解及数值逼近，还要培养学生的编程验证能力[1-3]。因此，学生系统地掌握该课程的知识结构是至关重要的。

本文基于间断有限元方法数值求解描述一大类物理问题模型(比如声波散射、弹性波散射问题) 的弹性波方程。在数值求解弹性波方程的发展过程中，有限元[4-5]、边界元法[6-7]和有限差分方法[8-9]起到了很重要的作用。弹性波方程解析解的一个重要参数是波数。它描述了解析解的振荡行为。波数越大，振荡越频繁。这个特点在有限元分析中可以通过经验法则来刻画——单个波长内的网格点数。因而由此经验法则很难获得大波数情形下令人满意的数值结果。为了克服此缺点，很多改进方法[10-12]被陆续提出。最近用来求解中高频弹性波方程的平面波方法[13-15]在工业界和数学界比较流行。平面波方法的核心是选取满足无约束方程的精确解作为逼近基函数，如平面波函数、贝塞尔函数、格林函数等，并且未知量是定义在剖分单元上的。大量的数值实验表明，相比其他离散化方法，在满足相同精度的条件下，平面波方法使用了相对较少的自由度；即，在选取相同自由度的条件下，平面波离散化方法具有较高的精度。

为了让学生直观感受平面波方法数值求解偏微分方程的过程，本文从方程组本身出发，分别构造满足弹性波方程和其对偶方程的测试函数空间和检验函数空间，并基于间断有限元思想，结合分部积分公式，推导出复波数情形的超弱变分形式；分别构造二维空间下的平面波检验离散函数空间和测试离散函数空间，进一步得到等价的变分形式。数值实验验证了新方法的数值解具有较高的精度。

1 控制方程与数值方法

1.1 弹性波方程

考虑边值问题[16]

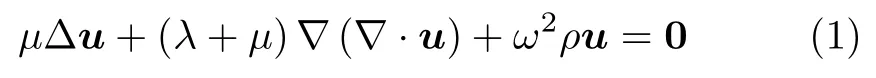
及最低阶吸收边界条件

其中，拉梅常数λ和µ借助于泊松比ν和杨氏模量E表达

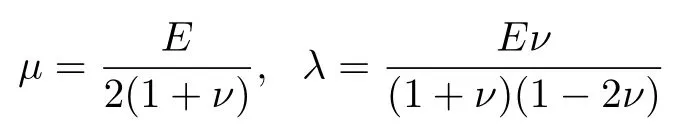
材料密度ρ>0 是常数，ω >0 是角频率，n是边界的单位外法向，i 是虚部单位，截断算子Tn(u) 为

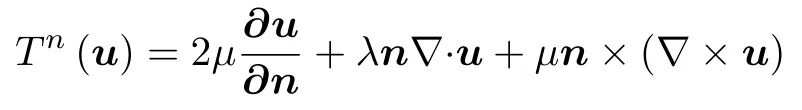
定义纵波和横波的波速分别为

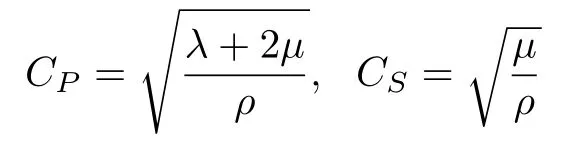
定义在边界上的正定矩阵σ为

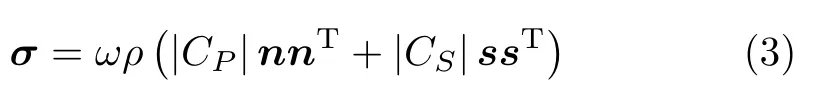
其中s是边界的单位切向量，|CP|与|CS|分别表示CP与CS的模，·T代表·的转置。假定求解区域Ω是有界多面体区域。Th表示区域Ω的三角剖分并满足“形正则”和“拟一致”假设[17]。定义为简单起见，我们只考虑二维区域模型，但方法可以直接推广到三维空间。

1.2 弹性波方程的变分形式

对于每一个剖分单元Ωk，令H1(Ωk) 为标准的向量索伯列夫空间，并定义分片间断Trefftz 变分空间[18]

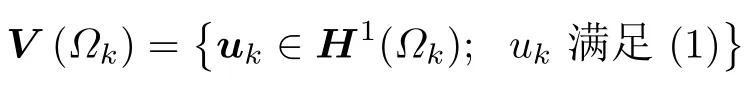
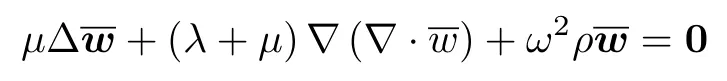
和区域间断Trefftz 测试空间

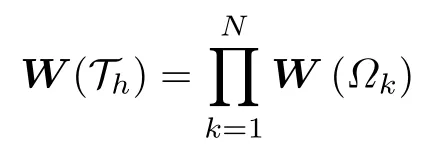
对于每个单元Ωk，定义迹算子

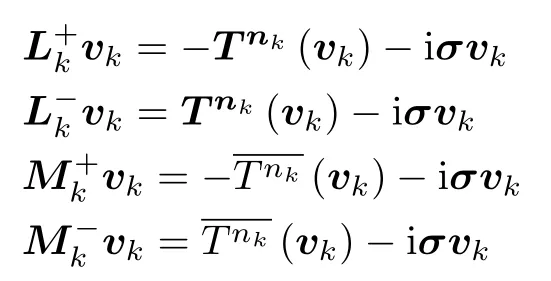
利用等距引理[19-20]，原问题(1)(2)等价于变分形式：寻找u ∈V(Th) 满足

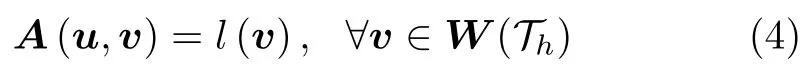
其中半双线性型

右端项为

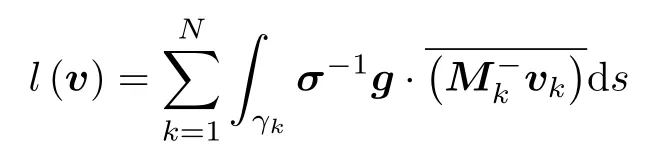
1.3 平面波离散化

本节构造间断 Trefftz 变分空间V(Th) 的平面波离散空间Vp(Th)。首先考虑沿单位方向d传播的时谐弹性平面波，其可分解为纵波与横波之和

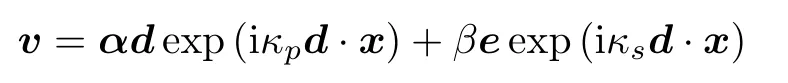
其中κp=ω/Cp,κs=ω/Cs，α,β是系数，d ·e= 0。纵波vp=αdexp(iκpd·x) 和横波vs=βeexp(iκsd·x)。简单计算可知，纵波和横波均满足原始方程 (1)，且∇×vp= 0,∇·vs= 0。理论分析和实际应用表明，借助于选取单位圆周上分布均匀的一簇互不相同的弹性波传播方向

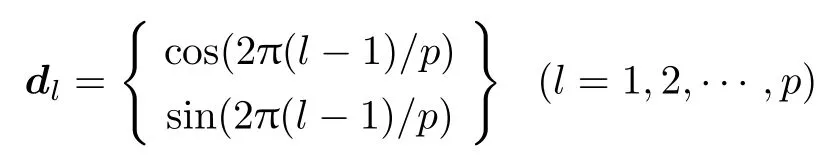
我们得到定义在每个单元Ωk上的2p个复平面波基函数

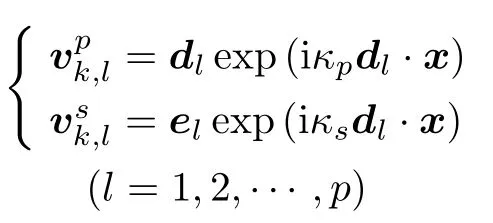
记Qq(q= 2p) 表示单元Ωk上的上述 2p个复平面波基函数张成的空间，则平面波离散空间Vp(Th) 为

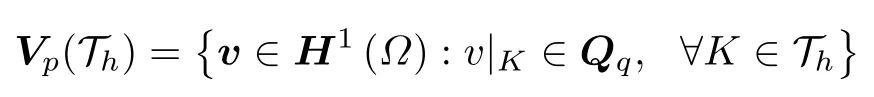
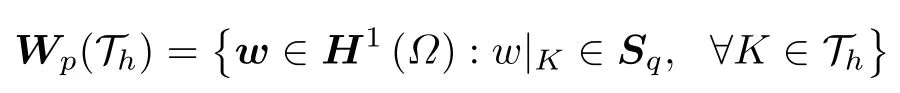
定义解析解uk=u|Ωk的平面波逼近uh,k

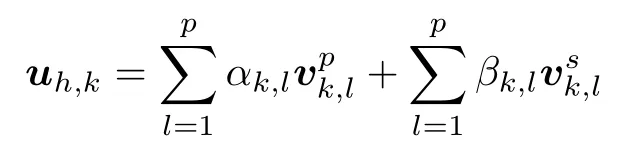
其中αk,l,βk,l(k=1,2,··· ,N;l=1,2,··· ,p) 为待求解的系数。对应于连续变分形式(4) 的离散形式为：寻找uh ∈Vp(Th) 满足

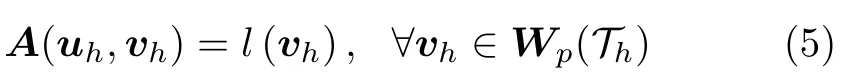
我们利用直接法，即高斯消去法[21]，求解上述离散线性方程组。

1.4 算法实现

步骤 1. 初始化输入参数：计算区域Ω,λ,µ,ω,ρ,σ；

步骤2. 剖分区域Ω形成三角网格Th；

步骤3. 基于变分形式 (5) 的间断有限元离散，形成刚度矩阵A及右端项b；

步骤4. 利用线性解法器求解线性方程组Ax=b；

步骤5. 利用解向量构造有限元解uh并计算误差；

步骤6. 分析误差关于p及h的变化。

2 数值算例与结果分析

取ξ1= 1,ξ2=−1，计算区域Ω=[0,1]2。取Rayleigh 波作为边值问题(1) 和(2) 的解析解[22]

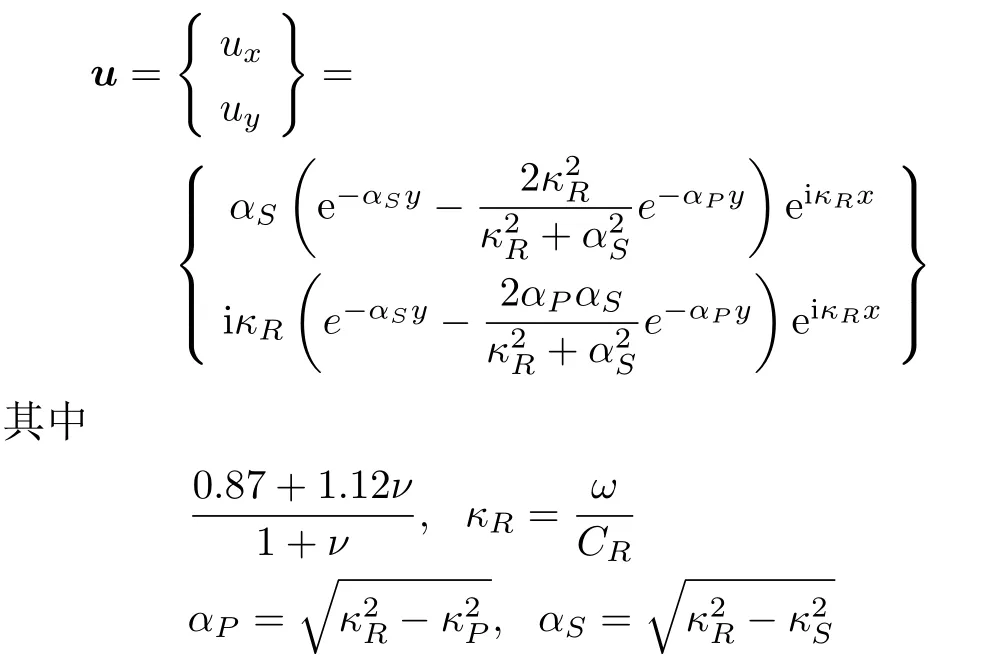
取E= 2.0×1011,ν= 0.3,ρ= 7800。将解析解u代入式(2)得到边界条件函数g，并将以上参数代入到式 (3) 得到边界正定矩阵σ。所有运算均在软件Matlab 上实现。

表 1、图 1 和图 2 分别给出了数值解关于单元基函数个数p的误差。数值结果表明数值解误差关于单元基函数个数p是指数收敛的。

表1 数值解关于单元基函数个数p 的误差

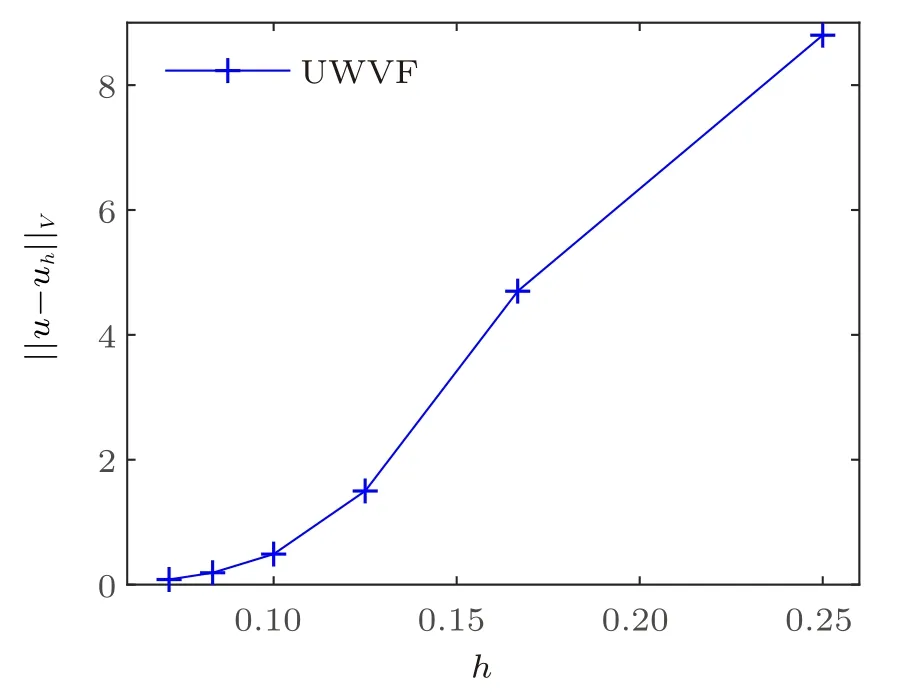
图1 数值解关于单元基函数个数p 的误差

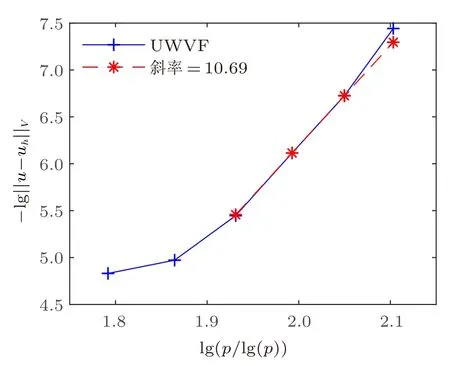
图2 对数下数值解关于单元基函数个数p 的误差

表2、图 3 和图 4 分别给出了数值解关于网格步长h的误差。数值结果表明数值解误差关于网格步长h是代数收敛的。

表 2 数值解关于网格步长h 的误差

3 结语

基于间断有限元方法构造数值求解弹性波方程的平面波超弱变分方法，实现了模型参数输入、网格剖分、平面波离散系统的生成及求解、误差计算和输出功能，具有良好的算法迁移、推广能力。该算法在“偏微分方程数值解”的课程教学中达到了以下目的：

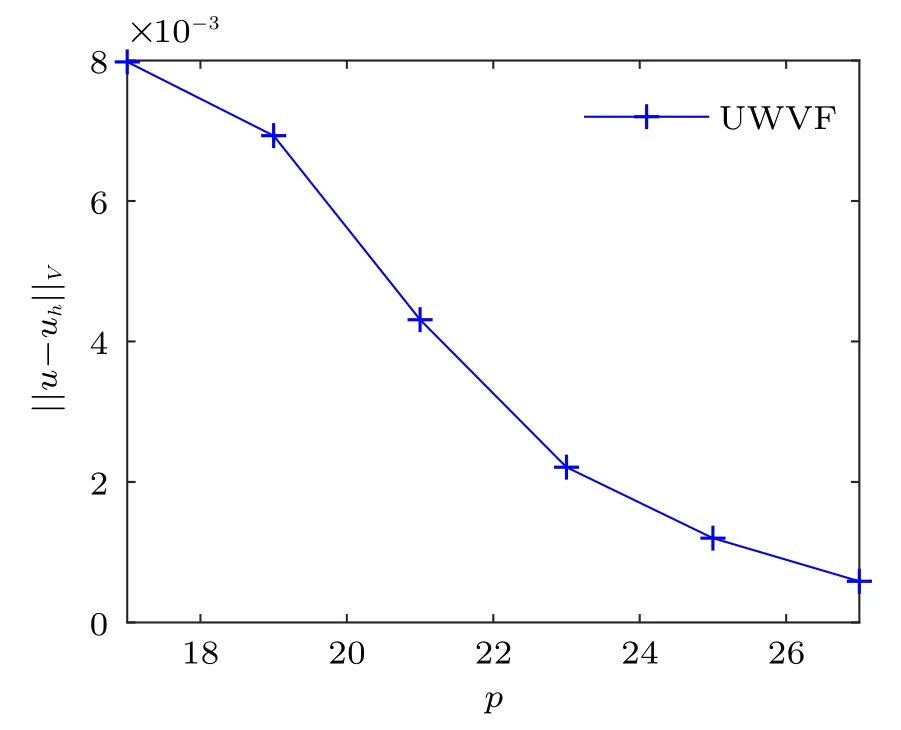
图3 数值解关于网格步长h 的误差

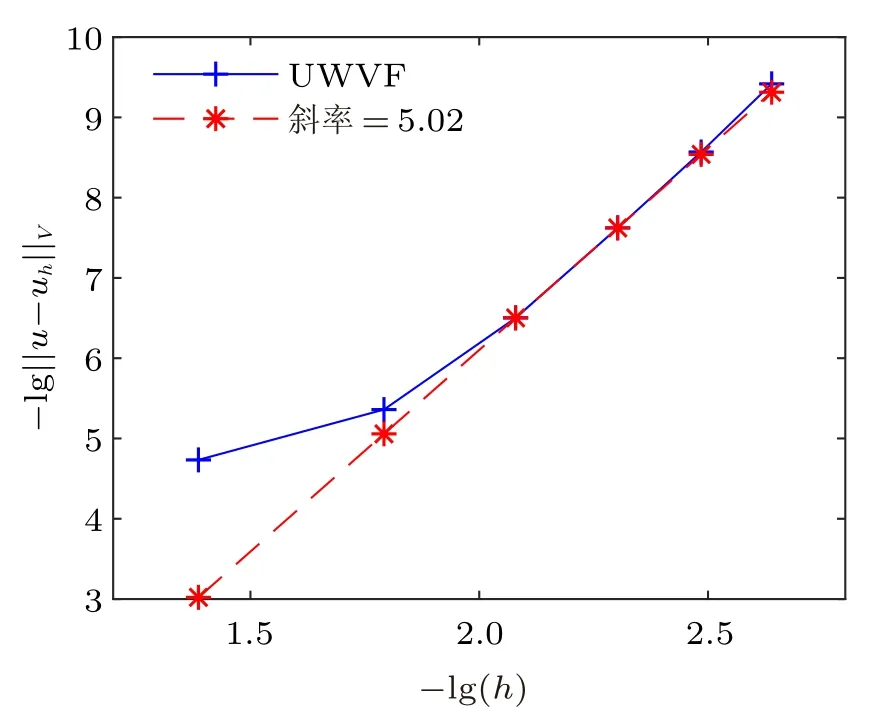
图4 对数下数值解关于网格步长h 的误差

(1)掌握间断有限元方法的思想，能够区分其与其他离散化方法的不同，使学生对算法加深理解。

(2)借助于代码实现，掌握间断有限元离散化方法的实现细节，特别是单刚合成总刚、线性方程组的求解等。

(3)借助于数值解误差的图形分析，使学生掌握数值解误差的收敛阶验证方法。

将该数值离散化方法应用于课程教学和实验教学中，对学生深入理解基础理论知识和掌握相应的实验方法有积极的作用，可以激发学生的科研兴趣和创新意识，提高学生的创新能力。目前，在此教学实验的基础上，我校学生正着力于实现复杂的三维区域网格剖分，取得了较好的实验成果。