认知无线网络中基于能量采集的单向中继选择与功率分配方案
李丽,曾凡仔,徐纪胜
(1.湖南大学信息科学与工程学院,湖南长沙 410082;2.湖南邮电职业技术学院,湖南长沙 410015)
当认知无线网络中主用户(Primary User,PU)收发机之间的信道增益很弱且无法配置多天线时,可以利用协作通信改善网络性能,提高频谱利用率.当前认知无线网络有三种频谱共享模式:交织模式、衬底模式和覆盖模式[1].中继选择以及中继节点的能量供给是协作通信提升网络性能的关键.文献[2]研究了衬底模式下协作中继选择策略.文献[3]研究了覆盖模式下的一种资源调度方案.文献[4]研究了混合衬底、交织模式下的动态频谱感知与访问模型.中继节点的能量供给对于认知无线网络十分重要,一旦中继节点的能量消耗殆尽,则数据传输将会被迫中断,而能量采集技术为中继节点的长期运行提供可能[5].文献[6]给能量采集和信息传输的同时执行提供了理论可能.文献[7]构建了一种新的能量采集网络系统,在干扰低于设定阈值的情况下次用户(Secondary User,SU)与PU 可在相同的频谱上同时传输数据.
由于实际电路的限制,难以实现同时能量采集和信息传输,文献[8]提出了一种采用时间切换中继和功率分裂方案.将传输时间划分为两部分分别用于能量采集和数据传输;将无线射频信号分为两部分数据流分别用于能量采集和信息解码.文献[9-[10]对时间切换中继方案进行了研究,但没有考虑能量效应.文献[11]分析了具有无限电池容量的时间切换和功率分裂中继方案的能量效率.文献 [12]在nakagami-m 衰落信道下分析了认知无线网络的中断概率.文献[13]主要研究了通过优化时间分配最大化PU 吞吐量.
本文研究不完美信道状态下,PU 和SU 都进行能量采集且SU 利用功率分裂技术采集能量和解码信息场景中的联合中继选择与功率分配方案,该方案通过最优化方法从多个SU 中选择最佳信道和能量状态的SU 作为中继协作传输,在实现系统能量效率最大化的同时保障PU 吞吐量最优.
1 系统模型
1.1 传输模型
PU 系统模型如图1 所示,包含一对PU 收发机和N 对SU.考虑基于能量采集的认知无线网络的单向中继协作传输方案,即从源节点经过中继节点到目的节点的信号单向传递.单向中继协作有半双工和全双工两种模式,本文采用半双工模式.此外PU拥有授权频谱且总是有数据传输,SU 作为中继候选并协助PU 传输数据来换取接入频谱的机会.
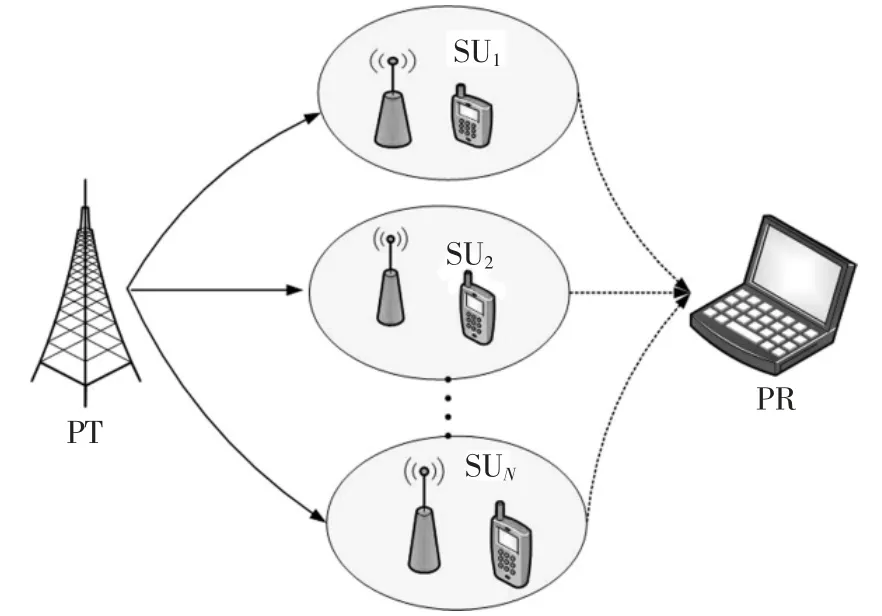
图1 主用户系统模型Fig.1 PU System model
如果接收信号能量消耗忽略不计,则PU 接收机和SU 接收机不需要能量采集设备,但PU 发射机和SU 发射机需配置能量采集设备,且采集能量多少决定是否参与数据传输和处理过程.假设PU 和SU 的电池存储容量有限,存储容量最大值分别为BPT,max和BSUn,max.
PU 和SU 都是以时隙模式运行,时隙传输模型如图2 所示.传输时隙间隔相等,每个时隙包括三个阶段且总的传输时长为J 个时隙.

图2 时隙传输模型Fig.2 Time slot transport model
第一阶段,PU 发射机和SU 发射机进行能量采集并存储在各自的电池中.
第二阶段,PU 发射机传输数据到SU 发射机,SU 采用功率分裂技术将接收到的信号划分为两部分数据流:一部分用来采集能量,另一部分解码PU信号.SU 发射机用于能量采集和解码信号的功率分裂比分别为ρE和ρI.假设所有的SU 发射机都可以成功解码PU 的发射信号.为了消除SU 之间的传输干扰,每次只有一个SU 发射机被选中协助PU传输数据.
第三阶段,被选中的SU 利用第一阶段采集的能量转发接PU 数据.PU 发射机保持静止,PU 接收机接收SU 发射机转发的数据.
1.2 信道模型
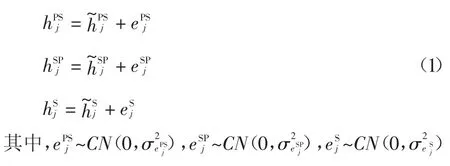
SU 采集无线电射频信号能量且将接收到的信号分裂为两个数据流,假设有N 个离散功率分裂比

2 系统能量与数据速率分析
2.1 系统有效能量
在第j 个时隙内,节点N∈{PT,SU1,SU2,…,SUN} 的电池能量为BN,j.假设存储能量是线性变化的,且不能超过最大存储能量BN,max,则有:
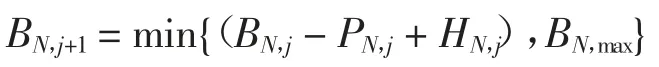
假定采集的能量HN,j≤BN,max且HN,j为一种均值为HN=E{HN,j}的遍历随机过程,其中E{·}表示期望值.令BN,1=HN,0≥0 表示节点开始传输之前的可用能量.
当PU 发射机发射无线电射频信号时,SU 发射机接收信号并采集能量,则采集的瞬时能量值为:
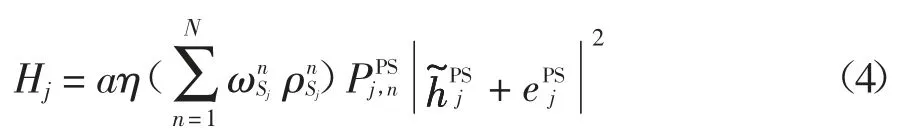
式中:η∈(0,1)为能量转换效率,a 表示第一阶段的时间比值=1 则为选择STj且以进行功率分裂,否则=0.采集的瞬时能量值是一个随机变量,因此能量中断可能发生.根据文献[11]可知采集的能量值表达式近似为:


2.2 系统有效数据速率
若将系统噪声归一化,则PU 发射机和SU 发射机之间的瞬时数据速率可以表示为:


3 中继选择和功率分配方案
3.1 系统能量效率最大化
系统的能量效率定义为PU 和SU 消耗的每焦耳能量可以成功转发的比特的平均数.中继选择和功率分配策略必须满足PU 和中继SU 的服务质量要求,且消耗能量必须低于采集的能量.据此需要优化三个变量,分别是中继选择策略ω、功率选择策略P 和时间参数选择策略a.给定∈{0,1},令P=表示从PU 发射机到中继和从中继到PU 接收机的传输功率集合是功率分裂比.本文假设SU 作为中继的发射功率为恒定的,则系统能量效率最大化问题可以表示为:

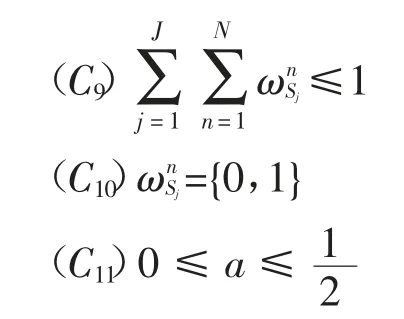
式中:约束C1和C4分别指的是PU 和SU 的最小数据传输速率约束,即服务质量要求.C2和C3是指用于消除C1中的最小函数值代数式.C5表示能量约束.C6~C8表示PU 和SU 中继传输功率约束.C9和C10约束表示PU 最多只有一个中继.C11表示时间分配长度约束.

则优化问题(14)的对偶问题为:

求解优化问题(14)时,首先确定一个常数值,其次根据拉格朗日对偶算法求解,然后可以通过对a 迭代求解问题(16).在每次迭代中,利用Karush-Kuhn-Tucker 条件计算最优分配功率参数和时间系数,且最优解表示如下:


而a 最优解a*可用牛顿迭代法求解(19)式得到.
假设选择STj作为中继且功率分裂比为,当满足中继选择准则时,有:

对偶问题(16)的最小化则采用共轭梯度方法,其拉格朗日算子的更新如下:
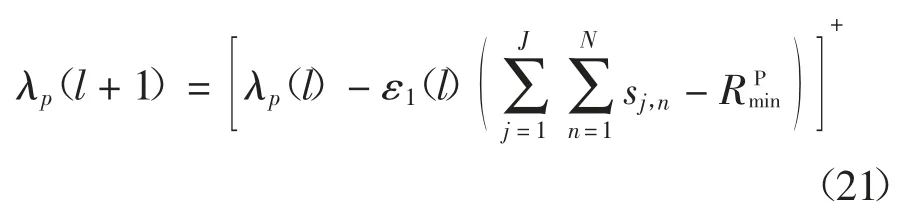
利用类似方法可以推导出其它参变量.
3.2 PU 系统吞吐量最大化
假设已知信道状态信息(CSI)、PU 发射机和SU的能量采集时间、SU 的功率分裂比,为使截止到第J个时隙的数据传输总比特数最大,则构造PU 吞吐量最大化问题如下:



此时,优化问题(30)是一个凸混合整数非线性规划,采用广义Benders 分解法(GBD)将优化问题(30)分解成一个基本问题和一个主要问题求解.二元变量ωn,j可以通过求解主要问题而获得,而PPT,j和PSUn,j则可以通过求解基本问题而获得.GBD 算法反复迭代求解基本问题和主要问题直到它们的解收敛.
1)基本问题(第i 次迭代)
基本问题是一个关于变量PPT,j,PSUn,j,λPT,j,λSUn,j的凸优化问题,可以通过凸规划求出最优解.令表示在第i 次迭代中的最优解.
2)主要问题(第i 次迭代)
利用基本问题的拉格朗日算子变换构造主要问题.基本问题的拉格朗日算子为:

式(45)为一个ψM和ωn,j的混合整数线性问题,可以通过现有的标准优化工具箱求解.

表1 GBD 算法Fig.1 GBD algorithm
4 数值仿真分析
4.1 数值仿真参数
通过数值仿真分析所提出的次用户中继选择和功率分配算法的性能.假设平均采集能量效率是HPT=HSU1=…=HSUN=0.55 且HPT,j和HSUN,j相互独立,取值为{0,0.65,1},其中每个取值概率相等.假设BPT,max=BSU1,max=…=HSUN,max=120.能量参数分布的均值分别为0.01、0.25、0.5、0.75、0.99,PU、SU 容许的中断概率为0.01.能量采集过程的中断概率为0.1.能量采集随机变量的方差σ2为0.01.
考虑指数分布信道条件,分析不同的次用户数目N 和信道条件下所提出的方案的性能.场景一中假设N=1 且=0.8.场景二中假设N=3,其中第一条链路的信道状态条件和场景一相同,假设=0.9.场景三中假设N=5,且前三条链路和场景二的信道状态条件相同=0.95.通过数值仿真模拟随机产生信道状态条件和采集能量的多次实验获得了平均吞吐量.
4.2 仿真结果
图3 为总的传输比特数目与时隙数目的关系曲线.从图3 可知,本文提出的联合功率分配和中继选择方案,吞吐量随着时隙和次用户中继个数的增加而增加.
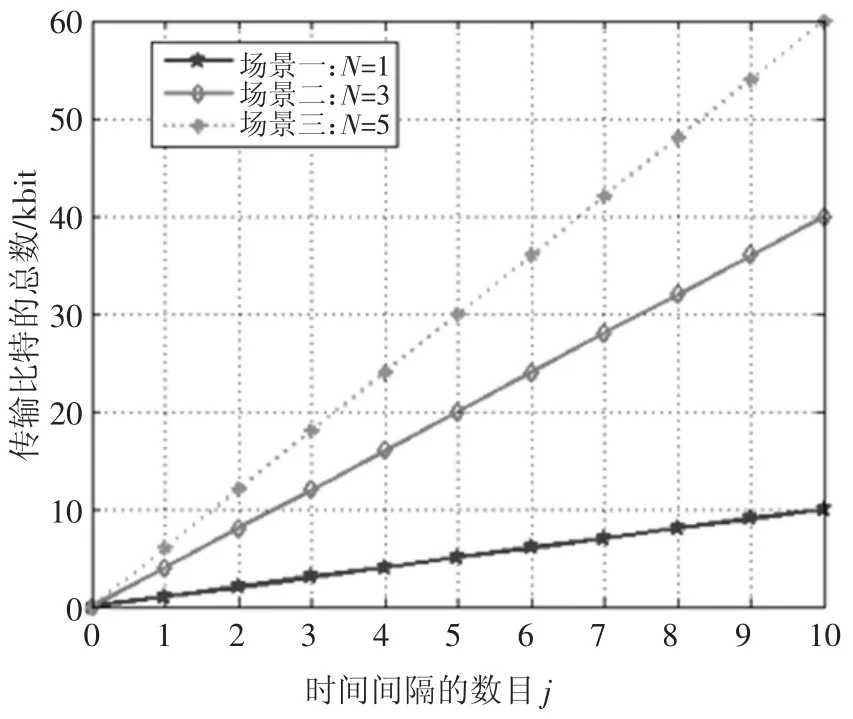
图3 传输比特的总数目与时间间隔的数目关系Fig.3 The number of transmitted bits vs the number of time intervals
图4 为在两种不同传输模式下系统有效吞吐量与时间分配系数的关系曲线.非协助传输模式中PU在没有SU 的协助情况下独自传输数据.PU 完成数据传输后,SU 感知到频谱空闲状态再接入频谱进行数据传输.协作传输模式即本文提出的单向中继协作传输.从图4 可知系统有效吞吐量首先随着时间分配的增加而增加,但由于传输功率和传输速率限制,当时间分配系数增加到一定值后,系统的有效吞吐量开始下降.这是因为采集能量值与采集能量的时间相关,所以用于传输时隙中的能量不足导致系统用户服务质量得不到保障.而单向中继协作传输能够合理有效地分配时间和频谱,提高频谱利用率,所以在单向中继协作传输模式系统的有效吞吐量明显高于主用户独自传输的非协作模式.

图4 系统的有效吞吐量与时间分配系数的关系Fig.4 Effective throughput of the system vs time allocation coefficient
图5 为PU 有效吞吐量与SU 数目的关系曲线.因为信道条件和能量约束条件是有限的,所以PU 的有效吞吐量无法满足.因为PU 和SU 的协作在能量信道条件有限情况下能够更有利于数据传输,所以从图5 可知,在SU 的帮助下PU 的有效吞吐量随着SU 的数目增加而增加,且最优中继选择策略明显优于随机中继协作方案.
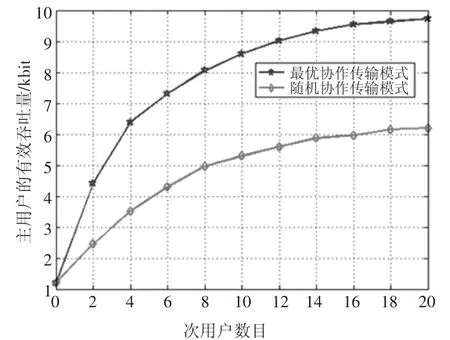
图5 PU 的有效吞吐量与SU 数目的关系Fig.5 Effective throughput of PU vs SU number
图6 为系统平均能量效率与SU 的数目的关系曲线.由图6 可知最优中继选择策略下系统平均能量效率明显优于中继协作方案.这是因为随机中继协作传输仅基于随机信道条件和SU 选择方案最大化用户或者系统的能量效率,可能会随机选择一个信道状态差的SU 作为中继协助传输,导致能量资源浪费.本文所提的中继选择策略虽然只考虑了能量采集系统特性,但是可以自适应地利用有效的信道状态和能量采集信息优化能量效率,选择信道状态较好的SU 并分配合适有效的能量从而获得最优传输性能.

图6 系统平均能量效率与SU 数目的关系Fig.6 Average energy efficiency of the system vs SU number
5 结论
本文提出一种基于能量采集的单向中继选择和功率分配方案,构造了所提方案的系统能量效应优化问题.应用分式规划变形和拉格朗日对偶方法以及广义Bender 分解方法求解优化问题得到最优解.数值仿真分析验证了所提方案的性能及求解方法的优势.

