不完美排错下测试覆盖相关的软件可靠性模型
张策,吕为工,邱忠银,高天翼,江文倩,孟凡超
(哈尔滨工业大学(威海)计算机科学与技术学院,山东威海 264209)
软件测试是软件可靠性不断增长的过程,是提高可靠性必不可少的关键环节.软件测试过程是软件测试人员在某种测试环境下,按照预定的测试策略或计划,执行测试案例,发现与检测软件运行过程中的失效,定位、收集和记录故障,并进行故障修复的过程.整个过程大致由三个部分组成,即故障检测过程FDP(Fault Detection Process)、故障分析过程FAP(Fault Analysis Process)和故障修复过程FCP(Fault Correction Process)[1].图1 描述了软件测试与排错过程,可以看出,随着故障被不断的检测和修复,软件的可靠性得到持续提高.

图1 真实软件测试过程中存在不完全排错与引入新故障情况Fig.1 Incomplete troubleshooting and introduction of new faults during real software testing
由于软件测试与排错的复杂性、随机性和不确定性[2-5],检测到的故障在修复阶段可能没有成功排除,出现排错的不完全现象,如图1 中上面的反馈线;另外,在故障的修复过程中,由于程序的内在结构逻辑可能被破坏,从而存在引入新故障的可能[6-7],如图1 中下面的反馈线.包括这两种情况等实际测试情况在内的复合现象通常被称为不完美排错现象.因此,不完美排错[5,8-12]是更加靠近真实软件测试过程的研究,能够描述更多的实际情形,得到了科研人员的重视.软件可靠性增长模型SRGM(Software Reliability and Growth Model)[13-15]可用来对软件测试过程进行建模,通过数学手段来定量描述故障检测、修复等关系,是对软件可靠性进行有效度量与预测的重要工具.在现有SRGM 研究看来,不完美排错是对实际软件测试过程的一种近似抽象,包括排错的不彻底现象[16]、引入新故障现象[9-10]或者是软件中总故障数量a(t)的不断增长现象[17].这些研究从不同角度和内容对测试过程进行了不完美排错建模,有力地推动了SRGM 的发展,但对不完美排错的全面准确描述还不够深入.例如,很多大型软件的测试过程中,故障排错的不完全与引入新故障通常是同时存在的,二者相互交织在一起.从测试覆盖角度来看,包括经典的G-O(Goel L -Okumoto K)模型[18-19]在内的很多完美排错和不完美排错模型,均默认或假定测试覆盖满足100%,但显然这是不切合实际的.测试覆盖针对程序结构进行测试策略下的测试,涵盖语句覆盖、分支覆盖、条件覆盖、路径覆盖、数据流覆盖、函数覆盖、调用覆盖,因此从测试覆盖的角度研究可靠性可以更加细腻地剖析可靠性的变动.事实上,软件测试过程是较为复杂的随机过程.为了得到更加有效的可靠性模型,就需要对测试过程中的随机因素加以考虑.
本文在现有研究的基础上提出一种全面考虑不完美排错的软件可靠性过程分析方法,明确考虑到了测试覆盖,所提出的模型能够更加准确地描述软件测试过程.
文章结构安排如下:第1 节对考虑真实测试过程的不完美排错进行建模,提出了一种不完美排错下测试覆盖相关的软件可靠性增长框架模型,进而给出了具体的测试覆盖函数相关的可靠性模型;第2节通过公开发表的失效数据集验证了所提出模型的有效性与合理性.最后总结了全文,并指出后续研究方向.
1 不完美排错下测试覆盖相关的软件可靠性增长框架模型
1.1 基本假设
基于对测试环境的认知,遵循SRGM 研究所作假设的常规共识,考虑测试覆盖下的不完美排错模型假设如下[18,20-24]:
1)软件失效随机发生,故障检测与修复过程服从非齐次泊松过程NHPP(Non-Homogeneous Poisson Process)[12,18,25],即到t 时刻累积检测出的故障数N(t)服从期望函数为m(t)的NHPP 分布,满足m(t=0)=0,则利用NHPP 基本性质,能够得到t 时刻检测到k个故障的概率以及m(t)与故障检测率λ(t)的基本关系:

2)软件失效由软件中剩余的故障引发;
3)在时间区间(t,t+Δt)内,最多发生一个故障,且所检测到的故障数量与当前剩余的故障总数成比例;
4)在时间区间(t,t+Δt)内,被修复的故障数量与被检测的故障数量成比例;
5)故障修复的过程中,存在引入新故障的现象,引入的故障数量与累积修复的故障数量成比例.
1.2 不完美测试框架模型
令m(t)和r(t)分别表示截止至t 时刻累积检测到和修复的故障数量,a(t)表示t 时刻软件中总的故障数量.则基于上述假设,建立了下面的基于故障检测率函数b(t)、故障修复函数p(t)和新故障引入函数γ(t)的故障检测、修复与引入模型,如式(3)所示.
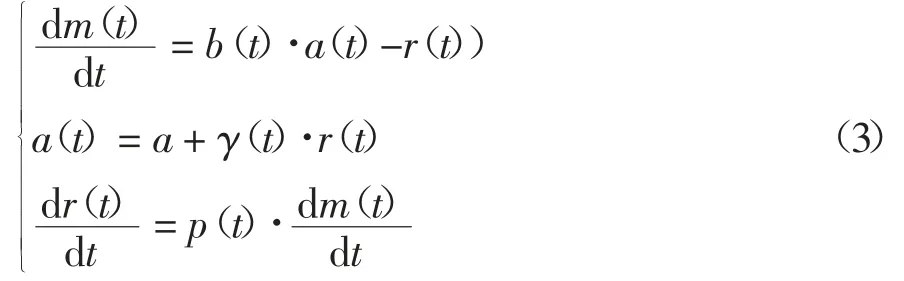
式(3)中第一个方程基于第三条假设,描述了t时刻检测的故障数量与剩余故障数量的关系;第二个方程基于第五条假设,从t 时刻新增加的故障角度建立了总故障个数a(t)的表达式;第三个方程基于第四条假设,对Δt 时间内检测的故障数量与修复的故障数量进行建模.
b(t)是故障检测率,表示测试人员在测试环境下运用测试技术检测出故障的概率,其可以从多种角度来进行设定.当考虑测试覆盖时,故障检测率b(t)可表示如下:

c(t)表示截止至t 时刻已经被(测试案例)测试的代码所占的百分比;1-c(t)表示到t 时刻尚未被测试的代码所覆盖的比例.显然,c(t)的导数c′(t),则表示t 时刻点上的测试覆盖率.易知,故障检测率FDR(Fault Detection Rate)[26]与c′(t)成正比例,且与1-c(t)成反比例,b(t)=c′(t)/[1 -c(t)].r(t)表示新故障引入率,p(t)表示t 时刻故障被成功修复的比例函数.
此微分方程组的边界条件为:

这里,采用如下过程进行求解,为方便令:


将式(9)代入式(7),则有:
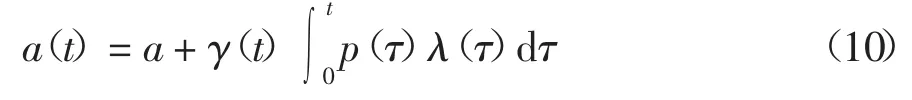
式(10)~(9)代入式(6)可得:

将式(13)代入式(11)得:
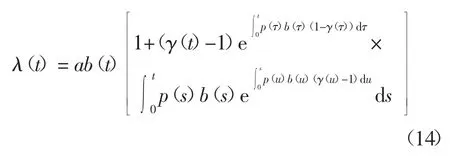
由此求解得到统一的测试覆盖函数下,考虑故障不完全修复与新故障引入的不完美测试模型如下:
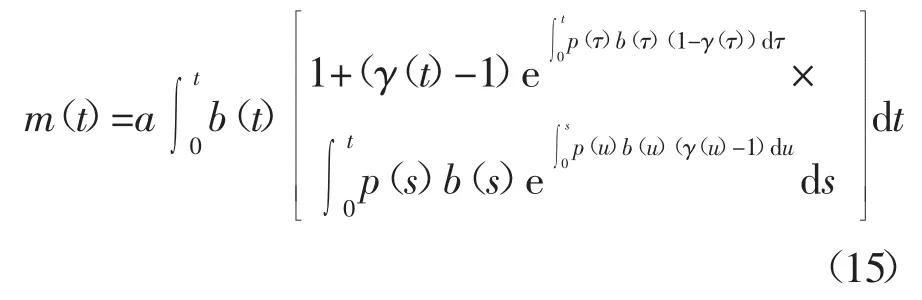
考虑到累积检测出的故障数量与失效率之间存在着微分关系如式(2)所示,则可得失效率λ(t)为:

相应地,可求得软件中总故障数量a(t)和累积修复的故障数量r(t):
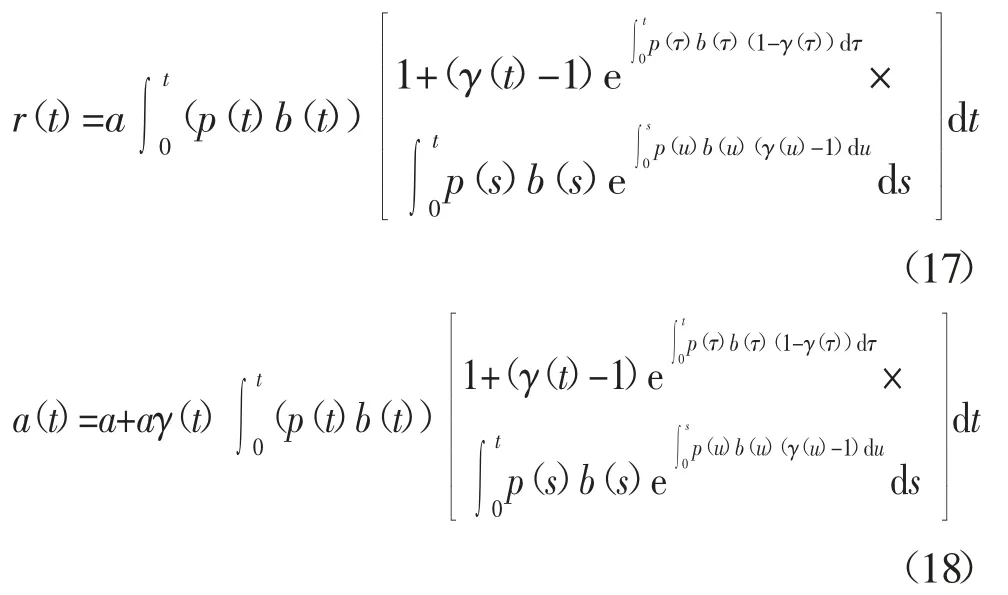
至此,完成了测试覆盖函数下考虑故障不完全修复与新故障引入的不完美测试框架模型的构建,得到了SRGM 研究中重要的关键内容:m(t)、r(t)和a(t).从测试过程的整体来看,截止t 时刻,累积修复的故障数量r(t)小于等于累积检测的故障数量m(t),m(t)小于软件中故障总数.将上述模型简记为TCMID(Testing Coverage Software Reliability Model under Imperfect Debugging).
测试阶段的软件可靠性表示为R(x|T),即假定软件上一次失效时间是T(T≥0,x>0),依据NHPP基本性质,可得在(T,T+x)内的软件可靠性表示为:

若假定从T=0 开始,则m(t)=0,将式(15)代入式(19),则可以得到更易理解的可靠性R(x),如式(20)所示:
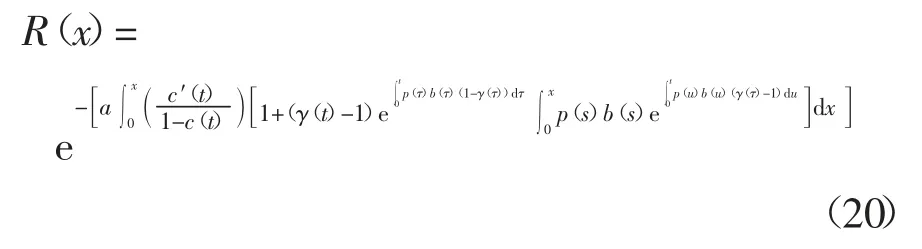
1.3 关于模型的柔韧型讨论
TCM-ID 采用微分方程组的形式对不完美排错下的测试过程进行建模,其中融入了故障排错率p(t)、故障检测率b(t)和新故障引入率λ(t),因此求解得到的m(t)、r(t)和a(t)是多参数的融合体.为此,可以看出该模型是具有较强柔韧性的框架模型,可以支持一系列的不完美排错相关的具体模型的构建.
1)采用方程组的形式建立了不完美排错相关的软件可靠性模型;
2)关键的故障数量表达式(m(t)、c(t)和a(t))均是通过求解得出,且具体由3 个参变量函数来决定,即故障检测率b(t)、故障排错概率p(t)以及故障引入率λ(t),这些参变量函数可根据实际情况进行设定,这为模型的框架性、统一性和柔韧性提供了支撑,为SRGM 所关注的m(t)等信息提供了更为客观的依据,从而使其更加直接地受制于实际因素;
3)故障修复过程中存在故障的引入,因此,单位时间内新增加的故障数量应与累积修复的故障数量成比例.
1.4 测试覆盖函数视角下TCM-ID
故障检测率FDR:b(t)是可靠性建模中必不可少的构成元素,其描述了测试环境下故障被检测出来的能力.当前研究中以人为设定FDR 为某种函数为主,且为求解简便,多以b(t)=b 为常见.显然,由于测试环境的复杂性,测试阶段、测试策略等因素的不同会使FDR 呈现多种变化形式.文献[27-28]认为测试覆盖函数与FDR 紧密相关,可以成为FDR 建模的元素,并提出c′(t)/(1-c(t))可用来度量t 时刻的故障检测率b(t).c′(t)描述了测试用例[29]的执行情况,通过c(t)的变动可以获得不同的FDR 函数.这样,可以得到下述的不完美排错过程模型:

依据上述求解过程进行求解,可以得到测试覆盖函数下的不完美测试模型中的m(t):

至此,从测试覆盖函数c(t)的角度得到了SRGM研究中的关键待求变量m(t).通过设定各类测试覆盖函数c(t),可以得到一系列相关的m(t).为简化计算,不妨令p(t)=p,γ(t)=γ.这里令a(t)=(1 -ebtc)[30],则可求得m(t)如下:

可以看出,本文所提出的模型在测试覆盖函数视角下,将可靠性研究由传统的FDR 相关演进为不完美排错下测试覆盖相关的可靠性模型.
2 数值算例
2.1 参与比较的模型
这里选定了一系列典型的不完美排错模型参与比较,以对比模型之间的性能差异,如表1 所示.

表1 参与比较的模型Tab.1 Participating models for comparison
选取4 个已被广泛用来进行验证可靠性模型性能的失效数据集DS1[24],DS2[35],DS3[36],DS4[22],它们均来自国际知名公司在系统开发过程中所搜集的软件测试失效数据,具有广泛的代表性,可以表征多样的软件测试场景;同时,选取通过可靠性过程仿真获得的失效数据集DS5[37]进行同步验证,该数据集来自基于率函数对不完美排错下的软件测试情况进行仿真,更加靠近真实情况.
2.2 比较标准
采用均方误差值(Mean Square Error,MSE),Variation,RMS-PE 和回归曲线方程的相关指数(Rsquare)度量曲线拟合效果,利用相对误差(Relative Error,RE)度量模型的预测能力.


式中:yi表示到ti时累积的失效个数,m(ti)表示到ti时利用模型得到的估算值,k 表示失效数据样本数量.显然,MSE,Variance,RMS-PE 和BMMRE 的值越小,R-square 值越接近于1,拟合效果越好;RE 越趋近于0,模型预测效果越好.
2.3 性能验证
为了验证所提出模型的有效性,将表1 中的模型在5 个公开发表的真实数据集DS1~DS5上进行实验.基于拟合得到的参数值,计算5 个失效数据中不同时刻各个模型的m(t),绘制出m(t)与真实失效数据间的拟合曲线,如图2 所示.
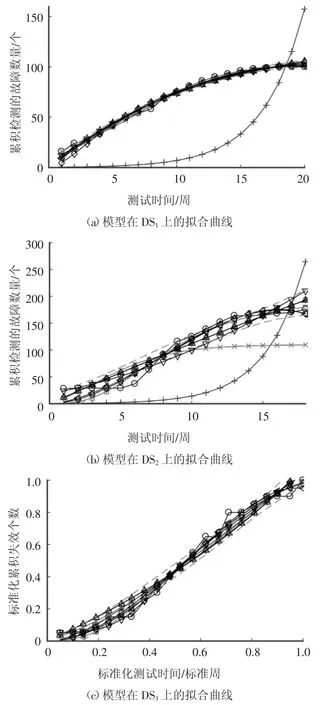
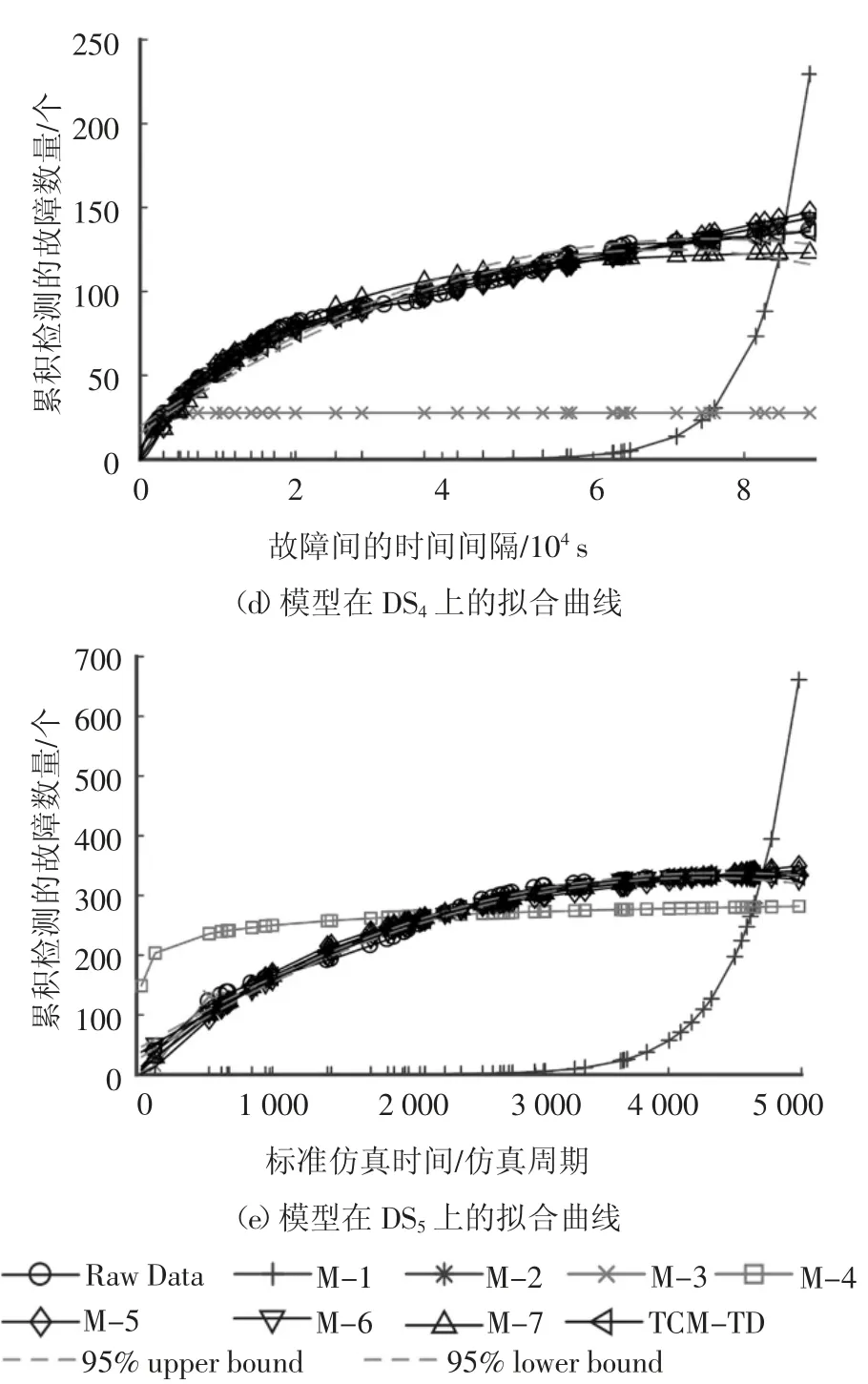
图2 各个模型的累积检测故障数量m(t)的拟合曲线Fig.2 Fitting curve of cumulative detection failure number m(t)of each model
从图2 可以直观看出:
1)在DS1、DS2、DS4和DS5上,个别模型已经严重偏离真实的失效曲线(M-1 模型与DS1、DS2、DS4和DS5上的失效数据曲线走势严重不符;M-3 模型在DS2和DS4上也产生了同样的情况),表明模型已经严重失真.在DS3上参与比较的模型,在整体趋势上与真实的失效数据相一致;
2)在DS5上,本文所提出的模型同样表现出优秀性能,与失效数据曲线走势保持一致,重叠度高;
3)在所有5 个数据集上,本文提出的模型TCMID 与真实的失效数据曲线有较高程度的重合,这表明该模型具有较好的拟合性能.
为了进一步区分不同模型的性能差异,这里定量化地计算并列出了各模型在5 个拟合标准上的数值,如表2 所示.
从表2 可以直观看到,与图2 曲线相一致,个别模型的拟合指标数值不理想,反映出其性能较差
(M-1 模型在DS1、DS2和DS4上性能欠佳;M-3 模型在DS2和DS4上也有同样的情况).在DS2数据集上,本文所提出的模型在4 个指标上均优于其他模型(MSE,Variance,RMS-PE,BMMRE 数值越小表明模型性能越好:R-square 越接近于1 表明模型性能越好),并在数值上具有明显的比较优势,显示出了该模型优异的性能.在DS3上,所提出的模型TCM-ID在前4 个指标上同样表现出了优秀的性能;在BMMRE 指标上与其他模型处于相同量级,没有出现明显的差异,综合来看,可以表明模型TCM-ID 具有优秀的性能.在DS4上,M-5 和本文所提出的模型均表现出了优异的性能,二者在数值上较为接近,处于同一数量级别(M-5 在MSE,Variance,RMS-PE 这3个指标上略优于TCM-ID,TCM-ID 在R-square 和BMMRE 上优于M-5),显示出了TCM-ID 的良好性能;综合全部数据集来看,M-5 仅仅在DS4上表现优秀,表明该模型具有很强的不稳定性能,难以适应更多的数据集.因此TCM-ID 的性能要明显优于M-5.同样,M-4 也仅仅在DS1上显示出了优秀的性能,同样具有较强的随机性,不如本文所提出的模型具有在多个数据集上连续优秀的稳定性.在仿真失效数据集DS5上,TCM-ID 在5 个具体的指标上均优于其他7 个模型,同样显示出了优秀的性能.DS5来自于对不完美排错软件测试过程的仿真,这与本文建立的不完美测试框架模型具有一致性,对更加靠近真实故障检测、修复与引入的实际情况进行了准确描述.
综上可以看出,本文所提出的模型TCM-ID 能够保持连贯的稳定性能,在全部失效数据集上或者处于最优或者处于良好(且与某个数据集上表现优秀的模型之间差异较小).这种原因可以解释为:
1)TCM-ID 在建模中充分考虑到了排错的不完全性与排错过程中存在新故障引入这种真实存在的客观现象,将更多的软件测试过程中的随机性纳入到模型中,将不完美排错用微分方程进行了准确的建模.相比之下,M-4 与M-5 模型因缺少对真实不完美排错因素的考虑,或者仅从不完全排错或新故障引入某个单一方面建模,导致它们仅能在个别数据集上表现优秀.
2)在测试覆盖方面,本文的模型在建模过程中引入了测试覆盖函数,用以描述和建模测试过程中故障被测试覆盖从而被检测出来的程度,更加精准地刻画了真实测试的情形;相比之下,其他模型认为测试覆盖是100%,这与真实的测试过程并不相符.
所有这些差异,使得其他模型的综合性能劣于本文所提出的模型.
关于模型的预测性能,图3 分别绘制了不同模型在5 个失效数据集上的相对误差RE 曲线.整体上看,在失效数据集的后半程时间内,模型开始进行快速地收敛,逐渐向着0 曲线靠拢,表明其预测性能在提高.从图3 可以看出,本文所提出的模型能够较好地向着0 曲线收缩,特别是在测试时间过半之后收缩速度明显加快.
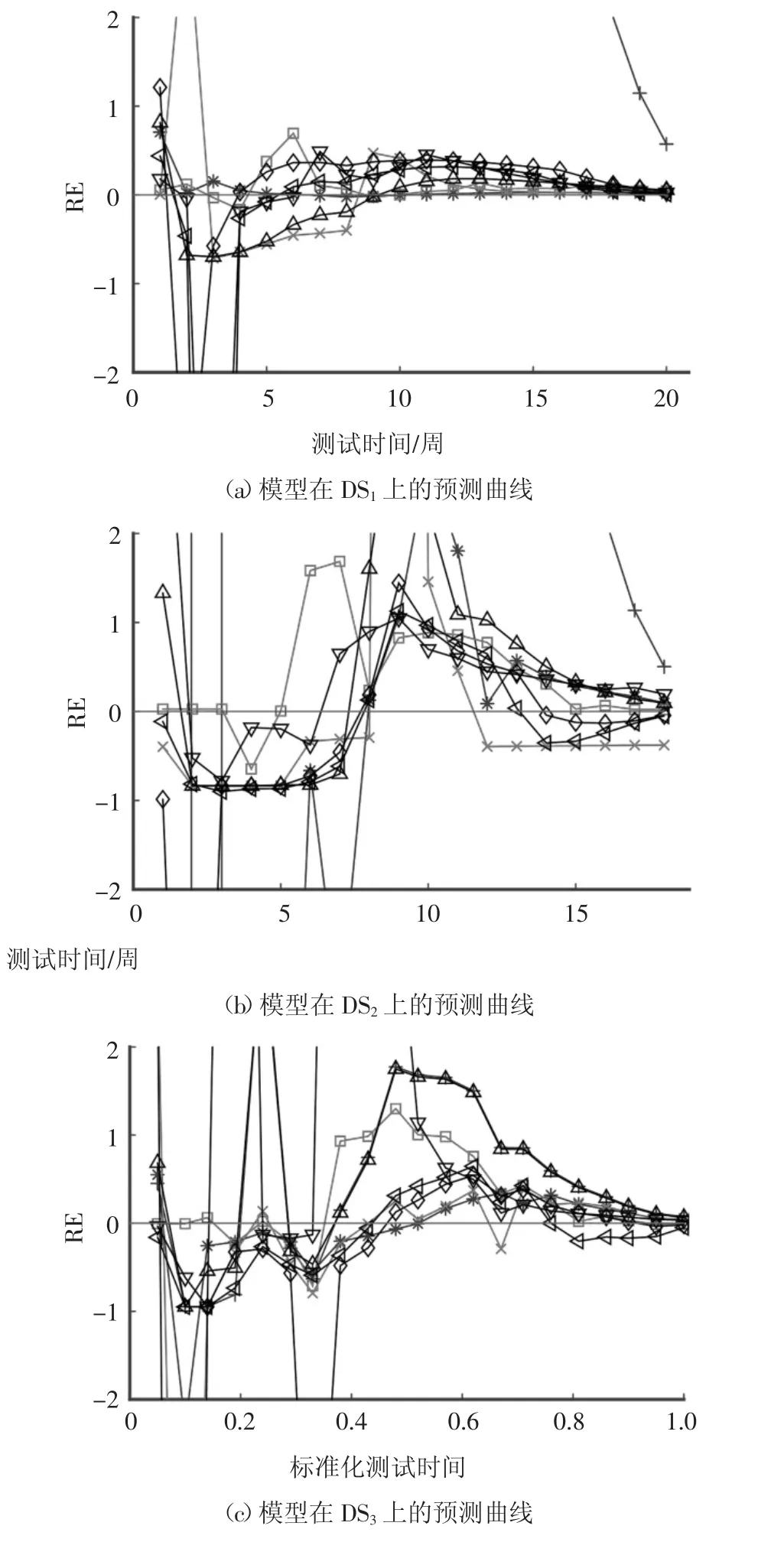
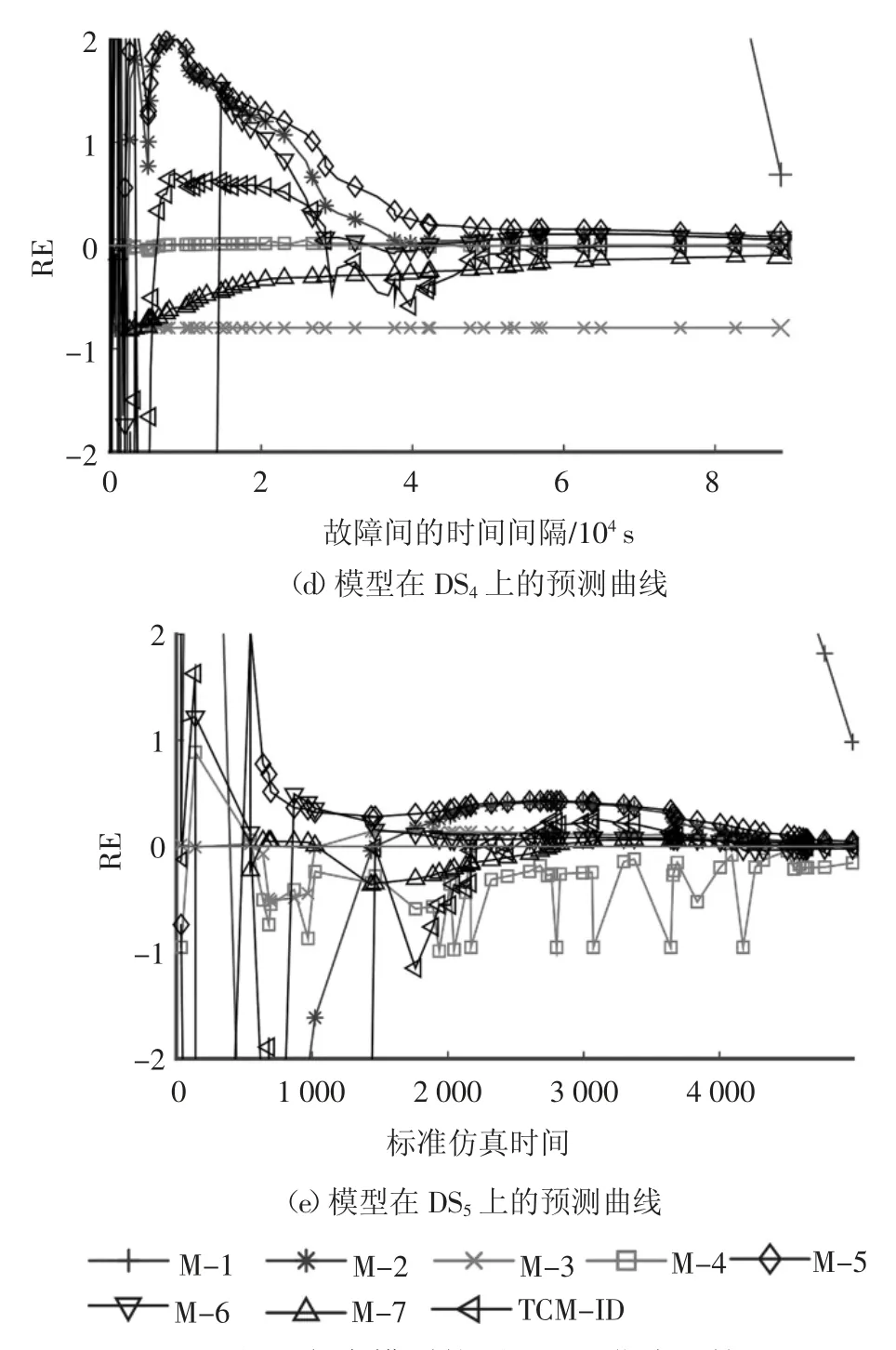
图3 各个模型的预测RE 曲线比较Fig.3 Comparison of prediction RE curves of each model
至此,从图2、图3 和表2 可以看出,本文所提出的模型充分考虑到了软件测试与排错过程的不完美特点,并将测试覆盖作为重要的影响因素进行考虑,所建立的模型具有较好的拟合与预测性能,整体上优于其他模型.
3 结论与下一步研究内容
针对测试环境的复杂性和随机性,以及当前研究所做假设偏离实际的问题,本文建立了涵盖故障检测、修复和新故障引入的统一的不完美排错框架模型,模型中融入了测试覆盖因素,使得测试中的实施细节得以在数学模型中呈现,进而从测试覆盖的角度研究分类模式下测试覆盖的能力,对可靠性性能影响评测进行了深入研究.因考虑到更多真实测试的随机性,本文所建立的模型不仅具有良好的柔韧性,在拟合与预测两个方面也均具有较好的性能,整体上优于其他模型.后续研究中,还应该深入钻研软件排错过程中的随机性(包括多个测试阶段内的延迟、多种测试覆盖类型函数等),以及针对大型开源软件和复杂网络软件的测试阶段可靠性建模与评测,同时要采用人工神经网络、遗传算法和随机过程等数学工具建立更加精准的验证模型.

