非自治时滞脉冲Cohen-Grossberg神经网络的p-阶矩指数稳定性
李 蕾
(淮北师范大学 数学科学学院, 安徽 淮北 235000)
Cohen-Grossberg神经网络模型(CGNNs)自提出以来很快在理论研究和工程应用中引起了广泛关注.稳定性是其关键特性之一,已受到不同领域学者的广泛关注[1-5].例如,Cao[6]得出了时变时滞递归神经网络的全局渐近稳定性判据.Shen[7]和Zhu[8]讨论了模型的指数稳定性. Sun[9]和Cao[10]研究了非线性时滞系统以及混合脉冲随机微分系统的输入-状态稳定性.由于在神经处理过程中存在时间延迟,因此在建模时有必要引入时滞.Liao[11]和Zhang[12]的研究表明,神经网络会因为一些外部输入而改变状态,这也说明了时滞对于神经网络的稳定性状态的重要干扰作用.在实际中,突然变化是瞬时发生,不能用纯粹的连续或离散模型来描述,需要引入一种新型的神经网络——脉冲神经网络,作为对此类现象的适当描述.Xu[13]和Li[14]研究脉冲模型的全局指数稳定性以及脉冲非自治系统的均方指数稳定性,为以后的论断奠定了理论基础.

1 预备知识
基于马氏切换的脉冲时滞CGNNs

r(t)为在M={1,2,…,m}取值的右连续的马氏链.系统各模型之间的转换概率为

为了证明结论成立,作出以下假设


xdi(x,r)≥di(r)x2.


|fi(s1)-fi(s2)|≤Fi|s1-s2| .


则系统(1)是p-阶矩指数稳定的,其中p≥2为正常数.
首先介绍引理.
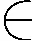
(1)
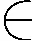

(2)
若初始条件满足

(3)



(4)
首先证明对于任意的正常数ε以及i=1,2,…,n,有
(5)
其中,K*=Kexp(ετ).
若式(5)不成立那么根据Ui(t)的右连续性,存在常数t*≥t0以及常数m,使
Um(t*)=yε(t*),D+Um(t*)≥D+yε(t*) ,
(6)
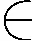
(7)
成立.
另一方面,根据Um(t)的定义可得
从而有

(x(t*),r(t*))+
继而可得

与(6)矛盾,所以式(5)成立,对于一切t≥t0令ε→0,从而可以得到
即
证毕.
2 主要结论
定理1若以下假设都成立:
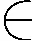
其中,



所以有






由Hölder不等式,可以得到

进一步可得

用数学归纳法证明对于所有的t≥t0,有
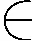

所以


由引理1可得

假设对一切m=1,2,…,k,有不等式
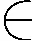
qik(x1((tk-τi1(tk))-),x2((tk-τi2(tk))-),…,xn((tk-τin(tk))-))]p≤

xj((tk-τ(tk))-)|p=

由数学归纳法,得

根据引理1可得



证毕.
注1:当r(t)为常数时,随机微分延迟系统退化为确定性系统,引理1中不等式退化为传统的Halanay不等式因此,传统Halanay不等式是引理1的特例,所以引理1所研究的范围更广泛.
注2:本文所研究的神经网络是非自治,当退化为自治系统时,其判断依据为
3 数值例子
令p=2,n=2,考虑以下模型
马氏链及各项参数分别为


f(x)=0.25x xR,h1(x1(t))=1+0.5sin(x1(t)),h2(x2(t))=1+0.5sin(x2(t))[0.5,1.5],τ(t)=sin≤1=τ,tk-tk-1=0.3k .
1) 若pik(x1,x2)=xi,qik(x1,x2)=2,对于任意的i=1,2,…,n,k=1,2,…,通过计算可以得到

令λ(t)=0.1,可以得到
显然,结果满足引理1的条件,因此由引理1可知该CGNNs是p-阶矩指数稳定.
2) 若
p1k(x1,x2)=0.25 exp(0.02k)x1-0.1 exp(0.02k)x2,
p2k(x1,x2)=-0.25 exp(0.02k)x1+0.18 exp(0.02k)x2,
q1k(x1,x2)=0.25 exp(0.02k)x1,q2k(x1,x2)=-0.25 exp(0.02k)x2,
对于任意的i=1,2,…,n,k=1,2,…,则由假设可计算出
令λ(t)=0.1,可以得到
所以对于任意的k=1,2,…,有
δk=exp(0.04k)≥max{1,exp(0.04k)(0.623+0.25 exp(0.2))},

由引理1得证模型的p-阶矩指数稳定性.
4 小 结


