基于EEMD 分解与PCA-FCM 聚类的岸桥减速箱故障诊断方法*

顾能华 ，侯银银 ，韩雪龙

(1.衢州学院 电气与信息工程学院，浙江 衢州 324000；2.国网浙江省电力有限公司衢州供电公司，浙江 衢州 324000)

0 引言

岸桥常作业于高速、重载、大冲击的工作环境中，其起升减速箱由于传动力矩大，且长时间受到强烈动载的振动冲击，是岸桥中最容易出现故障的部件之一[1]。因此，诊断监测岸桥减速箱的状态变得尤其重要。本质上,对减速箱进行故障诊断是一种模式识别问题，为了更准确地识别减速箱的状态，需要对减速箱振动信号进行有效的特征提取和更准确的分类。

起升减速箱振动信号为非平稳、非线性、非周期信号，传统的时域、频域以及时频域方法缺乏对非平稳和非线性信号的多分辨率分析和自适应处理能力[2]。HUANG N E 等[3]提出的经验模态分解(Empirical Mode Decomposition，EMD)由于其良好的自适应分解特性在处理非线性和非平稳信号时具有很大的优势。然而，EMD分解会产生模态混叠现象。WU Z 等[4]通过改进EMD 分解方法得到一种新的EEMD 分解法，能够有效解决该问题。王玉静等[5]通过EEMD 分解得到滚动轴承振动信号的固有模态函数，并结合峭度值、相关系数提取信号的初始特征，能够很好地提取故障特征信息；魏文军等[6]采用EEMD 多尺度样本熵提取特征对S700K 转辙机进行故障诊断，通过EEMD 分解提取转辙机不同状态下的特征参数并进行聚类分析，验证了该方法对故障诊断的精度和效率有明显的提高。

通过EEMD 分解提取到的减速箱故障特征维数较高，会导致故障诊断效率降低，故选取PCA 法对故障特征降维。PCA 能较好融合减速箱的多个典型故障特征，将高维故障特征集映射到低维空间中，减少特征参数信息冗余[7]。故障特征参数的提取和选择是机器诊断的关键，而状态识别则是诊断的核心。FCM 算法作为一种无监督学习算法，可以根据特征参数样本的相似性进行分类，使处于同一类的相似度最大，并保证不同类间的差异性较大[8]。王印松等[9]将FCM 应用在控制系统的故障诊断中，不仅可以较好地识别不同部件的故障，还可以对同一部件不同类型的故障进行诊断。樊红卫等[10]针对电主轴转子不平衡故障，提出一种对称极坐标图像和FCM 相结合的失衡故障诊断方法，结果显示具有较高的分类准确率。

本文结合EEMD 分解和PCA-FCM 聚类算法对岸桥减速箱进行故障诊断。首先，将减速箱振动信号进行EEMD 分解并提取故障特征，然后利用PCA 对高维特征参数进行约简，最后使用FCM 算法对减速箱的状态进行聚类，并通过实验分析验证了该方法的有效性。

1 集合经验模态分解

EEMD 分解是对经典EMD 分解[3]方法的改进，该方法通过在原始信号中加入均值为0、标准差为常数的高斯白噪声，并对处理后的信号进行多次EMD 分解，取分解后IMF 分量的均值作为最终结果[4]。EEMD 算法的具体实施步骤如下：

(1)确定所加入的高斯白噪声比值系数α 和总体平均次数M。

(2)在原始信号x(t)中加入均值为零、幅值为原始信号标准差α 倍的高斯白噪声pi(t)：

式中，xi(t)为第i 次加入高斯白噪声后的信号。

(3)对xi(t)进行EMD 分解，得到k 个IMF 分量cij(t)和1 个余项ri(t)，如式(2)所示：

式中，cij(t)为第i 次加入高斯白噪声的信号分解后的第j个IMF 分量，ri(t)表示第i 次分解的余项。

(4)重复步骤(2)和(3)M 次，将上述步骤所得对应IMF 分量进行总体平均，以消除高斯白噪声对真实IMF分量的影响，得到最终IMF 分量为cj(t)：

(5)原始信号x(t)经过EEMD 分解的最终结果为：

式中，r(t)为原始信号x(t)经EEMD 分解后的余项。

2 故障特征的主成分分析

PCA 方法在有效降低原始特征集维数的同时，也可以很好地解释各个故障特征集与减速箱状态的相关性，特征系数表示各个原始特征参数在主成分中所占的权重，数值的大小表示对应故障特征在每个主成分中所占的比例[11]。系数值越大，说明对应编号的故障特征对于该主成分的贡献越大，利用该方法可以提取出减速箱更为敏感的故障特征参数。其具体实施步骤如下[7，12]：

(1)标准化处理，将故障特征矩阵转换成均值为0、方差为1 的标准化矩阵；

(2)计算相关系数矩阵；

(3)求故障特征矩阵的特征值和特征向量；

(4)计算累积贡献率；

(5)计算主成分得分。

3 模糊C-均值聚类算法

FCM 算法是一种基于目标函数迭代优化的聚类算法，可以用隶属度矩阵表示样本中每个数据点属于某一类的程度[8，13]。已知聚类特征参数样本X=[x1，x2，…，xn]的隶属度矩阵以及聚类中心，要使得特征参数样本数据非相似性指标的目标函数达到最小[8]。利用该方法对减速箱状态进行识别的基本步骤如下所示：

(1)根据减速箱故障特征参数的种类确定聚类中心的个数和模糊加权指数m，初始化隶属度矩阵U，设置初始迭代次数为l=0。

(2)根据目标函数确定特征参数样本数据的聚类中心C：

式中，U 为减速箱故障特征的模糊隶属度矩阵，uij∈[0，1]且；C=[c1，…，cc]；dij表示第i 组的聚类中心与第j 个故障特征间的欧氏距离；m 是一个加权指数且m∈[1，∞)。

(3)通过引入拉格朗日乘子λj(j=1，2，…，n)，计算目标函数值最小时的隶属度和聚类中心，uij和ci的更新公式分别如式(6)和(7)所示：

式中，dij和dkj分别代表不同故障特征到同一聚类中心的欧式聚类。

(4)对于设置的判别精度ε＞0，若||Ul+1-Ul||＜ε，则停止迭代；否则，令l=l+1，返回步骤(2)中继续执行，直到满足条件为止。图1 为减速箱故障诊断的流程图。

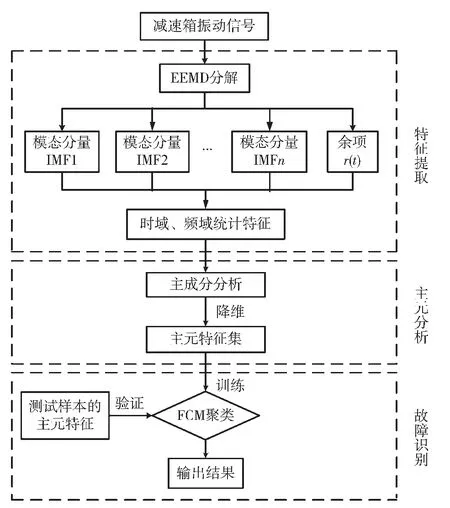
图1 减速箱故障诊断流程图

4 实验分析

4.1 减速箱振动信号采集

为了说明本文方法对减速箱故障诊断的有效性，采用岸桥减速箱不同状态下的振动信号进行验证。数据来自于宁波港某集装箱码头的岸桥减速箱，振动信号通过B608A11 型ICP 加速度传感器采集得到，传感器安装于起升电机减速箱的低速轴径向位置，如图2 所示。设置采样频率为2.4 kHz，采样时间为1 s，采样间隔为10 s，数据采集单元(Data Measurement Unit，DMU)计算并存储采样时段的有效值序列，获取减速箱振动信号时间序列。

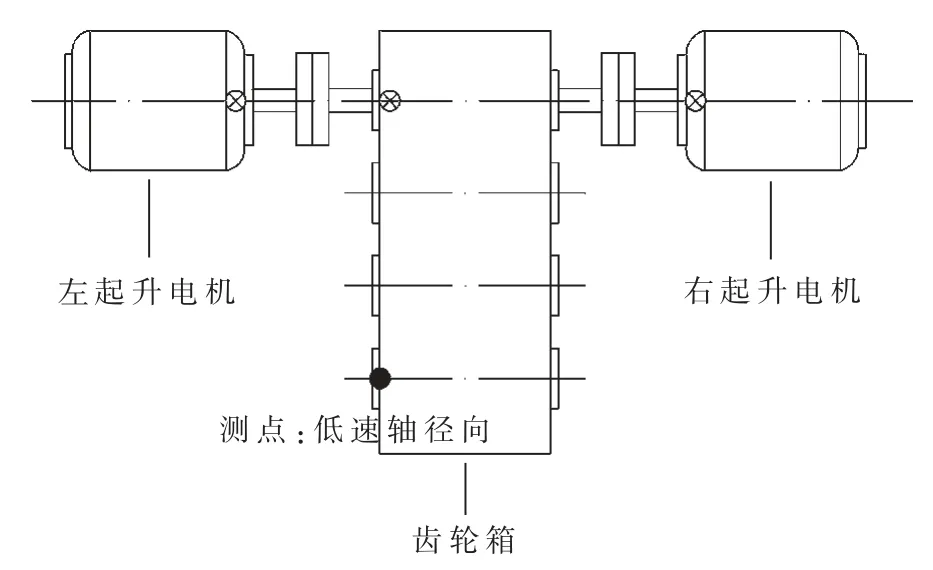
图2 减速箱传感器测点布置图

岸桥在非工作状态时的振动信号会影响故障诊断的结果，需要剔除该部分数据。直观上可以根据岸桥大梁的俯仰角度来判断，当大梁仰起时属于非工作状态；但有时当大梁位于水平位置时岸桥也可能处于非工作状态，则需要用振动信号的幅值来区分，当振动信号的波动整体非常小，且其中夹杂着一些大的波动，则判定为大梁水平时的非工作状态。非工作状态下减速箱振动信号被剔除前后的时域图如图3 所示，图3(a)、图3(b)和3(c)显示了减速箱3 种状态下的振动信号，分别为健康、亚健康以及预警状态；图3(d)、图3(e)和图3(f)分别显示去除非工作状态后3 种状态下的振动信号。不同状态下振动信号的幅值（振动烈度）具有较明显的差别，但由于岸桥吊装作业时的瞬间启停也会产生较大冲击，较容易对故障诊断的结果产生干扰，因此需要先进行故障特征提取。

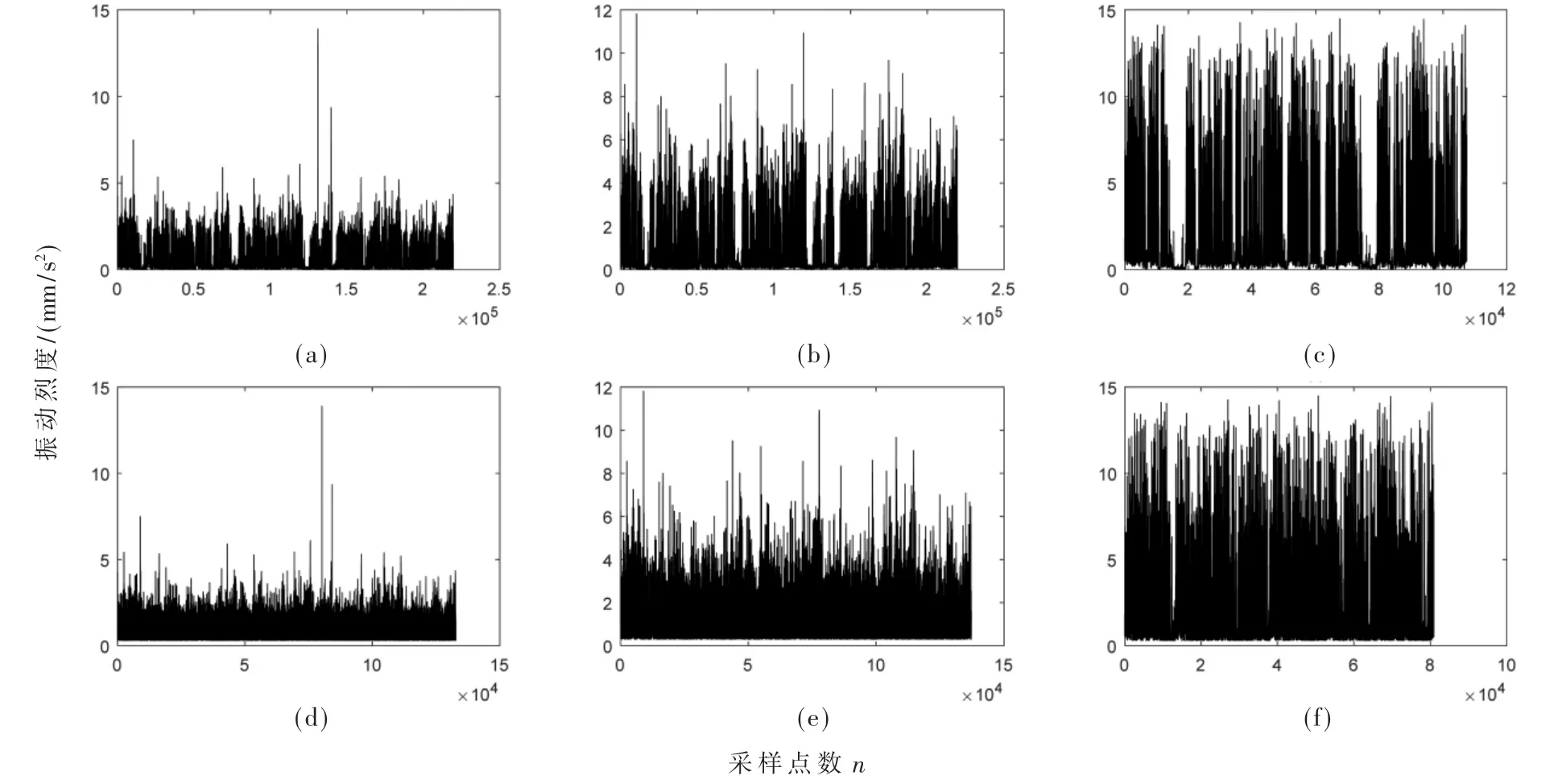
图3 减速箱振动信号时域图

4.2 特征提取与主成分分析

EEMD 分解处理减速箱非线性、非平稳振动信号具有较大优势[14]。本文采用文献[15]中的方法确定加入高斯白噪声的比值系数α，计算准则为：0＜α＜σ/2；α=εn/ε0；σ=εh/ε0。其中：εn为加入高斯白噪声幅值的标准差；ε0为减速箱振动信号幅值的标准差；εh为减速箱振动信号有效高频成分的幅值标准差；α 取值为σ/4 能有效避免信号分解时的模式混叠现象。总体平均次数M 与比值系数的关系为：。其中：e 为期望误差，一般取值为0.01。按照上述方法计算得到α=0.16，M=256，经过EEMD 分解得到不同状态下减速箱振动信号的各IMF 分量，限于文章篇幅，本文仅展示减速箱在健康状态下振动信号的EEMD 分解图，如图4 所示。

选取减速箱在健康和亚健康状态下的样本各80组，预警状态样本40 组，通过EEMD 分解提取每个样本的IMF1-IMF8 分量，分别计算每个IMF 分量的9 个统计特征值，即从每个样本中能提取72 维特征向量，得到200×72 维特征参数矩阵，具体计算方式见表1 所示。其中，xi为IMF 分量值，μx为xi均值。偏态指标对减速箱的状态变化较敏感，当发生局部故障时，减速箱的振动信号会明显偏离正态分布；此外，峭度指标和脉冲指标等特征参数对减速箱的早期故障有较高的敏感性，能很好地反映减速箱的初始状态。为了得到更多的减速箱故障信息，通过提取不同的特征参数，将它们综合应用以兼顾对减速箱的不同故障敏感性和稳定性的需求[4-5]。

表1 减速箱故障特征参数表

将减速箱故障特征矩阵进行归一化处理，然后对处理后的故障特征进行主成分分析，得到减速箱在一起不同状态下各个特征参数的主成分得分以及降维后的主元个数等，减速箱72 维故障特征数据的主成分贡献率矩阵如表2 所示。

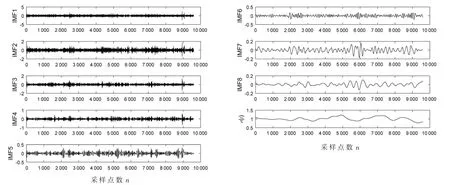
图4 减速箱振动信号EEMD 分解结果

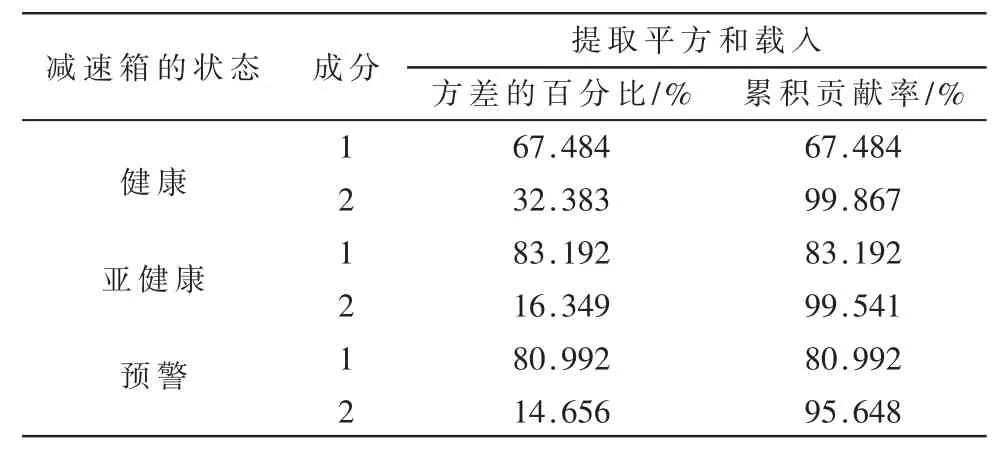
表2 减速箱特征参数主成分贡献率矩阵

由第2 节计算出减速箱振动信号的前8 个主成分特征系数的分布图如图5 所示，左一小图为第1 个主成分特征系数分布图，右1 小图为第2 个主成分特征系数分布图，第3 个～6 个主成分同理依次排列。图中横坐标为故障特征的维数，每个主成分均由72 个故障特征组成，纵坐标为每个故障特征所占的比重。由图5 可知，只有少数几个特征值在主成分中所占比重较高，多数故障特征系数接近于0。例如，第1 个主成分中，系数编号27、36、45、54、63 故障特征所占比例最大，其分别对应每个IMF 分量的有效值、偏态指标、峭度指标、波形指标和峰值指标，因此认为第1 个主元是各个IMF 分量的有效值、偏态指标、峭度指标、波形指标和峰值指标按不同权重相加组合的量，其他主成分可以同理分析。通过主成分分析可以提取出更为敏感的故障特征参数，反向追踪每个主成分的构成，可以推测出其实际的物理意义，为减速箱振动信号的故障特征提取提供科学依据。

4.3 减速箱故障识别

设置FCM 聚类算法的基本参数：聚类中心个数c=3，模糊系数m=2，收敛精度ε≤1.0×10-5，迭代次数k=100，原点定为迭代起点。根据式(7)迭代计算并不断更新聚类中心，直至目标函数收敛为止。4 种方法的二维聚类结果如图6 所示。其中：图6(a)为减速箱振动信号通过PCA 和FCM 算法得到的二维聚类分布图，与图6(b)中的PCA-K-means 聚类效果对比，FCM 算法比K-means方法对减速箱状态识别的准确率更高，但聚类效果仍不太理想，每种状态的聚类簇分布较散，且不同状态的聚类簇存在部分交叉混叠；图6(c)为减速箱振动信号经EEMD 分解，再通过PCA-FCM 算法得到的二维聚类分布图，和图6(d)中的K-means 算法都具有很好的聚类效果。这是由于EEMD 分解能较好地对减速箱的非平稳和非线性振动信号进行多分辨率分析和自适应分解，以便提取更多更准确的故障特征，达到提高岸桥减速箱故障识别准确率的目的。

为了评判FCM 算法识别的准确性，统计4 种方法对减速箱不同状态样本的识别情况。分别计算不同方法对减速箱不同状态识别的准确率，如表3 所示。通过对比PCA+FCM 方法和PCA+K-means 方法的识别结果可知，FCM 方法的识别准确率要高于K-means，说明FCM 聚类算法对减速箱的状态识别比K-means 算法更优；EEMD-PCA-FCM 方法和EEMD-PCA-K-means 方法对减速箱的状态识别准确率都高达100%，充分体现了EEMD 分解在减速箱特征提取上的较大优势。

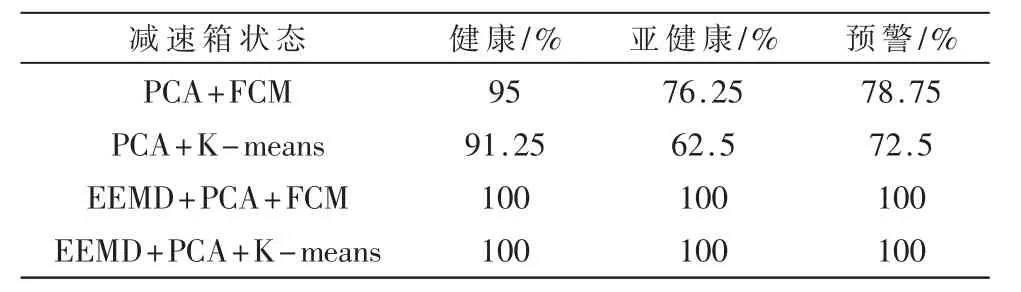
表3 4 种方法对减速箱故障识别准确率对比

5 结论

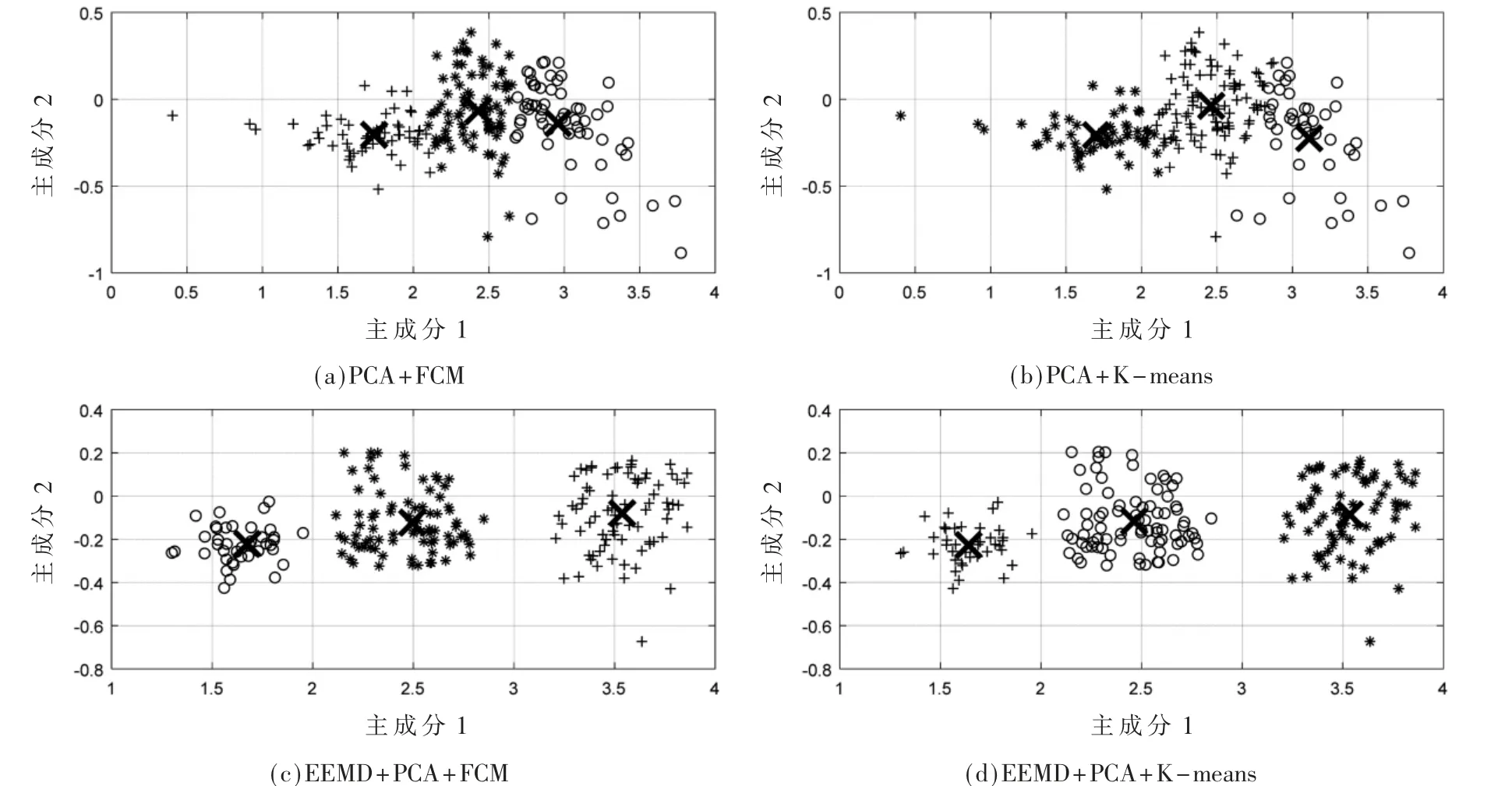
图6 二维聚类效果图

本文首先通过EEMD 分解得到减速箱振动信号的IMF 分量，得到振动信号在不同时间尺度下的特征参数，能够更加有效地提取减速箱的故障特征，使得减速箱故障诊断的精度和效率更高。其次，使用主成分分析法融合多个典型故障特征参数进行数据降维，减少无关或冗余特征向量，并分析了减速箱振动信号故障特征值与故障模式之间的联系。最后，利用FCM 算法对提取的主成分矩阵进行聚类分析，得到聚类中心后对减速箱振动信号样本进行状态识别和故障诊断。实验结果表明，将EEMD 分解和PCA-FCM 方法相结合能有效提高减速箱故障识别的准确率。