雪灾背景下的道路积雪清运线路优化问题研究
高杉
(四川大学 灾后重建与管理学院,四川 成都610207)
1 概述
雪灾是指强降温和大风伴随降雪或大风卷起地面积雪的天气,对道路交通和城市居民生活危害极大。我国北方冬季降雪频繁,当连续降雪,雪情超出预期时,相关单位需及时清除道路积雪,从而保障城市交通的有序恢复。
本文从路面积雪运输的角度出发,主要研究在给定服务区域,单车辆的弧路径问题优化问题。关于如何应对冬季降雪天气灾害,目前学术界的关注点主要是“硬工程”,而不注重“软优化”。如融雪剂的研发、扫雪车的改进、城市道路规划,鲜有管理方向上的讨论与研究。显然,管理科学能够帮助有关部门在一定程度上合理安排清扫车辆的运行线路,帮助提高现有资源的利用水平。
弧路径问题是路径优化问题最重要的类别之一,主要包括中国邮递员问题、乡村邮递员问题和容量约束弧路径问题(Capacitated Arc Routing Problem, CARP)[1]三大类。CARP 由Golden 和 Wong (1981)[2]提出, 作者同时证明了 CARP 是NP-hard 问题。对于这类问题,在解决大规模应用实例时,通常不选用精确解算法,而是采用近似解算法。Liu 等人[3]对求解CARP 的近似解算法进行了回顾。
蚁群算法是最热门的仿生优化算法之一,在NP-hard 问题的求解过程中被不断改进、创新。在容量约束弧路径问题的研究上,Lacomme 等人(2004)[4]提出了蚁群优化算法求解CARP 问题。Santos 等人(2010)[5]对蚁群算法的初始种群、蚂蚁决策规则和局域搜索程序进行了修改,更好地求解CARP 问题。
2 数学模型
积雪清运车辆路径问题可描述为:某清运车辆从场站出发,对其作业区域内需求边进行服务,当服务过某些需求边车辆满载后,需行驶至指定的消纳场倾倒积雪,完成后接着行驶,服务未服务的需求边,直至该区域内所有需求边都得到服务,车辆返回车场,此为该车辆行驶的整个路径。问题就是事先确定该车的行车路径,在一定约束条件下,实现距离成本最小(也就是时间成本最小)的目标。


该问题基于以下假设:
(1)求解车辆的作业区域已经划定;
(2)各边的距离成本、需求量已知;
(3)消纳场的容量不限。
模型中涉及的参数及变量定义如表1 所示。
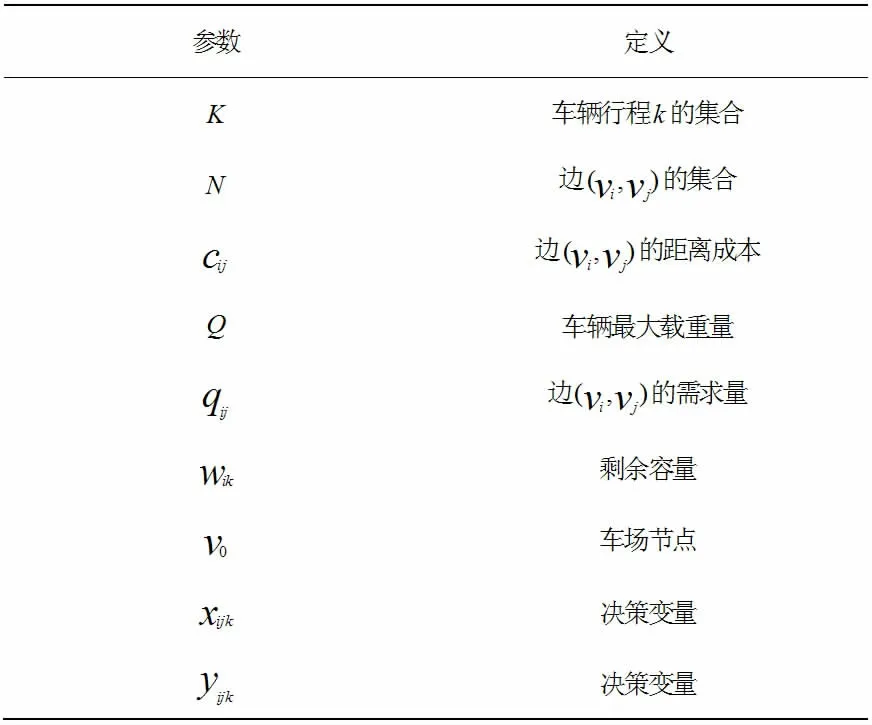
表1 参数及变量定义
目标函数和约束条件如下:
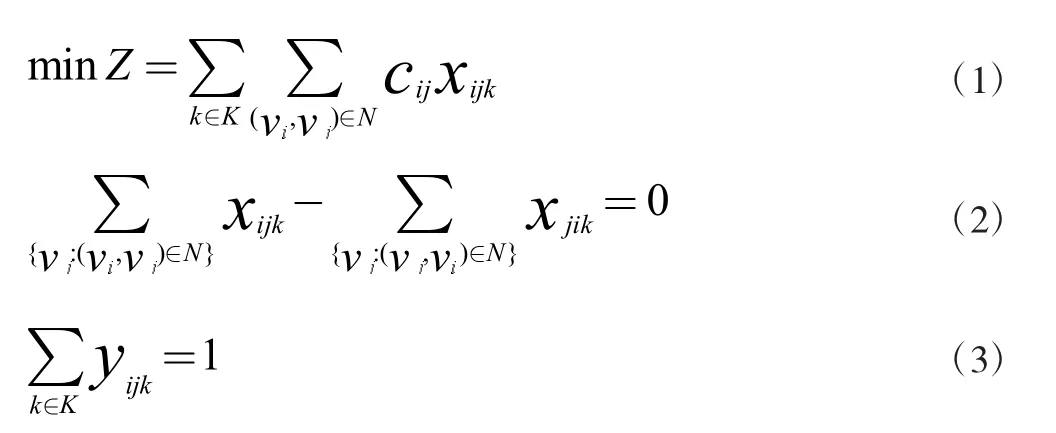

目标函数(1)表示积雪清运车辆路线的总距离成本最小。式(2)表示车辆从Vi进,也要从Vi出。式(3)表示需求边必须被服务一次。式(4)表示每条边的访问次数不能小于其被服务的次数。式(5)表示每个行程的容量限制。式(6)表示如果车辆经过边(Vi,Vj),那么离开Vj时的剩余容量等于进入Vi时的剩余容量减去边(Vi,Vj)的需求量。式(7)表示整条路线,车辆从车场出发一次。式(8)表示整条路线,车辆最后回到车场。式(9)表示清运车辆的最后一次行程必须空载返回车场。式(10)和(11)表示消除子回路。式(12)和(13)表示决策变量的取值范围。
3 算法设计
本文的求解算法针对道路积雪清运路径优化问题,基于蚁群算法,进行了以下算法的设计:

第八步,判断是否达到最大迭代次数NCmax;
第九步,输出结果。
算法流程图如图1 所示。
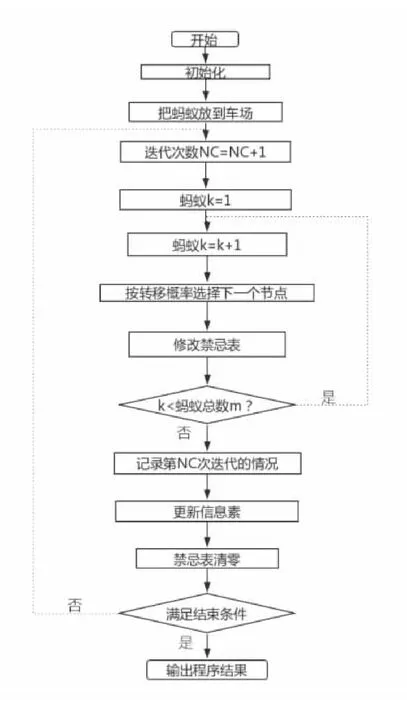
图1 蚁群算法求解积雪清运线路优化问题流程图
4 算例实验以及分析
4.1 算例和参数设置

由于蚁群算法是典型的概率算法,所以算法中的参数通常需要由实验确定。但参数设计不是本文研究重点,所有直接采用以往文献给出的参考规则。这些规则包括:
(1)节点数量约为蚂蚁数量的1.5 倍[7];
(2)α 在1 附近,β 在5 附近,ρ 在0.7 左右[8];
(3)常数Q 对算法的性能没有明显的影响[9];
(4)α、β、ρ 的大小与最大迭代次数呈负相关,最大迭代次数不宜过大或过小[10]。
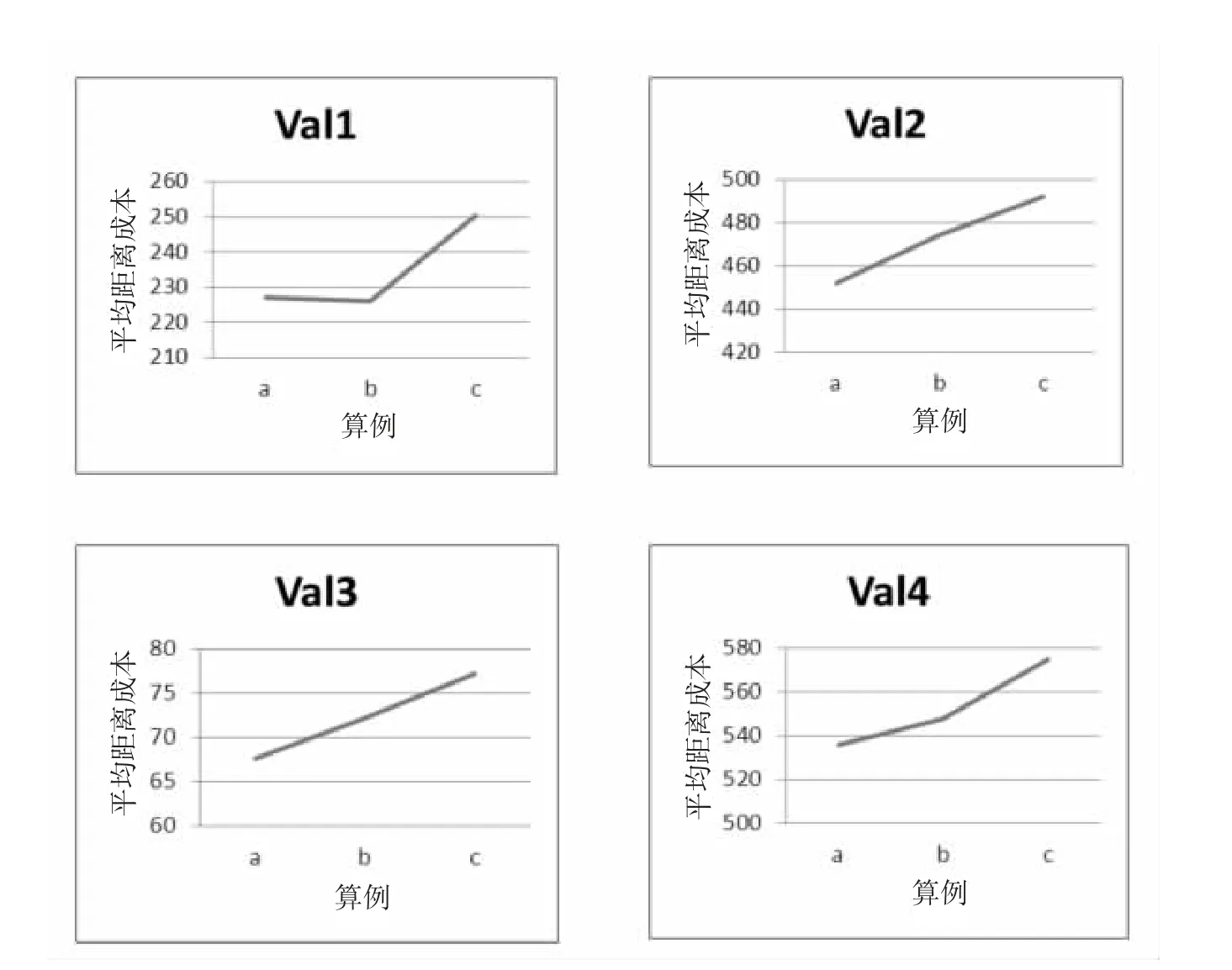
图2 距离成本与车辆最大载重量关系折线图
因此,以上算法参数取值分别定为:m=30;α=1;β=5;ρ=0.7;Q=1;NCmax=100。
4.2 实验结果
计算结果如表2 所示。
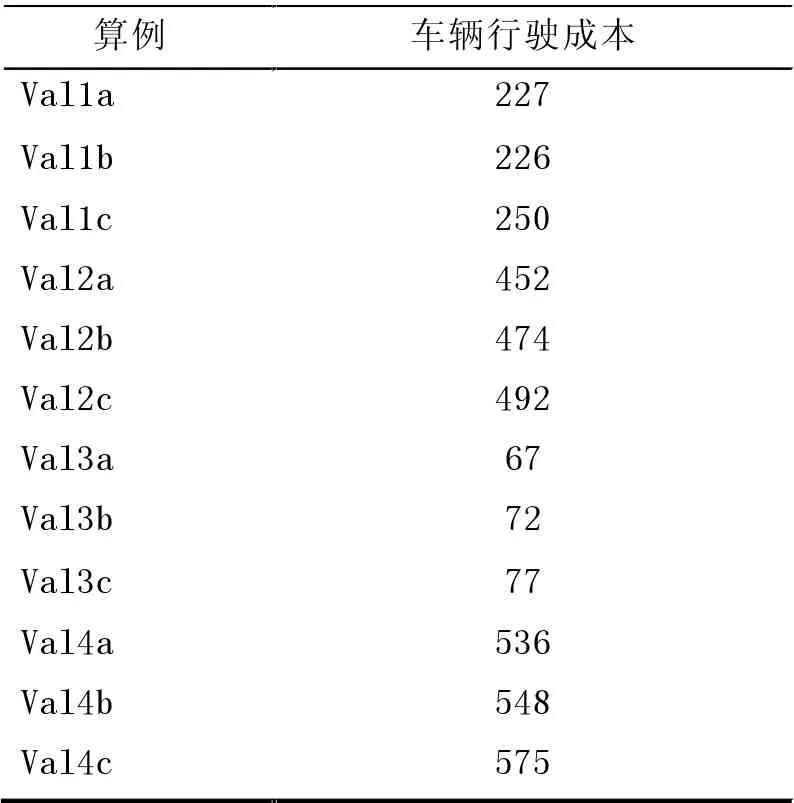
表2 算例结果
在四组算例中,每组算例的车辆最大载重量作为变量递减,将该四组的距离成本和Q 的关系用图2 分别表示,可以看,出当车辆容量越小时,行驶的总成本越高,这是因为容量小意味着容易装满,所有前往消纳场的次数也就越多,空跑的比重也会增大。
5 结论
本文研究了路面积雪清除线路优化的问题,设计了相应的弧路径优化模型和蚁群算法进行求解。在大范围内对车辆路径进行理论化求解,可以辅助人工作业,弥补经验偏差,使得工作更有效率。
本文也有很大的改进空间。本文仅仅是针对车辆服务区域划分完后区域内单车辆弧路径规划,之后的研究有必要将区域划分理论与该研究结合,从更大的整体上优化弧路径问题,同时,多车辆、多车型、需求可拆分、道路限制等方面都是延伸的重点。

