基于乘客到站率的公交发车频率优化

李悦超，杨海飞，郑长江

（河海大学土木与交通学院，江苏 南京210098）

随着我国城镇化建设的推进，城市的人口和机动车保有量迅速增加，城市发展普遍面临着严峻的交通拥堵问题。 为减轻城市道路设施负载，政府积极鼓励和引导乘客利用城市公共交通出行。 常规公共汽车作为城市公共交通工具中最重要的出行方式之一，可有效改善城市居民出行结构，提高出行效率。 公交在运营调度时，公交时刻表是关键，而发车频率又是公交时刻表的核心内容， 若能制定科学、合理的公交发车频率，使其在满足城市日常客流需求的同时，能够充分利用公交资源，有利于实现社会效益的最大化。

公交发车频率建模的研究可以追溯至上世纪八十年代。1984 年，Ceder[1]基于客流数据调查，提出了发车频率的4 种确定方法。 方法分别从线路的日最大断面客流、站点最大断面客流、公交载客里程以及载客里程基础上保证服务水平的改进4 个角度得出。 该发车频率确定方法简便有效，为后续研究提供了借鉴与参考。

目前， 已有研究主要从两个角度考虑优化公交发车频率：一是从乘客成本（效益）角度来构建模型。 这类建模方法的核心是在发车频率优化模型中以乘客乘车和等待时间最小为目标[2-4]。 在此基础上，部分研究进一步深入，考虑了交叉口延误时间[5]、乘客换乘时间[6]、车内拥挤情况[7]等因素。然而，以上研究对公交运营成本的关注较为欠缺，主要通过设置车队规模上限的方式确定公交运营的投入上限，而未考虑如公司运营成本、车队成本等因素的具体影响。 二是从社会成本（效益）角度来构建模型。 例如Wihartiko 等[8]以最大化公交收益同时减少公交成本为目标建立模型；Shashi[9]的发车频率模型考虑了乘客等待时间和运营成本；张东等[10]针对BRT 公交的特点，考虑乘客与公交公司两方面建立发车频率模型。 上述模型考虑了社会的整体效益， 在考虑公交服务水平的同时也注重合理利用公交资源，提高公交载客率。 但在此类研究中，在考虑乘客等车时间这一指标时，对相关影响因素的考虑不够充分， 导致模型与实际等车时间有一定的误差。

针对现有研究存在的局限性，文中提出以乘客和公交运营的总成本最小为目标建立发车频率优化模型，模型考虑乘客的等车时间成本和车内拥挤成本， 以及公交运营中的车辆购置成本和燃油成本，优化发车频率以降低总成本。 另外，该模型针对乘客等车时间的计算误差问题，引入乘客到站率这一动态因素，建立乘客到站函数，使得模型在优化计算中具有更符合实际情况的乘客等车时间。 在实际应用中，大规模的乘客和站点数量会增大发车频率模型的求解难度和计算效率。 考虑到启发式算法在求解复杂组合优化问题时具有良好的鲁棒性和收敛性，文中设计遗传算法对所建立的多目标优化模型进行求解。 文中综合考虑乘客和公交公司的对发车频率的需求，能为公交发车频率的制定提供更加全面的决策支持。

1 优化模型

文中发车频率的优化考虑乘客与公交公司两方面的因素， 其中乘客期望获得更加舒适的服务（包括减少等车时间、减少车内拥挤情况），而公交公司期望减少其运营成本。 模型的建立应兼顾受发车频率影响的乘客成本和公交运营成本，才能使其整体的成本降至最小。 文中将分别对乘客成本和公交运营成本建模，并以总成本最小构建发车频率优化模型。

1.1 模型假设

将全天的公交运营时间分成若干时间段，文中主要研究在特定时段内，单一公交线路的运行车辆从首站至末站的单向行驶过程， 共分为m 个站台。将该线路首班车从起点出发至末班车到达终点的时间段作为运营时间，运营时间可依据客流特征将其划分为个时间段，如分为早高峰、晚高峰、平峰段3 个时间段。 针对不同时间段分别设置合理的发车频率，使该时间段内的总成本达到最小。

在构建模型前需要对实际问题进行概括，对模型进行如下假设：

1） 本次模型仅考虑单一公交运行线路，且不受其他线路的影响；

2） 公交公司提供统一的车辆型号，车辆间座位数、载客数一致；

3） 公交车在运行过程中匀速行驶，不考虑突发事故等情况；

4） 同一线路公交车运行中不考虑公交串车；

5） 乘客在公交站台排队上车，服从先到先服务的原则；

6） 公交运行过程中不考虑乘客滞留；

7） 根据客流量在不同时段选用不同的发车频率，且同一时间段内，发车频率保持不变。

1.2 乘客到站率

利用乘客到站率这一动态因素，构建乘客到站函数，借此可以计算每个站台的乘客等车时间。 乘客到站率是指在某个时段内，到达公交站点的乘客数量。乘客到站这一情景属于相互独立、互不干扰的事件， 已有研究指出乘客到达站台服从泊松分布[11]。可以用乘客到站率计算某一线路的某一公交车站，在一段时间内达到的乘客的数量。

首先， 基于以上理论推导出t 时间段内到达n个乘客的概率为

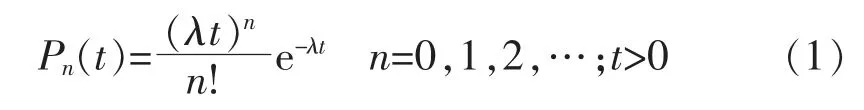
式中：Pn（t）为时间段内到达n 个乘客的概率；λ 为乘客到站率；n 为到达公交站的乘客数量；t 为到达n 个乘客的时间。

借此可以得到，每个乘客到达公交站台的间隔时间t 服从负指数分布。 即乘客到达站台的概率密度函数如下

式中λij即为j 时段内第i 个站点的乘客到站率。

综上， 可以对j 时段内第i 个站点的乘客的等车时间进行计算，以乘客等待一班车为例，计算公式如下

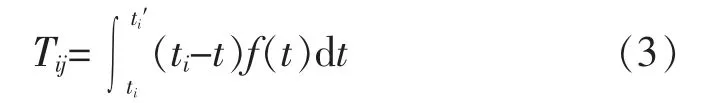
式中：Tij表示在j 时间段内站点i 的所有乘客等待一班车所花费的时间；f（t）表示j 时段内站点i 乘客到达站台的概率密度函数；t 为本班车的到站时间；ti′为上一班车的到站时间， 通过积分得到该站台乘客等待本班车所花费的总时间。

1.3 乘客成本建模

乘客在乘车出行的过程中，对时间和车内拥挤情况最为敏感。 考虑行程时间中等车时间与发车频率关系密切，文中将乘客成本分为乘客在公交站台等车的时间成本与车内拥挤成本D。 以j 时间段内一次发车为例， 第i 站上车的乘客的等车时间成本计算公式为

式中：Tij为j 时间段内站点i 的所有乘客等待一班车所花费的时间， 通过前文的乘客到站率函数算出；α 为乘客的时间价值，由所在城市的人均工资折算而来。

式中fj为j 时间段内的发车频率。

1.4 公交运营成本建模

考虑到公交运营中公交车辆购置与车辆行驶里程与发车频率关联密切且便于量化，文中将公交运营成本分为由车辆购置带来的成本和由车辆行驶里程增加而带来的燃油成本。 其中车辆购置成本U 具体公式如下

式中：η 为车辆每公里的燃料成本；L 为线路的总行驶距离；fj为j 时段内的发车频率。

结合以上分析，公交运营成本Ce为

1.5 发车频率优化模型

为使得模型的建立兼顾乘客和公交运营的利益， 规划目标为乘客成本Cc和公交运营成本Ce之和最小。 将前文乘客成本、公交运营成本公式相结合，建立如下发车频率数学模型

约束条件反映了公交的发车频率必须满足公交的基本服务水平需求，即发车频率需高于公交最小发车频率， 同时应考虑公交企业的运能上限，即低于规定的最大发车频率。文中取最大发车频率fmax为40 次/h，最小发车频率fmin为4 次/h；β 为车内拥挤的惩罚因子，拥挤程度越高，惩罚因子越大，其值需满足非负性。

1.6 模型求解算法

考虑遗传算法对具有较强的鲁棒性和较快的收敛速度，文中使用遗传算法对模型进行求解。 遗传算法关键步骤包括编码、适应度函数、遗传过程（选择、交差、变异）。 发车频率的数据格式易于进行二进制编码，适用于遗传算法的求解，这也是文中选择遗传算法的原因之一。 在遗传算法中，适应度通常用来反映解的优劣，文中以目标函数作为适应度函数，即对应解的总成本越小，则适应度越高，其特征保留至下一代的概率越高。 遗传过程的选择、交叉、变异分别使用经典的赌轮盘法、单点交叉法、设定变异率来确定。

文中具体算法步骤如下：

步骤1：确定编码形式（二进制编码）以及参数；

步骤2：生成初始解，在发车频率范围内随机生成规定个数的个体，它们代表不同发车频率，并将其二进制化；

步骤3：根据问题确定适应度函数，本研究将公交乘客和公交运营总成本作为适应度函数，总成本最小为最优；

步骤4：计算每个个体的适应度值，并排序；

步骤5：遗传过程，包括选择、交叉、变异，分别采用赌轮盘法、单点交叉法、设定变异率来确定，得到新的种群；

步骤6：对种群扩充，恢复到设定的个体数量；

步骤7：判断是否到达到最大迭代次数，如果达到，则转到步骤8，其他情况则迭代次数加一，转到步骤4；

步骤8：解码，输出结果。

算法将种群数目设置为40，确保其在覆盖发车频率范围的情况下运算速度尽可能快。 最大种群迭代数设置为100，确保在其迭代次数内求得最优解。二进制位设置为20，确保求得发车频率的精度。 选择概率，变异概率，交叉概率分别设置为0.9，0.1，0.5，保证遗传算法的收敛性。 具体遗传算法的参数如表1。

表1 遗传算法参数表Tab.1 Genetic algorithm parameters

2 实例分析

本节将分别运用文中提出的基于乘客到站率的多目标发车频率模型以及Ceder[1]提出的经典发车频率确定方法对实例进行计算求解，并对求解结果进行对比分析，证明文中提出模型的有效性和性能优势。

考虑到高峰时段交通拥堵问题严重以及乘客出行量的激增，此时乘客成本与公交运营成本之间的矛盾最为突出，且由于平峰时段的数据样本量较少，本文主要针对高峰时段的公交发车频率进行优化。

2.1 实例介绍

以常州市B1 路公交车的线路为例，B1 路一共存在30 个站点，首站为武进公交中心站，末站为常州北站，全站行驶距离为30.1 km。 通过交通调查，获得各站台在17:10—17:40 这一高峰时段的乘客到站率和下车率数据，以此计算此高峰时段的最优发车频率。

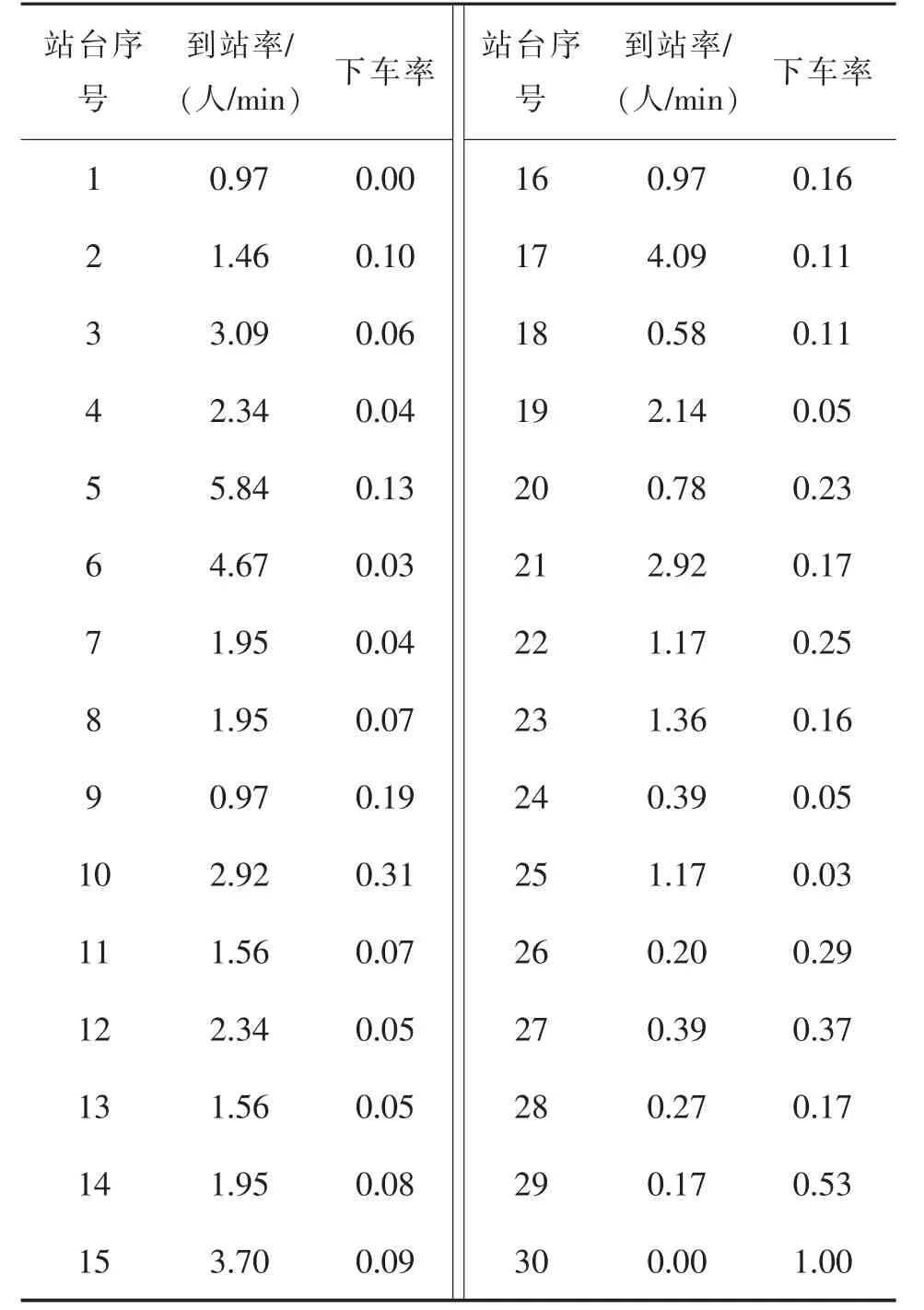
表2 17:10—17:40 各站台的乘客到站率和下车率Tab.2 Passenger arrival and drop-off rates at various platforms from 17: 10 to 17: 40

2.2 实例计算

首先利用基于乘客到站率的多目标发车频率模型和对应的求解方法计算该实例在17:10—17:40 这一高峰时段的最优发车频率。 将实例数据以及涉及的参数代入其中。 本实例涉及的各参数赋值见表2。

将表1 的数据代入模型， 并对发车频率求解，得出在17:10—17:40 这一高峰时段，最优发车频率为13.9 ，对应的发车间隔为4.3 min，此时总成本达到了最低518.2 元。 遗传算法迭代过程见图1。

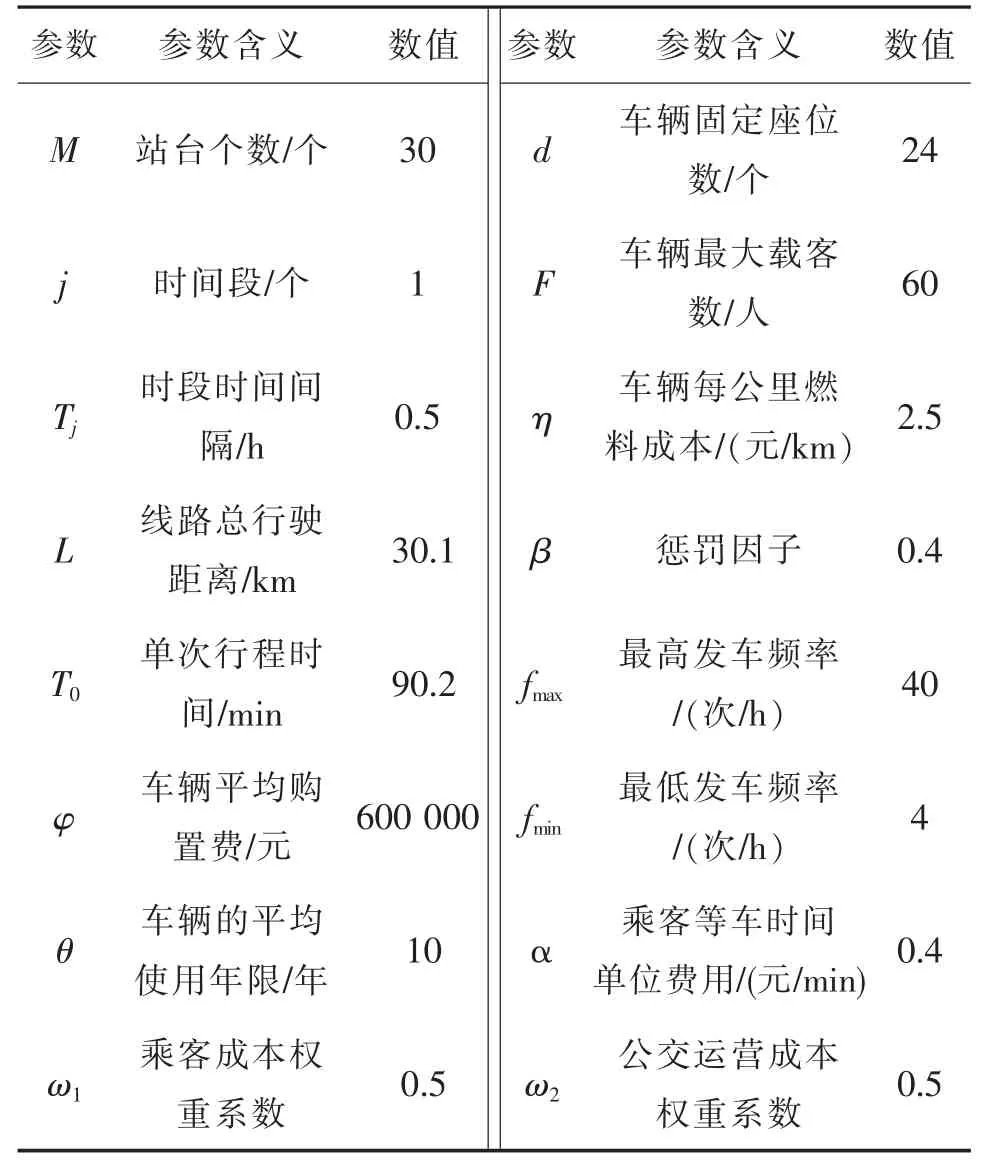
表3 模型参数值Tab.3 Model parameter value

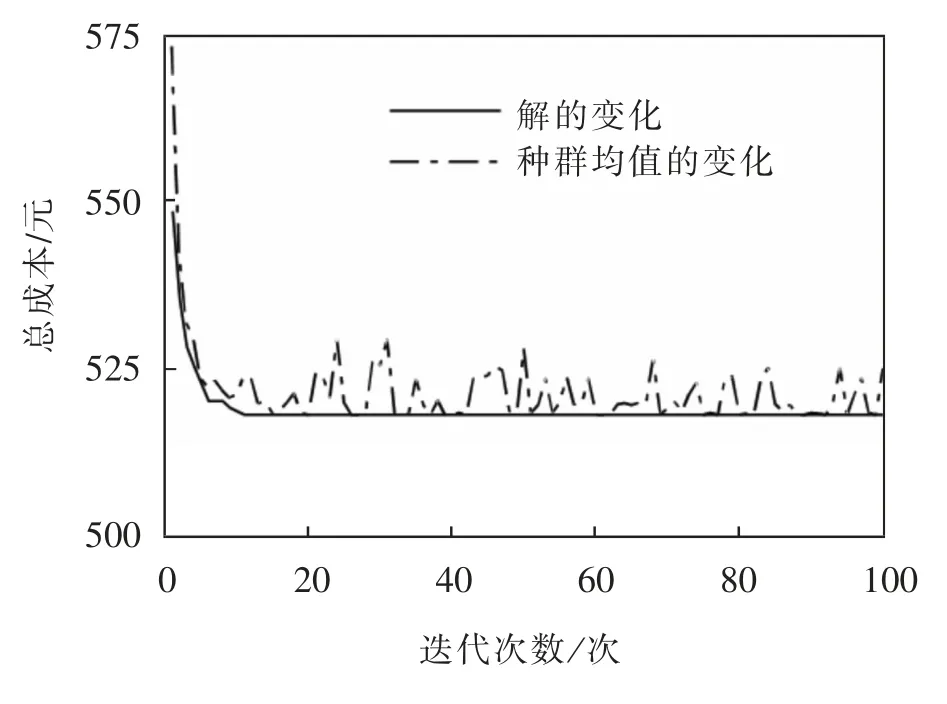
图1 遗传算法迭代图Fig.1 Genetic algorithm iteration diagram

运用Ceder[1]提出的3 种发车频率确定方法对该实例进行计算，将结果与文中提出的优化模型结果进行对比分析。 下面将3 种方法分别命名为方法一，方法二，方法三并进行介绍。

方法一是基于公交路线中的站点最大断面客流量确定发车频率，其计算表达式如下

式中：Fmj为j 时间段内规定的最小发车频率；Pmj为j时间段内车内乘客总数最大的站点；doj为j 时间段内公交车的预计载客率，doj=γjc；Pij为j 时间段内站点i 至下一站的车内乘客总数；γ 为车辆最大载客数；c 为满载率， 设为0.8， 表述预期的车内拥挤水平。

数据代入计算得F1=24.6 次/h。

方法二通过结合站点断面客流和载客公里数确定发车频率，其计算表达式如下

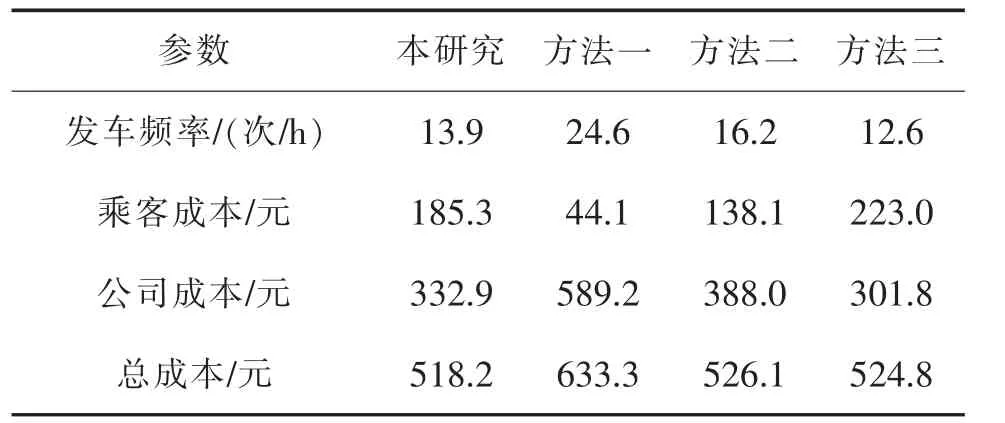
表4 各方案的成本对比表Tab.4 Cost comparison

式中：Aj为j 时间段内上车乘客总行驶距离，人/km；L 为公交线路长度，km；Fmj为j 时间段内规定的最小发车频率；doj为j 时间段内公交车的预计载客率，doj=γjc；为各站台平均断面流量；Pij为j 时间段内站点i 至下一站车内乘客数；li为站点i 至站点i+1的距离。

数据代入计算得F2=16.2 次/h。

方法三在方法二的基础上加入抑制车内拥挤的因子βj，其计算表达式如下

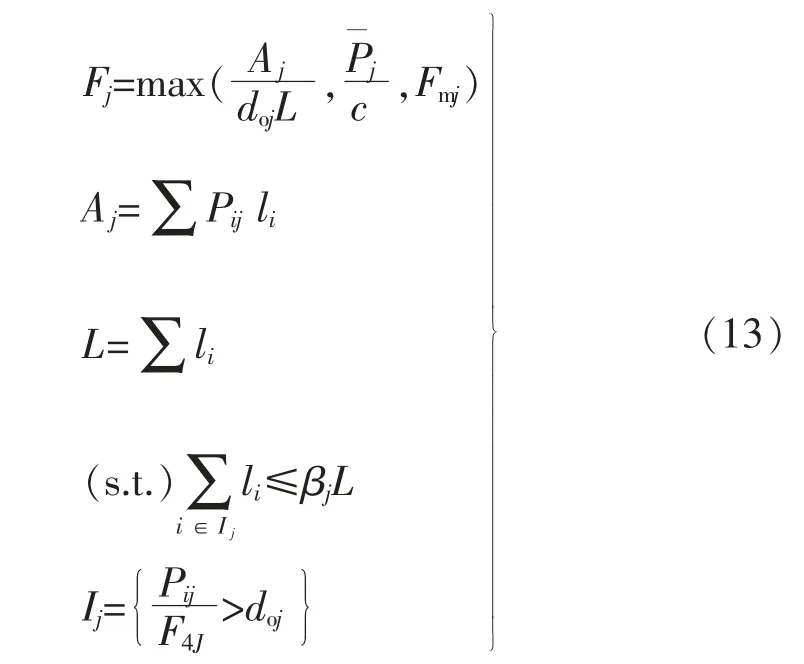
式中：Ij为j 时间段内断面客流高于公交服务水平的站点集合；βj为设定参数，βj=0.75。

数据代入计算得F3=12.6 次/h。

2.3 结果比对

将文中提出的发车频率优化模型和上文Ceder教授提出发车频率确定方法一，方法二，方法三。 计算实例的发车频率并带入到成本模型中，得到各方案的乘客成本、公交运营成本以及总成本。 各方案的成本对比如表4。

通过比较可以看出，本文中提出的优化模型的总成本相较于其他三种方法成本最低，为518.2 元，比其他三种方法分别降低了18.1 %，1.5 %，1.2 %。说明了模型在高峰时段降低总成本上的有效性。 由于总成本由乘客成本与公交运营成本组成，可以看到：方法一更多考虑了乘客的成本，提高了公交服务水平，但过高的发车频率也使得公交运营成本过高，影响了整体收益；而方法三则相反，主要减少了公交运营的成本，但乘客成本过高，影响乘客的出行感受；方法二的公交运营成本和乘客成本介于两者之间，但相较于文中提出的模型，并未达到最低成本。 可以看出，文中提出的优化模型得出的发车频率较好地平衡了两者之间的关系，使得高峰时段总成本达到了最低。 由于只针对高峰时段进行了分析，在后续的研究当中，通过进一步补充数据对平峰时段进行优化。

3 结论

文中提出了基于乘客到站率的发车频率优化模型，并且运用遗传算法进行了求解。 通过实例计算证明了模型在高峰时段降低乘客与公交运营的总成本的有效性。 本研究主要结论包括以下几个方面：

1） 提出基于乘客到站率的发车频率优化模型，模型考虑了乘客的等车时间成本、车内拥挤成本以及公交运营成本。 其中乘客的成本通过引入乘客的到站率函数来计算，通过协调乘客成本和公交运营成本来使得总成本最小。

2） 根据本研究的问题特点设计了相应的遗传算法，确定设计思路和具体步骤，对文中提出的公交发车频率优化模型进行求解。

3） 利用常州B1 路公交线路的实例数据，通过与经典发车频率确定方法的结果比较，验证了文中提出的模型在高峰时段降低乘客和运营总成本方面的显著效果。

综上，文中提出了基于乘客到站率的发车频率优化模型，通过考虑乘客成本和公交运营成本两方面，确定最优的发车频率，使得公交整体的总成本达到最低。 研究为公交发车频率的确定提供决策支持，利于促进公交进一步发挥社会效益。