椭圆速率驱动抽油泵工作行为分析*
段志刚 王志 廖显涛 储明来 司志梅 李伟 王辽
(1.中国石化江苏油田分公司石油工程技术研究院2.中国石化江苏油田分公司采油一厂 3.西南石油大学机电工程学院)
0 引 言
游梁式抽油系统作为非自喷采油的主要方式之一,在世界各地原油产区仍被广泛使用。但游梁式抽油机的常规运行与几何结构会使柱塞运行速度分布不均匀,存在大的速度峰值,在个别间歇出油井中,由于供液严重不足而导致憋泵现象发生的概率大大提高。鉴于此,提出了抽油机柔性运转控制技术。该技术是一种变速驱动技术,通过电机的变速运行来控制抽油系统,目的是改善工作进程、降低采油成本、提高采油效率。目前国内众多油田采用了抽油机柔性运转控制技术[1-4],学者们对该技术下电机参数、抽油机启动运行和三轴扭矩等方面进行了测试分析[5-8],但针对抽油泵方面的研究较少。为探究变速驱动对抽油泵的影响,笔者采用椭圆速率与常规速率进行对比,分析了2种驱动方式下抽油泵的漏失、泵效、阀球的开启以及流场等情况,以期为柔性运转控制策略提供一定的指导。
1 椭圆速率特征
椭圆速率的主要特征在于曲柄的每一个角度对应一个变化的角速度,在极坐标中构成椭圆形曲线,并且该椭圆形曲线在短半轴的角度时,抽油系统在上、下死点位置。椭圆速率与常规速率极坐标曲线如图1所示。
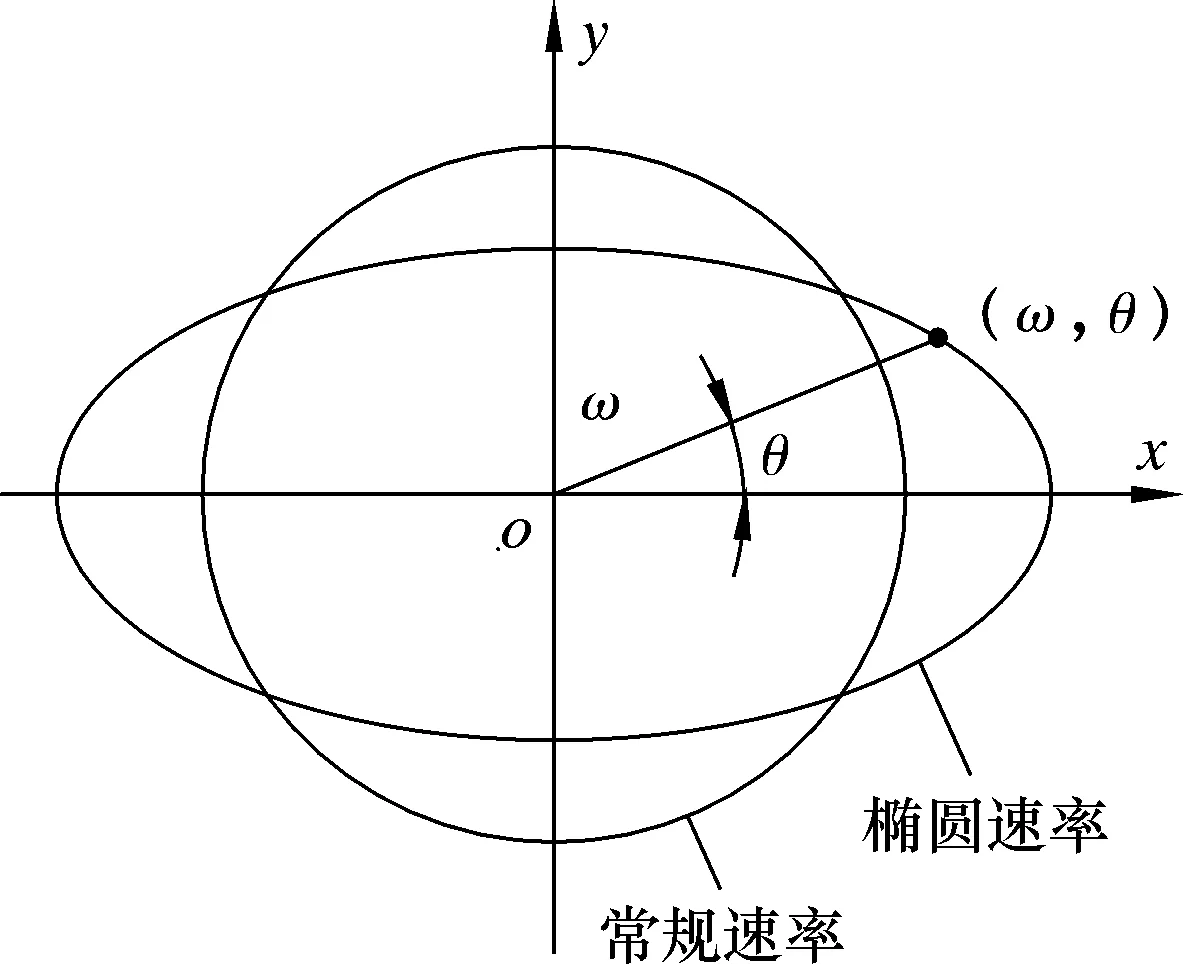
图1 椭圆速率与常规速率极坐标曲线图Fig.1 Polar curve of elliptical rate and conventional rate
2 漏失分析
对于抽油泵而言,椭圆速率仅改变了柱塞运动规律,主要影响抽油泵的漏失。
抽油泵通过柱塞的上、下运动来实现整个抽油过程,其工作原理如图2所示。抽油泵的漏失主要包括:①柱塞与泵筒之间的间隙漏失;②因静阀与动阀的滞后启闭导致的阀隙漏失。
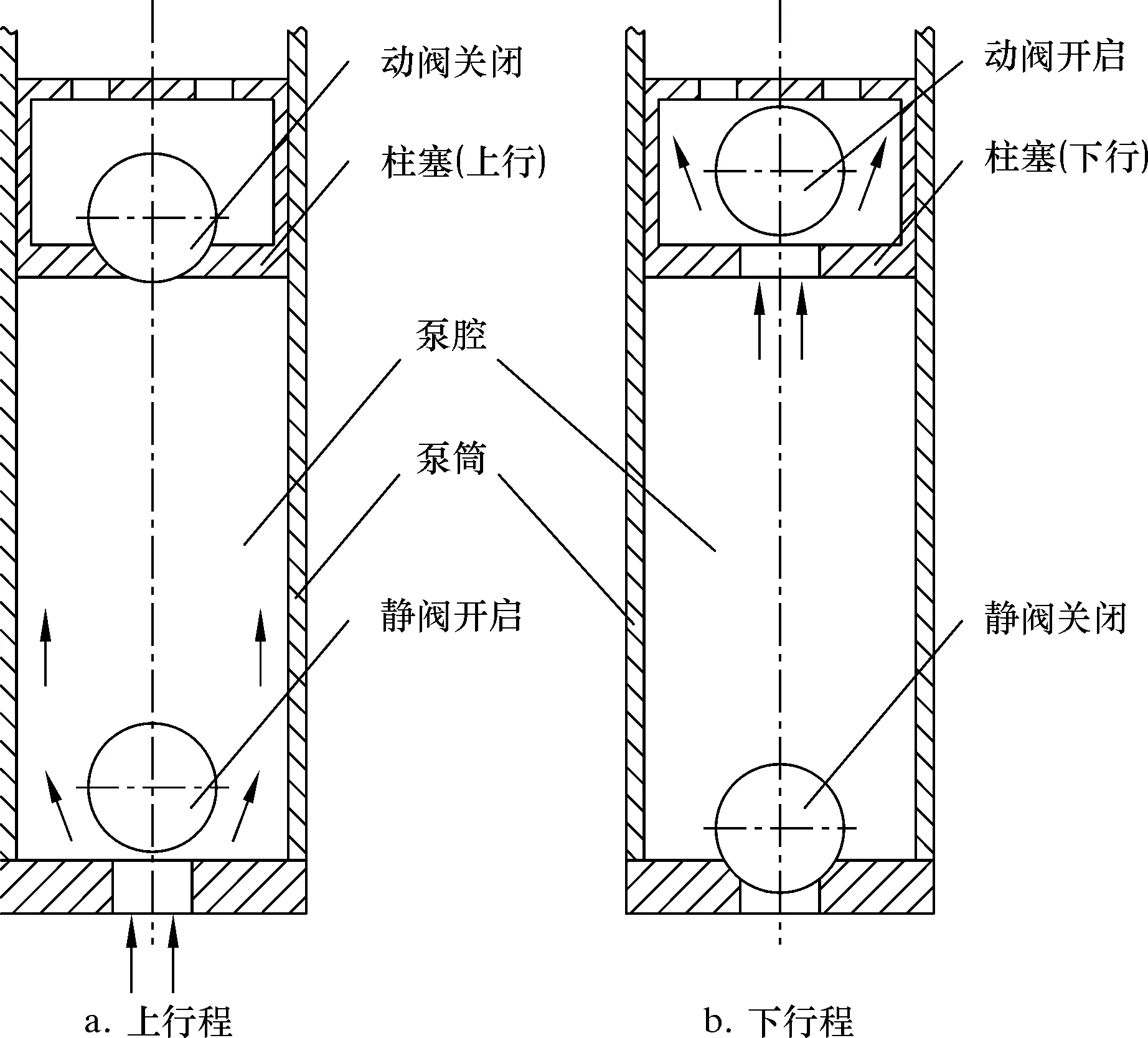
图2 抽油泵工作原理图Fig.2 Working principle of oil well pump
2.1 间隙漏失
柱塞与泵筒之间的间隙漏失量计算式为[9]:
(1)
式中:Q1为间隙漏失量,m3/s;D为柱塞直径,m;δ为间隙宽度,m;Δp为柱塞两端压差,Pa;μ为流体动力黏度,Pa·s;l为柱塞长度,m;e为偏心距,m;va为相对运动速度,m/s。
2.2 阀隙漏失
抽油泵泵阀的启闭是泵正常工作的重要前提。对静阀阀球运动做以下假设:①忽略因流体在泵筒内流动产生的摩阻损失;②泵筒内各点的流体压力和密度一致[10-12]。由质量守恒定律,单位时间内,泵筒内流体质量的增量应等于经过阀隙流进泵筒内的流体质量,则泵筒内流体的连续性方程为:

(2)
其中:

(3)
(4)

(5)
式中:p为泵筒内流体压力,Pa;υ为流量系数;ρxs为经过阀隙的流体密度,kg/m3;ps为泵吸入口压力,Pa;ρ为泵筒内流体密度,kg/m3;hs为阀球升程,m;Ap为泵筒截面积,m2;xp为柱塞位移,m;x0为防冲距,m;Vs为阀隙、阀球与阀座形成的体积,m3;fxs为静阀阀隙过流面积,m2;fvs为静阀阀球工作面积,m2;rsu为静阀阀座孔研合宽度的最大半径,m;Rs为静阀阀球半径,m。
假设阀球沿阀座中轴线做直线运动,由牛顿第二定律建立阀球运动微分方程,即有:
(6)
式中:g为重力加速度,m/s2;Ab为阀球投影截面积,m2;mb为阀球质量,kg;CD为绕球流动系数;vin为泵筒内流体速度,m/s。
以不完全研合式阀座结构研究阀球开启情况。忽略阀球惯性力的影响,静阀开启时压差与泵内压力为:
(7)
pos=ps-Δpos
(8)
式中:Δpos为静阀开启压差,Pa;d1为研合弧下端横截面的直径,mm;d2为研合弧上端横截面的直径,mm;pos为静阀开启时泵内压力,Pa。
以单相原油为流体介质,由质量守恒定律可得静阀开启时柱塞位移:
(9)
式中:xos为静阀开启时柱塞位移,m;Δxcd为动阀关闭时,柱塞由下死点往上运动的距离,m;ρpd、ρos分别表示泵内压力为排出压力ppd和开启压力pos时的流体密度,kg/m3。
由柱塞位移xos可知静阀滞后开启时间tos,因此阀球运动初始条件为:
(10)
阀球上升到最大高度时,会与阀罩碰撞而反弹,则阀球运动边界条件为:
(11)
式中:hsm为阀罩限制的最大上升高度,m;CR为弹性恢复系数;vm为最大上升高度时阀球速度,m/s。
由柱塞速度与阀球滞后落座时间tcs可知柱塞位移为xcs。柱塞到达上死点时静阀未关闭,此时泵内压力等于泵吸入口压力,则固定阀滞后关闭时间为:
(12)
式中:ρs为静阀阀球密度,kg/m3。
同理分析动阀规律,可得动阀滞后开启时间tod内的柱塞位移xod,以及滞后落座时间tcd内的柱塞位移xcd。则抽油泵阀隙漏失量为:
(13)
式中:Q2为阀隙漏失量,m3/s;S为泵筒截面积,m2;Sp为柱塞截面积,m2;t为滞后启闭总时间,s。
3 泵效与阀球开启情况
以江苏油田某井为例,各项参数为:游梁式抽油机型号CYJT8-3-26HY,井液密度900 kg/m3,油井深度2 000 m;泵径38 mm,冲程3 m,冲次3 min-1,防冲距0.5 m,泵吸入口压力3 MPa,泵排出口压力15 MPa,阀座型号V11-150,阀球密度7 750 kg/m3,阀球直径23.83 mm。
3.1 悬点运动规律分析
利用三维建模软件建立抽油机模型,运动仿真时曲柄加载2种速率,可得2种驱动方式下抽油机悬点运动规律,如图3所示。
3.2 泵效分析
抽油泵泵效的影响因素主要归结为4大类[13-17]:充满程度η1、液体收缩η2、冲程损失η3及漏失程度η4,则泵效η计算公式为:
η=η1η2η3η4
(14)
漏失程度η4计算方法如式(15)所示,其余影响因素可参考文献[16]计算。
(15)
式中:QT为理论排量,m3/d;ΔQ为漏失排量,m3/d。
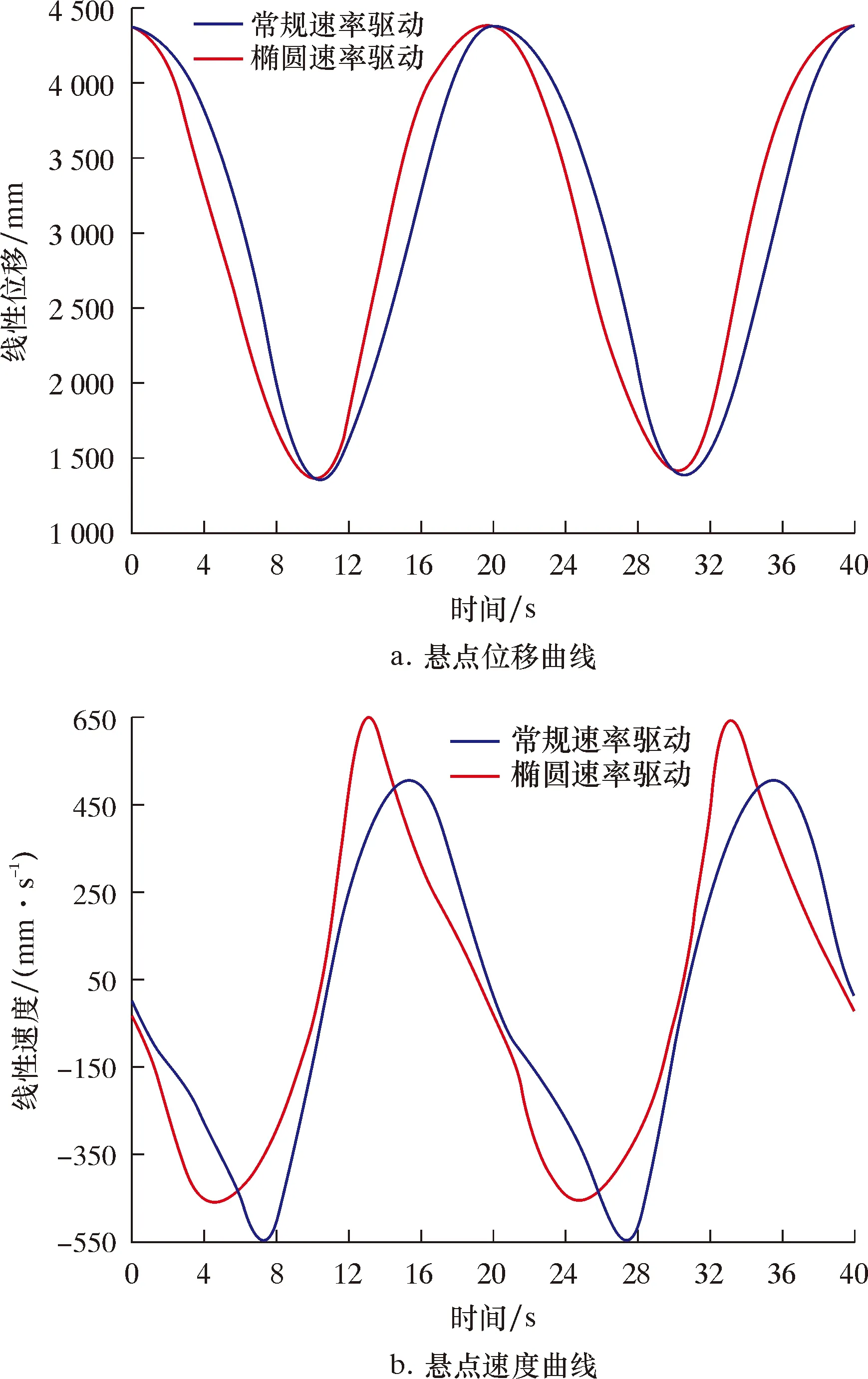
图3 两种驱动方式下悬点运动规律Fig.3 Suspension point motion under 2 driving modes
为便于对接测试试验且椭圆速率主要影响漏失,可将其余影响因素取值为1。根据工作参数,利用上述计算方法可得椭圆速率驱动泵效为94.68%,常规速率驱动泵效为91.79%。由此可知,椭圆速率驱动的泵效比常规速率驱动的泵效提高了2.89%。
3.3 阀球开启情况分析
以静阀静止位置为原点,以上行程方向为正方向建立一维坐标轴。由于动阀的常微分方程组与静阀相似,可假设动阀的结构和尺寸与静阀一致。根据工作参数,利用式(2)~式(11)的阀球运动微分方程组可计算出阀球运动规律。从中截取阀球部分位置情况,结果如表1所示。
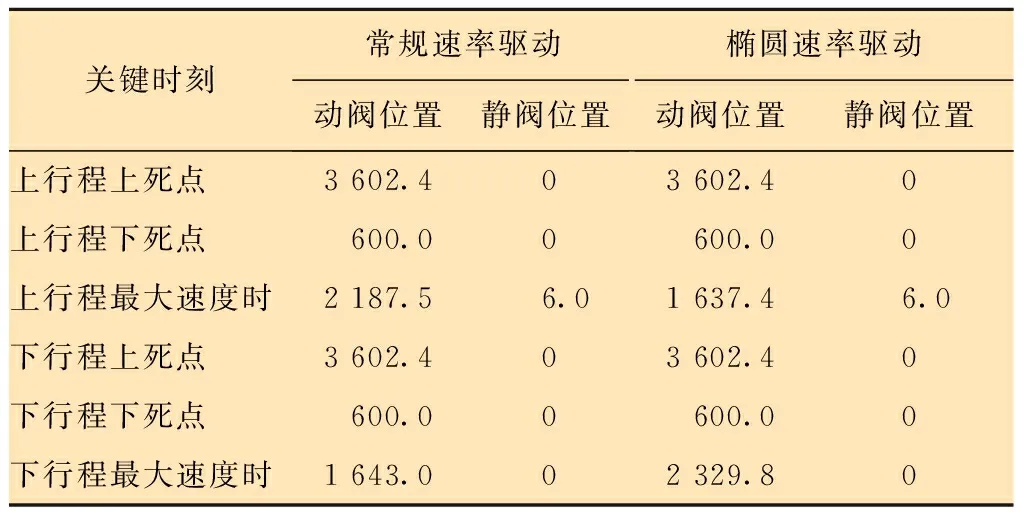
表1 2种驱动方式下关键点时阀球位置 mm
4 基于ANSYS的抽油泵流场分析
结合上述分析,利用ANSYS研究流体进泵过程中泵阀内部流场。根据图2所示抽油泵结构,做以下基本假设:①抽油泵简化为二维图形,且只保留流动区域;②采用静态分析法观察关键时刻流场情况,阀球简化为定边界;③泵阀孔口简化为速度入口,不考虑阀罩;④忽略漏失影响[18-20]。抽油泵流域简化模型如图4所示。

图4 流域简化模型Fig.4 The fluid domain simplified model
图4中圆形代表阀球(上行程时为静阀阀球,下行程时为动阀阀球),且圆形位置与所分析时刻阀球位置相同;模型最下端为速度入口边界,最上端为自由流出边界,其余均为壁面条件;模拟流体采用单相原油,其密度为900 kg/m3、黏性系数为0.17;流体流动情况为湍流,流场温度恒定。
4.1 阀球不同开启状态时的流场分析
利用ANSYS分析阀球不同开启状态时2种驱动方式下的流场,得到阀球开启过程中最大流速的变化曲线,如图5所示。

图5 阀球开启过程中最大流速的变化曲线Fig.5 Maximum flow rate variation during valve ball opening
从图5可知:上行程中以静阀开启量2.3 mm为界,开启量低时椭圆速率驱动的最大流速比常规速率驱动更低,开启量高时更高;下行程时则以动阀开启量4.4 mm为界。结合柱塞速度可知,上、下冲程初始时椭圆速率驱动比常规速率驱动更加平稳,流体进泵速度也能更好地跟随柱塞速度;随着阀球开启量增大,椭圆速率驱动下最大流速逐渐超过常规速率驱动。
4.2 阀球关键时刻的流场分析
结合3.3节的阀球开启情况,以柱塞最大速度时刻为特征,模拟分析得到阀球的流速云图,如图6所示。由图6可以看出,流速在阀球周边的变化最大,同向行程中椭圆速率驱动的最大流速均大于常规速率驱动。
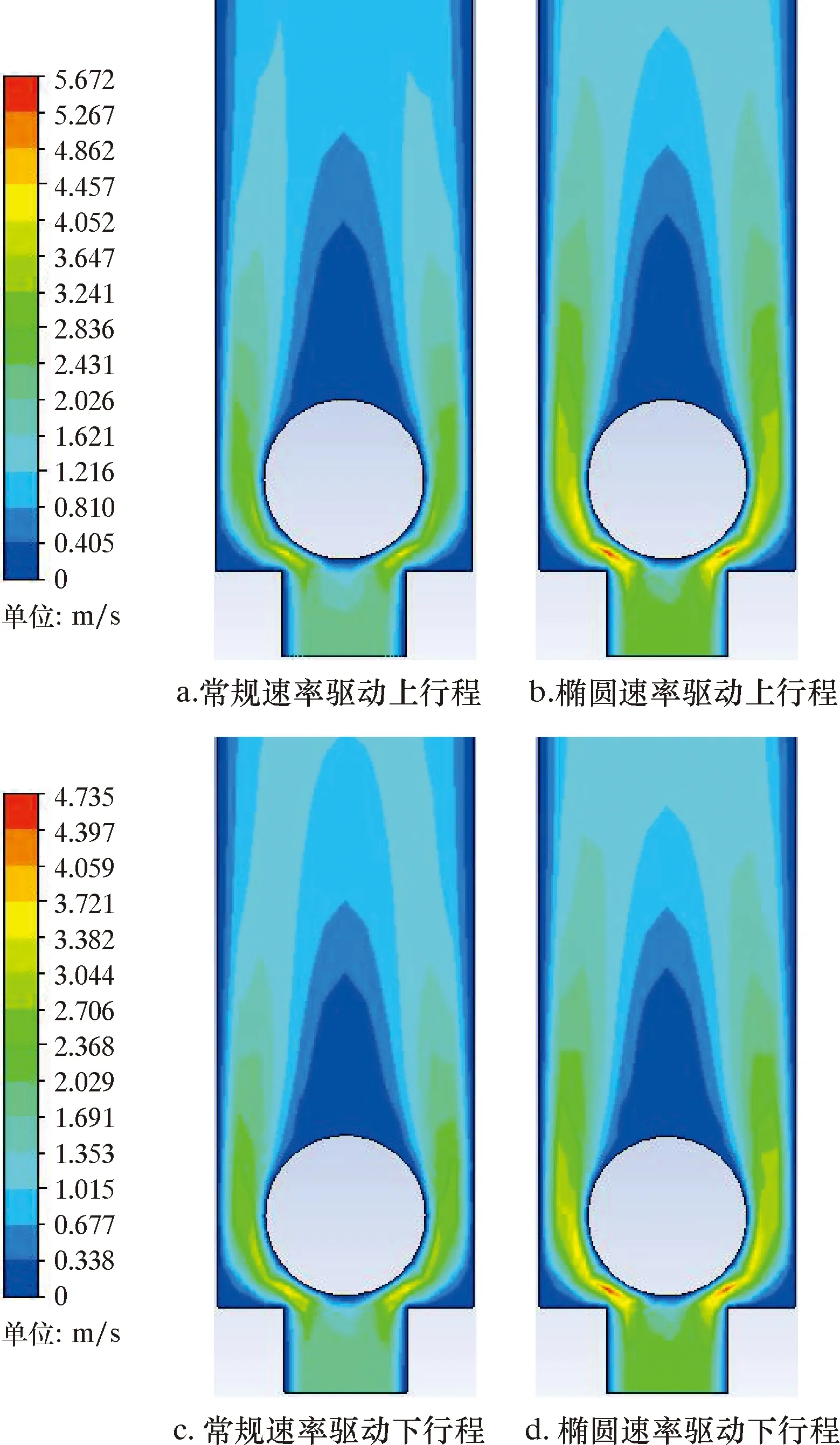
图6 最大速度时刻下阀球的流速云图Fig.6 Flow rate cloud chart of valve ball at the time of maximum speed
4.3 阀球周边流场分析
为深入观测最大速度时阀球周边的流场情况,取阀球周边流速数据进行分析。以圆心为定点,y轴正方向为0°,顺时针方向为正方向建立平面极坐标系(见图7),则上、下行程最大速度时流场流速的变化曲线分别如图8和图9所示。从图8和图9可以看出,在同向行程中,椭圆速率驱动下阀球周边各个位置的流速均快于常规速率驱动。

图7 平面极坐标系Fig.7 Plane polar coordinate system
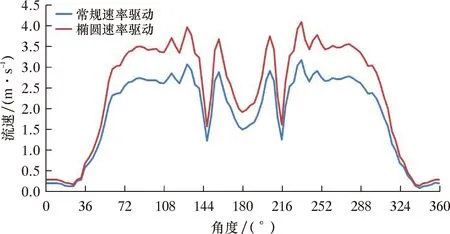
图8 上行程最大速度时流场流速的变化曲线Fig.8 Flow rate variation of flow field at maximum speed in up stroke

图9 下行程最大速度时流场流速的变化曲线Fig.9 Flow rate variation of flow field at maximum speed in down stroke
结合4.1节分析,阀球处于开启状态时,椭圆速率驱动的流速在大部分时间内比常规速率驱动更快,根据漏失计算公式,椭圆速率驱动的漏失量更小,因此椭圆速率驱动的产量更高。
5 测试试验及数据分析
结合选定工况,用1∶4室内模拟试验台架测试分析2种驱动方式的抽油效率。测试试验周期2 min,测试介质为清水和柴油,测试井斜14.0°、32.0°、37.5°和50.0°,测试分析柱形图如图10所示。
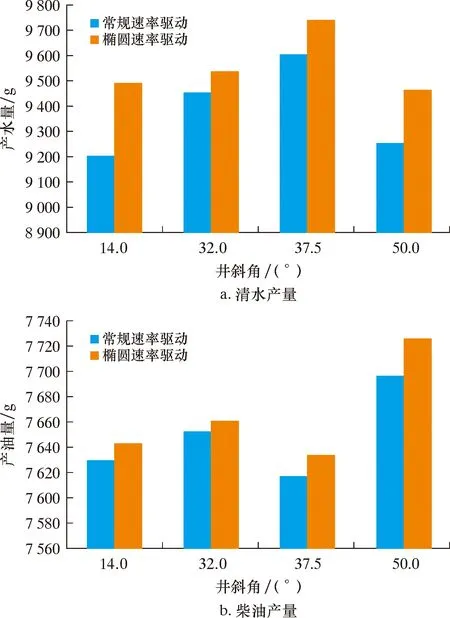
图10 测试分析柱形图Fig.10 Test analysis histogram
由图10可知,椭圆速率驱动的产量比常规速率驱动时均有所提升,最高提升为3.1%。因此,除却试验误差,测试试验规律与理论计算结果一致。
6 结 论
(1)椭圆速率驱动相比常规速率驱动仅改变了柱塞运动规律,主要影响抽油泵的漏失。不考虑其他因素时,通过理论分析得知椭圆速率驱动的漏失量有所减少,泵效比常规速率驱动高2.89%。
(2)对比分析阀球不同开启状态时的流场,上、下冲程初始时椭圆速率驱动更加平稳。通过理论计算可知阀球开启的具体位置,经分析关键时刻的流场可知,阀球完全开启后椭圆速率驱动的漏失量更小,因此椭圆速率驱动方式下的产量更高。
(3)台架试验结果表明,椭圆速率驱动的产量比常规速率驱动时有所提升,最高提升为3.1%,这与理论分析结果一致。

