改进A＊算法与动态窗口法的机器人动态路径规划

槐创锋，郭 龙，贾雪艳，张子昊

华东交通大学 机电与车辆工程学院，南昌330013

在移动机器人诸多技术的研究中，路径规划是技术研究中的重要部分之一，是机器人研究领域的热点，目的是在有障碍物的环境中按照某一种评价指标寻找一条从起始点位置到目标点位置的最优无碰撞路径[1-2]。

栅格法环境建模的经典方法，通过利用栅格对环境信息进行表示，栅格的大小决定了环境信息储存量的大小以机器人进行路径规划的时间长短[3-4]。A*算法[5]是路径规划算法中经典的启发式搜索算法。A*算法由Hart等[6]提出，结合Dijkstra算法和最佳优先搜索算法的优点。文献[7]改进A*算法，在启发函数中加入余弦相似性和方向信息，做归一化处理。文献[8]提出改进A*算法的扩展搜索邻域的思路，利用最小二叉堆优化A*算法OPEN列表存储结构提高搜索效率，但无法完成动态避障。文献[9]成功地扩大搜索邻域，通过重新定义中心节点的位置，在每个节点的周围扩大无限可搜索邻域，较为快速实现无碰撞路径规划。文献[10]基于A*算法，设计了优化的启发搜索函数，选取策略是使用关键点，剔除多余路径点以及非必要的转折点。文献[11]通过引入二次A*算法，减少路径轨迹冗余点，缩短路径长度并且采用自适应圆弧优化算法与加权障碍物步长调节了算法，采用预瞄偏差角追踪法捕捉移动目标点，有效提升路径规划效率。文献[12]以时间耗费作为评价指标，假设AGV 通过每个弧或节点的时间成本是固定的，改进A*算法通过搜寻最小时间耗费来选择最优路径。文献[13]A*算法的改进，创新了高层建筑逃生路径规划算法，对节点扩展优化、权值优化方面进行改进。文献[14]修改A*算法的地图信息，扩展了一层障碍物，改进了代价函数F作二次扩展，并且考虑机器人半径。

针对传统路径规划算法无法高效地、安全地完成动态环境下的路径规划，将传统A*算法扩展搜索邻域，去除了扩展邻域同方向的子节点，改进成了7×7 的A*算法。然后基于改进7×7的A*算法和动态窗口法的移动机器人在栅格法环境模型中实时仿真动态路径规划。

1 改进的A＊算法

1.1 传统A＊算法

A*算法是启发式的搜索算法，可以实现全局路径规划。根据定义的估价函数在静态环境模型中搜索理论上的最优路径，则代价函数表示为：

式中，n代表当前节点；f(n)是当前节点n的代价函数；g(n)为移动机器人起始节点到达当前节点n的实际代价值；h(n)是从当前节点n到达目标点的代价估计值，是代价函数中最重要的部分，正确地选择h(n)能够提升A*算法的成功率和准确性。选取欧氏距离作为h(n)的代价函数，函数表示为：

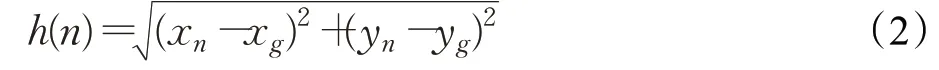
式中，(xn,yn)代表当前路径节点所在栅格中心的坐标，(xg,yg)代表目标点节点所在栅格中心坐标。传统的A*算法搜索从起始点到达目标点的最优路径过程中，规划的全局路径存在多余节点，运动轨迹折线较多，在路径节点处存在转折角度过大以致于不符合移动机器人运动学原理等缺陷，为此提出一种改进的A*算法。

1.2 改进7×7的A＊算法

传统A*算法搜索扩展节点采用3×3 邻域算法，如图1 所示。任意搜索方向之间夹角均为0.25π，节点转折角均为0.25π 的倍数，因此传统A*算法的规划路径不是理论最短，而且规划路径上因为转折点较多、转折角过大不够平滑。

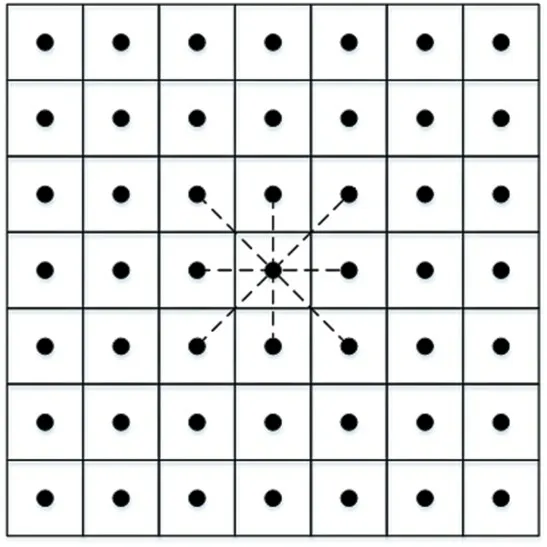
图1 传统3×3的A*算法邻域搜索图

针对传统A*算法3×3 的邻域搜索缺陷，提出扩展A*算法搜索邻域。以图1中7×7正方栅格图为例，当前节点n位于中心节点，其周围第一层（3×3 的邻域）中8个节点是传统A*算法待扩展的节点。改进算法除了采用3×3邻域搜索算法外，还采用当前节点n周围第二层即5×5 的搜索邻域，共计16 个节点纳入算法待扩展节点，算法待搜索邻域节点数即为24个，节点移动方向是16个方向，改进之处在于去除同方向的多余子节点，则改进5×5的A*算法待搜索节点个数减少为16个。这样既扩大了搜索邻域，优化了搜索角度，又提高了算法效率，如图2 所示。当A*算法的扩展搜索邻域到达第三层，如图3所示为7×7的搜索邻域，去除同方向的多余子节点后，待搜索邻域个数为32，可移动方向为32，则将传统A*算法成功改进为7×7的A*算法。

图2 改进5×5的A*算法邻域搜索示意图

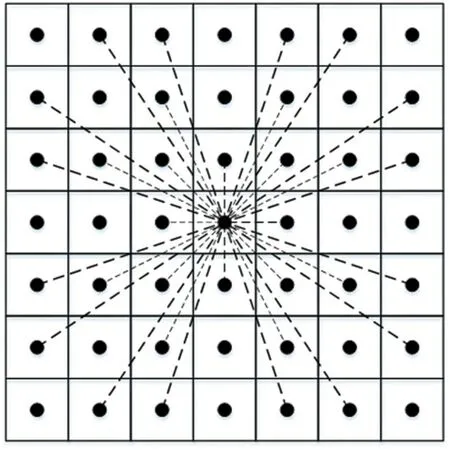
图3 改进7×7的A*算法邻域搜索示意图

2 动态窗口算法

传统DWA 算法进行规划时，缺少全局规划路径的指引，只有目的地位置方向的指引，而中间具体路径是对环境中的障碍物及时避障实时规划的路径[15]。然而，在障碍物较多情况下，移动过程容易陷入局部最优，导致全局路径距离变大。将改进的7×7的A*算法与动态窗口算法进行融合，在局部路径规划时，机器人对临时设置的未知动态障碍物成功规避，安全高效地到达目标点位置，完成了全局路径规划。

动态窗口法，是基于机器人运动学和动力学的一种局部路径规划算法，将路径规划问题转化成为速度矢量空间上的约束优化问题。动态窗口法的目的是：在速度二维空间中采样多组速度（线速度、角速度），在一定时间间隔内，同时模拟移动机器人在这些速度下的轨迹。获取多组可行轨迹后，根据设计的评价函数，选取最优轨迹所对应的速度（线速度、角速度），驱动机器人完成局部路径规划。

2.1 机器人运动学模型

动态窗口算法针对窗口区域内移动机器人的速度进行空间采样，并且模拟出移动机器人的运动轨迹。机器人的运动状态由机器人的线速度和角速度来反馈，(vt,wt)表示轨迹，通过评价函数在所有可行轨迹里选取最佳轨迹，在时间间隔Δt内，假设机器人作匀速直线运动，运动学模型为：

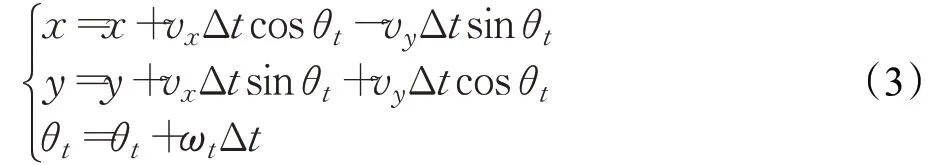
2.2 机器人速度采样

在速度空间中存在无穷多组(v,ω)，要依据机器人的实际情况对采样速度的范围进行约束。

（1）机器人的速度约束为：

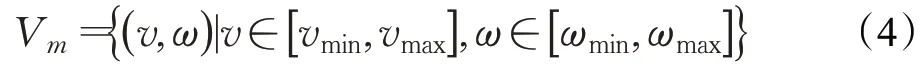
（2）机器人电机加减速约束。动态窗口移动时间间隔内，机器人加速度所带来的最大、最小速度为：

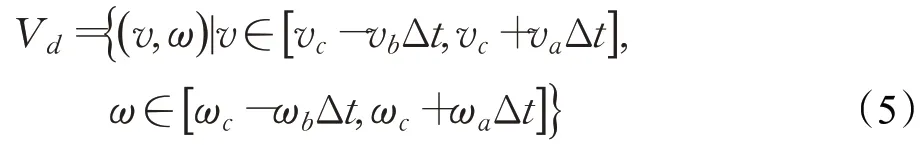
式中，vc、wc代表当前速度；va、wa代表机器人最大加速度；vb、wb代表机器人最大减速度。

机器人制动距离约束。在局部路径规划时为了确保机器人安全，在最大减速度条件要求下，机器人在撞击障碍物之前速度减为0，则：

式中，dist(v,w)是(v,w)对应轨迹距离障碍物的最近距离。

2.3 机器人评价函数

速度空间存在若干组的采样速度是可行的，于是设计评价函数以便选取机器人最优轨迹。评价函数设计准则为局部路径规划，机器人应尽量避开障碍物，用最短时间到达目标点位置。设计的评价函数为：

式中，方位角评价函数head(v,w)，代表了当前速度下模拟轨迹终点位置方向与目标位置之间的方位角偏差；轨迹与静态障碍物的最近距离为dist(v,w),vel(v,w)为当前模拟速度大小的评价函数；σ为平滑系数；α、β、γ为3项的加权系数。

3 融合算法

传统DWA 算法进行规划时，缺少全局规划路径的指引，只有目的地位置方向的指引，故采用改进7×7 A*算法进行全局路径规划，融合动态窗口法进行动态避障，提升动态规划路径的全局最优性。

为了提升实时避障在路径转弯处的能力，提高路径平滑性，在避障过程中，需要实时预估路径的弯曲程度，遇到急弯时提前减速。为每个子目标点Gi添加一个参数Δθ表示全局路径在该子目标点的弯曲程度，Δθ是Gi分别与前后两个相邻子目标点的夹角。当Δθ接近π时，相邻两个子目标点连线的方向近乎平行，机器人以较高的速度运行，当Δθ接近直角时，路径的弯曲程度较大，机器人应降低速度规划平滑路径准备转弯。当运动轨迹近乎直线时，机器人线速度较大，当路径需要避障转弯时，线速度降低，增加路径平滑度。

为避免动态窗口算法陷入局部最优，设计了一种全局最优路径的动态窗口评价函数：

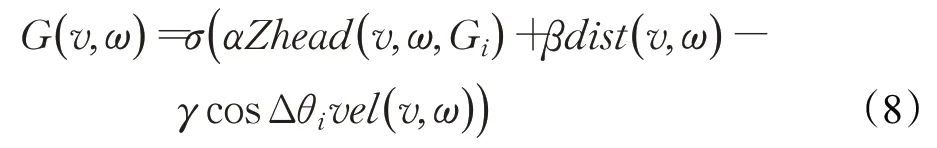
式中，Zhead(v,w,Gi)为模拟轨迹终点方向与子目标点之间的方位角偏差。Δθi是Gi分别与前后两个相邻子目标点的夹角，子目标点Gi是机器人静态规划下的前进方向上距离当前点最近的静态环境下的全局最优路径点。此评价函数使得局部路径规划遵循全局路径规划路径序列点，从而保证全局路径最佳。

3.1 完成全局规划和临时动态避障

为验证所提融合算法在复杂环境中进行动态路径规划的有效性，在所建的栅格图环境模型中，首先标定目标点的位置和机器人起始点的位置，应用算法进行仿真验证，图4栅格地图环境中可以看出机器人避开所有静态障碍物到达目标点位置，完成了静态环境下路径规划。

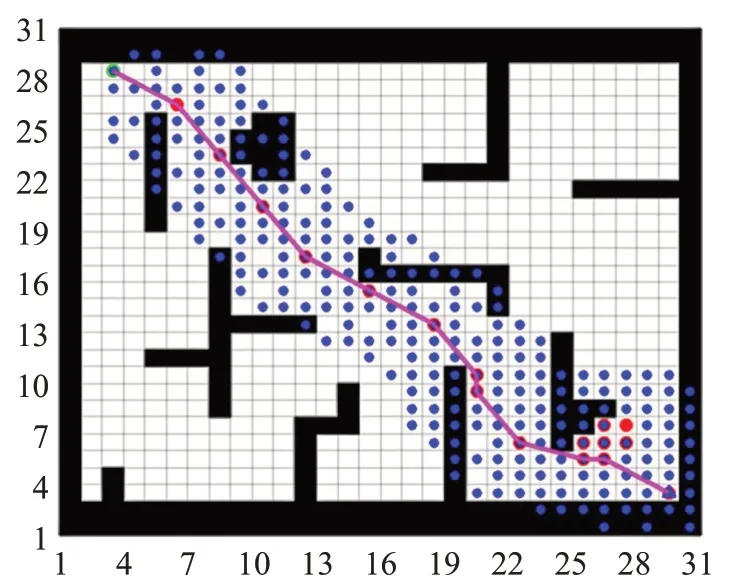
图4 融合算法静态环境路径规划

为了验证动态环境下的路径规划，在机器人规划好的路径上临时设置动态障碍，红色的方块即为设置的动态障碍物。图5中的运动轨迹是机器人规划好的路径，在路径上放置障碍物，绿色的箭头为机器人的运动方向。图6 为移动机器人初始到结束动态路径规划的过程图，显示了移动机器人成功地避开动态障碍物到达目标点位置。从图5、6 可以看出，改进的融合算法，可以实现局部路径规划，躲避动态障碍物，还能得到平滑而且安全的规划路径。

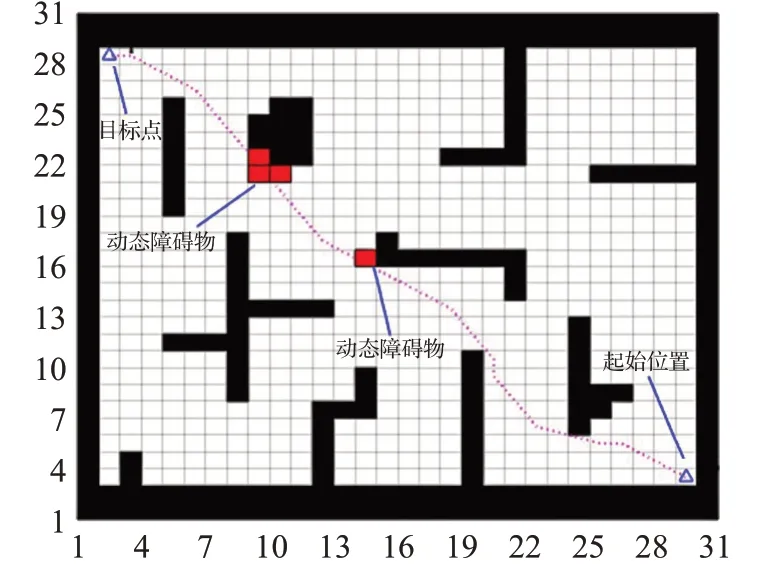
图5 临时设置动态障碍物

3.2 输出运动参数

所改进的融合算法可实时输出机器人的控制参数，有利于机器人的自动反馈控制，机器人线速度的变化、机器人姿态（弧度）的变化、机器人角速度的变化结果如图7 所示。图7 反映了机器人动态路径规划时，控制参数的变化，当机器人局部路径躲避障碍物时，线速度减小，弧度也减小。

3.3 验证算法高效性和适用性，对比其他算法

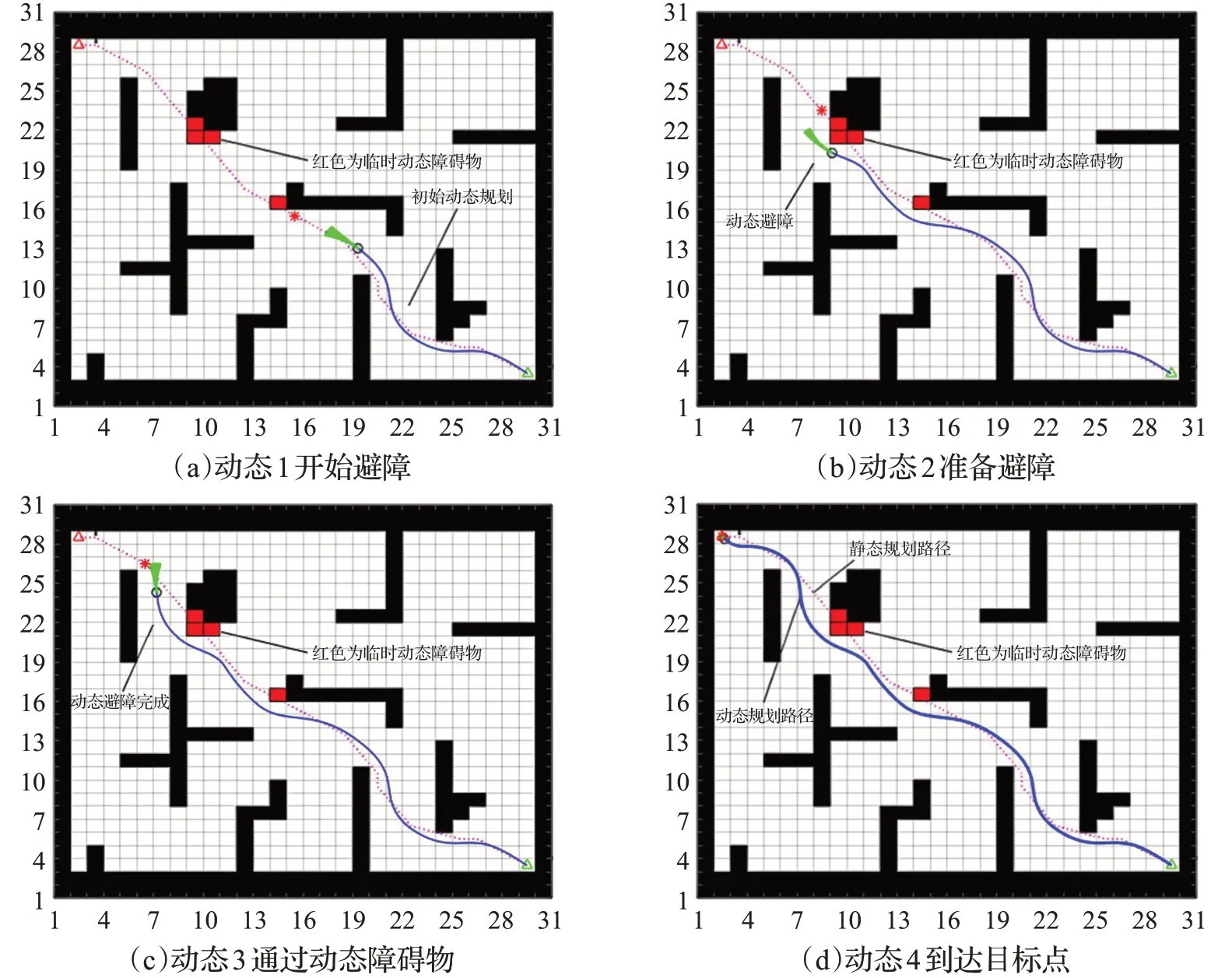
图6 动态避障路径规划图

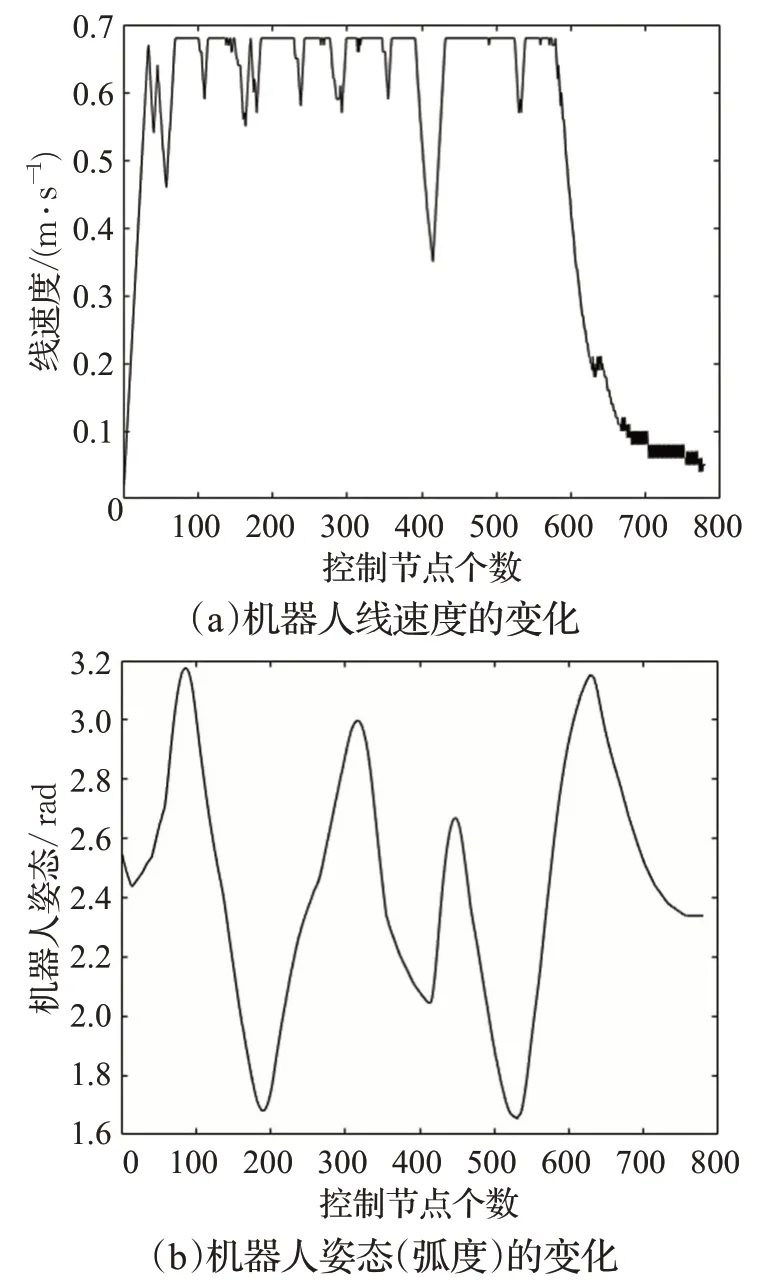
图7 机器人的控制参数变化图

为了验证基于改进7×7的A*算法与动态窗口法的融合算法的高效性，与标准A*算法、改进7×7的A*算法在相同的仿真环境中作出对比，仿真实验结果如图8所示。每组重复仿真10 次，取平均值记录路径规划的时间和路径长度，各种算法的性能指标如表1所示。

图8 三种算法全局路径规划仿真图

表1 三种算法性能指标的对比

由图8、表1可知，三种算法都能够在静态环境下规划出从起始点到目标点的路径。传统A*算法路径转折角多，转折角度大，改进的7×7的A*算法平滑性最好，路径最短，用时最少。

将3×3的搜索邻域扩展为7×7后，同时去除扩展邻域同方向的多余子节点，实质上搜索方向由8个增加到32个，优化了搜索角度；从表中可以看出改进7×7的A*算法距离为40.563 4 mm，时间为0.038 546 s。传统A*算法路径距离为40.870 1 mm，时间为0.060 966 s。改进7×7的A*算法增加了搜索方向，并没有因为增加算法计算量而延长路径规划时间，相反因为优化了搜索角度，取消了节点移动方向仅为0.25π的整数倍的限制，提高了搜索效率，因此减少了路径规划时间；并且改进7×7的A*算法优化了全局路径，减少了路径长度，增加了路径平滑性，可以表明改进7×7 的A*算法比传统A*算法更具有适用性。

相比传统A*算法和改进7×7 的A*算法，基于改进7×7的A*算法与动态窗口算法的融合算法，规划路径更短为38.612 2 mm，平滑性更好，路径规划更好。

4 结论

将传统A*算法，扩展其搜索邻域同时去除了同方向的多余子节点，改进为一种7×7的A*算法，有效地消除了传统路径转折角多、转折角度大的缺陷。为提升在动态复杂环境下移动机器人路径规划效率，提出一种基于改进7×7的A*算法与动态窗口法的融合算法，设计了一种全局最优路径的动态窗口评价函数，采用动态窗口算法实现路径的局部规划，成功规避了挡住已规划好路径上的动态障碍物，机器人规划出了从起始点到目标点的最优路径。通过与多种算法仿真分析比较，结果表明了提出的融合算法具有可行性和高效性。