基于钻柱动力学的平磨优化设计及现场试验

刘宝振， 张中国， 石 义， 邹 明， 李方园， 王学迎， 倪红坚

(1中石油西部钻探公司井下作业分公司 2中国石油大学石油工程学院·华东)

0 引言

在原有井眼基础上，小井眼加深井作业可以有效加快勘探开发进度，节约资金[1- 6]。新疆油田公司每年需进行15～25口井的小井眼加深井作业。加深井施工分为原井眼的修复阶段和加深钻井阶段，当前的技术难点主要集中在原井眼的修复阶段，表现在磨浮箍浮鞋时间长、效率低。

人工井底难磨的原因有两个，一是浮箍浮鞋包含铁和铝合金部件；二是部分浮箍浮鞋中心含有金属质圆轴。在研磨时由于平底磨鞋中心的线速度几乎为零，因此中心部分的金属圆轴很难磨掉，有时需要超过10 d时间才能磨穿一个人工井底，严重制约了钻井提速。

为解决上述问题，笔者曾设计了中心大水眼的新型平底磨鞋，这种新磨鞋通过避开中心部位来提高研磨速度，但每磨进一段距离，中心的孔眼就会被金属圆轴堵死，造成泵压急剧升高。

针对上述问题，笔者从钻柱动力学角度出发，通过重新设计BHA组合和磨鞋尺寸，在旋转离心力的作用下，使磨鞋中心适当偏离井底中心，从而提高井底中心处的研磨速度。现场试验证明了新的设计可以大幅地提高研磨速度，缩短钻井周期。

1 钻柱动力学模型及井底线速度分布

1.1 钻柱动力学模型

如前所述，解决上述平磨问题的核心思想是改变磨鞋中心在井底的位置，为了分析不同磨鞋尺寸、BHA组合和钻井参数下的磨鞋轨迹，需要建立钻柱动力学模型。

参考文献[7- 16]，将磨鞋、钻铤和钻柱看作是空间圆柱形梁单元，该梁单元具有两个节点、12个自由度，每个节点有3个平动和3个转动自由度，如图1所示。

图1中包含3套坐标系，分别为整体坐标系OXYZ、节点坐标系ξηζ和基于每个单元的局部坐标系，三个坐标系的方向一致，可以简化为一个整体坐标系。

钻柱系统的动力学平衡方程可表示为:

(1)

图1 钻柱系统梁单元模型

刚度矩阵K可以表示为:

K=KL+KNL

(2)

式中:KL和KNL—分别为线性和非线性刚度矩阵。

阻尼矩阵C可以用瑞利阻尼代替，表示为:

C=αM+βKL

(3)

式中:α和β—阻尼系数，对于常规钻井液钻井[10]，α∈[0.03,0.05]，β∈[0.1,0.3]。

文献[9]给出了上述各矩阵M、KL和KNL的具体表达式，以及重力、离心力的单元等效节点力表达式，这里不再赘述。

对平磨作业而言，钻柱在套管内运动，因此在处理钻柱单元节点与井壁的碰撞时，可以忽略碰撞过程，认为碰撞是在一个时间步内完成的，使用速度恢复系数法[4]描述碰撞过程。

碰撞前后速度关系为:

(4)

式中:cr—速度恢复系数;v1和v2—表示碰撞前后的速度大小。

碰撞过程中钻柱与井壁之间的径向接触力fr为:

fr=-[ur-(db-do)/2]kh-vrcf

(5)

钻柱旋转，还将产生摩擦力ft和摩擦力矩T:

ft=μfr

T=ftdo/2

(6)

式(5)、式(6)中：ur—钻柱节点的径向位移;db和do—分别为钻头直径和钻柱外径;vr—钻柱节点的径向速度;kh和cf—分别为井壁的刚度系数和碰撞能量损失的等效阻尼系数；μ—钻柱与井壁之间的摩擦系数。

采用Newmark-β法求解上述钻柱动力学方程，编程语言采用Matlab，为充分发挥Matlab的矩阵运算优势，采用整体刚度矩阵法求解。

1.2 井底线速度分布

如图2所示，求得钻头在井底的运动轨迹后，可以计算井底任一点处的平磨线速度，若该点在钻头半径覆盖范围外，则线速度为零，若在钻头半径覆盖范围内，则可以用转速和该点到钻头中心的距离计算平磨线速度，如式(7)所示。

(7)

式中:vl—该点的线速度，用极坐标下的角度θ和半径r确定该点的位置;dt—该点到钻头中心的距离。

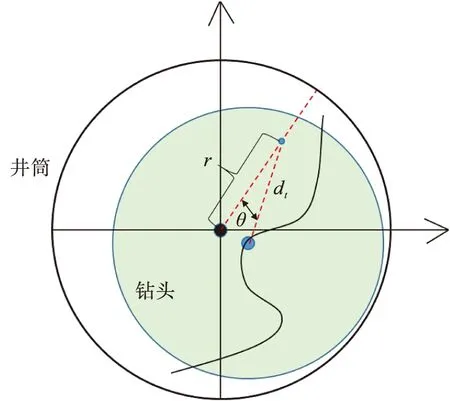
图2 井底线速度计算示意图

通过计算一段时间内的钻头线速度在井底平面的分布，可以判断磨鞋对井底各处的磨损速度，从而选择合适的磨鞋尺寸、BHA组合和钻进参数。

2 数值模拟结果及分析

2.1 原设计参数下井底线速度分布

选择新疆油田典型的小井眼加深井作业开展数值模拟研究，井型均为直井，最初的钻具组合如表1所示，钻压20～40 kN，转速70 r/min，套管内径159.4 mm。

表1 初始钻具组合

图3给出了在原始钻具组合和钻井参数设计下井底的平磨线速度沿某条半径方向的分布图。可以看出最大平磨线速度的位置靠近井底平面的外侧，但紧邻套管处线速度为零，这一点与现场实际情况一致，即钻头磨过后仍有附着物附着在套管内壁上。整体而言，井底中心处的线速度要小于外侧，最大线速度是中心处线速度的22.5倍。因此，提高平磨机械速度的关键是提高井底中心处的线速度。

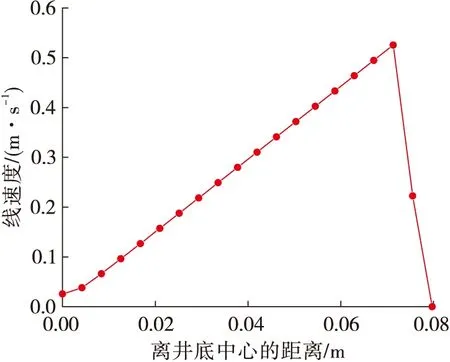
图3 原设计下井底平磨线速度径向分布图

2.2 钻铤尺寸的影响

在平磨作业中，钻具组合往往是参考钻井的相关标准和规范设计的。通过设计一段或多段尺寸较大的钻铤来施加钻压，保证钻铤承受轴向压力，而钻杆不受压。这种设计可以保证下部钻杆不屈曲，打出的井眼是直的[8]。但是上述设计标准并不适用于平磨作业，平磨作业是在套管内进行的，加上平底磨鞋的特点，不会产生井斜的问题。

图4给出了两个钻头尺寸下，钻铤偏心率为2.25%时的井底线速度沿径向的分布。钻头直径为152 mm时，两种规格钻铤对应的井底线速度分布几乎是一样的，此时钻铤尺寸的影响可以忽略。当钻头尺寸为145 mm时，三种规格钻铤对应的井底线速度分布曲线之间的差别扩大，尤其是在井底平面外缘处，但是最关键的井底中心线速度并没有明显变化。

综合以上分析，钻铤尺寸的影响可以忽略不计，应该选用小尺寸钻铤，或者在井深较浅和钻压要求较低时不用钻铤，结合当前平磨施工的实际情况，可使用Ø88.9 mm钻铤替换Ø120.7 mm钻铤或不使用钻铤。

2.3 磨鞋尺寸的影响

磨鞋尺寸对磨鞋中心在井底的位置有重要影响，例如满眼磨鞋的中心应该是与井底中心重合的，这种情况不利于提高平磨速度，减小磨鞋尺寸有助于加快井底中心部位的研磨，但磨鞋过小也会导致研磨不均匀，需要二次修复井底，为了确定最佳的磨鞋尺寸，改变磨鞋直径进行数值模拟。

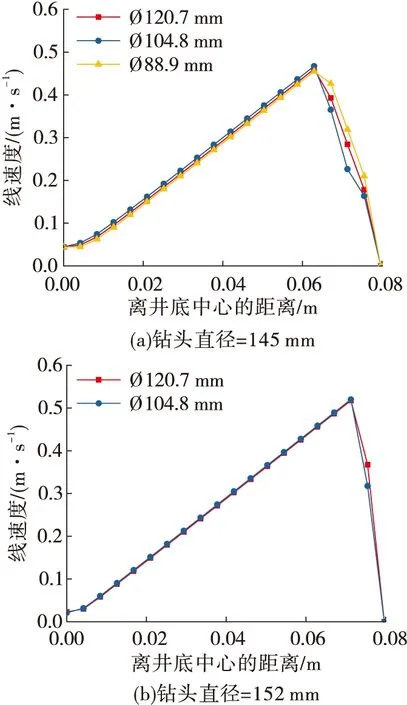
图4 不同钻铤尺寸下井底线速度径向分布

图5给出了不同磨鞋尺寸下的井底平磨线速度分布，从中可以看出三个明显的规律。首先随着磨鞋直径缩小相应的峰值线速度减小，鉴于线速度是转速和半径的乘积，这一规律不难理解。其次，随着磨鞋尺寸减小峰值线速度对应的位置逐渐向井底中心处移动。最后，随着磨鞋尺寸减小井底中心处的线速度逐渐增加。

图5 不同磨鞋尺寸下井底线速度径向分布

因此，缩小磨鞋尺寸将极大地提高井底中心处的线速度和最终的平磨机械钻速。但是磨鞋尺寸也不能太小，例如图5中的Ø105 mm磨鞋所对应的曲线，显著地降低了整体的线速度。

经分析可知磨鞋尺寸对井底平磨线速度的分布有很大影响，考虑到数值模拟参数选取存在的偏差，初步确定合理的磨鞋直径范围在105～125 mm。

2.4 转速的影响

图6给出了不同转速下的井底线速度分布，可以看出不同转速下最大线速度对应的位置是不同的。70 r/min、90 r/min和110 r/min对应的最大线速度位置基本一致，但是50 r/min对应的转速要更加靠近井底外缘，且在0.02 m处有一个速度极小值。显然50 r/min的地面转速将不利于提高平磨线速度。

图6 不同转速下井底线速度径向分布

图7给出了50 r/min和70 r/min两种转速下的磨鞋中心在井底的轨迹分布。从该图中可以看出转速为70 r/min时磨鞋中心经过的区域面积更大，此时磨鞋对井底的磨损更加均匀，也意味着后期修复井壁需要的时间缩短。

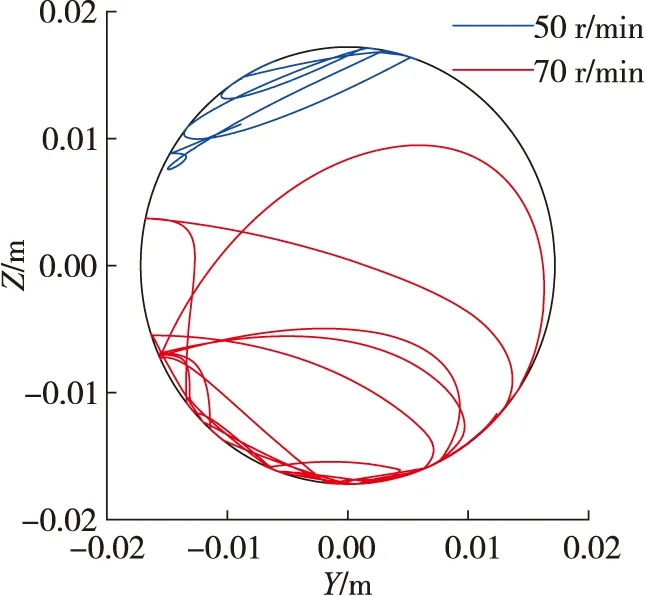
图7 不同转速下磨鞋轨迹在井底的分布

3 现场试验及结果分析

根据上述数值模拟结果，重新设计了BHA和磨鞋尺寸，定制了3个小尺寸磨鞋，开展了3口井的现场试验，试验数据和结果如表2所示，钻压范围2～4 t，转速70～80 r/min，排量60 L/s，泵压8 MPa，钻杆外径为88.9 mm，内径为70.2 mm。试验1#代表原设计下的结果，机械钻速取5个平底磨鞋的平均值。图8给出了不同试验井的平底磨鞋机械钻速。

表2 现场试验设计和机械钻速数据

图8 不同试验井的平磨机械钻速

从图8可以看出，改进的设计大幅地提高了研磨速度，验证了数值模拟结果的正确性。试验井2#(Ø125 mm磨鞋)对应的机械钻速最大，是原设计下平磨机械钻速的3倍。试验井4#(Ø105 mm磨鞋)的提速效果最差，但仍远高于试验井1#。此外，试验井4#的二次修复时间要明显长于试验井2#和3#，说明Ø105 mm平底磨鞋的磨损均匀度差，井底外缘处存在较多附着物，这也与数值模拟结果相吻合。

4 结论

(1)限制平磨机械钻速主要是井底中心处的金属质圆轴，提高中心处的研磨线速度能够有效提高整个平磨作业的速度。

(2)磨鞋尺寸对磨鞋中心在井底的运动轨迹影响最大，钻铤直径和转速等其他因素影响较小，首先调整的变量应该是磨鞋直径。

(3)大尺寸钻铤对平磨施工的作用较小，且会加重钻机负荷，建议使用小尺寸钻铤或加重钻杆，或者不使用钻铤。