基于某高层框架与剪力墙隔震结构的高宽比限值研究

孙 蓉， 齐毅男

（震安科技股份有限公司， 昆明 650217）

0 引言

隔震技术近些年在我国飞速发展， 北京新机场航站楼、 北京城市副中心等重要项目均采用隔震技术。 截至2017 年底， 全国累计建成的隔震项目多达4295 个（项目个数）[1]。 目前该技术已更多地在高层建筑、 复杂结构中得到应有[2]。 在日本， 建于1999 年超高层隔震建筑仙台森大厦经过2003年仙台地震的考验， 证明高层隔震仍能获得很好的减震效果。 在我国， 河北三河市大厂高层住宅，以及90.35 m 高的云南玉溪公共租赁房项目均为高层隔震项目。

现有建筑抗震规范只规定结构高宽比限值不宜大于4[3]， 没有对不同类型隔震结构的高宽比进行专门限制。 针对该问题， 以剪切型的框架结构和弯曲型的剪力墙结构为例， 研究不同结构类型对基础隔震结构高宽比限值的影响规律。

1 模型概况

根据规范要求， 隔震后结构的高宽比不宜大于4。 本研究中设计了典型16 层框架与剪力墙结构， 其平面尺寸均为22.5×11.5 m， 主体高度45.6 m， 高宽比均为4。 建筑类别为丙类， 场地类别II类， 抗震设防烈度为 7（0.15g）度。 两建筑地上 1层高 3.6 m， 2～15 层层高为 3 m。 用 PKPM 软件分别完成框架和剪力墙结构的抗震设计， 两结构的梁、 楼板截面及荷载分布相同。 PKPM 模型见图1， 首层结构平面布置如图 2、 3 所示。 结构每层平面布置不变， 梁柱尺寸和混凝土型号随结构高度增加而改变。 框架结构层间位移角1/781； 剪力墙结构层间位移角1/1413 两结构的SATWE 计算结果满足规范要求。

图1 PKPM 模型Fig.1 Frame and shear wall structure models developed by using PKPM

2 隔震设计

2.1 非隔震模型对比

用ETABS 9.7.4 有限元软件建立隔震分析模型， 梁柱采用杆单元， 剪力墙采用壳单元、 楼板采用膜单元。 对框架结构和剪力墙结构的ETABS模型和PKPM 模型的质量和周期进行对比， 框架结构ETABS 模型质量为5716.0 t， PKPM 模型质量为 5644.3 t； 剪力墙结构 ETABS 模型质量为5485.0 t， PKPM 模型质量为 5492.6 t， 周期对比结果如表1 所示， 两种软件所建模型的质量和周期误差均在允许范围内。

图2 框架上部结构平面布置图Fig.2 Layout plan of frame superstructure

图3 剪力墙上部结构平面布置图Fig.3 Floor layout of shear wall structure

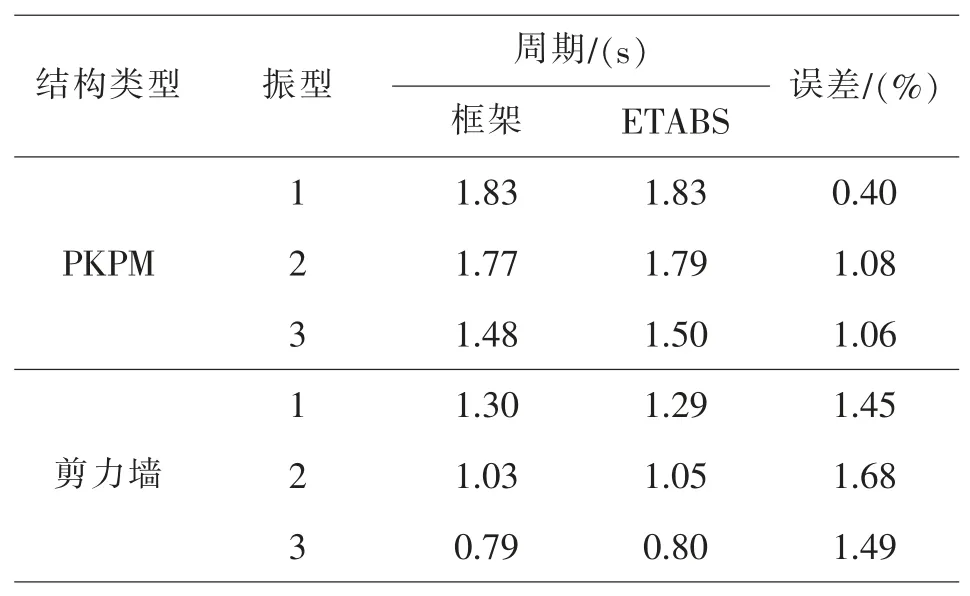
表1 ETABS 模型与PKPM 周期对比Table 1 Period comparison between ETABS model and PKPM model

2.2 支座布置与选取

根据隔震规范规定， 丙类建筑的隔震支座长期面压限值为15MPa， 结合PKPM 模型柱底反力选取隔震支座。 支座型号如表2 所示。 布置隔震支座时， 将铅芯支座布置在隔震层外围， 橡胶支座布置在隔震层内侧， 在保证隔震层质心和刚心重合的前提下， 尽量使两结构相同编号的隔震支座型号相同， 支座编号如图4 所示。

框架和剪力墙两种结构的支座布置如图5、 6所示。 X 向质心和刚心完全重合， Y 向质心和刚心偏差不到1%。 隔震前后结构的动力特性如表3 所示， 两种隔震结构的周期平均延长一倍左右， 隔震前， 结构前三阶振型累计质量参与系数均不到74%； 隔震后框架结构前三阶振型累计质量参与系数可达到97.9%， 剪力墙可达到99.4%， 隔震效果明显， 上部结构基本保持平动。

2.3 地震波的输入

分析所用地震波为四条天然波和三条人工波，天然 波 为： Hachinohe、 Northridge、 Loma Prieta、Turkey； 由于结构规则， 所以地震动输入方式为X向和Y 向单向水平输入， 设防烈度下加速度峰值为 150 gal、 罕遇地震下加速度峰值为 310 gal。 所选地震波低频部分较多， 反应谱长周期段衰减缓慢， 可有效激发结构高阶振型， 有助于对比不同类型基础隔震结构的动力特性， 支座面压受结构高宽比的影响也较为明显。

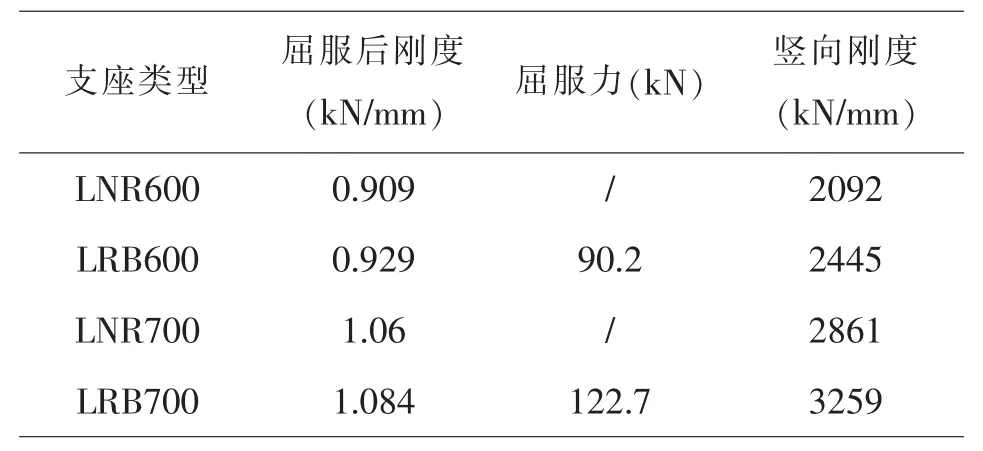
表2 隔震支座参数表Table 2 The mechanical parameters of isolation bearings

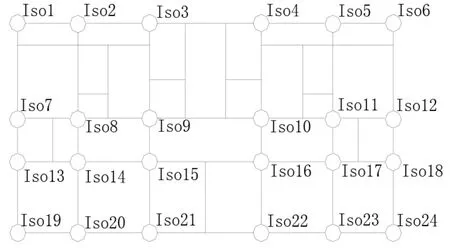
图4 隔震支座编号Fig.4 The serial number of isolation bearings

图5 框架结构隔震支座平面布置图Fig.5 Arrangement of isolation bearings of frame structure

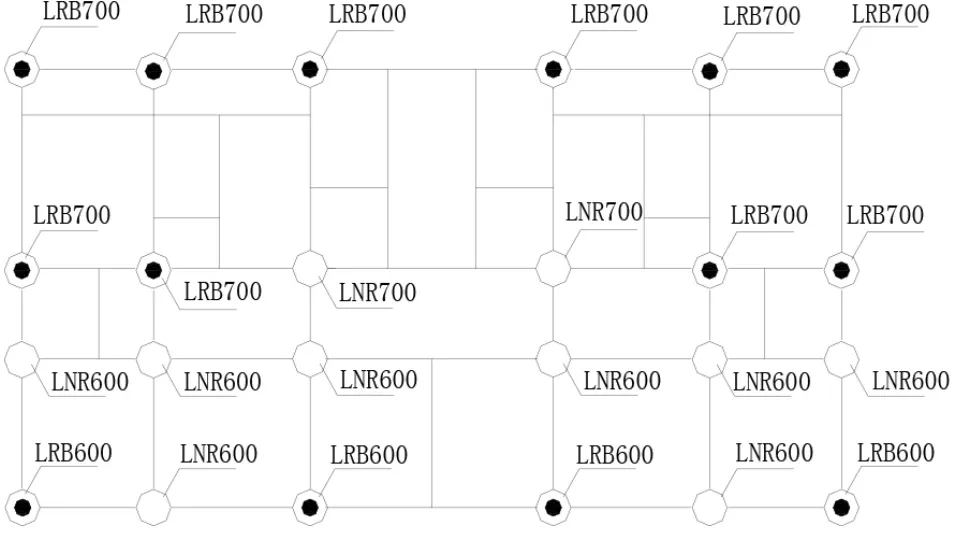
图6 剪力墙结构隔震支座平面布置图Fig.6 Arrangement of isolation bearings of shear wall structure

3 框架与剪力墙隔震结构对比分析

3.1 隔震前后上部结构响应对比

图7 给出了设防地震下框架与剪力墙结构隔震与非隔震的层间内力平均值对比， 由对比结果可知， 隔 震效果明显， 说明基础隔震技术能够有效减小上部结构的地震响应。

图8 为罕遇地震作用下采用基础隔震的框架结构与抗震结构的位移对比， 对比可知非隔震情况下， 框架结构为剪切变形； 隔震后上部结构仍为剪切变形， 但层间位移明显减小。

图9 为罕遇地震作用下剪力墙结构隔震与非隔震情况下的位移对比， 对比可知非隔震情况下，X 向呈弯剪变形； Y 向基呈弯曲变形； 隔震后上部结构仍保持原有变形特征， 但层间位移角明显减小。

表3 隔震与非隔震结构动力特性对比Table 3 Comparison of dynamic characteristics between base-isolated and non-isolated structure

图7 结构隔震前后剪力、弯矩对比Fig.7 Comparison of shear and bending moment before and after structural isolation

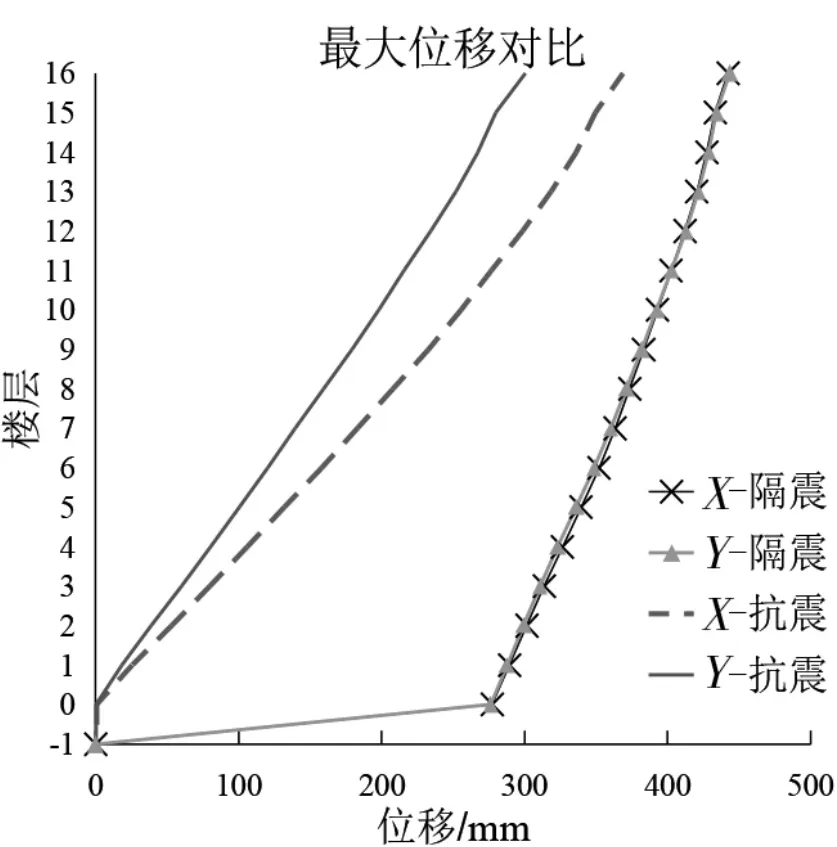
图8 框架结构隔震前后位移比Fig.8 Comparison of displacement of frame structure before and after seismic isolation

3.2 隔震后两种结构响应对比

为了更好地表征两种结构的隔震效果， 本文采用了三个指标， 即 “剪力比”、 “弯矩比” 和“位移角比”， 分别定义如下：

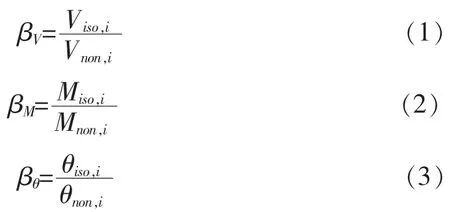
式中： i 为结构楼层号。 Viso，i， Miso，i， θiso，i分别为隔震结构i 层对应的层剪力、 层弯矩及层位移角； Vnon，i， Mnon，i， θnon，i为抗震结构 i 层对应的层剪力、 层弯矩及层位移角。

βV， βM， βθ可直观反映出基础隔震结构每层的减震效果沿结构高度的变化趋势， 对比结果分别如图 10、 11、 12 所示。 图 10 中隔震后结构各层剪力比均在0.4 以下， 根据抗震规范， 上部结构可按降低一度进行设计。 图10 和11 表明， 基础隔震技术可有效减小上部结构的内力响应： 采用隔震技术后， 框架结构层间剪力平均降低75%， 弯矩平均减小70%， 结构中部和底部的层间剪力减小明显， 减震效果沿高度逐渐减小。 剪力墙结构层剪力平均降低80%， 其弯剪变形方向， 剪力比曲线浮动较大， 弯曲变形方向浮动较小， 结构中下部及顶部的减震效果有所下降。 剪力墙结构层间弯矩减小明显， 减小程度沿结构高度逐渐递增，最大可降低90%以上， 结构顶部效果有所减小，但仍可降低70%以上

图9 剪力墙结构隔震前后位移比Fig.9 Comparison of relative displacement of shear wall structure before and after seismic isolation

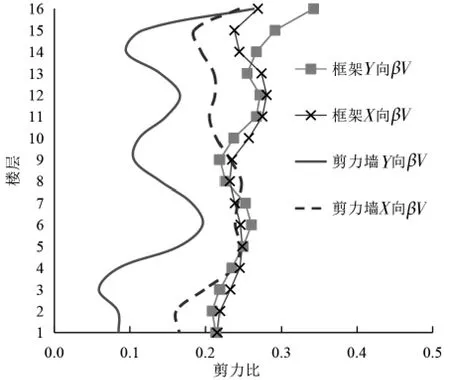
图10 结构剪力比Fig.10 Shear force ratios of frame and shear wall structures

图11 结构弯矩比Fig.11 Moment ratios of frame and shear wall structures

由图12 可知， 在罕遇地震下， 隔震能有效减小上部结构层间位移角， 框架结构X 向层间位移角平均减小55%， Y 向减小45%， 结构的中上部及中下部减震效果下降。 剪力墙结构X 向层间位移角平均减小70%， Y 向减小84%， 且沿结构高度效果递增； 相比与剪切型结构， 弯曲变形结构的βθ曲线波动减小， 说明弯曲型结构隔震后， 层间位移的减小不会沿结构高度而产生明显差异。

图12 结构位移角比Fig.12 Story drift ratios of frame and shear wall structures.

3.3 支座应力对比

时程分析中考虑隔震支座的拉压异性， 采用ETABS 中Isolator1 单元和Gap 单元并联模拟隔震支座， 拉压刚度比取1/7[4-5]。 隔震层的支座编号图4 已给出， 对比两种结构在X 向和Y 向罕遇地震作用下的支座应力， 如图13、 14 所示。 由图可知高宽比为4 的两种隔震结构在罕遇地震下， 19 号和24 号角部支座最先出现拉应力。 对支座面压验算数据进行汇总， 汇总结果如表4 所示。

对比两结构支座应力的汇总结果， 可以看到在罕遇地震作用下， 框架结构X 向和Y 向分别出现了0.9 MPa 和2 MPa 的拉应力， 剪力墙结构支座未出现受拉现象。 此外， 两种结构极小面压和极大面压均值相差不大， 框架结构极小面压方差远大于剪力墙结构。 说明框架的支座面压偏离平均值过大， 各支座所受拉力分布不均， 致使支座出现拉应力。 所以地震作用下， 框架结构更易出现支座受拉现象。 而剪力墙的极大面压方差远大于框架结构， 面压18 MPa 以上的支座占支座总数的30%， 框架结构仅占8%。 说明该剪力墙结构支座压应力分布不均。

表4 支座竖向应力汇总Table 4 Summary of vertical stresses of isolators

图13 X 向地震作用下支座面压Fig.13 Compressive stress of isolation bearing under X direction earthquakes

图14 Y 向地震作用下支座面压Fig.14 Compressive stress of isolation bearing under Y direction earthquakes

4 不同高宽比剪力墙结构的隔震分析

4.1 结构模型

由于框架结构当高宽比到达4 时， 支座拉应力超限， 所以本节仅对大高宽比的剪力墙结构进行分析， 研究该剪力墙结构所能达到的极限高宽比。 以高宽比为4 的剪力墙模型为基础， 采用增加楼层高度的方式增加结构的高宽比。 不同高宽比的结构高度如表5 所示。

表5 不同高宽比结构对应高度Table 5 The height of structures with different aspect ratio

采用 PKPM 软件对高宽比为 5、 6、 7 的三栋剪力墙结构进行抗震设计， 增加结构高度过程中，不改变结构的平面布置和荷载分布， 仅对梁柱截面和混凝土型号进行更改， 用SATWE 进行计算，使结构轴压比、 层位移角及剪重比等指标满足规范要求。

对ETABS 模型的质量和周期进行校核， 高宽比为 5、 6、 7 的 PKPM 模型质量分别为 6792 t、8100 t、 9420 t 与 其 对 应 的 ETABS 模 型 质 量 为6744.6 t、 8026.7 t、 9306.5 t， 误差均在 1%以内。周期对比结果如表6 所示

表6 ETABS 模型与PKPM 周期对比Table 6 Period comparison between ETABS and PKPM models

4.2 隔震设计

按照第2 节的隔震设计步骤， 对三栋剪力墙结构进行基础隔震设计， 选用支座型号时力求符合实际隔震设计原则， 从小直径的支座开始选取，铅芯支座分布于隔震层外围。 支座参数如表7 所示。 随结构高宽比的增加， 为满足隔震层水平刚度， 保证支座水平位移和支座长期面压不超过规范要求。 增加了支座的直径； 同时为了保证隔震层质心和刚心的重合， 调整了个别铅芯支座的位置。

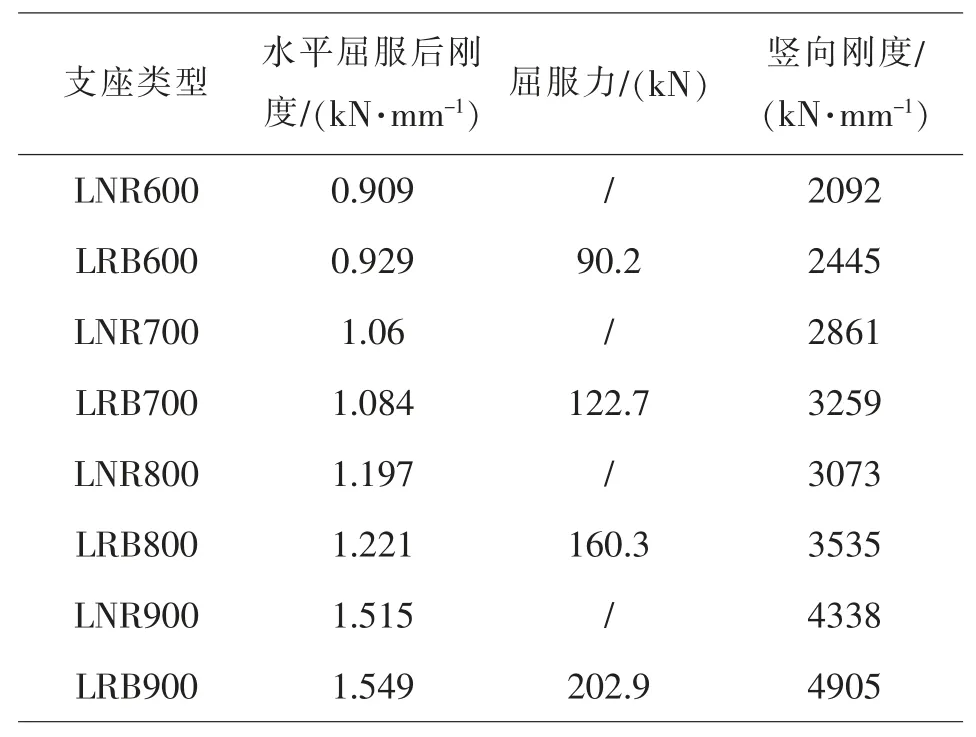
表7 隔震支座参数表Table 7 The mechanical parameters of rubber bearings

4.3 隔震分析

不同高宽比的剪力墙结构， 隔震后前三阶振型X 向和Y 向的累计质量参与系数均达到95%以上； 结构周期延长效果明显。 此处引入 “周期比”概念，

式中： Tnon， Tiso， 分别为隔震前后结构的周期，βT为周期比， 用以衡量不同高宽比的剪力墙结构基础隔震后， 周期的延长效果。 不同高宽比结构的前三阶周期比如图15 所示。 对比不同高宽比结构X 向和Y 向的最大剪力比， 结果如图16 所示。

由图15 可知剪力墙结构随高宽比的增加， 隔震后周期延长的效果减小， 但隔震后前三阶周期仍是隔震前周期的1.5 倍以上。 由图16 可知， 剪力墙隔震结构的减震系数随高宽比的增加而变大，由图中最大剪力比曲线可知， 弯剪变形方向的剪力比曲线波动较大； 弯曲变形方向的剪力比始终保持在0.3 以下， 由此可知： 结构高宽比增加对弯曲型隔震结构的减震系数影响不大， 但会导致弯剪型结构减震系数变大。 不同高宽比的剪力墙结构采用基础隔震后， 减震系数均保持在0.4 以下， 仍能取得良好的隔震效果， 可按降1 度进行抗震设计。

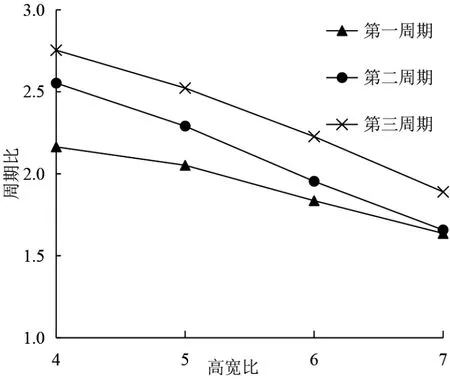
图15 不同高宽比结构周期比Fig.15 Period ratio of structures with different aspect ratio

图16 不同高宽比结构最大剪力比Fig.16 Maximum shear force ratio of structures with different aspect ratio

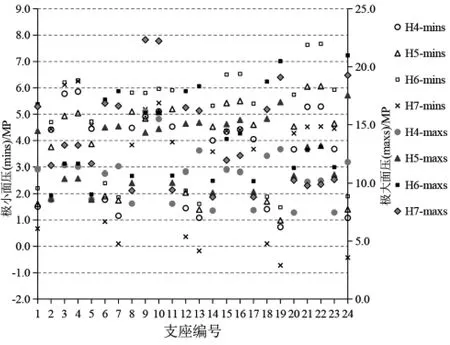
图17 X 向地震作用下不同高宽结构支座面压Fig.17 Compressive stress of isolation bearing with different aspect ratios under X direction earthquakes

4.4 隔震支座应力对比

高宽比分别为 4、 5、 6、 7 的剪力墙隔震结构在罕遇地震作用下的支座面压如下图17、 18 所示。

由图可知地震作用下， 最大面压和最小面压均出现在结构角部的隔震支座。 高宽比为7 的隔震结构， 支座最大面压是27 MPa， 最小面压为-1.19 MPa， 高宽比为 6 的结构， 最大面压为 28.2 MPa， 最小面压为 0.59 MPa。 所以可以确定， 该结构的最大高宽比在6～7 之间， 因此剪力墙结构的高宽比限值建议不宜大于7。

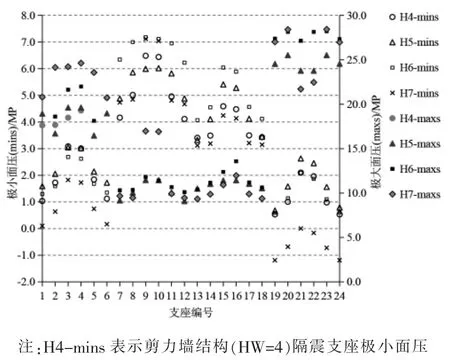
图18 Y 向地震作用下不同高宽结构支座面压Fig.18 Compressive stress of isolation bearing with different aspect ratios under Y direction earthquakes

图19 支座最小面压变化趋势Fig.19 The changing trend of minimum compressive stress of isolation bearing

对比不同高宽比隔震结构支座最大面压和最小面压， 结果如图19 所示。 可以看到支座最大面压随结构高宽比的增加呈增大趋势。 随高宽比的增加， 支座最小面压没有呈现连续递减的趋势。在 X 向地震作用下， 高宽比为 4、 5、 6 的隔震结构支座最小面压随高宽比增加而变大， 支座受拉的可能性降低。 由此可知， 基础隔震结构高宽比的增加， 隔震支座更容易因短期最大面压超限而破坏。

5 结论

本文对框架和剪力墙结构的高宽比限值进行研究分析， 可以得出如下结论

（1）高宽比为4 的框架结构采用基础隔震后支座拉应力已经超限， 而剪力墙结构的隔震支座尚未出现拉应力。 说明规范规定的高宽比限值仅适用于剪切变形的结构， 不适用弯曲变形以及弯剪变形的结构。

（2）强震下框架结构的隔震支座其拉应力更易超限， 而剪力墙结构的隔震支座其压应力更容易超过限值。

（3）剪力墙结构高宽比限值不宜大于7， 随结构高宽比的增大， 隔震后结构周期的延长效果降低。 结构减震系数随高宽比的增高有所增大， 但以弯曲变形为主的基础隔震结构， 减震系数受结构高宽比的影响不大。