基于无人机摄影测量技术研究有无地面控制点的差异性在地震方面的应用

刘 超， 杜 鹏， 王 银， 余思汗， 杨 顺

（宁夏回族自治区地震局， 银川 750001）

0 引言

近年来空间物体的三维模型重建成为数字摄影测量和计算机视觉领域的研究热点[1-2]。 目前三维模型重建的方式主要有两种， 一种是基于三维激光扫描， 一种是基于数字图像。 前者激光雷达扫描（LiDAR， Light Detection And Ranging）技术迅速发展， 将激光测距、 惯性导航和全球定位3 种技术相结合， 直接获取高精度三维模型[3-5]， 但仪器价格昂贵、 操作专业、 数据处理复杂致使普及率不高、 广泛应用受限[6]； 后者通过匹配被测物体不同数字图像中的同名点， 交汇得到空间点的三维空间坐标[7-9]， 这种名为 SfM（Structure from Motion）三维重建技术获取的三维模型分辨率和精度与LiDAR 相当[10-11]， 但测量成本低、 操作灵活快捷、数据处理简单， 已被应用于地震领域的多个方面[12-16]。

基于SfM 算法进行影像数据处理时， 通过图像特征匹配与跟踪解算出相机的空间位置， 然后计算出三维密集点的相对坐标， 其只具有图像的空间坐标系， 如果要转换成现实世界的空间坐标系， 则需要用少量地面控制点（GCP，Ground Control Point）进行空间校正才能得到现实中精准的水平位置和垂直高程。 然而， 要通过野外测量（如利用差分GPS）获取现实空间坐标并在数据处理时加入控制点， 则需要更贵的仪器、 更繁的操作和更多的时间， 在地震应急现场恶劣的环境条件下， 人员是无法到达震中破坏严重的区域去获取控制点的， 即使是能够获取控制点在数据处理时耗时太多， 也无法快速完成影像数据的拼接和分析， 那么也不能及时地获取灾害情况为震后救援和重建提供科学依据。 因此本文针对有无控制点建立的空间坐标系误差大小能否满足不同方面的应用这一关键问题， 通过实例定量分析有无控制点相机位置的精度， 明确两种情况下处理结果在水平位置和垂直高程上的差异性， 结合实际应用的需要， 探讨不同情况在地震不同方面的发展前景[17-18]。

1 获取影像数据和控制点

本次使用精灵Phantom 4 四轴飞行器， 其搭载大疆公司制造、 焦距3.61 mm、 光圈f/2.8 自动对焦的FC330 型号相机， 配备1 英寸有效像素1240万的影像传感器， 保证了影像分辨率高、 畸变小及感光度强的特征。 该无人机集成了GPS/GLONASS 卫星定位双模块， 悬停精度在GPS 定位正常工作时垂直误差±0.5 m、 水平误差±1.5 m， 但悬停范围在0～10 m 导致测量时相机位置误差范围在0～10 m 甚至更大。 为了获取高精度的现实空间坐标， 使用 Trimble R8 差分 GPS 进行实测， 测量精度水平误差在±10 mm+1ppmRMS、 垂直误差在±20 mm+1 ppmRMS 的范围， 有效保证水平位置和垂直高程绝对值的精度在厘米级。

实例1 选择在宁夏回族自治区境内天景山活动断裂带西段， 古地震[19-20]造成的断层陡坎附近（图1）， 晴朗弱风天气环境保证飞行安全和稳定，阳光充足保证地貌光学特征显示最佳。 自动飞行软件设置飞行高度50 m、 重叠度航向和旁向均为80%， 覆盖区域为 200 m×200 m， 耗时 10 min 左右完成， 共获取28 张影像照片； 控制点在飞行区域均匀布设了10 个， 能够很好的约束相机位置有效避免影像数据扭曲变形。

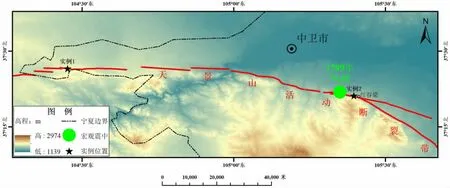
图1 实例位置及区域地震构造图Fig.1 Example location and regional seismotectonic map

2 影像数据处理

影像数据需要选择集成SfM 算法的软件进行处 理 ， 如 Pix4Dmapper、 PhotoScan、 Smart3d、PPSG 及 SFMToolkits 等[15，21-22]， 本文选用 PhotoScan软件， 处理流程如图2 所示。

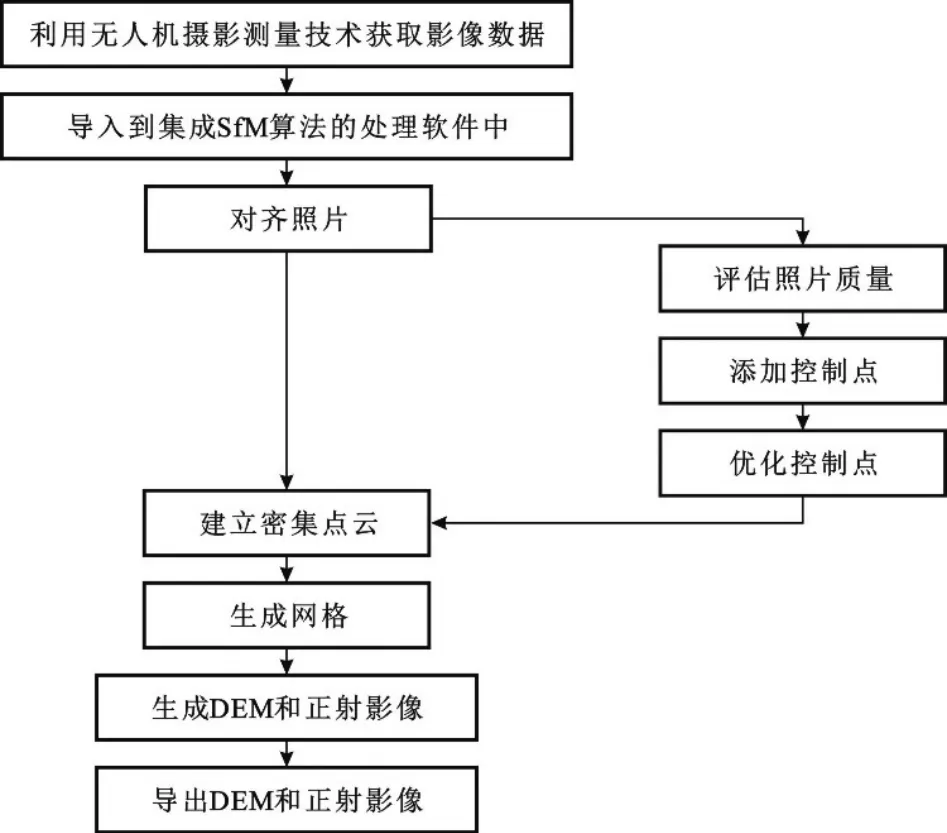
图2 影像数据快速处理（左）及高精度处理（右）流程Fig.2 Fast processing（left） and high precision processing（right） of image data

在快速处理流程中（图2（左））， 不进行照片质量评估和控制点校正， 直接利用SfM 算法解算出相机位置和姿态， 重建三维模型生成密集点云；在高精度处理流程中（图2（右））， 需要评估照片质量， 将评估参数低于0.5 的照片剔除， 然后在高质量照片上添加控制点， 进行坐标的绝对校正， 将三维点的图像坐标系转换为世界空间坐标系， 获得具有真实空间坐标系的密集点云。 后续基于生成的密集点云， 通过插值获取DEM 和正射影像。

2.1 无控制点快速处理

软件在无控制点的情况下为快速处理， 耗时1小时左右， 其结果中平均飞行高度49.7 m， 摄影覆盖面积约17 100 m2， 解算出的相机位置如图3a（黑点表示相机位置）， 图中照片区域覆盖度在9张以上的占比超过60%， 平均有效重叠约为5.9次， DEM 分辨率 3.77 cm/pix， 点云密度 702.808点/m2， 高程范围 1856～1873 m（图 4a）， 高程差 17 m， 正射影像分辨率 1.89 cm/pix（图 5a）。

PhotoScan 软件会估算相机内部参数比如相机位置和地面控制点， 这就为定量分析有无控制点相机位置的精度提供了可行的途径。 相机位置总误差的计算公式如下：

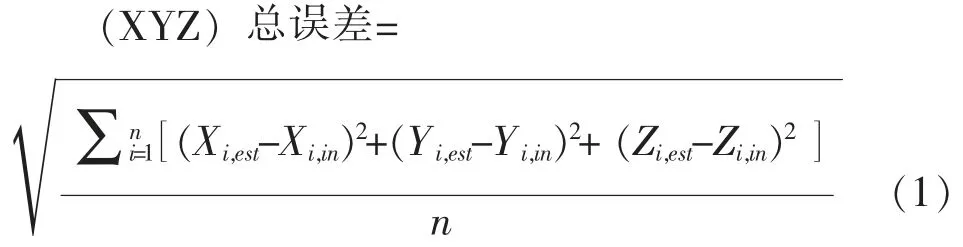
Xi，est： 第 i 个相机位置的 X 坐标估计值

Xi，in： 第 i 个相机位置的 X 坐标输入值

Yi，est： 第 i 个相机位置的 Y 坐标估计值

Yi，in： 第 i 个相机位置的 Y 坐标输入值

Zi，est： 第 i 个相机位置的 Z 坐标估计值

Zi，in： 第 i 个相机位置的 Z 坐标输入值

由公式（1）得到无控制点情况下28 张照片相机位置的总误差为 0.95 m（表 1）， 其中 X 误差为0.43 m、 Y 误差为 0.41 m、 Z 误差为 0.74 m 及 XY误差为0.59 m， 每张照片相机位置和误差估计值见图6a。

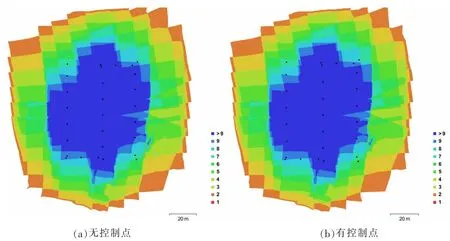
图3 有无控制点解算的相机位置及照片覆盖度Fig.3 Camera locations and image overlap with or without GCPs

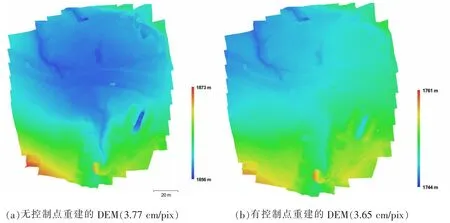
图4 有无控制点重建的DEMFig.4 Reconstructing DEM with or without GCPs

图5 有无控制点重建的正射影像及控制点位置Fig.5 Reconstructing orthomosaic with or without GCPs and GCP locations

表1 相机位置精度检验结果Table 1 The accuracy check results of camera positions

图6 相机位置和误差估计值Fig.6 Camera locations and error estimates

2.2 有控制点高精度处理

软件在有控制点的情况下为高精度处理（10 个控制点的位置见图5b）， 耗时5 h 左右， 其结果中平均飞行高度49.7 m， 摄影覆盖面积约15 800 m2，解算出的相机位置略有变化见图3b（黑点表示相机位置）， 图中照片区域覆盖度在9 张以上的占比也超过 60%， 平均有效重叠约为5.9 次， DEM 分辨率 3.65 cm/pix， 点云密度 749.434 点/m2， 高程范围 1744～1761 m（图 4b）， 高程差 17 m， 正射影像分辨率 1.83 cm/pix（图 5b）。

根据总误差公式（1）， 估算出了每个地面控制点的误差见表2， 最终得到了所有控制点的X 误差为 2.60 cm、 Y 误差为 2.31 cm、 Z 误差为 2.92 cm、XY 误差为 3.48 cm 及总误差为 4.54 cm， 均在 5 cm 的范围内。 通过地面控制点的校正， 照片相机位置的误差明显增大 （图6b）， 结果见表1 有控制点列（数字加粗）， X 误差为 1.46 m、 Y 误差为 1.07 m、 Z 误差为 109.53 m、 XY 误差为 1.81 m 及总误差为 109.55 m， 可见水平位置 （XY）误差＜2.00 m，垂直高程（Z）误差＞100.00 m。

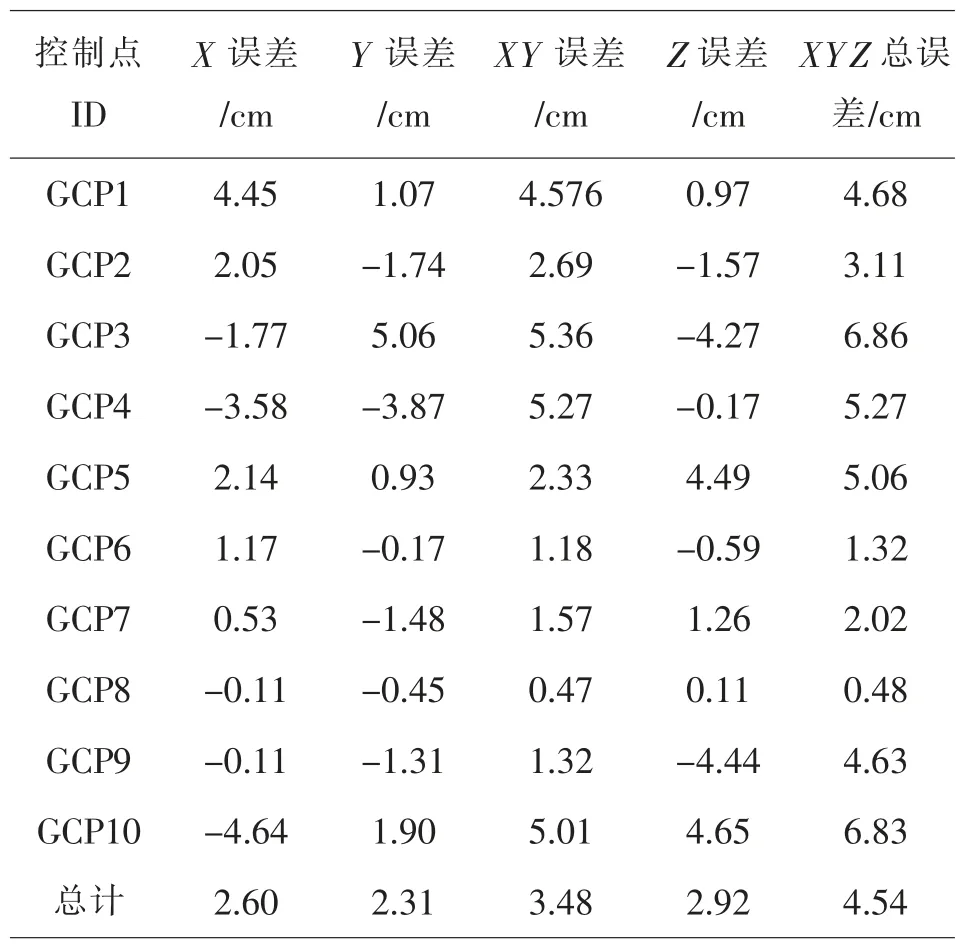
表2 控制点精度检验结果Table 2 The accuracy check results of GCPs

3 DEM 精度对比分析

3.1 利用地面控制点检验DEM 精度

软件利用SfM 算法精确解求出的相机空间位置，能够获取带有空间坐标系的三维密集点云， 然后采用插值的方法生成网格数据DEM， 其精度差异决定着分析地形地貌的结果。 汪思妤等（2018）利用地面控制点计算出均方根误差（RMSE，Root Mean Squared Error）来检查无控制点的情况下DEM 在水平位置和垂直高程上的精度[23]， 本文采用该方法， 在无控制点的情况下提取DEM， 计算出10 个点在X、 Y、 XY、Z 和 XYZ 的均方根误差， 结果见表 3， X 误差为 0.66 m、 Y 误差为 1.54 m、 Z 误差为 109.88m、 XY 误差为1.68 m 及XYZ 总误差为 109.89 m， 可见水平位置（XY）误差 1.68 m＜2.00 m， 而且利用 Trimble R8 差分GPS 测量的水平误差为±10 mm+1pp mRMS 及地面控制点本身的水平误差为3.48 cm（表2）， 则水平位置误差最大 1.73 m＜2.00 m； 但垂直高程（Z）误差＞100.00 m， 这与表1 中有控制点校正下相机位置的误差估计值相吻合， 说明没有控制点的情况下， 软件解求出的相机位置及获取的地形DEM 数据只具有图像空间坐标系， 无法转换到现实世界空间坐标系， 故其相机位置精度并不能代表DEM 的精度。 但增加了地面控制点后， 将相机位置进行了变换， 使得能够获取绝对空间坐标系的三维密集点云， 此时地面控制点校正了重建的DEM 数据， 故地面控制点的精度代表了有控制点的情况下生成的 DEM 精度[15]， 而相机位置的精度则代表了没有控制点的情况下相机位置的偏差， 进而影响并决定了生成的DEM 精度。

表3 无控制点的情况下DEM 精度分析Table 3 Accuracy analysis for the DEM without GCPs

3.2 利用等值线对比DEM 高程数据

对比2.1 和2.2 有无控制点的情况下生成的DEM 高程数据发现， 两种情况生成的DEM 高程范围分别为 1856～1873 m 和 1744～1761 m（图 4）， 高程范围均为17 m， 为了进一步探讨两种情况生成的DEM 在内部的高程差异， 利用Surfer 专业软件， 采用自然邻近插值的方法对高质量三维密集点云进行插值生成网格数据DEM， 网格大小均为176 行×200 列， 节点总数 35 200 个， 用无控制点减掉有控制点的网格数据DEM， 得到新的高程差网格等值线图（图7）， 可以看出， 高程差主要集中在 108～113 m， 平均高程差 110.51 m， 这与 3.1 无控制点的情况下DEM 垂直高程误差（Z）109.88 m接近， 说明与利用地面控制点检验DEM 精度的结果相吻合； 图7 中高程差并非唯一值， 而是由中心向外逐渐增大的同心圆， 中心向东偏移， 相邻等值线高程差为0.5 m 则相邻等值线之间的区域内相对高程差＜0.5 m， 说明在局部范围内的相对高程值的误差＜0.5 m。

3.3 有无控制点的差异性

基于以上有无控制点的处理结果， 通过对比分析影像数据获取、 处理和精度， 将两者的差异性总结如下。

（1）数据获取： 无控制点数据获取简易、 快速， 设备成本低， 只需要一台无人机硬件和自动飞行软件， 选择能够起飞无人机的某一点即可获取整个研究区域的影像数据， 并不需要人员去研究区域的所有地方， 全程1 名人员就可完成。 有控制点数据获取除以上设备外， 还需要测量地面控制点的硬件设备如差分GPS， 其不仅价格昂贵，而且野外操作复杂； 在布设控制点时需要人员放置在研究区域合适的位置， 这就需要踏勘整个研究区后进行选择； 在测量控制点时至少需要2 名人员才可完成。 装卸设备和测量时需要投入更多的人力， 耗费大量的时间， 获取影像数据复杂、费时且技术要求高。

图7 高程差网格等值线图Fig.7 Contour map of elevation difference grid

（2）数据处理： 无控制点数据处理快速， 数小时之内就可完成， 且自动化程度高， 批量处理操作简单， 不需要人员投入更多的时间就可获得最终的DEM 和正射影像。 有控制点数据处理过程复杂、 技术要求高， 尤其是在用地面控制点校正相机位置时， 不仅要消耗大量的时间， 而且需要熟练的操作和丰富的经验才能将控制点放置在最佳的位置， 使误差降到更低以达到更高的精度， 该过程无法进行自动化处理只能通过人工操作完成；随着研究区面积的增大， 需要布设的控制点增多，数据处理的工作站配置要求更高， 成本就越高，耗费的人力就越多， 这种情况下至少需要2～3 d 才能完成。

（3）精度检验： 这两种情况下， 基于高密集点云 （＞700 点/m2） 生成 DEM 和正射影像的分辨率基本不受影响， 均在厘米级， 这说明了有无控制点不会影响图像的分辨率， 但能够影响三维密集点云的坐标。 无控制点时由于软件中没有控制点校正， 缺乏真实世界绝对空间坐标的参考， 使得软件处理时相机位置的精度无法代表DEM 的精度， 通过地面控制点对DEM 的检验结果表明水平位置误差＜2.00 m， 垂直高程的误差＞100.00 m， 但通过高程差的等值线分析在局部范围内的相对高程值的误差＜0.5 m， 所以在基于DEM 提取活动构造定量参数中的垂直位错量时， 由于其为剖面上的相对高程值， 那么在有无控制点的情况下提取结果的米级数值是相同的； 由此可见无控制点情况下快速提取活动构造的垂直位错量误差＜0.5 m。另一个方面， 具有现实世界空间坐标系的控制点误差均在5 cm 的范围内， 由此约束和校正后的密集点云具有真实空间坐标系， 生成的DEM 和正射影像不仅在图像分辨率上达到了厘米级， 而且在空间绝对位置上偏差＜±5 cm， 精度较无控制点提高了至少数十倍。

4 有无控制点在不同方面的应用

从第2、 3 节的分析中可以看出， 在有无控制点的两种情况下数据获取、 处理和精度各有差异和优缺点， 将此对比结果与目前地震领域的研究相结合， 本节探讨了两者在地震不同方面的应用前景。

4.1 无控制点

在无控制点的情况下， 数据获取简易、 快速、成本低， 数据处理时间短、 技术要求低、 自动化程度高， 生成的DEM 和正射影像分辨率在厘米级， 但精度在米级， 水平位置误差＜2.00 m， 垂直高程绝对值误差超过100.00 m 但在局部范围内的相对高程值的误差＜0.5 m， 适用于快速获取影像数据和分析， 在地震应急现场可自动快速完成拼接并获取高精度震后影像资料， 在短时间内为灾情评估提供宏观震中的灾害信息。 若发生6.5 级以上的地震会产生地表破裂带[24]， 在地表遗留下地震沟槽、 线性陡坎、 断错水系冲沟及地表裂缝等形变地貌[25-26]， 记录着断裂带的活动信息， 尽快地获取这些地貌数据能够提取到地震活动相关的构造参数， 为地震危险性评估提供科学的依据。 在大地震发生后恶劣的环境条件下， 人员无法到达破坏严重的发震构造区， 因此只能在无控制点的情况下利用无人机快速获取地震地表破裂带附近的影像数据， 其简易、 快速、 安全和自动化程度高的优点展现出了在地震应急现场和救援中良好的应用前景和巨大的应用潜力。 虽然该方面还处在探索阶段， 但相信通过更进一步的研究和发展， 无人机技术会在地震应急中发挥出更大的作用和价值。

实例2（图1）以1709 年宁夏中卫南的7?级地震为例， 选取震中红谷梁西具有地震陡坎和断错水系冲沟形变遗迹[25-27]的附近， 在无控制点的情况下获取该处影像数据， 经过第2 节相同步骤的处理， 获得了6.33 cm/pix 分辨率的DEM。 在确定了断裂的方向之后， 在同一地貌上提取出垂直于断裂方向上的地形和坡度数据 （图8）， 图中上方为测量的图解[15，28-29]， 利用坡度快速分离出上、 下盘， 然后拟合出上、 下盘的直线L1和L2获得陡坎范围内上、 下盘间的高程差 h1和h2， 最后求得平均值 h代表断层陡坎的高度， 并计算测量误差dh。 由此可见陡坎垂直位错量为相对高程差非绝对高程值，故无控制点的情况下垂直位错量的误差为＜0.5m 并非绝对高程值误差（＞100.00 m）。 另一方面， 在DEM 基础上提取水平位移量时， 需要确定位移标志物如沟心和沟壁的趋势线[30]然后进行测量， 因此无控制点的情况下水平位移量误差为＜2.00 m。

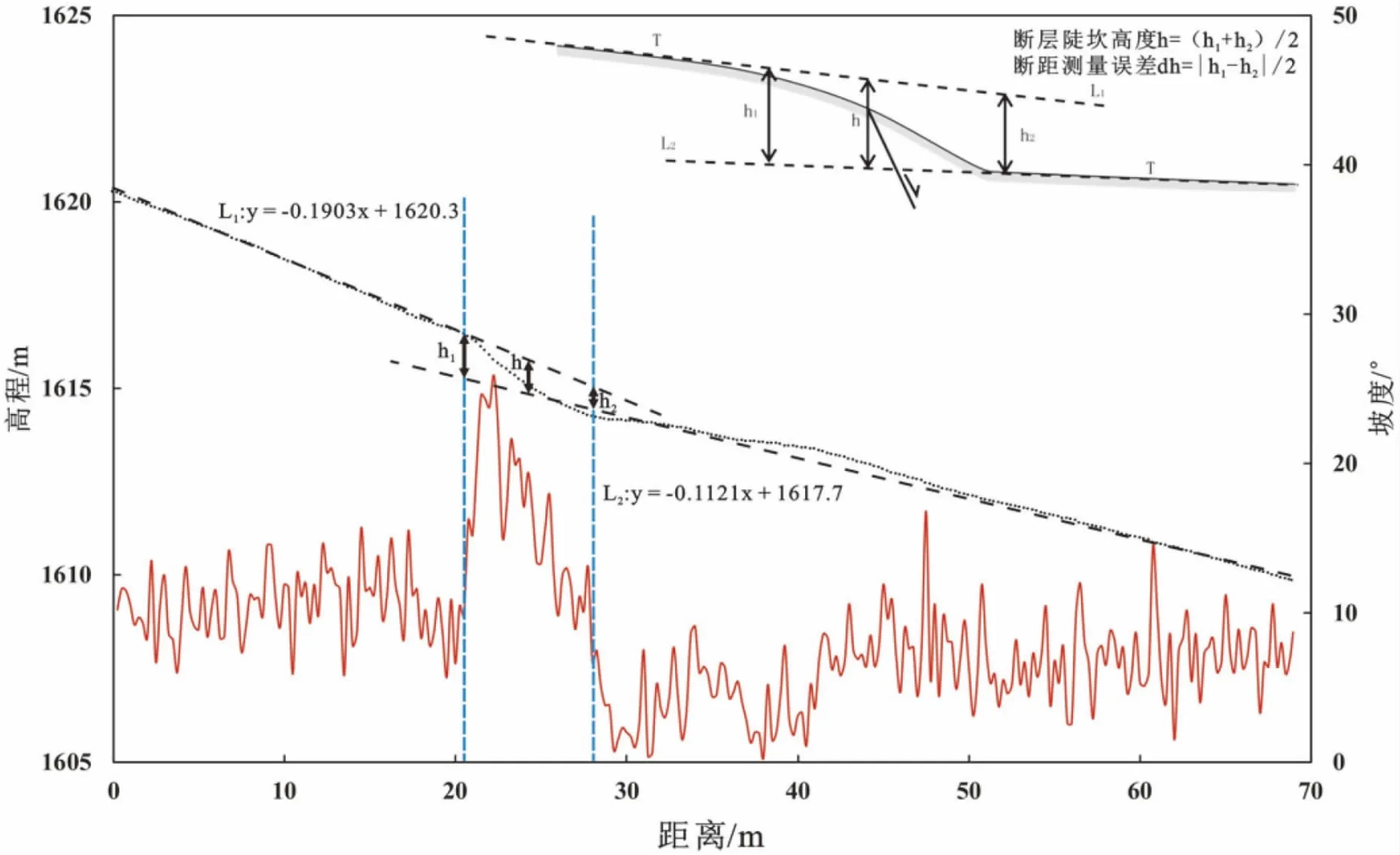
图8 地形和坡度剖面确定的垂直断错量（h）Fig.8 The vertical fault value（h）extracted by the topography and slope profile

4.2 有控制点

在有控制点的情况下， 虽然数据获取、 处理具有成本高、 操作复杂、 处理时间长、 自动化程度低且技术要求高等诸多不便因素， 但生成的DEM 数据具有厘米级的超高分辨率和＜5 cm 的超高精度， 这一优势使得该方法被广泛应用到地震地质学研究中。 如活动构造定 量研 究[11，15，31-32]和微地貌精 细 解 译 及 分 析[6，16，33]， 展现出了广阔的应用前景， 已成为该方面研究中一种重要的新技术手段， 前人研究成果丰硕本文就不再举例赘述。 虽然这方面应用还存在一定的局限， 如测量区面积有限、 植被覆盖区效果不理想及受天气影响较大等问题， 但相信随着技术的发展和提高影响因素会越来越少， 该方法会有更大的价值和意义。

5 结语

本文通过对比有无控制点情况下， 数据获取、处理和精度的差异性， 明确了在无控制点的情况下数据获取和处理简易、 快速且成本低， 水平位置误差＜2.00 m， 垂直高程绝对值误差超过100.00 m 但在局部范围内相对高程值的误差＜0.5 m； 在有控制点的情况下数据获取和处理复杂、 费时且成本高， 但有＜5cm 的高精度， 两者均可生成厘米级分辨率的DEM 和正射影像。 基于两种情况的优劣势， 前者在地震应急中展现了良好的应用前景和巨大的应用潜力， 并且可以快速、 定量提取发震构造的变形参数， 垂直位错量误差＜0.5 m、 水平位移量误差＜2.00 m； 后者在活动构造定量研究和微地貌精细解译及分析中展现了广阔的应用前景，提取活动构造的定量参数误差＜5 cm， 其优势在精细化、 定量化研究中得到了充分地发挥。