NLLoc 定位方法在福建地区的适用性探究

张丽娜， 张红才， 巫立华， 段 刚， 戴丽金， 廖诗荣

（福建省地震局， 福州 350003）

0 引言

地震定位是地震学中基础问题之一， 也是地震台网的基本任务之一。 地震定位结果对于震源几何构造的研究、 地壳应力场分析等具有重要的意义。 快速准确的地震速报并产出地震目录， 也可为地震应急救援、 震后减灾和救灾及震后地震趋势预测等提供基础数据[1]。 地震定位包括确定震源位置和发震时刻， 其精度受到定位方法、 地壳速度模型等诸多因素的影响。 地震定位方法研究及地震定位精度的提高， 一直是地震学研究的基本课题。

2000 年， Lomax 等[2]研究学者提出一种非线性搜索定位方法 NLLoc， 并开发了地震定位程序NonLinLoc（http：//alomax.free.fr/nlloc/）。 Stephan[3]利用NLLoc 定位方法对中国台湾黄石国家公园地区的25 267 个地震事件重新定位， 与原始地震位置相比， 重新定位的位置条带状分布特征更明显。Yavor 等[4]采用NLLoc 定位方法对加利福尼亚南部地震事件进行定位， 进而对该地区活动断层特性等进行探索。 Theunissen[5]等研究指出三维速度模型能够更好地解决深度定位问题， 尤其是在台网边界地区 （如间隙角大于180°和首台距离大于15 km）， 并且采用等时差 EDT 的 NLLoc 定位方法，给出震源参数及其误差分析。 Antonino[6]应用NLLoc方法分析了台站位置分布对定位震源位置质量的影响， 指出NLLoc 方法是一个快速有效的自动定位方法， 即使使用较少的地震震相， 定位结果仍然可靠有效， 且该算法对到时中的噪声影响并不敏感。 区别于标准的三维线性迭代法， NLLoc 方法还给出了位置不确定性分析和解析度信息。 韩雪君[7-8]也简要介绍了NLLoc 定位方法， 并将八叉树搜索方法应用于预警的三维实时定位中， 能够快速给出震源在三维空间的可能位置。 可见， 该方法有望大幅改善地震定位精度。

本文利用 “福建及台湾海峡深部构造海陆联测” 项目实施的22 次人工爆破事件记录和88 次福建仙游震群序列M≥1.5 级地震事件记录， 应用NonLinLoc 地震定位程序重新定位， 检验NLLoc 方法在福建台网地震定位中的适用性。 为方便与现有定位算法进行对比， 本文定位中同样采用华南地区一维速度模型[9]， 如表1， 并将其网格化为三维速度模型进行使用， 输入相关震相文件， 进行重定位， 将其重定位结果与台网常用定位方法（Hyposat、 HYP2000、 LocSAT 和单纯型）作对比，并对该方法定位结果的可靠性进行分析。

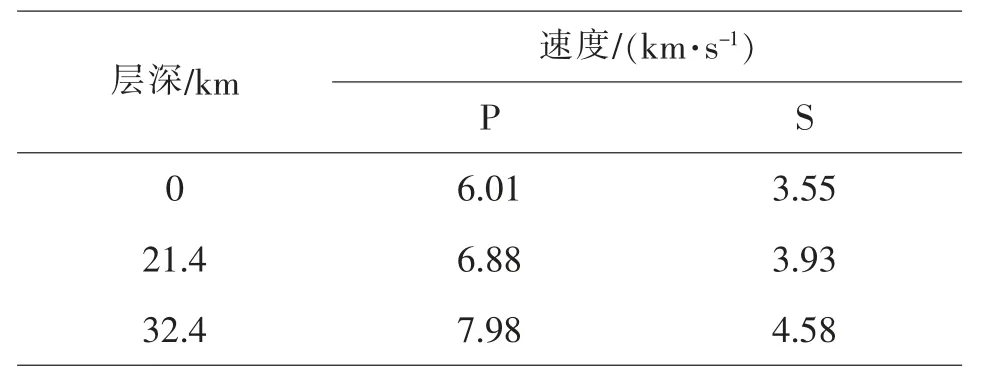
表1 华南模型Table 1 South China model

1 定位方法简介

1.1 NLLoc 方法及主要算法

地震定位方法NLLoc 是一种基于三维速度模型的非线性搜索定位方法， Lomax 开发的定位软件NonLinLoc 能够产出欠拟合函数、 震源位置和边际后验概率密度函数估计（如式 （1））。 该程序基于Tarantola 等[10]的反演方法以及 Tarantola 等[10]、 T.J.Moser 等[11]和 Wittlinger 等[12]的地震定位方法。 假设震相到时观测误差（震相拾取误差）和理论走时误差符合高斯分布， 在给定的观测到时和由观测台站和空间网格点计算出的理论走时， 这个假设能够计算发震时刻的最大概率值。 四维的地震定位问题就转化为三维空间的网格搜索问题。

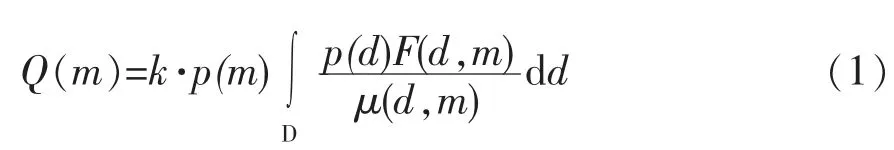
式（1）中， k 为归一化常数， D 为数据空间， d∈D， p（d）为概率密度函数， p（m）代表震源位置参数向量 m 的先验概率密度函数， F（d，m）为正演问题的概率密度函数， μ（d，m）通常设为均匀分布。 该式的积分项一般称作似然函数， 记为L（m）。 假设观测数据的概率密度函数p（d）为高斯分布， 均值为d0和协方差矩阵为Cd， d 和m 的不确定性是可忽略的且是相互独立的， 则 μ（d，m）=μ（d）·μ（m)，其中μ（d）通常被认为是常数。 通过简化， 似然函数可定义为：

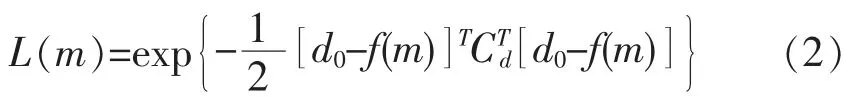
NLLoc 方法中采用等时差（EDT）格式[13-14]的似然函数， 当出现异常值时， 该格式是稳健的。 在等时差情况下， 该似然函数可简化为：

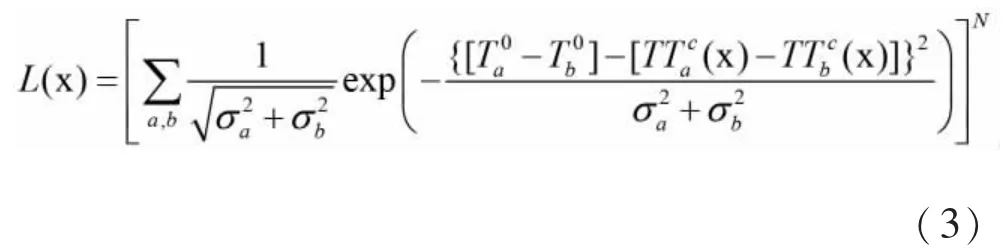
式（3）中， X 是m 的空间上分量； 对于两个观测台站，是观测到时，是理论走时； σa和σb是观测到时和理论走时的标准差。

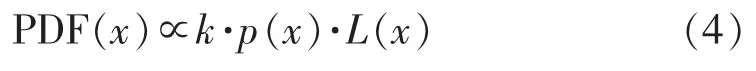
1.2 八叉树搜索算法

NonLinLoc 程序中， 其搜索方法有多种选择，如八叉树法、 网格搜索法等， 本文选择八叉树搜索法进行定位。 八叉树搜索法在三维空间中使一种准确、 高效的全局搜索法， 对产生的样本细胞不断递归细分。 首先， 初始化一个给定的空间，计算每个网格中心点的概率值， 将其概率值放置有序列表LP中， 接着将概率值最大的点剖分成8个子细胞， 计算8 个子细胞的概率值并继续放入概率列表LP中， 然后， 从列表中选出概率最大点再次剖分， 再次循环， 直到满足给定的终止法则。这是一个快速收敛的递归过程， 比网格搜索法快，比模拟退火法和遗传算法更具有全局性， 但缺点是依赖于初始网格大小和初始点。

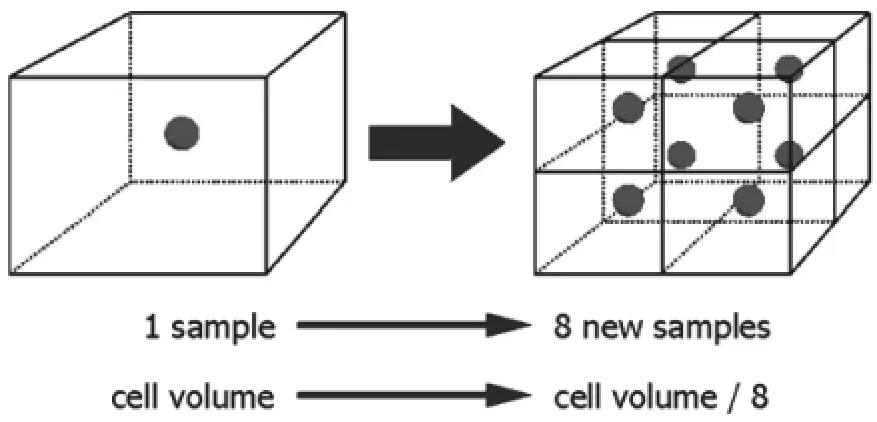
图1 八叉树搜索采样单元（http：//alomax.free.fr/nlloc/）Fig.1 Oct-tree searching method sampling cell

每个细胞中震源位置的概率计算近似如下：

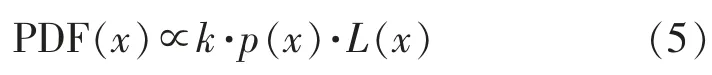
式（5）中， Vi是单元体积， xi是细胞中心坐标。

1.3 NonLinLoc 主程序简介

NonLinLoc 主程序定位流程图如图2（此流程图仅示意NonLinLoc 部分产出结果）， 首先， 输入一维（1D）速度模型或三维（3D）速度模型生成一个三维网格速度文件， 进而计算三维网格走时文件；走时文件可产出走时图， 亦可对给定的震源位置Time2EQ 模块计算预测走时； 输入事件的震相文应用NLLoc 模块定位， 即可寻找最优的震源位置和发震时刻， 并产出结果文件和结果展示图。

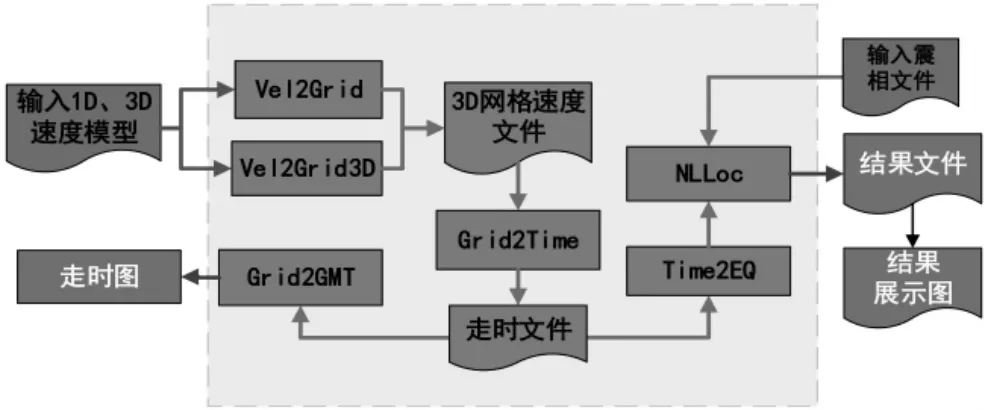
图2 NonLinLoc 主程序流程图Fig.2 The flow chart of NonLinLoc main program

1.4 福建台网常用定位方法

福建台网中心目前采用Jopens 系统MSDP 软件作为地震定位软件， 进行台网地震速报和地震编目等工作。 福建省常用的网内及网缘事件定位方法为： 单纯型、 Hyposat、 HYP2000 和 LocSAT等方法。

单纯型是利用基础数学上的单纯形搜索极值，达到终止法则如残差最小的理论模型作为震源位置， 该方法在极值附近收敛较慢， 对初始值比较敏感[15]， 适用于地方震、 近震和远震的定位程序。

HYP2000 和 Hyposat 都采用传统 Geiger 法的基本思路， 即观测方程组降维后直接用奇异值分解最小二乘法方程组， 实际计算中采用多种数据加权[16]。 HYP2000 可采用分区水平分层速度模型，可以为每个地震台站指定不同的速度模型， 定位起始位置均采用近台初值， 该法适用于网内震。而Hyposat 不仅可定位地方震和近震， 也可以定位远震， 其定位效果也相对较好。

LocSAT 采用传统Geiger 法的基本思路， 应用阻尼最小二乘法， 即将观测方程组化为正规方程组后用主元素消去法求解。 该法无法加权， 为了计算初值， 采用水平分层速度模型[17]。 该方法对于地方震、 近震及远震均可定位。

2 研究使用数据情况

2.1 22 次人工爆破事件

2010 年至 2014 年， 福建省地震局 “福建及台湾海峡深部构造海陆联测” 项目实施期间， 共进行22 次人工爆破激发实验， 激发时刻及震中位置信息见表2。

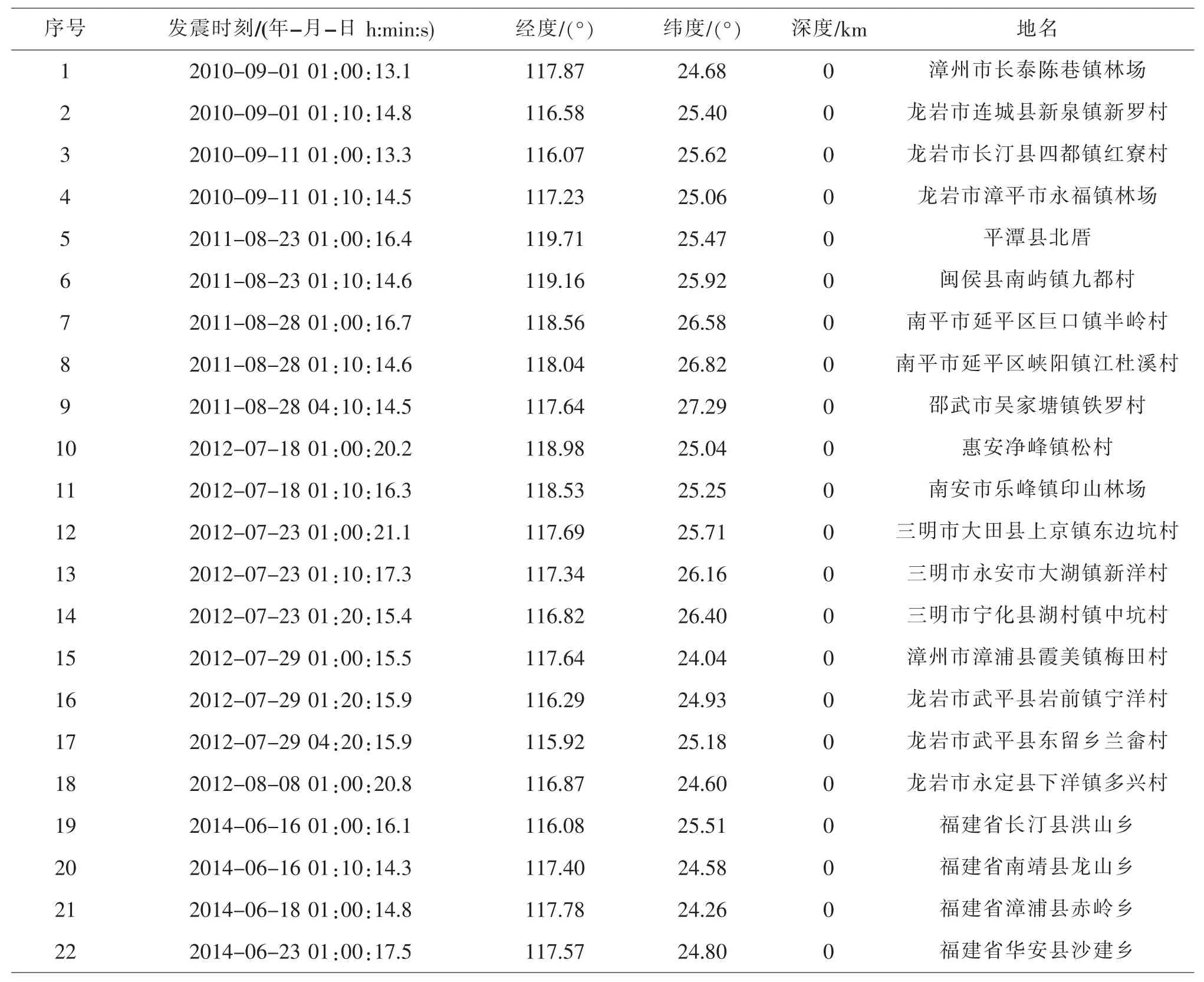
表2 22 次人工爆破信息Table 2 The catalogs of 22 explosions

本文利用这些人工爆破记录资料， 首先采用MSDP 软件进行分析。 由于震中距大于150 km 后大部分Pn 震相较弱， 到时位置拾取误差较大， 因此本文拾取震中距150 km 内的清晰震相 （主要震相为 Pn、 Pg 和少量 Sg）， 并剔除存在时钟误差的台站的震相数据。 随后， 分别采用目前福建台网常用的 Hyposat、 HYP2000、 LocSAT 和单纯型等四种定位程序及NLLoc 定位程序进行地震定位。 福建台网常用定位方法和NLLoc 定位程序采用的速度模型均为华南模型。 在定位事件时， Hyposat 定位可以设置自定义初始化选择和深度反演类型；该初始化选项中， 初始化深度设置为10 km， 初始深度误差设置为10 km， 深度计算设置为 “同时”；LocSAT 设置选项中， 初始深度设置为10 km， 深度计算设置为 “同时”， 迭代次数为： 40。

2.2 88 次M≥1.5 级仙游地震序列事件

本文选取2010-01-01—2019-09-01 福建仙游震群序列M≥1.5 级天然地震共88 个， 拾取震中距150 km 内的清晰震相， 并剔除存在时钟误差、断记等震相数据， 利用NLLoc 方法进行重定位，检验其定位天然地震事件的可靠性。

3 定位结果分析

3.1 22 次人工爆破重定位结果分析

3.1.1 定位震中误差分析

MSDP 自 带 的 定 位 方 法 Hyposat、 HYP2000、LocSAT、 单纯型和NLLoc 方法均使用华南模型，得到的地震定位结果震中分布如图3。 从表3 可见， 5 种定位方法中， NLLoc 方法定位震中误差为0.38±0.19 km， 结果最优； 使用 Hyp2000 方法震中误差均值0.72±1.09 km， 定位效果较差。 而单纯型和LocSAT 定位震中误差结果介于二者之间。

3.1.2 发震时刻误差分析

如图4 所示， NLLoc 方法发震时刻误差较小，为 0.35±0.13 s。 除了 HYP2000 定位法有 45.45%的事件发震时刻误差超过1s， 福建台网日常定位的其它方法发震时刻误差均值均在1s 以内。

3.1.3深度值分析

如图5 所示， 采用华南模型的NLLoc 方法深度误差最小： 0.75±1.62 km。 而 MSDP 自带的定位方法 Hyposat、 HYP2000、 LocSAT 和单纯型中， 其深度误差均值均超过2 km。 NLLoc 方法定位深度误差优于其它方法， 也表明该方法在定位事件深度上具有明显的优势。

3.2 88 次M≥1.5 级仙游地震序列重定位结果分析

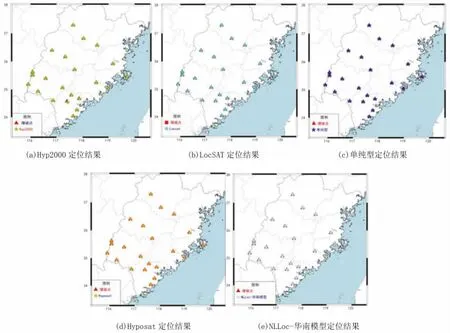
图3 5 种定位方法的震中位置图Fig.3 Epicenter location maps of the 5 location methods

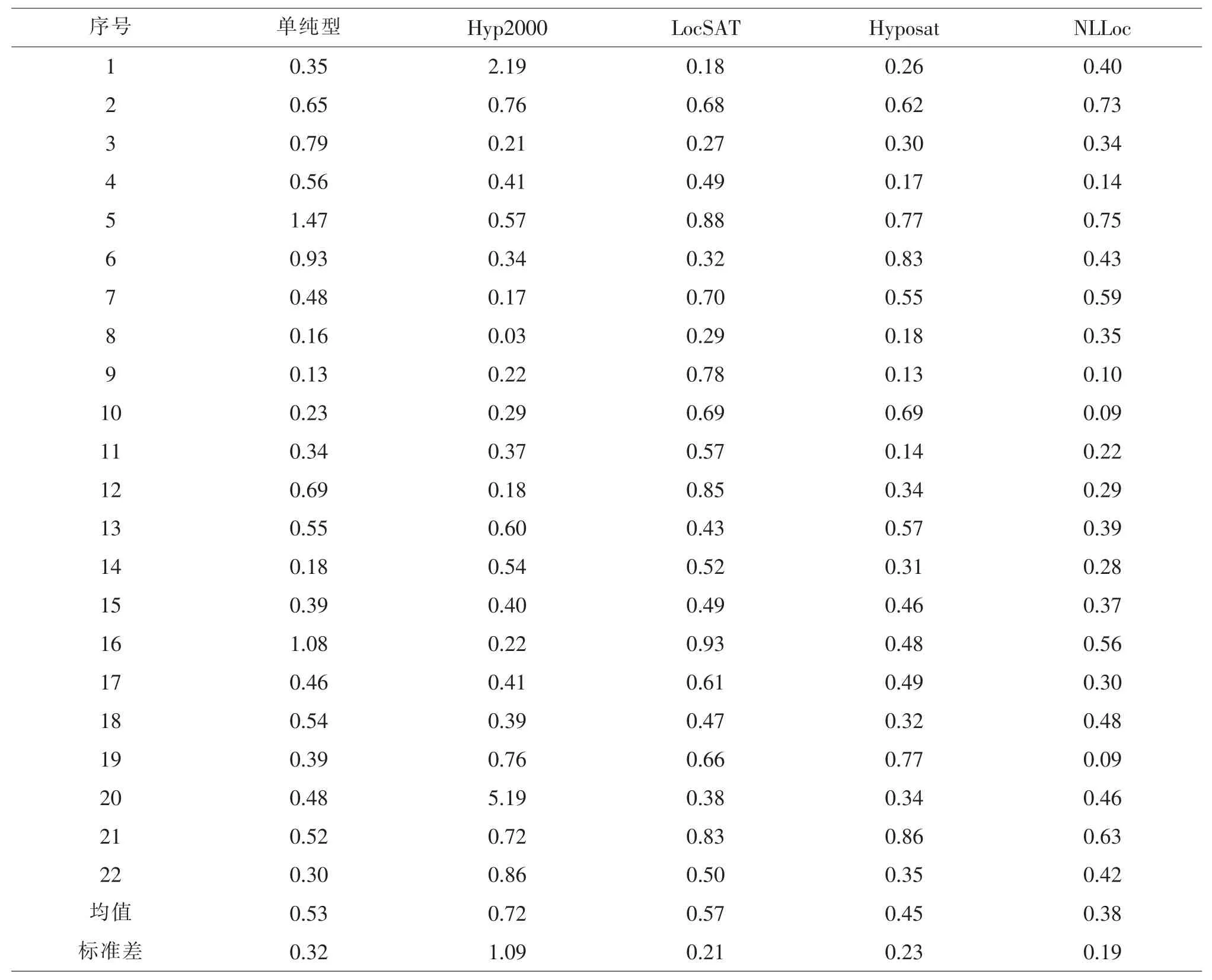
表3 震中误差值 （单位： km）Table 3 Errors of the located epicenters by 5 location methods （unit： km）

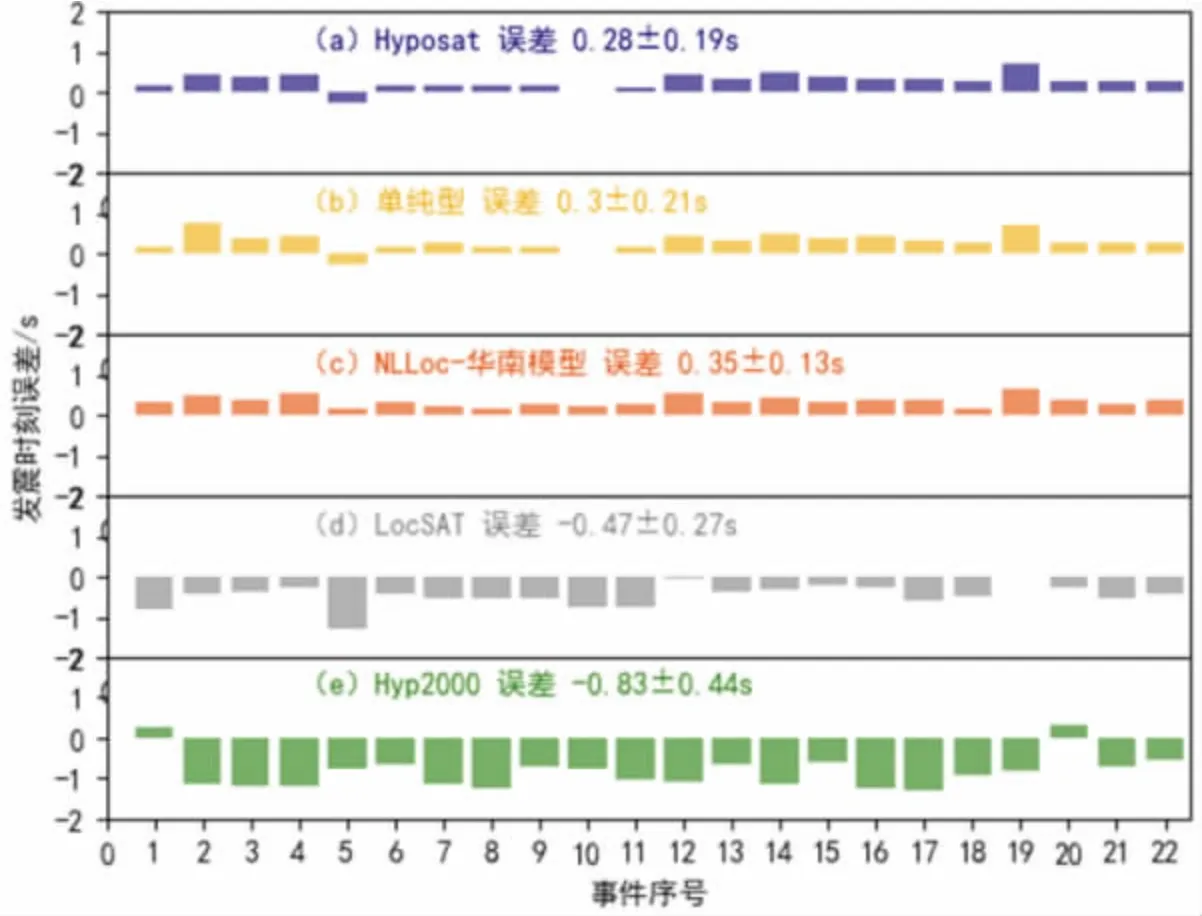
图4 发震时刻误差图Fig.4 Errors map of the origin time

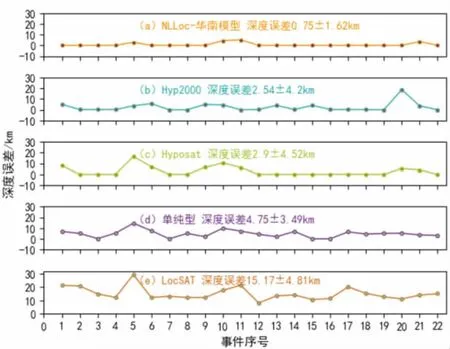
图5 深度误差对比图Fig.5 Comparison of the depth errors

通常天然地震震源深度比人工地震要深得多，天然地震波所通过的路径也复杂得多， 而人工爆破深度大多数为几米至几百米， 在地表岩层进行，其介质密度低， 爆破源是作用时间很短的点源瞬时膨胀力， 震源体积也相对小很多。 基于这些不同特征， 本文利用NLLoc 方法对88 次M≥1.5 级仙游地震序列重定位结果分析， 检验其定位天然地震事件的可靠性。

3.2.1 定位震中误差分析

如图 6， 截止至 2019-09-01， 序列活动在时间上存在丛集-平静的特征。 利用NLLoc 方法重定位， 仙游序列空间分布如图7， Ⅱ、 Ⅲ和Ⅳ三个时段地震主要呈北西向线性展布， 地震活动空间主体存在自北西向东南方向迁移特征， Ⅴ时段地震向西扩散， 主要分布在北西向线性展布。 该方法定位空间整体分布与袁丽文等[18]、 许振栋等[19]研究结果较一致。

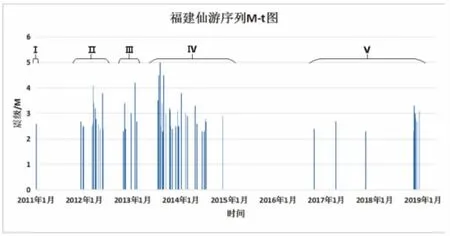
图6 福建仙游序列M≥1.5 级M-t 图Fig.6 M-t diagram of Xianyou earthquake sequence with M≥1.5

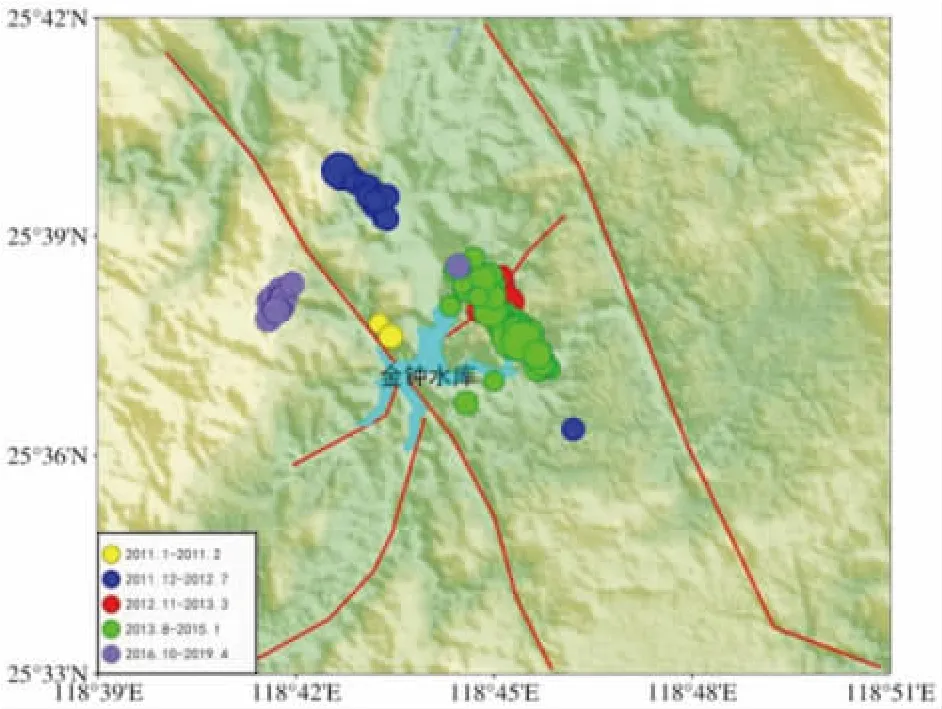
图7 仙游震群序列M≥1.5 空间分布Fig.7 Distribution map of Xianyou earthquake swarm sequence with M≥1.5

利用NLLoc 方法重定位结果与采用Hyposat 或单纯型定位的中国台网正式目录对比， 如图8， 震中误差为： 0.66±0.37 km， 有 2 个地震事件误差超过1.5 km， 分析这两个事件均为多个事件重叠，清晰震相少且台数少， 定位效果不佳。

3.2.2 发震时刻误差分析

重定位的发震时刻误差为： 0.16±0.15 s， 误差小。

3.2.3 深度值分析

在震源深度方面如表4， 利用NLLoc 方法重定位结果中， 地震序列活动初期深度较浅5 km 左右， 与李强等[20]利用 CAP 反演 2012 年 04 月 15 日4.1 级地震的震源深度4 km 一致， 但正式目录中，地震序列活动初期深度较深， 均值15 km 左右，与CAP 反演震源深度差值较大。 2012.11-2013.3逐渐加深趋势， 深度均值7.4 km， 2013 年8 月4.2级地震发生后， 地震震源深度分布稳定， 集中分布在 9 km 左右（如图 9）。

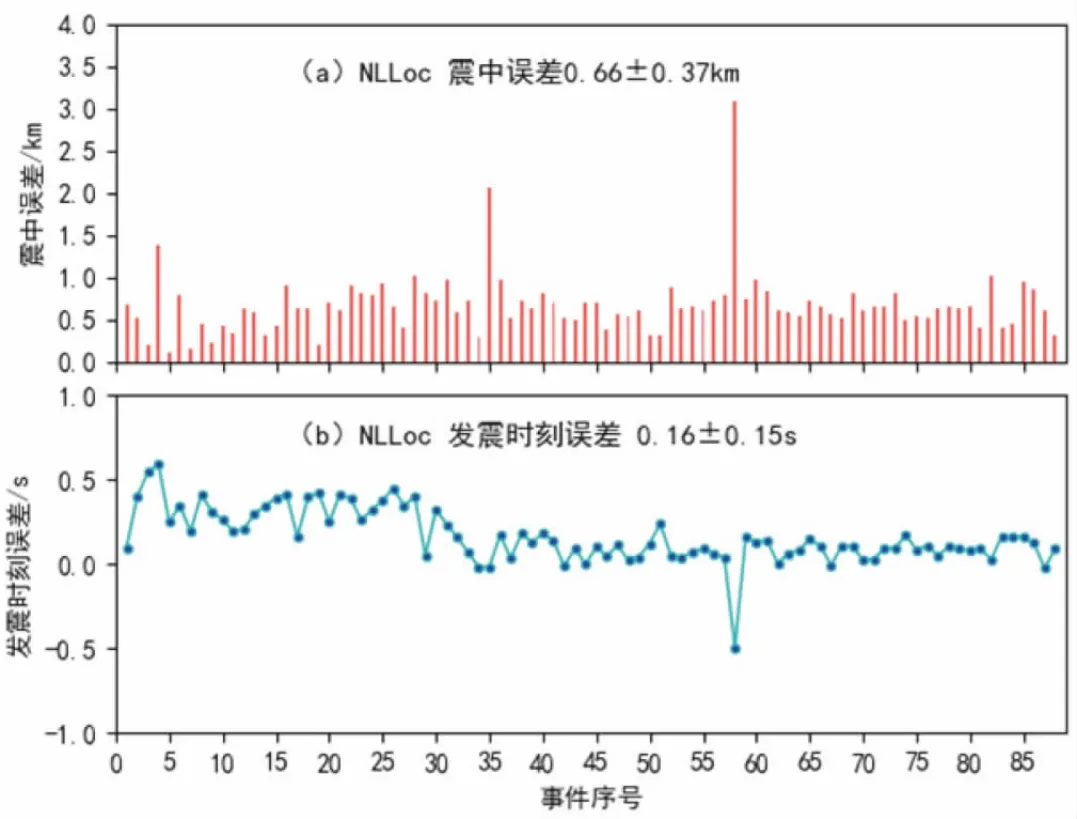
图8 福建仙游震群序列M≥1.5 震中误差和发震时刻误差图Fig.8 The epicenter error and origin time error of Xianyou earthquake swarm sequence with M≥1.5 in Fujian

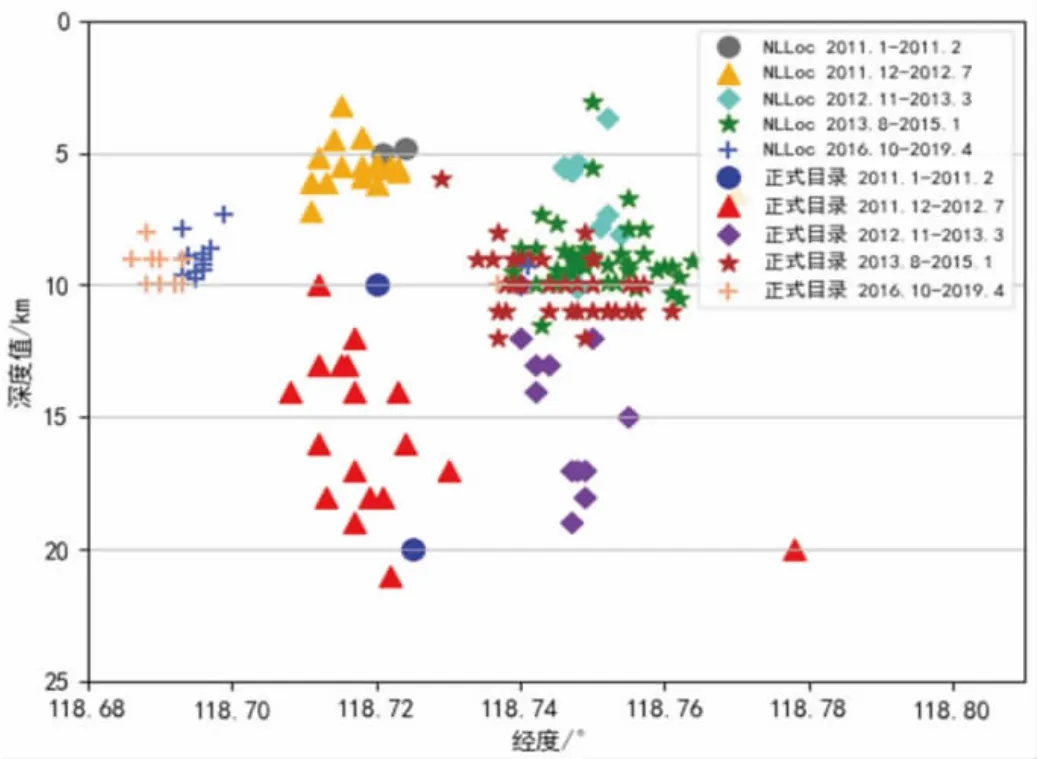
图9 仙游地震序列M≥1.5 深度时序图Fig.9 The depth sequence diagram of Xianyou earthquake swarm sequence with M≥1.5

表4 深度均值和标准差 （单位： km）Table 4 the mean and standard deviation of depth （unit： km）

4 讨论

本文利用三维非线性NLLoc 定位方法对 “福建及台湾海峡地壳深部构造海陆联测” 项目实施期间的 22 次人工爆破事件重新定位， 并与Hyposat、 HYP2000、 LocSAT 和单纯型这四种常用定位算法进行对比， 讨论了福建台网应用NLLoc程序测定人工爆破事件参数的精度问题。 研究结果表明， NLLoc 方法定位结果在发震时刻误差、 震中误差和震源深度误差等方面都优于现有定位方法结果， 尤其是在震源深度确定方面NLLoc 方法优势明显。 随后， 选取 2010 年 1 月至 2019 年 09月福建仙游震群序列M≥1.5 级共88 个天然地震，利用NLLoc 方法重定位， 与中国台网正式目录对比， 结果显示： 深度方面， 地震序列活动初期深度较浅， 逐渐加深趋势， 集中在 9 km 左右， 震中位置呈北西向线性展布； 但地震序列活动正式目录的深度初期较深， 与CAP 反演震源深度差值较大。

在震源深度方面， 如果某一台距离震中较近或就在震中区， 则该台震源距与震源深度相近[21]，根据震源距公式 D=Vφ×Δt， 其中 Vφ为虚波速度，Vφ=（VP*Vs）/（VP-Vs）， Δt 为该台的 S 波与 P 波到时差。 福建仙游序列事件中能记录到的最近台站为“福建仙游石苍台 （25.62°N， 118.74°E） ”， 震中距大约0.02°， 该台的震源距可近似为震源深度。 统计该台的观测记录， 获得到时差约为1.2s， 结合表1， 推算该台震源距为10.4 km， 则震源深度应略小于 10.4 km， 如图 9 所示， 利用 NLLoc 方法定位的震源深度略小于理论估值。 因此， 本文研究认为无论是人工爆破还是天然地震， NLLoc 方法有助于更好地确定事件深度， 有望提高台网定位精度。

此外， 还存在一些需要进一步讨论和研究的细节。 首先， 拥有已知发震时刻和绝对位置的爆破的数据量有限， 并且选取震中距150 km 以内的台站作为定位事件的界限仅仅是根据经验来确定：震中距在150 km 内， 震相较清晰， 参与定位台站数较多； 远台震相不清晰， 参与定位残差较大，有可能会影响NLLoc 定位效果。 第二， 对于网缘（网外）地震的定位问题尚未涉及。 本文的22 次爆破和福建仙游震群序列M≥1.5 事件均为陆上网内事件， 震中包围相对较好， 定位效果较好。 今后将有针对性研究网外事件， 进一步探讨该定位程序对该类事件的定位效果。 第三， 该定位方法输入三维速度模型时， 存在依赖于初始值的局限性，初始值偏离震中位置较远， 定位效果不佳。 若今后使用三维速度模型定位， 将解决依赖初始值的问题。

5 结语

通过本文研究结果表明， NLLoc 算法无论是人工爆破还是天然地震， 其定位结果在发震时刻误差、 震中误差和震源深度误差等方面都优于现有定位方法结果， 尤其是在震源深度确定方面NLLoc算法优势明显。 该法可用于台网日常地震定位，有助于更好地解决震源深度测定问题， 提高地震定位精度。 今后， 将进一步探究网缘（网外）人工爆破和天然事件的定位效果； 该方法为 “福建及台湾海峡深部构造海陆联测” 项目获取闽台三维地壳速度模型提供地震定位方法。