基于改进的层次分析法和接近理想点法的桥梁施工方案风险评价研究

■ 孙建诚 任浩 蒋浩鹏 张伟丁

1.河北工业大学土木与交通学院 天津 300401

2.大连海事大学道路与桥梁工程研究所 大连 116026

0 引言

桥梁工程的施工过程存在诸多风险，考虑工程进度中的风险类别，选择合适的施工方案可以避免因风险导致的施工延误，控制质量和施工成本，确保工期的顺利完成，可以有效的提高项目收益。施工方案受到不同层次的多个因素影响，信息复杂且各指标相互影响，传统的类比法等方式存在较多的主观因素[1]，因此，选择一个有效可行、客观合理的评价方法对桥梁施工方案风险进行评估具有重要的意义。

国内外学者对桥梁的评价工作做了大量研究工作。刘沐宇[2]等人根据层次分析法（Analytic Hierarchy Process，AHP）理论，将模糊综合评价方法应用到大跨度钢管混凝土拱桥的安全性上。魏翠玲[3]等人改进属性层次模型（Attribute Hierarchical Model,AHM）分析法，并与传统的层次分析法作比较。李远富[4]等将多目标模糊模型应用到铁路专业中去，利用该方法实现了在铁路选线设计中的最优方案。HANINE M[5]将综合模糊层次分析法运用到场地选址问题。Ying-Ming Wang[6]等提出了模糊接近理想点法（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）风险评估方法得出了非线性规划求解过程。

虽然各类评价方法更多的被应用到工程中，但我国对于桥梁的评价工作还处于初级阶段，对该方面的研究较少涉及。现在的研究中出现许多不同方法的综合评价，常用的有综合指数法、层次分析法、TOPSIS 法、灰色系统法等，根据不同因素影响，选择合适的评价方法会使得到的结果更加准确和科学。在已有的研究过程中，因为AHP 方法的简洁实用特点，多使用该方法用于桥梁、道路等工程风险评估中，但该方法受人为主观影响较大，且对方案排序要求较为粗略，需要结合其他方法综合应用。一般的TOPSIS 方法在评价不同问题过程中还存在其他问题，如权重为事先确定的，其值具有主观性；且此方法在应用中因新增方案而容易产生逆序问题等，需要对其进入更深入的研究分析。本文基于改进的AHP-TOPSIS法，改进TOPSIS方法使用的决策矩阵规范方法，简化理想方案和负理想方案，优化评价方法，针对桥梁施工中的四类一级风险和15个二级指标，建立了桥梁工程施工风险评价体系，采用AHP 和TOPSIS 法计算各指标权重，对各风险指标进行评价，建立最优决策模型，选择最优施工方案。

1 相关理论概述

1.1 层次分析法（AHP）概念

长期以来，由于许多施工问题经常需要考虑多个因素，并且要依靠专家的主观判断，选择关键因素的方法至关重要。层次分析法（AHP）在1980年由SAATY Thomas 提出来，该方法已广泛应用于多属性决策环境中，是用来处理复杂的经济、技术、社会政治问题的理论，用系统分析的方法，对评价对象依评价目的所确定的总目标进行连续性分解，得到各级（各层）评价子目标，并以最下层作为衡量目标达到程度的评价指标，然后依据这些指标计算出综合评分指数对评价对象的总目标进行评价，依照大小来确定所评价对象的优劣等级。该理论的目的是来统一现实中问题的模型，并通过优化分析消除现有的零散问题。

AHP 在问题中的应用需要经过层次设计和评估阶段两个阶段。由于许多判断都会出于主观，层次结构的设计及其评估需要实际案例的经验和知识。在构件层次结构时，决策者必须尽可能全面的表达问题，而且评估还会受到决策者的主观判断影响，即使两个决策者构成相同的层次结构，但会由于他们的不同判断导致不同的优先级权重。

评估阶段基于成对比较的概念。相对的比较层次结构中某个元素的重要性或对给定标准的贡献。通常层次结构具有目标、标准、备选方案3个层次。目标放在顶层，标准放在中层，根据给定问题的复杂性，标准可能有多个级别。通过成对比较确定标准的优先级，得出元素优先级或权重的相对度量标准，然后与每个标准对应最低级别的替代项进行比较，最后将标准级别和替代级别的优先级求和得出总分[7]。

1.2 层次分析法（AHP）原则

（1）分解原则：该原则要求构建层次结构，已获得基本元素。一种有效的方法是从总体目标依次向下进行选择。第一级别为目标层，第二级别为标准层，其次第三级别为次标准。在底层显示备选方案（如项目1、项目2、项目3）。随着问题的复杂性差异，决策层次相应进行变动。

（2）比较判断原则：该原则要求形成一个矩阵，对第二级元素相对于总体目标的相对重要性进行成对比较。SAATY 在1990年提出重要性量表，包括同等重要、中等重要、稍微重要、非常重要、极其重要5个等级。

（3）优先权综合原则：优先权重由第二层开始向下综合，由局部优先权乘以上一级相对应标准的优先权，再根据其影响的标准对一个层次中的每个因素进行加权。此计算为元素集生成复合优先级或全局优先级。

1.3 接近理想点法法

TOPSIS 技术是HWANG C L 和YOON K 于1981年首次提出，其原理是最佳选择的解决方案（替代方案）与正理想解的距离应最短，而与负理想解的相距最远，换而言之，每个准则之间的距离都是根据正理想解和负理想解来计算的，这是对备选方案进行排名的准则；最好的选择是到负理想解的最大距离和到正理想解的最小距离[8]。对一个复杂系统的多个指标通过对照某些标准来判断观测结果，并赋予这种结果以一定的意义和价值过程。通过综合评价，可以有效提高管理决策的科学性，推动该专业的发展，促进人们思想观念的变化，提高理论研究水平。

TOPSIS 权重法通常包括以下5 步：准备数据，进行同趋势化处理，所有数据均需要同趋势正向化，即让所有的数据表示为数字越大越优；数据归一化处理解决量纲问题；找出最优和最劣的矩阵向量；分别计算评价对象与最优方案距离或者最劣方案距离；结合距离值计算得出接近程序值，并且进行排序比较，得出结论。

确定指标权重的方法归纳起来有主观权重法和客观权重法。主观定权法包括专家评分法、成对比较法和SAATY 权重法等方法；客观定权法有模糊定权法、熵权法、相关系数法以及秩和比法等。

2 AHP-TOPSIS综合评估模型

2.1 优选模型的建立

为了能够客观全面的对桥梁施工方案做出判断，仅仅运用传统的灰色关联决策理论是不够的，必须严格的对比考察施工评价方案和正、负理想方案之间的关联关系，从而做出合理、可靠的决策结果[9]。

2.1.1 初始评判矩阵

假设有m 个评价方案所组成的方案集S={S1,S2,…,Sm}，n 项评价指标组成的指标集合T={T1,T2,…,Tn}，方案Si对应于Tj的评判指标为xij（i=1,2,…,m；j=1,2,…,n）。则初始决策矩阵X为：

2.1.2 无量纲化处理

不同量纲的数值在灰色关联度评价中没有可比性，对决策结果影响较大，因此本文利用极差法进行量纲归一化处理，消除指标中数据量纲不同问题。通过对决策矩阵X 进行量纲归一化处理，得到标准化决策矩阵Y=(yij)m×n。

对于数值越大，指标越优型指标：

对于数值越大，指标越优型指标：

得到标准化决策模型矩阵Y，加权标准化决策矩阵Z 由标准决策化矩阵Y 与判断指数W相乘得到，如式（4）和（5）：

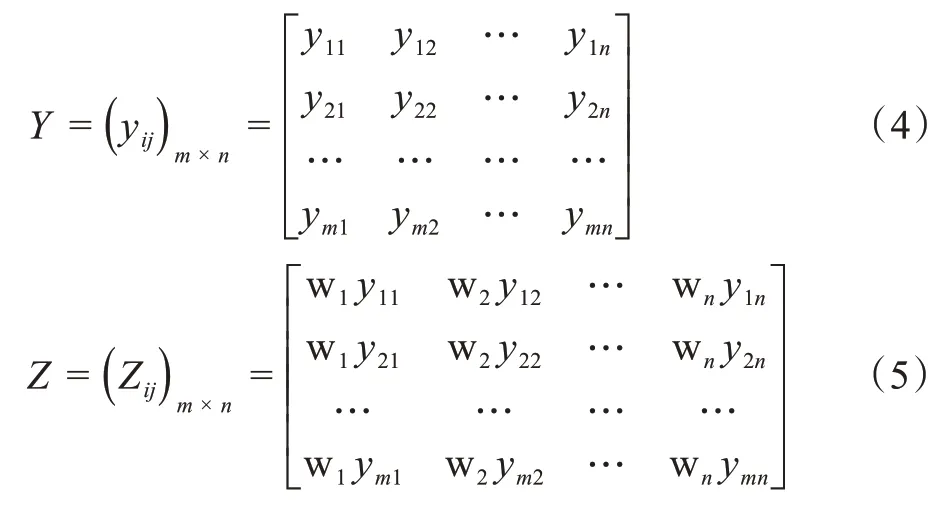
2.1.3 改进对象贴近度

根据高优指标集（越大越好）和低优（越小越好）指标集可确定评价对象的正理想解和负理想解，表示过程如下：

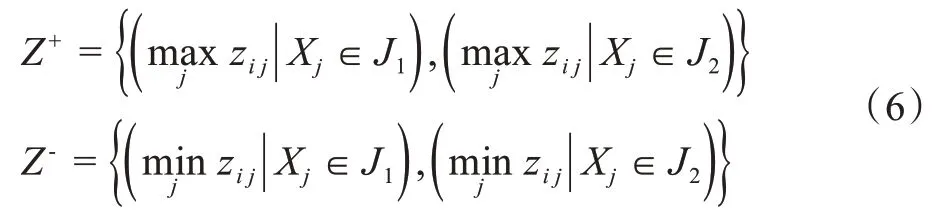
式中：Z+为正理想解；Z-为负理想解；J1为高优指标集；J2为低优指标集。

判断对象与理想解之间的距离d可能因为权重导致逆序问题[10]。故对距离d进行改进所得：

式中：d+i和d-i分别对应评判对象与正、负理想解之间的距离；Z+j和Zj分别对应Z+和Z-中的元素；wi为权重比。

最后根据d+i和d-i可求得评估对象与正理想解的贴近度E+i，过程如下：

式中：E+i为评估对象与正、负理想解的距离，直接表达出了风险对象与理想解的关系。

其中，0 ≤E+i≤1；E+i越趋近于1，说明评估对象越靠近正理想解；E+i越趋近于0，说明评估对象越靠近负理想解。因此，根据评价对象贴近度E+i的大小可对评估对象进行选择和评判，也可判断出该方案或方法是否可行。

2.2 层次分析法（AHP）

2.2.1 建立层次结构模型

在对事物中不同影响因素的重要性进行判断时，通常采用衡量和对比它们之间的某种数量的形式，从而确定各个因素的属性权重，合理的属性权重对多属性评价决策结果是否具有科学性有着直接的影响[11]。桥梁施工风险评价设计人员、环境、技术等多个层次，利用AHP法将各种混乱的评价指标进行科学分类、分层，使各个指标进行统一，对各因素进行归一化处理，最终构建出由上到下的目标层、准则层、指标层组成的评价指标体系。

2.2.2 构造判断矩阵

建立层次结构后，采用1～9及其倒数标度法，对同一指标层中的数据进行两两对比，判断其相对重要性，用1、3、5、7、9（2、4、6、8 表示之间的重要程度）αi和αj两个元素比较的程度[12]，如表1所示。

目标αi和目标αj相互比较结果用Mij表示，即Mij=目标αj和目标αi之比也可用表示。由两两元素比较而得到的相对判断指数Mij构成判断矩阵N=(Mij)：

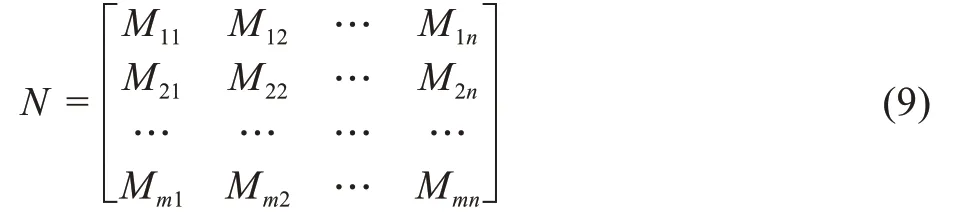
通过得到的判断矩阵N，求得该矩阵的特征根λmax和特征向量W，特征向量W 即同层次目标相对上一层次某目标重要性权重排序，通过“方根法”求得。

表1 比较标度表

表2 RI系数表

2.2.3 一致性检查

对得到的判断矩阵N进行一致性检查：

检验指标：

检验系数：

（10）、（11）式中：n 为判断矩阵阶数，RI为平均一致性指标，RI取值通过查表得到：

当CR＜0.1 时，说明判断矩阵一致性是合理的，可以接受的；当CR＞0.1时，则需要重新构造判断矩阵。

3 桥梁施工方案风险评价

3.1 施工方案评价指标体系

桥梁工程施工涉及多层次因素，本文围绕某桥梁的施工反馈意见，综合现场专家对风险指标的权衡，针对人员风险、材料设备风险、施工环境风险、其他风险4 个一级风险指标和15 个二级风险指标建立了施工方案风险评价指标体系，如表3。

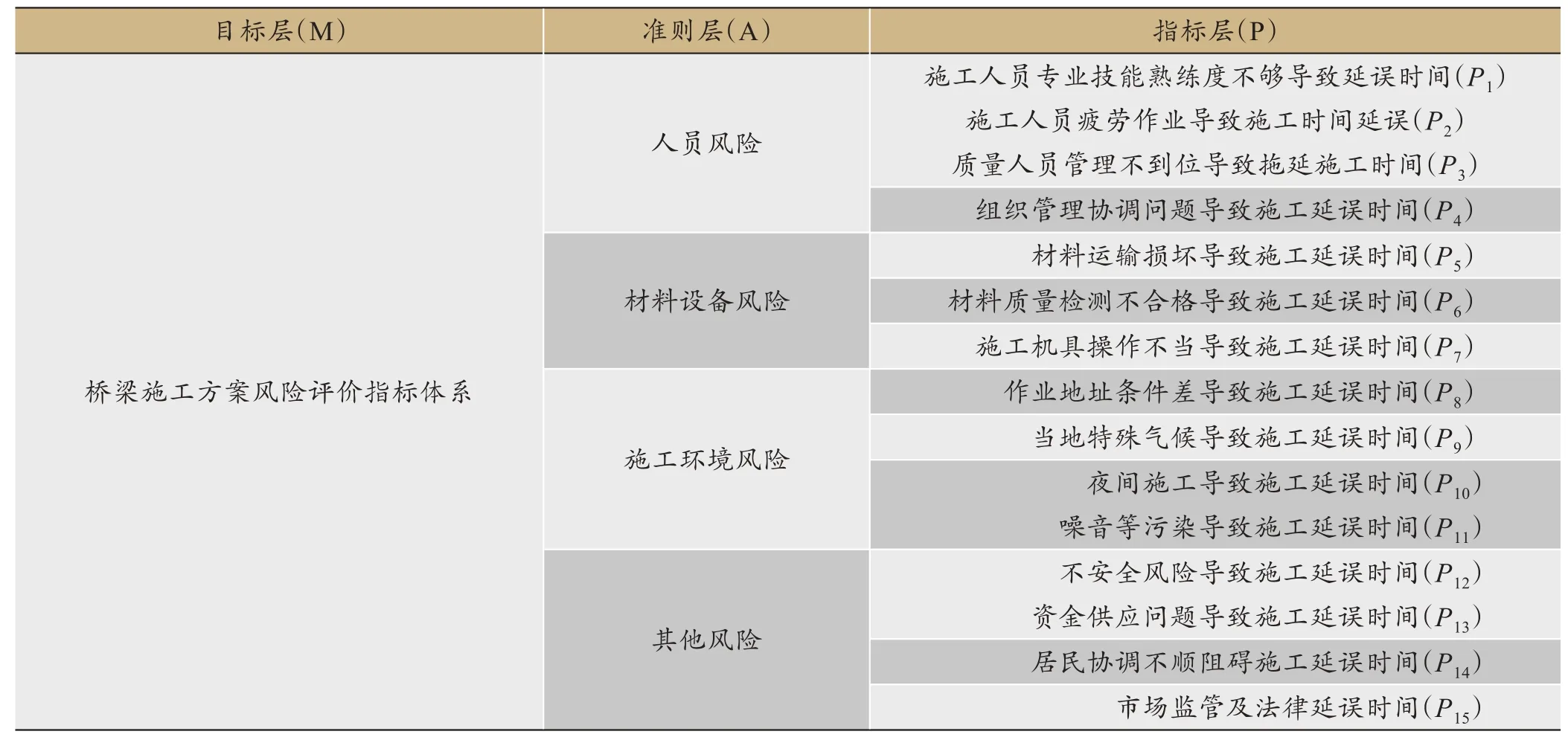
表3 桥梁工程施工方案风险评价指标体系

桥梁施工涉及到多种因素，根据AHP法原理来建立科学的评价指标体系。基于本项目有3个预设桥梁施工试验段进度方案，表4为15 个风险指标，其中由于各指标因素的影响而延误的施工时间单位为天（d）。

3.2 指标权重的确定

首先根据层次分析法构件判断矩阵，以“人员风险”为例，对本文建立的风险评价体系进行计算说明，其它风险同理。

（1）判断矩阵一致性检查

根据判断矩阵的一致性，有权重向量得到λmax=4，CI=0，查表得RI=0.89，根据公式可得到CR=0＜0.1，满足一致性检验标准，计算得到评价指标权重系数W1=[0.33,0.33,0.17,0.17]；同理，求得材料设备风险的指标权重系数W2=[0.25,0.5,0.25]。

现有评价方法有主观型和客观型评价方法[13-14]，施工环境风险和其他风险权重由现场专家经验法取得，分别征求专家个人意见（个人打分），在汇总之后按照相应的方法确定各指标权重，专家在集体会议讨论后，确定指标权重，其主观权重为：W3=[0.35,0.10,0.20,0.35]；W4=[0.385,0.195,0.290,0.130]。

（2）决策矩阵

根据公式（1）构建初始评判矩阵，得到：

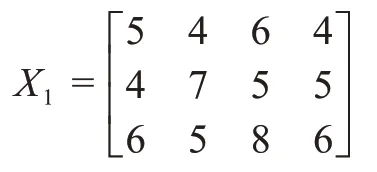
（3）无量纲化处理

根据公式（2）～（4）得到标准化决策矩阵：

由公式（5）求得人员风险的加权标准化矩阵：

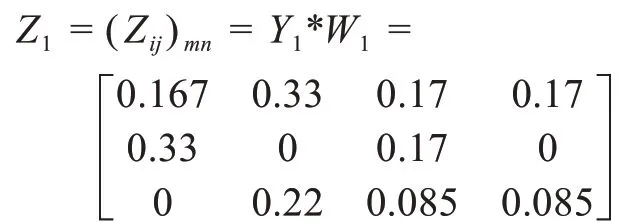
3.3 最优方案确定

根据上述方法，可以得出风险指标相对于材料设备风险、施工环境风险以及其他风险的权重值。因此，可以得出全部的加权标准决策矩阵（图1）

各种风险指标属于越小越优型指标，根据公式（8），可分别求得正、负理想解，正负、理想解的距离以及待选方案到正、负理想解的贴近度。

正、负理想解为：

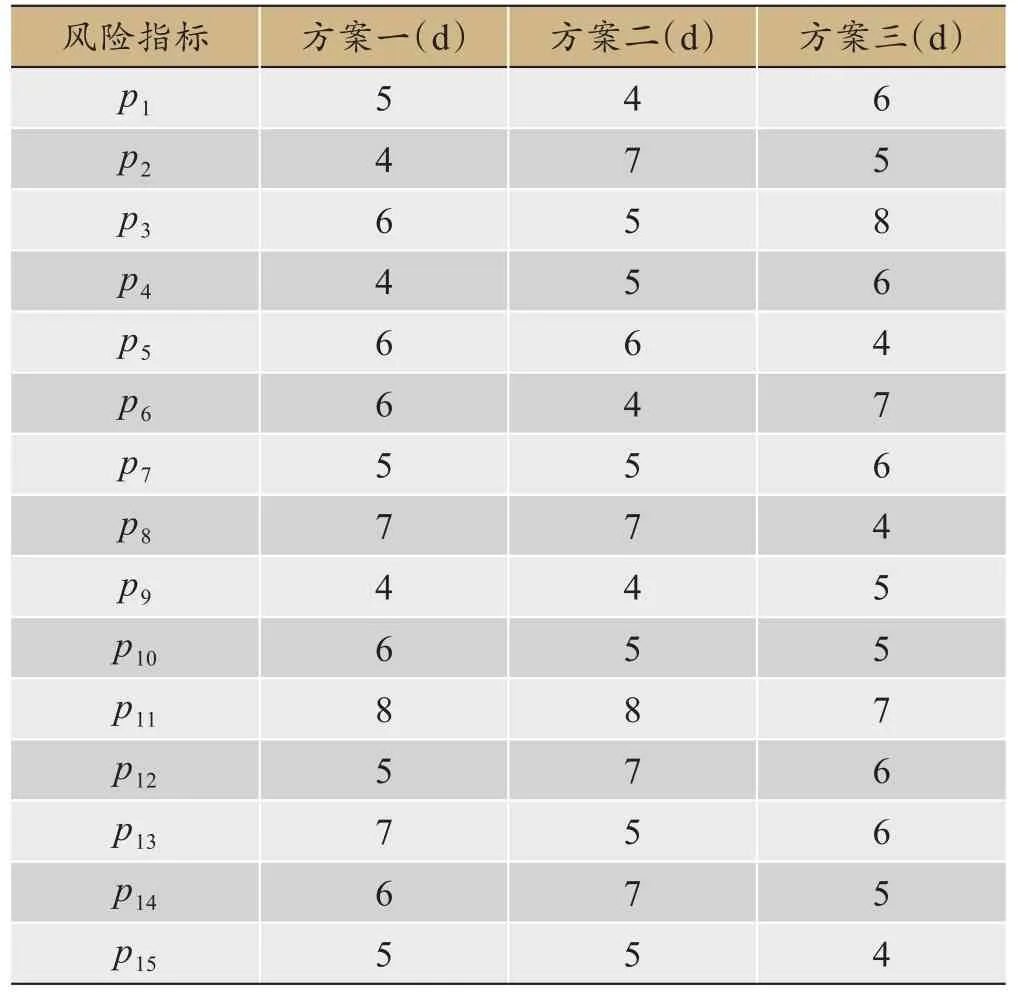
表4 各指标比选方案

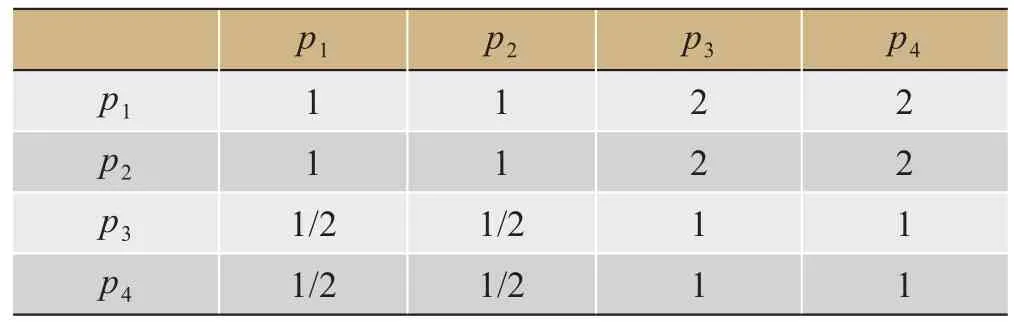
表5 判断矩阵

正负、理想解的距离：

待选方案到正、负理想解的贴近度:

综上可知，桥梁工程施工方案风险评价指标的综合优越度分别为51.8%，51.3%，47.5%。根据比较数据得知，第三种方案的风险最小，可以减少施工风险，提高施工效率。

图1 加权标准决策矩阵

4 结语

经过研究，得出以下主要结论：

（1）文章提出了改进的AHP-TOPSIS 的桥梁施工方案风险评估模型，从人员风险、材料设备风险、施工环境风险和其他风险4 个方面确定15 个具体评价指标，采用主观和客观赋权方法以避免主观片面性的影响。

（2）将模型应用到桥梁施工方案评选中，得到提出的3 个方案的优越度分别为51.8%，51.3%，47.5%，确定方案三优越于方案一和方案二，该方案更适合应用到项目中，使用该方案能够有效提高施工效率，保障施工进度和人员安全。。

（3）经工程实践的应用，证明了基于改进的AHPTOPSIS 的赋权算法在桥梁施工中时是可行的，可以有效提高工程质量，改进施工方案比选方法，为后续对桥梁风险评估研究提供理论依据与实践经验，并扩展应用到其他领域。

在后续的研究中，可继续完善研究方法。完善研究方法过于单一，主观性强，评价结果得不到最优方案，准确性不能保证，应综合使用多种评价方法选择最优方案。因存在专家主观判断和现实客观因素，凭借结果可能会受到影响，除了本文的可以层次分析法（AHP），还可引入模糊层次分析法（FAHP）；改进比选方法，将评价方法应用到其它领域或阶段。