基于稀疏贝叶斯学习的CT图像重构
何国栋,汪慧兰,章姗姗,徐建林
(1.安徽师范大学 物理与电子信息学院,安徽 芜湖 241000;2.上海市胸科医院 上海交通大学附属胸科医院,上海 200030)
0 引言
计算机断层成像(Computed Tomography,CT)自面世以来就被广泛应用到医学检查和诊断中,与X射线相比,CT影像能够提供更加全面和高分辨率的断层解剖学人体组织影像。传统的CT检查中,螺旋扫描仪旋转一周一般需要投影1 000~2 000次,较高的辐射剂量可能会对人体组织造成伤害,过量的X射线还可能造成染色体变异等不可逆转的损害[1-2]。因此,研究如何降低CT检查中X射线的投影数据量并获得清晰的医学影像,具有重要的理论研究价值和临床意义[3]。
针对低剂量采样数据的CT图像重构,一般首先对低剂量采样数据进行插值,然后再采用滤波反投影算法进行重构,还有基于迭代类的CT图像重构方法,但这些方法在实际应用中存在计算要求高、清晰度不够等问题[4]。压缩感知(Compressive Sensing,CS)是一种新兴的稀疏信号采样和处理理论[5-6],基于稀疏和随机感知理论,实现在低采样率下对稀疏信号的高效精确重构,目前CS已经被广泛应用于模拟信号到信息转换[7]、卫星导航信号处理[8]以及无线传感器网络[9]等领域。由于CS能够以较少的采样数据实现对稀疏信号的高质量重构,将其应用到低剂量肺部CT图像重构中,临床应用上可以降低医学检查中X射线对人体的二次伤害。CS的重构算法较多,稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)重构算法是一种性能较好的重构算法[10]。SBL最初作为一种机器学习算法,后被引入压缩感知稀疏信号重构中,研究发现该算法能够有效地重构出稀疏度较低的信号,有利于实现对图像信号的重构。
本文对压缩感知理论和 SBL算法的原理进行详细介绍,并建立了基于小波函数的肺部CT图像稀疏表示。对低剂量随机采样的肺部CT图像数据,应用SBL算法进行重构,仿真结果显示,所提方法能够有效地重构出清晰的肺部医学影像。
1 基本理论
Nyquist采样定理要求信号的采样频率须达到信号最高频率的两倍以上,对高频信号的系统要求较高,且产生大量的冗余数据。CS理论提出,可以对稀疏信号以较低的采样率进行采样,并通过重构算法精确重构出原信号[11]。基于CS理论,如果信号x∈RN×1在某个变换基Ψ下可以稀疏表示为:x=Ψs,其中信号s∈RN×1中大部分元素数值为0,则信号x称为稀疏信号。对稀疏信号应用随机矩阵Φ∈RM×N(M≪N)进行测量:
y=Φx+ω=ΦΨs+ω=Θs+ω,
(1)
即可得到较少的观测数据y∈RM×1,其中ω为噪声。从测量结果中恢复出原信号,即CS信号重构。在式(1)中,方程的个数远少于未知数的个数,这是一个欠定数学问题,理论上原方程的解有无数种。如果加上稀疏约束,当方程的个数满足一定要求,即可得到正确的稀疏解,能够精确恢复出原稀疏信号[12-13]。用0范数表示求信号中的稀疏个数,则CS信号稀疏重构问题可表示为:
s= argmin||s||0s.t.y=Θs,
(2)
式中,求解的是一个NP-hard问题,需要通过组合优化的方法才能找到最优解,当N很大时,找到稀疏最优解非常困难。
稀疏贝叶斯学习是机器学习中一种重要的学习算法,在贝叶斯理论基础上发展起来,由 Tipping等人在2001年前后提出,后被引入到压缩感知稀疏信号重构中[14-15]。在式(1)中假设ω是均值为0、方差为σ2IM的高斯分布,则可得到y符合均值为Φx,方差为σ2IM的高斯分布,即:
(3)
假定x的每个元素都服从一个参数化的均值为0方差为γi的高斯分布,则有:
(4)
式中,Γ=diag(γi),γi是未知的参数,由算法自动估计计算。算法迭代中,大部分γi会趋于0,SBL通常采用一个阈值将趋于0的γi置为0,阈值大小由实际数据和噪声决定。当γi=0时,相对应的xi也为0,因此得到稀疏解。应用贝叶斯公式和全概率公式可得:
(5)
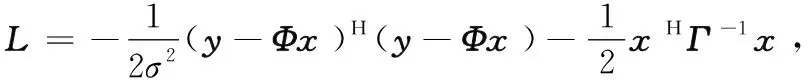
(6)
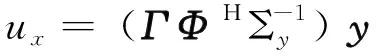
(7)
(8)
已证明基于SBL的稀疏信号重构能获得全局最优解,且在感知矩阵列之间相关性较高时,SBL也能够获得较好的重构效果,目前SBL在稀疏度较低的信号重构中应用较多。
2 CT图像的稀疏表示
CT图像如图1(a)所示,由于肺实质和空气对射线的吸收率低,胸腔内大部分区域显示的均为黑色,而其余组织如肺结节、骨骼及脂肪等对射线的吸收率较高,在CT影像中显示为白色。肺部CT图像是非稀疏的,压缩感知应用的前提是信号必须是稀疏的,因此首先需要考虑图像的稀疏表达[16]。多分辨率分析是一种常用的图像稀疏分析工具,对图像进行小波变换后,可以得到稀疏的表达效果,应用较多的有小波变换、Contourlet变换等[17]。应用Haar小波函数对肺部图像进行一次变换,变换的低频和高频信息如图1(b)所示,图像的低频部分(左上)保留了图像的大部分信息,而高频部分大部分数据为0,在图像中显示为黑色的部分,即整个胸部影像在Haar小波基下是一种稀疏信号,图像可以稀疏表示为:
I=ΨS,
(9)
式中,I表示图像信号,Ψ表示小波基,S表示稀疏信号。
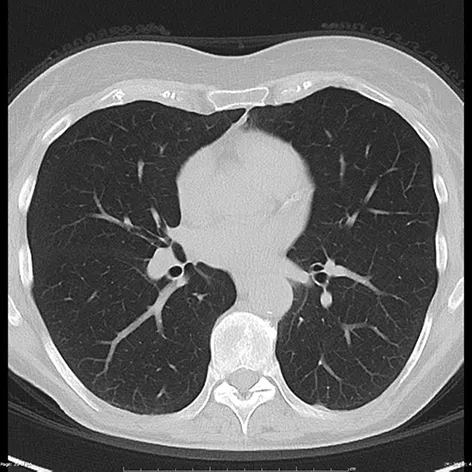
(a) CT图像
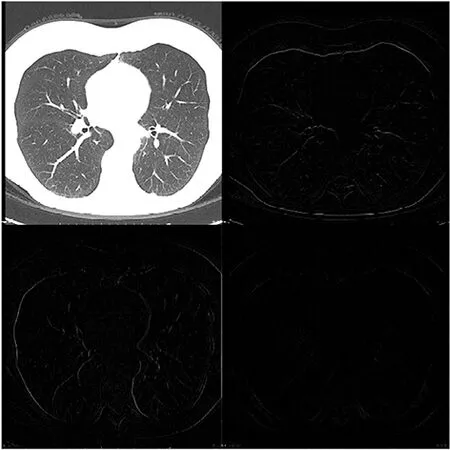
(b) 基于小波基的CT图像稀疏表示
3 仿真实验
为了验证本文提出的低剂量随机采样的肺部CT图像重构方法的可行性和有效性,应用Matlab软件对其进行仿真,其中随机测量矩阵使用归一化的零均值高斯分布随机矩阵。实验图像选自上海市胸科医院,首先应用随机测量矩阵对肺部CT图像进行感知,获得低剂量的随机采样数据,然后构造基于Haar小波函数的稀疏基,最后应用重构算法对肺部图像进行重构。为分析对比重构效果,使用图像峰值信噪比(Peak Signal to Noise Ratio,PSNR)作为评价重构效果的客观评价标准,其计算公式为:
(10)
式中,MSE为原图像和重构图像的均方误差,n为图像的灰度级。为分析问题方便,定义压缩率(Compression Ratio,CR)为:
(11)
式中,M为低剂量投影后的数据量,N为原始数据量。
实验一设置为在相同压缩率下应用不同重构算法的重构实验,选择压缩感知常用的3种重构算法:正交匹配跟踪(Orthogonal Matching Pursuit,OMP)、L1范数和SBL重构算法进行实验,图2 为压缩率为0.5时的重构结果。对比3种重构算法的重构结果,主观评价OMP算法效果不够理想,L1范数重构和SBL重构效果较好,PSNR值分别为31.245 2和32.081 2。

(a) 原图
实验二设置为当压缩率分别为0.2、0.4和0.6时,只应用SBL算法的重构实验,实验结果如图3所示。当压缩率为0.2时,由于投影数据量太少,重构效果较差,重构的肺部影像中有大量的伪影。当压缩率为0.6时重构效果较好,主观评价和原图差别不是很大,PSNR值达到了34.180 9,基本能满足医学检查要求。从两组实验可以看出,压缩率太低则所能提供的信息太少,重构的肺部图像不能满足临床应用的需求,但在同一压缩率下,SBL算法重构效果较好。

(a) 原图
实验三分析在不同压缩率(0.2~0.8)下不同算法的重构效果,对同一肺部图像应用3种重构算法分别进行100次实验,取100次实验的PSNR平均值,实验结果如图4所示。
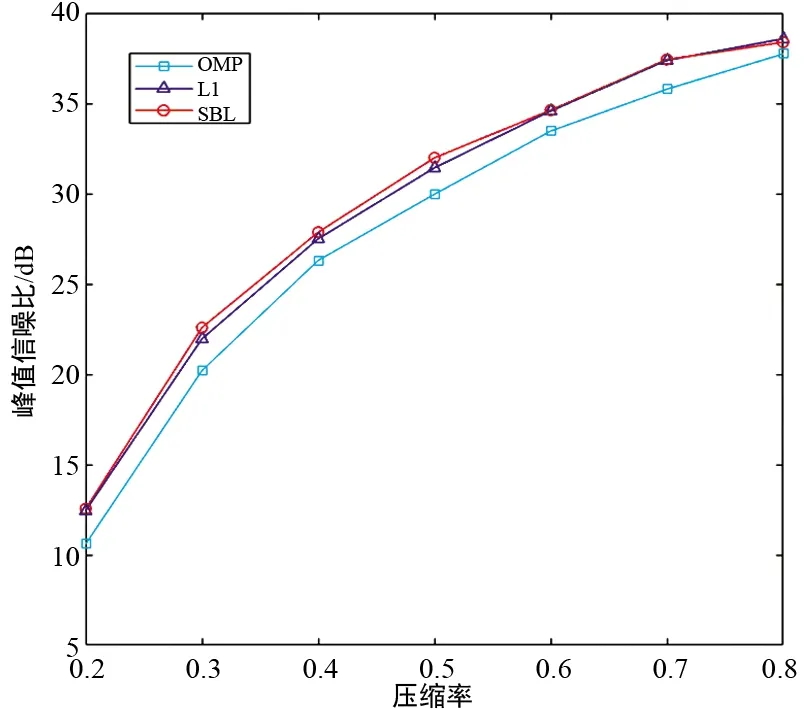
图4 不同压缩率下重构结果Fig.4 Reconstruction results with differentCR
在同一压缩率下,OMP算法重构的PSNR值低于其他2种算法,L1算法和SBL算法重构的PSNR值比较接近。PSNR值随着压缩率的增大而增大,因为随机采样的数据越多,提供的重构信息就越多,重构效果就越好。当然,CT检查的辐射量也随之增大。
4 结论
压缩感知是一种新颖的信号采样处理理论,能够在低采样率下有效地重构出原稀疏信号。将该理论应用到医学CT检查中,利用高斯随机分布的压缩矩阵对肺部图像进行压缩采样,应用小波函数实现对CT图像的稀疏表达,最后应用稀疏贝叶斯学习算法对肺部图像进行重构。大量的仿真结果显示,该方法有效可行,当压缩率为0.6的时候,重构的肺部组织图像清晰,PSNR值满足医学检查需求。将压缩感知应用到医学CT检查中,实现了在低剂量采样下对医学图像的重构。该方法能够减少医学检查中的辐射剂量,从而降低辐射对人体造成的伤害,具有重要的研究意义和临床应用价值。

