分汊河道近底水流特性试验研究

张 婕, 王平义*, 胡杰龙, 王梅力

(1.重庆交通大学， 水利水运工程教育部重点实验室， 重庆 400074； 2.重庆交通大学国家内河航道整治工程技术研究中心， 重庆 400074; 3.重庆交通大学建筑与城市规划学院， 重庆 400074)

水力特性特别是流速特性对分汊型河道的泥沙起动、滩槽冲淤、分流分沙比、整治建筑物局部冲刷等均有较大影响，其中近底水流起直接作用。分汊河道作为一种重要的河流形态,在长江中游广泛存在，水流特性是研究分汊河道河床演变、整治工程等的重点。王云飞[1]、许海勇[2]、肖庆华等[3]相继开展了二维水沙数值模拟，得到长江中下游分汊河道水流运动特性等研究成果，其中不同流量下不同区域内断面平均流速分布特征以及变化规律是研究的重点。刘晶等[4]、常宏兴等[5]利用三维数学模型，探讨分析了分汊河段水流结构的三维特性，结果表明表层和底层流场存在较大的差异，主要体现在水流弯曲曲率以及分流宽度上。物理模型试验也是研究分汊河道水流特性的重要手段，李仟等[6]、顾莉等[7-8]、邹骥等[9]对长江中下游不同河段开展了相应的试验研究，分析了不同洲滩形态、来流量、汊道宽度比等因素下的水流结构特性及紊动强度，研究成果主要包括断面平均流速以及紊动能分布规律，弯曲分汊河道流场存在明显的环流特征，环流强度主要受江心洲位置的影响。上述的研究采取不同的研究方法，对长江中下游分汊河段水流特性与紊流结构进行了较为充分的研究，但在分析流速分布等问题时均以垂线平均流速为研究对象，没有考虑近底流速分布规律及其对洲滩冲淤的影响。

近年来，采样测量分析等技术飞速发展，越来越多的研究者将目光聚焦近底水流结构，通过模型试验、理论分析、数值模拟等手段，对泥沙起动[10-13]、河床变形[14-17]、局部冲刷[18-19]等问题进行了研究。袁俊[16]通过多组水槽试验，利用数理统计、平稳随机过程理论等方法对近底流速进行了统计分析，发现近底流速属于低频域信号，其振幅符合正态分布，圆频率及相位角符合均匀分布。赵亚飞等[20]通过对比矩形水槽横向测点的流速结构差异，分析了近底流速分布的变化特点与近壁两侧的流速结构变异，结果显示近底流速的相对脉动强度呈现中间区域最大并向两侧递减的趋势，在临近侧壁处有突变波动现象。袁俊[16]、赵亚飞等[20]的研究模拟的河道断面多为矩形，在近底水流流速分布、紊动结构等问题上取得了较大的进展。然而天然河道断面并不是规则的矩形，特别是洲滩的存在，使得实际断面的水流特性与矩形断面水流特性存在较大的差异。弄清天然分汊河道近底水流特性对研究洲滩冲淤、整治建筑物稳定性起着重要的作用。基于此，在收集长江中游洲滩原型资料的基础上，通过建立物理概化模型试验，探究近底流速分布规律以及近底水流脉动特性。

1 概化试验

1.1 试验设计

长江中下游存在大量的分汊河道，而其中大部分按照钱宁[21]和余文涛[22]的分类方法和标准可将其定义为顺直分汊河道。夏禹[23]对长江中下游顺直分汊河道形态尺寸进行了归纳。本次试验在夏禹收集的顺直分汊河道武汉天兴洲段原型资料的基础上设计了概化模型，表1为尺寸参数。

表1 概化模型尺寸

几何比尺和流速比尺公式为

(1)

式(1)中：λL为长度比尺；λH为水深比尺；λV为流速比尺。

三峡水库建成后长江中下游径流过程发生了较大的变化，在前期工作中，收集了武汉水文站2003—2015年的日径流资料，利用数理统计方法和随机理论对武汉站日径流序列进行了随机模拟[24]。本次试验考虑极大洪峰下的径流过程，对其进行台阶化处理,流量过程如图1所示。模型试验在重庆交通大学河海学院试验基地进行，试验水槽长 30 m，宽3 m，模型河底坡降取0.1‰。试验段共布置13个横向断面，每个断面上设置14个测点(由右壁至左依次标记为H1～H14)，相邻测点间相距 20 cm，概化模型及测点布置如图2所示。

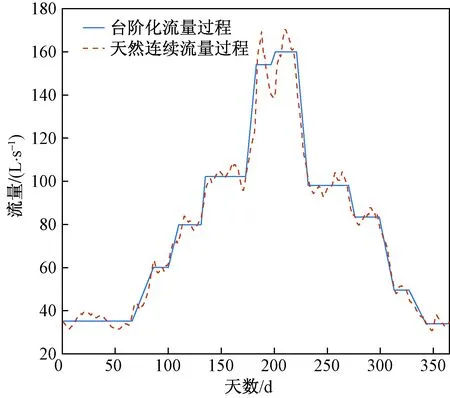
图1 日径流模拟序列Fig.1 Daily runoff simulation series

采用长时跟踪法，采集全流量过程流速及水位数据。模型试验水槽进口流量由矩形薄壁堰控制，尾门由翻板门结合小水阀控制。流速测点布置在离底面1 cm的深度，采用重庆交通大学自行研制的旋浆流速(谱)采集系统进行测量。该系统由软件、数据采集卡、传感器、放大器、旋浆等构件组成。流速数据采集系统为瞬变流速长时跟踪采集系统，由重庆交通大学河海学院自行研制，采样频率设定为3 000次/s。水位测量采用同步自动测量系统，由西南水运科学研究所研发，采样频率为1次/s，系统利用超声测距原理，结合先进的传感技术和电子技术，同步采集、记录不同测点的水位数据。

W1～W13为横向断面图2 概化模型及测点布置Fig.2 Generalized model and layout of measuring points

1.2 试验数据预处理

在流速信号的采集、量化、传输过程中，由于测量环境、人为因素、元件系统等噪声的干扰，使测量数据或多或少地受到污染。在分析研究前，应当对采集到的数据进行预处理以尽可能地消除噪声。常见的方法有3σ准则法、多项式逼近法、小波去噪法等。采用3σ准则法对采集到的数据进行预处理。

2 结果分析

任一方向的瞬时流速可以表示为

(2)

表2 分级流量

2.1 近底水流时均流速分布特性

近底水流受紊流涡团的强烈影响，床面附近水流运动十分复杂。测试断面不同流量近底时均流速沿横向分布如图3所示。

图3(a)为分流区近底时均流速沿横向分布，其中断面W1距离滩头150 cm，断面W2距离滩头 50 cm，断面W3为滩头与槽底相接处。从图3(a)中可以看到，离滩头较远的断面近底时均流速沿横向分布比较均匀，近底水流受滩体分流作用影响较小。断面W3位于滩头与平底交界处，受江心洲分流作用影响大，河槽中部流速减小，两条支流(左右汊)流速增加明显，流向分别偏向左右两侧，形成中间小两边大的流速分布规律。分布选取位于逆坡段、滩顶段以及顺坡段3个断面，对其近底时均流速分布进行分析，如图3(b)所示。从图3(b)中可以看出，顺坡段位于江心洲下半段，沿主流方向滩面高程逐渐降低，流速分布表现为中间低两边高的特点；滩顶段高程不变，来流量较小或一般时，除滩槽交界处的个别点存在突变外，近底时均流速大小沿横向基本一致；当来流量比较大时，流速在横向分布上的波动性增强，但总体上仍保持在一个较窄的区间内。逆坡段位于江心洲的上半段，沿主流方向滩面逐渐抬高，在大流量下，近底时均流速沿横向表现为中间略高的特点，与顺坡段流速的分布有明显的差异，其他流量条件下流速沿横向呈较为均匀的分布。

图3 不同流量下近底时均流速横向分布Fig.3 Transverse distribution of time-averaged velocities under different flows

图4 近底时均流速沿纵向分布Fig.4 Longitudinal distribution of time-averaged velocities

而沿水流方向，滩面高程呈先增大再不变后减小的变化过程，近底时均流速沿纵向分布如图4所示。对于滩面范围内的断面而言，由于滩体高程的逐渐抬高，近底时均流速随之增大；到达滩顶段后，流速虽有波动但总体变化不大；在滩体下半段，高程逐渐降低，流速迅速下降。对于左右汊而言，沿水流方向底部高程基本保持不变，近底时均流速变化相对较小，但受汊道进口断面收缩以及出口断面放大的影响，进出口的流速出现了一定幅度的起落。

2.2 近底时均流速随水深变化规律

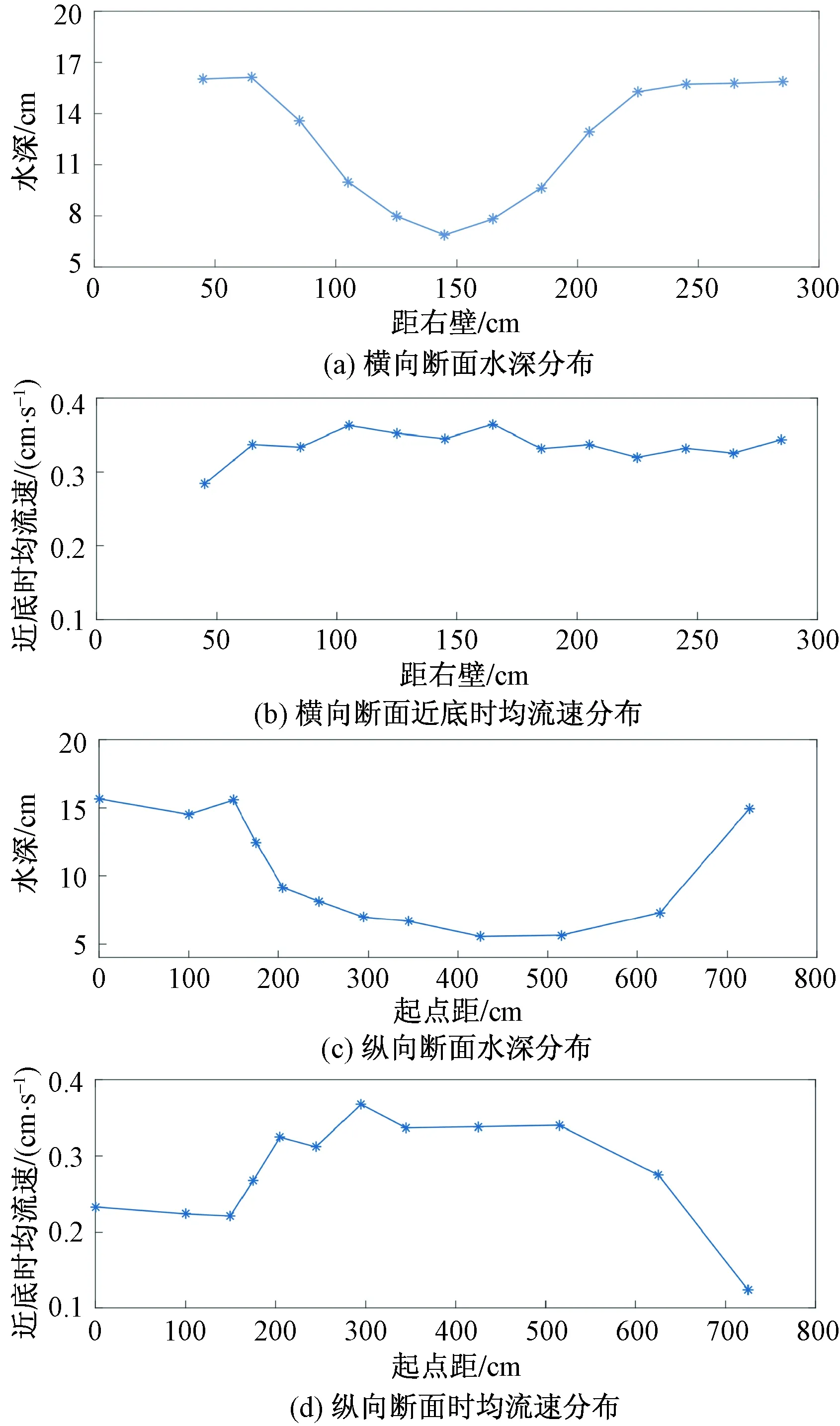
图5 流速随水深变化曲线Fig.5 Flow velocity curve with water depth

从时均流速在横向与纵向上的分布可以看到，近底流速受地形的影响较大。特别是在江心洲范围内，地形起伏较大，测点以上至水面的水深随之变化，进而影响近底时均流速。选取流量150 L/s下的横断面W7以及纵断面H6，分别研究近底时均流速与水深的关系，如图5所示。从图5中可以看到，近底时均流速与水深是呈负相关的。受地形起伏的影响，流速测点以上至水面的水深变化较大，在横向上深槽内水深最大，经滩槽交界区至滩面水深逐渐减小，滩顶处水深最浅。在纵向上水流依次经过底部逐渐抬高的逆坡段、滩顶段，以及底部逐渐降低的顺坡段。试验中近底流速这种异于平底河床流速的分布特性正是由于河床面坡度变化造成的。当水流由河床低处向高处流动时,表现为单宽过水面积的逐渐减少,使水流受到来自河床面的收缩挤压而产生的束狭作用,并促使中、底层水流流速急剧增大。王伟[25]指出，这种来自河床面坡度变化所产生的束狭作用是由河底向上逐渐减少的，从而导致流速的增大也是自下而上递减的，即束狭作用对底层流速影响最大。

2.3 近底水流脉动特性

2.3.1 近底水流脉动强度随来流量变化特性

图6 近底水流相对脉动强度变化曲线Fig.6 Variation curve of relative fluctuation intensity

2.3.2 近底水流脉动强度分布

分析可知，洲滩高程起伏对近底流速影响较大。为了解滩槽不同位置处近底水流紊动强度，对实测流速数据进行整理，得到不同流量下近底各测点处的相对脉动强度，其沿不同横断面分布如图7所示。

分流区测点断面W1沿横向各测点高程相同，且距离滩头位置较远，近底水流相对脉动强度除在个别测点有所波动外，整体沿横向分布较为均匀。进入汊道段后，江心洲的存在使得地形起伏较大，断面W7位于江心洲上部，滩面区(距右壁104～184 cm范围内)水深小而流速大，深槽区(距右壁24～64 cm及224～264 cm范围内)水深大而流速小，因此滩面及深槽区近底水流的相对脉动强度相对较小，唯有在滩槽交界处(距右壁84 cm及 204 cm)水流流体复杂，紊动增强，相对脉动强度出现明显的突变。测点断面W9位于滩顶区域内，小流量下滩面范围的水深极浅，导致水流紊动强烈，而在深槽区水深相对较大，水流也较为平稳，在大流量下由于整体相对脉动强度均不大，因此这种变化特征表现地并不明显。

图7 不同流量下近底水流相对脉动强度分布Fig.7 Distribution of relative pulsation intensity under different flows

2.3.3 近底水流脉动能

图8 汊道段近底脉动能变化曲线Fig.8 Bottom pulsation energy variation curve

近底水流属于紊流，由无数大小不一的涡流组成，具有较强的动能，对泥沙运动以及床面变形起着重要的作用。长江干线12月至翌年3月为枯水期，流量较小，自4月份开始来流量上涨，水位逐渐抬高，6—9月一般为洪水期，流量达到最大。10月份之后，流量逐渐减小，水位回落。图8显示了涨水过程中近底水流脉动能随流量变化特性。分流区地形平整，水流较为平稳。枯水期来流量小，流速缓慢，近底水流的脉动能不大，虽然随着流量的增长脉动能有所上涨，但增幅较小。自进入中水期开始，随着来流量逐渐增加，近底水流脉动能显著增大，到洪水期脉动能达到最大。汊道段近底水流脉动能整体上同样呈上涨趋势，不同于分流区的是在枯水期近底水流脉动能上涨幅度更大，这是江心洲对河道束窄作用导致的。江心洲的存在使得河道宽度减小，即使在枯水期，流量上涨引起的流速变化更为剧烈，水流脉动能也随之快速增强。从整个涨水过程来看，洪水期近底水流脉动能最大，中水期次之，枯水期最小。

3 结论

(1)由于江心洲的存在，分汊河道河床高程起伏明显，这对近底水流流速有较大的影响，具体表现为河床面高的地方水深较浅，水流受河床压缩作用导致流速增大，这一特征在汊道区近底水流时均流速沿横向纵向的分布上均有所体现。分流区河床平整，离滩头较远处的测点断面流速沿横向分布均匀；而在滩头与平底河床交接处的近底时均流速受水流分流作用明显，沿横向呈两边大中间小的分布规律。

(2)相对脉动强度一定程度上可以反映近底水流的紊动强弱。随着来流量的增大，不同区域内的近底水流脉动强度变化规律并不相同。在分流区内，随着流量的增大近底水流相对脉动强度急剧减小，其中枯水期涨水以及行洪过程中相对脉动强度变化幅度较大，而在中水期相对脉动强度的变化则较为缓慢。在汊道区内，枯、中水期近底水流的相对脉动强度虽有波动但幅度较小，在洪水流量下相对脉动强度大幅下降，明显小于中小流量。

(3)受近底时均流速与水深的影响，不同区域内的相对脉动强度沿横向分布也不尽相同。具体表现为：分流区分布均匀，汊道区逆坡段滩槽交界处水流脉动较其他位置大；汊道区滩顶段滩面处水流脉动最强。

(4) 近底水流的脉动能对泥沙运动以及床面变形起着重要的作用。在整个试验测量区域内，近底水流的脉动能均随来流量的增大而增大，不同的是在枯水期分流区内测点的脉动能增长速度较慢，而汊道区内测点的脉动能增长速度明显更快。

此外，本次试验没有考虑主支汊宽度比的变化对近底水流的影响，而事实上江心洲位置时常左右摆动，后续将进行更加深入的研究。