一种考虑迟滞的动力电池模型及其参数识别*
王琨,徐鹏,李呈旭
一种考虑迟滞的动力电池模型及其参数识别*
王琨1,徐鹏1,李呈旭2
(1.盐城工业职业技术学院汽车与交通学院,江苏 盐城 224005; 2.江苏大学汽车与交通工程学院,江苏 镇江 212013)
建立精确的电池模型是实现电池管理策略仿真及验证的前提,是实现对动力电池进行全面、高效、精细化的管理的关键。然而在动力电池充放电过程中出现的电压迟滞现象,严重影响了动力电池的建模精度。文章建立了一种考虑锂离子电池充放电电压迟滞的电池模型,并对其进行了参数识别,可供从事相关锂离子电池状态分析的研究人员作为参考。
电池管理;充放电迟滞;建模
前言
近些年来动力电池电芯技术实现了较快的发展,给电动汽车的动力存储提供了很多新的选择,但是仅仅依靠单体技术和材料的进步不能保证电动汽车使用安全性、可靠性以及电动汽车中电池的成本效率,对动力电池进行全面、高效、精细化的管理是最终满足实际车用需求的重要环节。建立精确的电池模型是实现电池管理策略仿真及验证的前提。然而动力电池在充放电过程中通常会出现充放电曲线不重合的情况,这种动力电池的固有特性对其建模精度产生了重要的影响。
动力电池等效电路模型通过传统电阻、电容、理想电压源等物理元件组成电路来模拟动力电池的外特性。其中电压源表示电池的热力学平衡电势,RC网络描述电池的动力特性。等效电路模型对动力电池的充放电特性有良好的适应性,而且容易推导出模型的状态方程,被研究者们广泛地运用于电动汽车建模仿真和基于模型的BMS开发[1-2]。
常见的等效电路模型有 Rint模型、RC模型、Thevein模型以及在上述模型基础上改进得到的PNGV和GNL模型。如图1所示,Rint模型结构比较简单,没有考虑动力电池的极化效应和内阻变化,误差较大;Thevenin模型在Rint模型基础上增加了一对电阻和电容用来反映电池极化效应和内阻变化,但不能反映电池充放电过程中开路电压随电池SOC值的变化[3];PNGV模型在Thevenin模型基础上增加了一个电容,解决了开路电压随电池SOC值变化的问题,但模型较复杂,运算成本高。RC模型由2个电容和3个电阻构成,其中大电容C表示电池的可用容量,小电容C表示电池的表面效应,R、R、R分别表示极化电阻、表面效应电阻和终端电阻,能够较好地反应电池的SOC和内阻特性[4]。
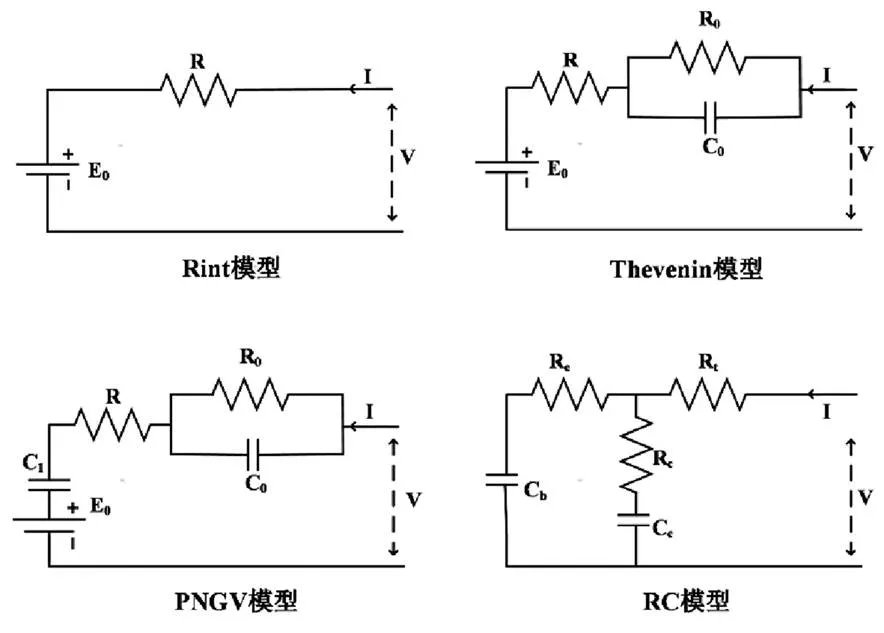
图1 常见等效电路模型
2 改进型电池模型的建立
本文考虑动力电池在充放电过程中存在较大的充放电电压迟滞,结合典型的动力电池等效电路模型的特点,在RC等效电路模型的基础上,建立了带迟滞的改进型RC电池模型。将迟滞电压U加在RC等效电路模型的终端,建立的改进型RC等效电路模型,如图2所示。电容C表示电池的表面效应,R、R、R分别表示极化电阻、表面效应电阻和终端电阻,V代表开路电压,U表示电池充放电迟滞电压的数值。
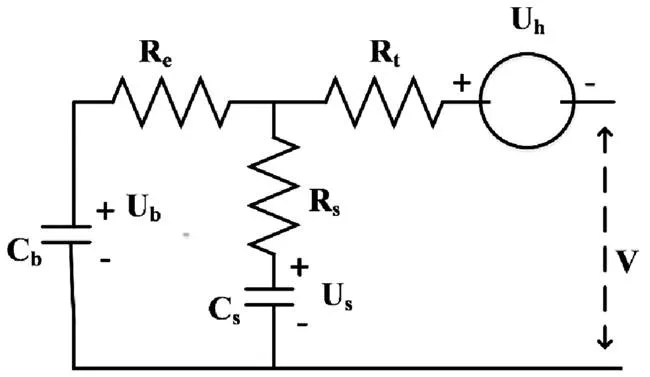
图2 带迟滞的改进型RC等效电路模型
根据电路原理对该电路模型进行数学推导得到改进型RC等效电路模型数学方程如下:


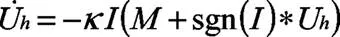
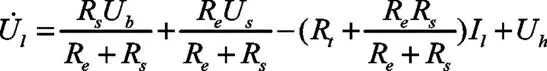
式中:U为电容C两端的电压;U为电容C两端的电压;U为电池的迟滞电压;U为负载电压;I为负载电流。
3 模型参数辨识
本文应用混合脉冲功率性能测试(HPPC)实验对RC电路模型中的参数进行辨识。利用最小二乘法指数拟合电池的端电压对电流的响应曲线,进而求出RC模型中的电路参数。试验方法如下:选取一个SOC点,测试前先将电池都静置1小时,然后对电池进行20s的恒流放电,停止40s后再进行20s的恒流充电,图3是电池放电后静置阶段截取的电压曲线。
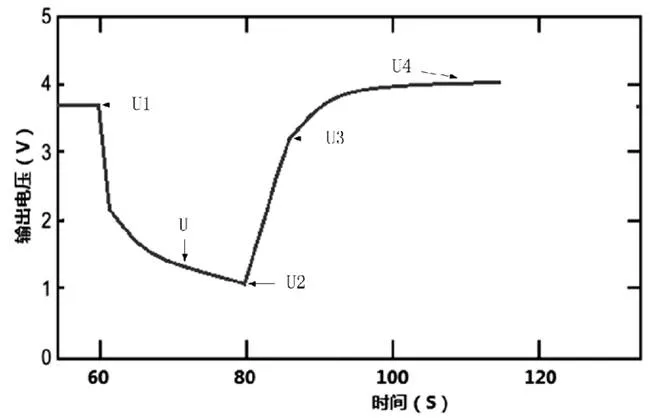
图3 恒流放电电压曲线
在参数拟合过程中,电池输出的电压值已经去除了迟滞电压U,根据图3中的电压曲线求取模型的参数如表1所示:
表1 改进型RC模型参数
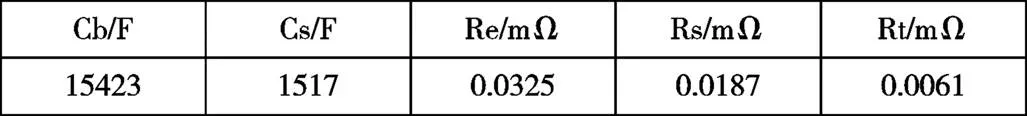
4 结语
随着新能源汽车行业的快速发展,电动汽车动力电池管理系统(BMS)得到了相关工业界和学术界的广泛关注和研究。作为电池管理系统设计的核心,能够对动力电池实施精确建模是关键,也是近年来学术界和工业界研究的热点。本文对常用的动力电池等效电路模型进行了简要分析,在RC等效电路模型的基础上建立了带迟滞的改进型RC电池模型,并利用HPPC实验对RC电路模型中的参数进行了辨识。通过最小二乘法指数拟合端电压与电流的关系曲线,进而求出了RC模型中的电路参数,是进一步对动力电池进行管理策略仿真及验证的重要基础。
[1] Thele M,Bohlen O,Sauer D U,et al. Development of a voltage- behavior model for NiMH batteries using an impedance-based modeling concept[J]. Journal of Power Sources, 2008, 175(1): 635- 643.
[2] Wang S,Verbrugge M, Wang J S, et al. Multi-parameter battery state estimator based on the adaptive and direct solution of the governing differential equations[J].Journal of Power Sources,2011,196(20): 8735-8741.
[3] 张树梅.基于磷酸铁锂单体电池荷电状态的均衡算法研究[D].上海:上海交通大学,2015.
[4] 张吉星.纯电动汽车动力锂离子电池SOC估计算法研究[D].长春:吉林大学,2015.
Power Battery Model with Hysteresis and Its Parameter Identification*
Wang Kun1, Xu Peng1, Li Chengxu2
(1.School of Automotive Engineering, Yancheng Vocational Instition of Industry Technology, Jiangsu Yancheng 224005; 2.Automotive Engineering Research Institute, Jiangsu University, Jiangsu Zhenjiang 212013)
The establishment of an accurate battery model is a prerequisite for the simulation and verification of battery management strategies, and is the key to a comprehensive, efficient and refined management of power batteries. However, the voltage hysteresis in the charging and discharging process of the power battery seriously affects the modeling accuracy of the power battery. In this paper, a battery model considering the hysteresis of lithium-ion battery charging and discharging voltage is established, and its parameters are identified, which can be used as a reference for scholars engaged in the analysis of related lithium-ion battery status.
Battery management; Charge and discharge hysteresis; Modeling
10.16638/j.cnki.1671-7988.2021.07.001
U469.72
A
1671-7988(2021)07-01-03
U469.72
A
1671-7988(2021)07-01-03
王琨,就职于盐城工业职业技术学院汽车与交通学院,工学硕士,从事电动汽车动力电池研究。
盐城市科协软课题《长三角一体化背景下盐城市新能源汽车动力电池产业发展路径研究》(编号yckxrkt2020-9)资助。

