基于子结构模型的室内火灾下钢框架结构倒塌分析

任 文 赵金城

(上海交通大学船舶海洋与建筑工程学院， 上海 200240)

火灾中，钢框架结构的倒塌时间对消防救援具有重要意义.同时，火灾下结构倒塌也是性能化防火设计的重要标准之一[1].因此，火灾下钢框架结构的抗倒塌性能和倒塌时间都具有重要的研究意义.

目前，火灾下钢框架结构倒塌研究主要以试验研究[2]和有限元分析[3]为主.倒塌研究内容以钢框架结构火灾下的倒塌机制为主，结构倒塌时间以及不确定性研究还较少.结构倒塌易损性分析方法是一种可以考虑随机变量不确定性的分析方法.然而，易损性分析方法往往需要计算大量模型，采用整体结构模型进行分析会耗费大量时间.同时，建筑物防火设计中往往会设置防火分区，结构发生的火灾常为室内火灾或者局部火灾.根据室内火灾下钢框架结构的相关研究[4]，室内火灾对结构的影响范围是有限的.因此，采用子结构模型进行火灾下结构倒塌易损性分析，可以节省计算时间、提高分析效率.

本文基于子结构模型提出了一种火灾下钢框架结构抗倒塌性能简化评估方法，该方法以结构倒塌时间的可靠指标作为结构抗倒塌性能的定量评估标准.首先，根据室内火灾下结构的倒塌模式确定了钢框架子结构模型的选取范围，并通过矩阵分析方法推导出子结构模型的边界条件；其次，基于易损性方法提出了室内火灾下钢框架结构倒塌时间易损性曲线的拟合方法，并根据结构倒塌时间的可靠指标对结构倒塌性能进行定量评估；最后，采用提出的简化评估方法对火灾下钢框架结构抗倒塌性能进行评估，研究起火房间位置以及防火保护对结构抗倒塌性能的影响.

1 子结构模型的选取及边界条件

子结构模型的选取范围主要考虑火灾影响区域和结构倒塌模式2个因素.根据之前的整体钢框架结构火灾时程分析[5]，单一房间起火在水平方向上主要影响起火房间相邻一跨内的区域，在竖向方向上主要影响上、下一层范围内的结构.同时，子结构模型应体现出室内火灾下结构的倒塌模式.室内火灾下结构的倒塌范围主要包括起火房间和起火房间相邻房间所在的区域.因此，子结构模型在水平方向上可选取起火房间及其相邻一跨半区域，在竖向上可选取起火房间及其上、下各一层半的区域.对于钢框架结构，其底层角部房间起火时的子结构有限元模型示意图见图1.

子结构模型的边界条件主要包括边界约束条件和边界荷载条件.本文采用矩阵分析方法推导子结构模型边界条件的确定方法.推导过程如下：整体结构模型可分为子结构模型和剩余结构模型2个部分.在进行结构分析时，整体结构模型的刚度矩阵K可看作子结构模型刚度矩阵Ks和剩余结构模型刚度矩阵Kr之和.有限元分析时，子结构模型的矩阵平衡方程可写为以下形式：

图1 角部房间火灾下钢框架子结构有限元模型示意图

(1)

式中，U1、U2分别为子结构模型内部节点和边界节点的变形向量；Ks,ij为子结构模型刚度矩阵中第i行第j列的子矩阵；Fs,1、Fs,2分别为子结构模型内部节点和边界节点的节点力向量.剩余结构模型的矩阵平衡方程可写为以下形式：

(2)

式中，U3为剩余结构模型内部节点的变形向量；Kr,ij为剩余结构模型刚度矩阵中第i行第j列的子矩阵；Fr,2、Fr,3分别为剩余结构模型边界节点和内部节点的节点力向量.

因此，采用有限元方法确定子结构边界约束条件的方法步骤如下：

①建立整体钢框架结构去除子结构部分后的剩余结构模型.

②将子结构模型与剩余结构模型相连的边界节点固定，选取边界节点的某一自由度施加单位位移，其他节点自由度保持固定，求解施加单位位移节点处的约束反力.

③将约束反力与施加位移的比值作为边界节点在该自由度下的约束刚度.

④选取下一个边界节点自由度，重复步骤②～③，直到得到全部边界节点约束刚度.

子结构模型边界荷载的确定方法如下：

①对整体结构模型进行荷载分析，记录整体模型中子结构边界节点处的内力向量F2以及剩余结构的变形.

②建立剩余结构模型，将步骤①中记录的剩余结构变形施加在剩余结构模型上，计算出Fr,2.

③子结构模型边界荷载向量为F2-Fr,2.

按照上述方法即可得到子结构有限元模型边界节点的位移约束条件和边界荷载.这里提出的子结构模型边界条件计算方法只适用于单一房间发生火灾的情况.究其原因在于单一房间火灾下剩余结构受火灾影响小，可近似认为其对子结构模型边界节点的约束作用不变.

2 基于子结构模型的室内火灾下钢框架抗倒塌性能简化评估方法

根据易损性分析方法，本文基于子结构模型提出了火灾下钢框架结构抗倒塌性能的简化评估方法，其步骤如下：

①根据起火房间位置，确定子结构模型的选取范围，并计算子结构模型的边界约束刚度和边界荷载.

②选取需要研究的随机变量，采用Monte Carlo方法抽取子结构样本.

③建立子结构样本的有限元模型，并采用有限元方法对其进行火灾时程分析.

④对子结构样本的有限元计算结果进行统计分析，得到结构倒塌时间易损性曲线，并计算结构倒塌时间的可靠指标，以此定量评估结构抗倒塌性能.

2.1 子结构模型有限元分析方法和倒塌标准

采用显式动力分析软件LS-DYNA对钢框架子结构模型进行火灾时程分析.其中，子结构模型的边界位移约束采用三维Spring单元模拟，钢梁、钢柱采用三维Hughes-Liu梁单元模拟，混凝土楼板采用组合壳单元模拟.高温下混凝土和钢材的本构模型采用文献[6-7]建议的高温本构模型.

子结构模型在进行火灾时程计算时可分为如下2步：①在子结构模型的楼板上施加竖向荷载，并在子结构模型的边界施加边界荷载；②对子结构模型中火灾影响范围内的构件施加温度荷载，进行火灾时程分析.有限元计算方法的有效性已在前期工作中进行了验证[5].

由于子结构模型取自钢框架结构，故倒塌标准仍采用钢框架结构的倒塌标准.本文采用文献[8]中的规定，考虑钢框架梁悬链线作用的影响，以钢框架梁转角达到12°作为结构发生倒塌的标准.

2.2 结构倒塌时间易损性曲线

火灾下结构倒塌易损性曲线是指火灾时间t下结构发生倒塌的概率函数曲线.本文采用Monte Carlo方法对钢框架分析模型进行随机抽样，根据火灾时程计算得到结构样本的倒塌时间.火灾下结构倒塌易损性曲线可采用下式进行拟合[9]：

(3)

式中，Pcp为火灾下结构的倒塌概率；Ф为标准正态分布概率函数；μln和σln分别为倒塌时间的对数平均值和对数标准差，且

(4)

(5)

式中，N为结构样本数量；tcp,i为第i个样本的倒塌时间.

2.3 火灾下结构倒塌时间可靠指标

在火灾下结构抗倒塌设计中，以倒塌时间作为设计标准，功能函数Z为

Z=tcp-tdm

(6)

式中，tcp为结构倒塌时间；tdm为结构需求时间.

根据功能函数(6)，火灾下结构倒塌时间的可靠指标β为

(7)

式中，μcp和σcp分别为倒塌时间tcp的均值和标准差；μdm和σdm分别为需求时间tdm的均值和标准差.

3 算例分析

3.1 钢框架模型和防火保护

选用Cardington试验中的8层钢框架办公楼作为研究模型，结构平面布置见图2.图中，A3为受火钢柱.结构层高4 m，共8层.结构的角柱、边柱、中柱截面尺寸分别为H260 mm×256 mm×10 mm×17 mm、H320 mm×309 mm×14 mm×22 mm、H340 mm×315 mm×19 mm×31 mm，钢梁截面尺寸为H351 mm×171 mm×7 mm×12 mm.楼板采用钢筋混凝土板，厚度为100 mm.楼板中钢筋的直径和间距分别为10和150 mm.框架梁、柱的钢材等级为S275，钢材的弹性模量和屈服强度分别为210 GPa和275 MPa.楼板采用C30混凝土和HPB300钢筋.钢框架楼板承受的永久荷载为4.94 kPa，可变荷载取为2.5 kPa.根据文献[10]，分析时荷载组合采用永久荷载和0.5倍可变荷载的组合.

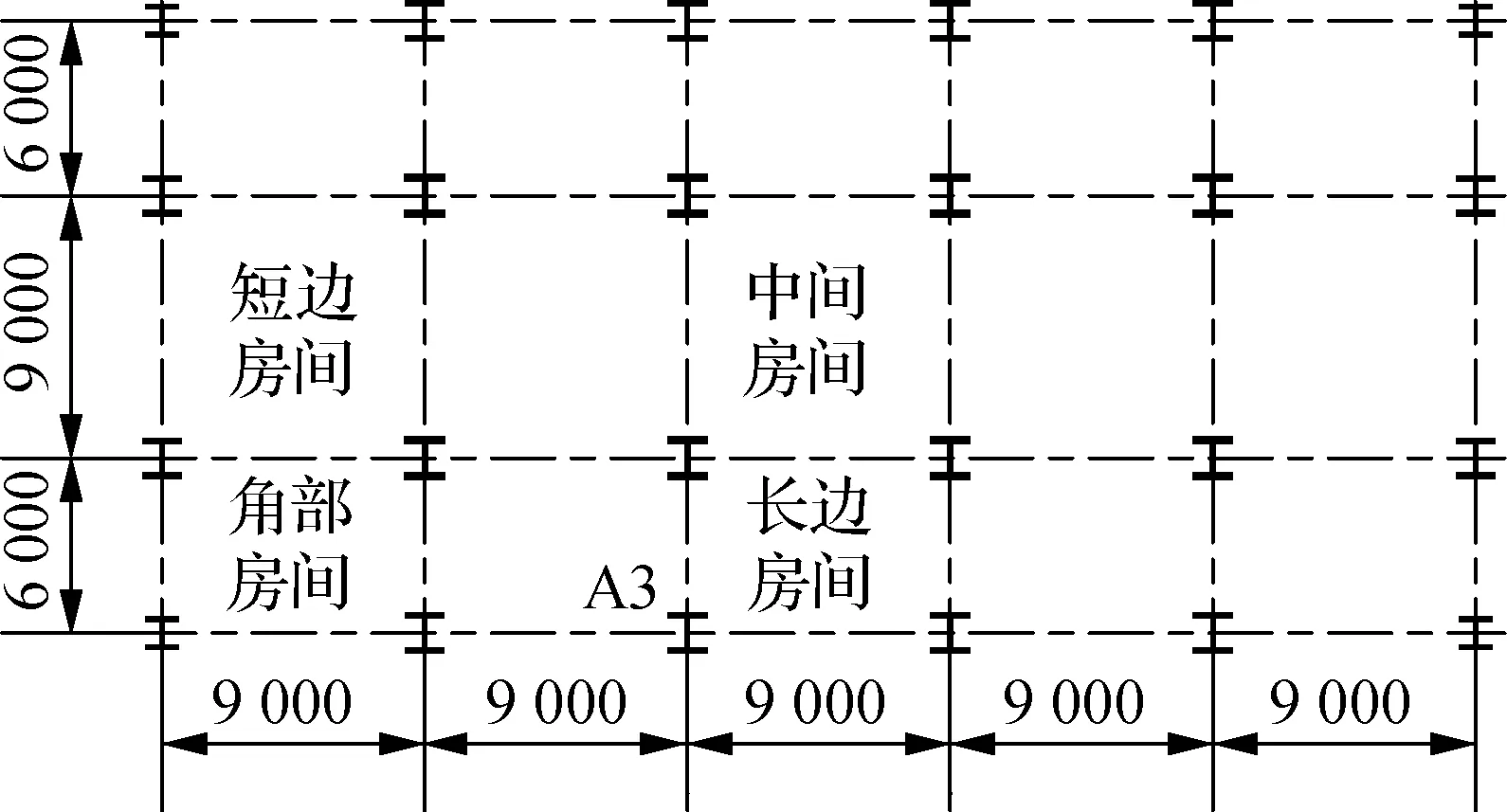
图2 钢框架结构平面布置图 (单位：mm)

根据防火设计规范要求，钢结构需进行防火保护.本文共考虑了以下3种防火保护类型：①高防火保护，即柱保护时间为3 h，梁保护时间为2 h；②中防火保护，即柱保护时间为2 h，梁保护时间为1.5 h；③低防火保护，即柱保护时间为1 h，梁保护时间为1 h[11].在这3种防火保护条件下，钢框架的倒塌需求时间分别为3、2、1 h.构件的防火保护材料采用CAFCO300，该防火材料的导热系数为0.078 W/(m·K)，密度为240 kg/m3.高防火保护条件下，钢梁和钢柱的防火保护层厚度分别为4.9和3.2 cm；中防火保护条件下，钢梁和钢柱的防火保护层厚度分别为3.7和2.2 cm；低防火保护条件下，钢梁和钢柱的防火保护层厚度分别为2.3和1.3 cm.起火房间选在结构底层的角部房间、短边房间、长边房间以及中间房间.火灾的升温曲线选用ISO834标准升温曲线.

研究的随机变量包括钢材的屈服强度、弹性模量、混凝土抗压强度、钢筋屈服强度、钢柱的防火涂层厚度以及钢梁的防火涂层厚度.根据随机变量的分布研究[12-13]，各随机变量的分布规律以及基本统计数据如表1所示.

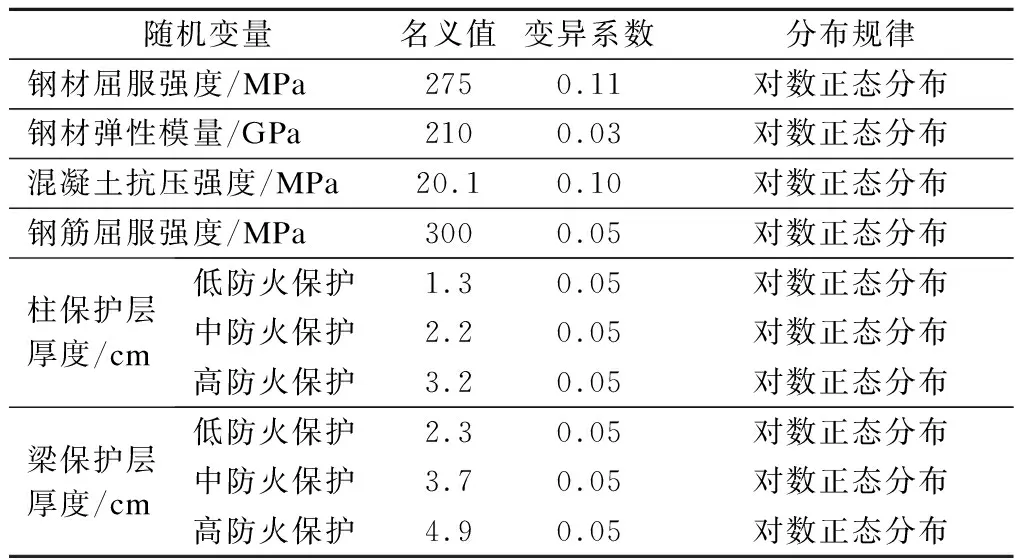
表1 随机变量基本统计数据表

3.2 子结构模型验证

采用钢框架整体结构的有限元分析结果对子结构模型进行验证，以长边房间发生火灾作为验证工况.采用子结构模型得到的受火钢柱A3的轴力以及柱顶竖向位移与整体结构模型计算结果对比如图3所示.由图可知，子结构模型得到的火灾下结构内力和变形的变化与整体结构模型计算结果差别不大.由图4可知，根据2种分析模型得到的结构倒塌模式相同.子结构模型得到的结构倒塌时间为1.22 h，整体结构模型得到的结构倒塌时间为1.25 h，即子结构模型得到的结构倒塌时间略小于整体结构模型.

由此可见，所提的子结构模型选取范围和边界条件确定方法是合理的，子结构模型的精确性满足计算要求.此外，相同计算条件下，子结构模型所需计算时间为25 min，而整体结构模型需要200 min，即采用子结构模型可以节省大量计算时间.

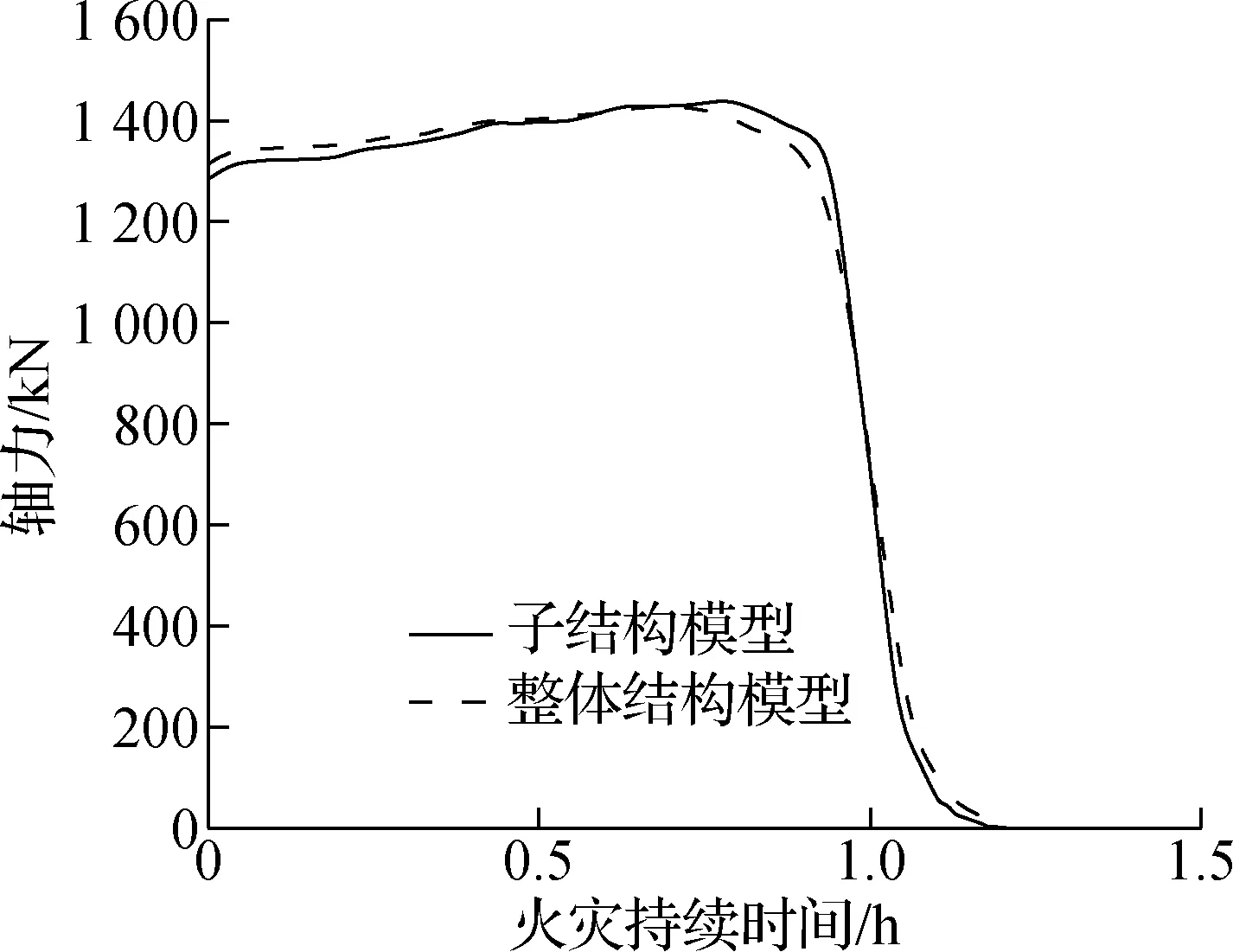
(a) 轴力

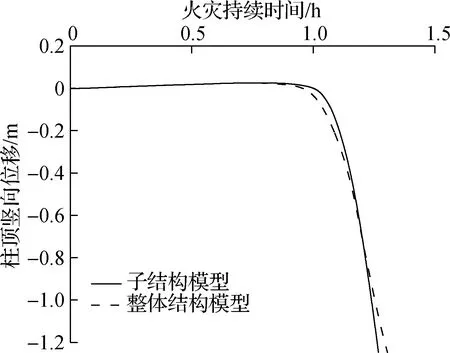
(b) 柱顶竖向位移

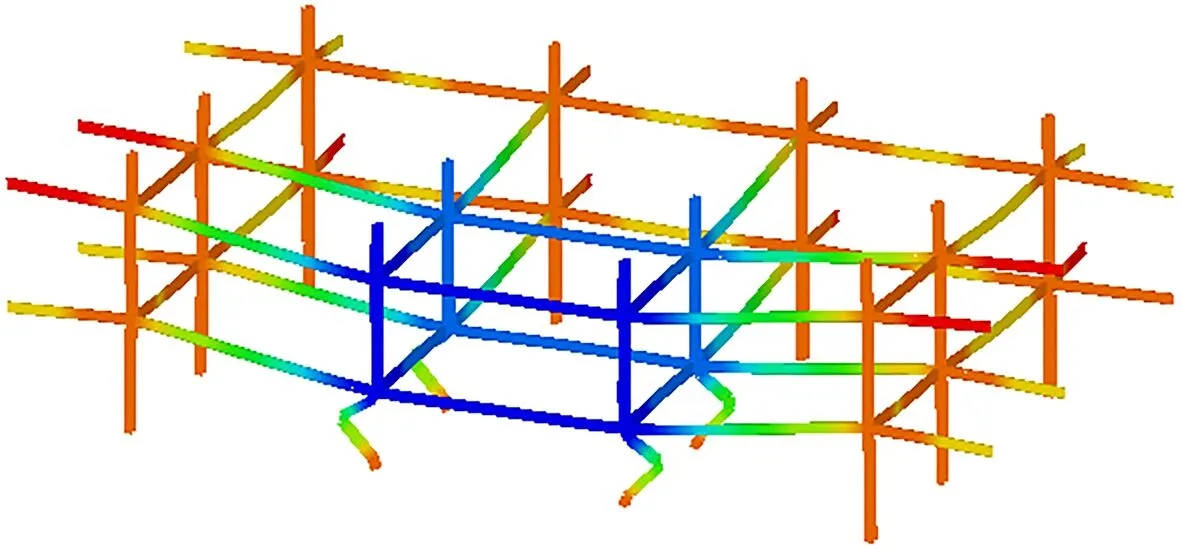
(a) 子结构模型

(b) 整体结构模型

3.3 钢框架倒塌性能评估

本文共研究了12种工况，包括4种起火房间位置(角部房间、短边房间、长边房间和中间房间)和3种防火保护(低、中、高)的组合.采用Monte Carlo方法对子结构模型进行抽样，每种工况抽取200个样本.

3.3.1 起火房间位置的影响

不同房间发生火灾的工况下结构倒塌时间易损性曲线见图5，结构倒塌时间的统计参数见表2.由图5可以看出，相同防火保护条件下，由于起火房间位置的不同，结构的倒塌概率也不相同.同时，相同倒塌概率下，角部房间以及短边房间发生火灾时，结构的倒塌时间相对较短；而在长边房间以及中间房间发生火灾时，结构的倒塌时间较长.这主要是因为角部房间和短边房间的冗余约束相对较少，结构难以形成稳定的悬链线机制，结构更容易发生倒塌；而长边房间和中间房间的冗余约束相对较多，结构在受火钢柱失效后可以形成稳定的悬链线机制，从而延缓结构的倒塌.因此，可初步认为框架结构的角部房间以及短边房间发生火灾是结构抗火设计中较危险的火灾工况.此外，根据表2中的标准差数据可以看出，在相同防火保护条件下，不同室内火灾工况下结构倒塌时间的标准差差别不大，说明起火房间位置对结构倒塌时间的离散性影响不大.

3.3.2 防火保护的影响

根据表2中结构倒塌时间统计数据可以发现，低、中、高防火保护条件下各火灾工况中具有95%保证率的结构倒塌时间最大差距分别为0.12、0.18、0.22 h.由结构倒塌时间标准差的变化规律可知，随着防火保护的提高，结构倒塌时间的标准差也增加.究其原因在于随机变量分布规律相同，高防火保护条件下结构防火涂层厚度的变化较大，结构受火构件的温度变化也较大，从而导致结构倒塌时间的离散性较大.由此可见，高防火保护条件下结构倒塌时间受随机变量的不确定性影响更大.因此，在对结构进行防火设计时，应该对高防火保护条件下的结构采用更加严格的构造要求和检验标准，减少随机变量的随机性对结构火灾下倒塌时间的影响，保证火灾下结构的抗倒塌能力.

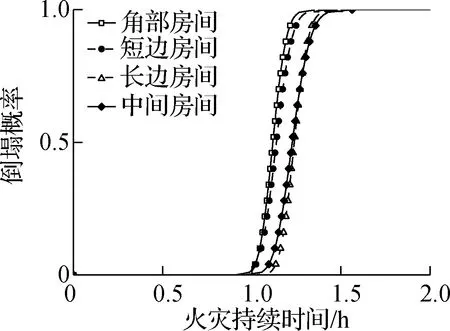
(a) 低防火保护

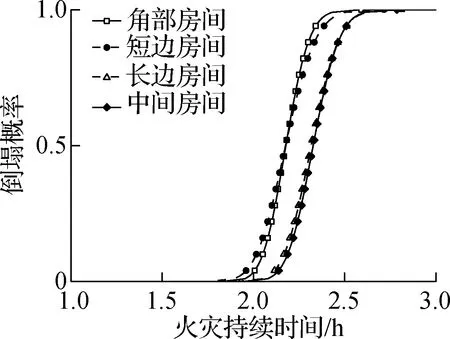
(b) 中防火保护

(c) 高防火保护

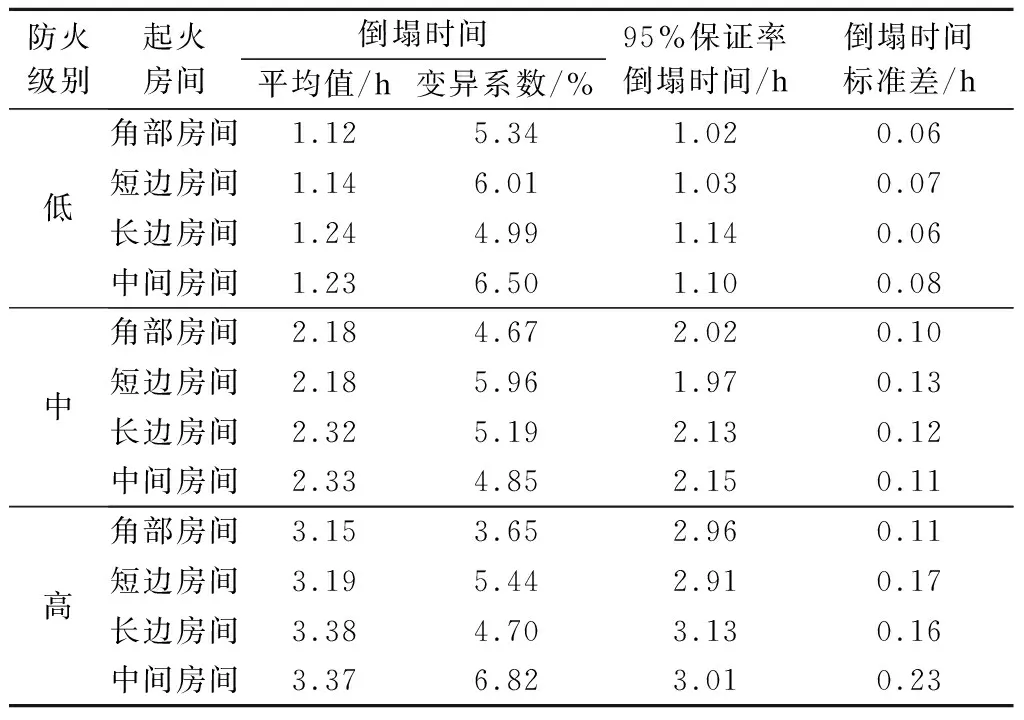
表2 随机变量基本统计数据表

3.3.3 结构倒塌可靠指标

根据表2中结构倒塌时间的统计参数，采用式(7)计算结构倒塌时间的可靠指标，结果见表3.由表可知，角部房间和短边房间发生火灾时结构倒塌时间的可靠指标较低，说明其对结构抗倒塌性能更不利.

结构设计中通常会规定结构的目标可靠指标.根据《建筑结构可靠性设计统一标准》(GB 50068—2018)[14]，安全等级为二级的房屋建筑结构发生延性破坏和脆性破坏时的目标可靠指标分别为3.2和3.7.由表3可见，大部分工况下结构倒塌时间可靠指标为1.0～3.0.因此，在进行火灾下结构抗倒塌设计时，为保证结构设计满足可靠指标要求，室内火灾下钢框架结构的倒塌时间应除以大于1的分项系数.

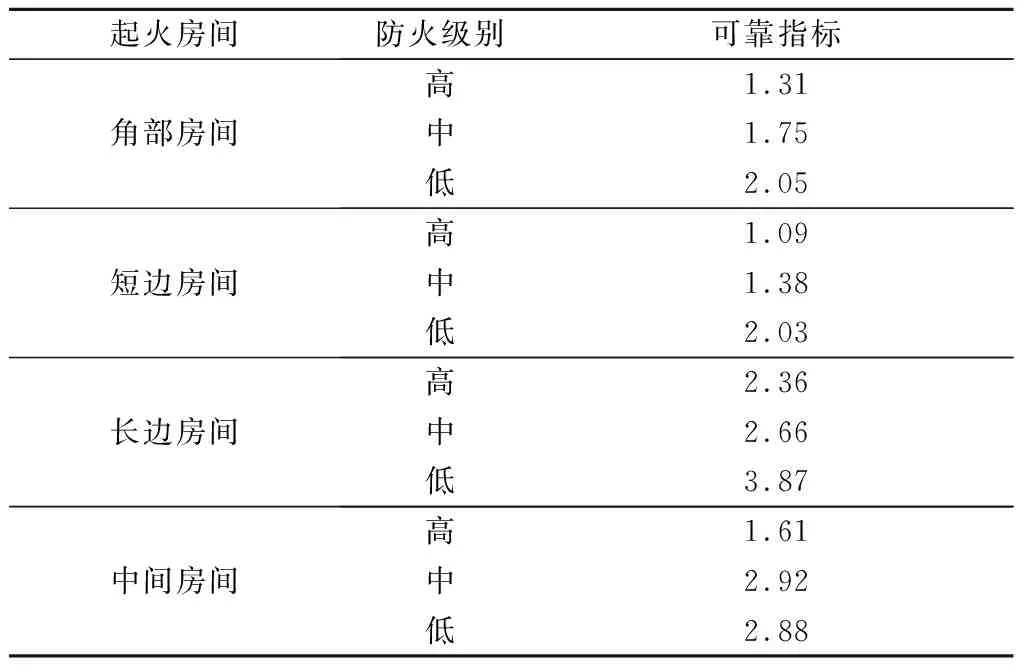
表3 结构倒塌时间可靠指标

4 结论

1) 根据室内火灾下的影响区域确定子结构模型的选取范围，通过矩阵分析方法提出子结构模型边界条件的确定方法，并采用整体结构模型计算结果对子结构模型进行了验证.结果表明，子结构模型能够较好地反映结构内力和变形的变化，体现结构倒塌模式.这说明提出的子结构模型选取范围和边界条件确定方法是合理的.对比2种模型的计算时间可以发现，采用子结构模型可以节省大量计算时间.

2) 根据易损性分析方法，提出了一种基于子结构模型的室内火灾下钢框架结构倒塌性能简化评估方法，并对三维钢框结构进行了火灾下倒塌性能评估.结果发现，钢框架的角部房间以及短边房间发生火灾对结构火灾下倒塌影响最大.结构在这些位置处的冗余约束较少，钢柱失效后很难形成稳定的悬链线机制.通过对防火保护研究发现，相同随机变量分布规律下，高防火保护条件下结构倒塌时间受随机变量的不确定性影响更大.因此，在结构抗火设计中，高防火保护结构应该采取更加严格的检验标准.

3) 火灾下结构倒塌时间的可靠指标主要分布在1.0～3.0范围内，小于规范要求的目标可靠指标.在进行抗火设计时，室内火灾下钢框架结构的倒塌时间应除以大于1的分项系数，以保证结构设计满足目标可靠指标.