壁面厚度和材料对微通道内H2/空气燃烧特性影响的数值模拟

赵 亮，安江波

(海军士官学校机电系，蚌埠 233012)

现阶段各种便携式电子设备以及微小型无人机的快速发展，化学电池的使用范围越来越广泛，但是化学电池存在着持续时间短、能量密度低、充电时间长等缺点[1].而碳氢燃料电池其能量密度(40 MJ/kg)是传统化学电池(0.5 MJ/kg)的数十倍[2]，因此可以使用基于燃烧的微型发电技术作为常规化学电池的替代品[3-4].为了开发微型燃烧器，必须克服诸如热损失、火焰淬熄、摩擦损失等问题[5]，而这些问题的产生原因是多方面的.首先，微燃烧器的面体比相对于常规燃烧器而言增大了两个数量级，这使得通过壁面的热损失大大增加[6].而且由于面体比的增大，也会提高反应自由基与壁面碰撞而销毁的可能性.其次，由于微燃烧器几何尺寸变小，导致了气体混合物在燃烧器内停留时间变短，化学反应不充分[7].此外，对于直通道微燃烧器，如果进气速度过大，燃料混合气体无法维持稳定燃烧，便被吹熄[8].目前，微小尺度下的火焰稳燃方法主要有以下几种：①采用催化燃烧.Fu 等[9]在微型燃气透平表面附着催化剂，能够有效地降低燃烧温度和热量损失.②对微燃烧室表面进行惰性化处理.Miesse 等[10-11]对燃烧室表面进行化学处理，以减少对活性自由基的捕获.③采用特殊的结构设计.Kuo 等[12]采用螺旋形状的“瑞士卷”(Swiss-roll)结构，使未燃燃料在流动过程中被燃烧产生的高温加热，起到了预热、稳燃的目的.④基于回流区稳燃.Fan 等[13]在燃烧室内部采用凹腔或者钝体的方式，可以有效地提高火焰燃烧的稳定性.

Norton 等[14]对二维平板微燃烧器内CH4/空气预混气体的燃烧进行了数值模拟，结果表明壁面厚度和热导率对于沿着平板向上游传递热量有着很重要的作用，但是对于壁面厚度和材料对预混燃烧特性的影响没有进行深入研究.本文拟通过数值模拟的方法对二维平板微燃烧器内H2/空气预混燃烧特性进行了研究，并对壁面厚度和热导率对火焰位置、外壁面温度、燃烧效率、热循环比和散热损失比的影响进行了研究.

1 数值模拟方法

1.1 几何模型

平板微燃烧器的示意图如图1 所示.燃烧室上下平板间距H＝1 mm，平板微燃烧器总长度L＝10 mm，平板厚度δ为0.2 mm、0.4 mm，整个平板微燃烧器采用二维结构，上、下平板对称布置.

图1 平板微燃烧器结构Fig.1 Structure of planar micro-combustor

1.2 计算方法

为了研究壁面材料对微燃烧器内火焰稳定性的影响，选择石英和碳化硅(SiC)作为微燃烧器的壁面材料.第一个原因是这两种材料可以承受较高的温度(大于1 700 K).另一个原因是，碳化硅的热导率约为石英玻璃的30 倍，而它们的表面发射率几乎相同，这有助于研究壁面热传导对火焰稳定性的影响.平板固体材料选用石英和碳化硅，其300 K 条件下的物性参数如表1 所示.

表1 石英和碳化硅300 K条件下的物性参数Tab.1 Physical properties of quartz and silicon carbide at 300 K

首先，计算了Knudsen 数，其计算方法如式(1)所示.

式中：Lg为气体混合物的平均自由程；Lc为通道的特征尺度.

计算表明，在本次模拟中，Knudsen 数远低于0.001[15].因此，反应流体可以看作是连续的，Navier-Stokes 在这里仍然适用.此外，由于本次模拟中最大雷诺数约为1 700，加上是笔直的微通道结构，因此在数值模拟中采用了层流模型.

本文模拟的最大雷诺数为1 700，虽然根据Kuo等[12]的建议，对于具有螺旋通道的瑞士卷微燃烧器，雷诺数大于500 时，在模拟时应该采用湍流模型进行数值模拟.但是，该准则并不适用于笔直的微通道.因此，在本研究的数值模拟中采用了层流模型，其正确性将在后面进行验证.在计算中，控制方程如下所示：

连续性方程：

动量守恒方程：

能量守恒方程：

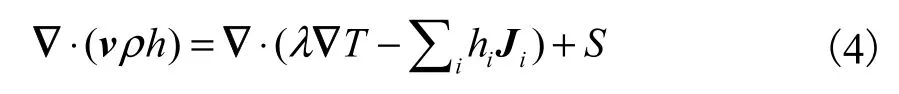
组分守恒方程：

式中：v、p、ρ、τ、λ、h 和T 分别代表气体混合物的速度、压力、密度、应力张量、热导率、比焓和温度；S代表化学反应热；Yi、hi和Ri分别代表第i 种物质的质量分数、比焓和生成或者消耗率；Ji为扩散通量.

在计算中，还考虑了微燃烧器的壁面导热，其计算方法如式(6)所示.

式中：λs为固体壁面的热导率；Ts为固体壁面的温度.

在微燃烧器的入口，三维和二维模型都使用当量比为1 的H2/空气的预混气体，进气温度为300 K.进口采用速度入口边界条件，出口采用压力出口边界条件.平板微燃烧器的内壁面为无滑移壁面，内壁面之间的辐射使用离散坐标(DO)模型[17].微燃烧器外壁面的散热损失速率通过式(7)计算.

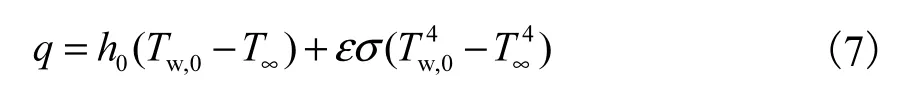
其中，由于燃烧器表面温度较高，基于传热学教材上给出的经验公式进行计算，得知自然对流换热系数h0约为20 W/(m2·K)；Tw,0为平板微燃烧器外壁面的温度；T∞为环境温度，其值取300 K；ε为平板微燃烧器外壁面的法向发射率，σ＝5.67×10-8W/(m2·K4)为Stefan-Boltzman 常数.

氢气与空气的气相反应机理采用Li 等提出的包含13 种组分、19 种可逆反应的反应机理[18].由于采用了层流模型，因此燃烧模型选择层流有限速率模型.使用Gambit 对计算域进行网格划分，采用二阶迎风格式对微分方程组进行离散，并基于“SIMPLE”算法对压力和速度进行耦合.使用Maxwell-Stefan 方程计算多组分扩散.

使用各组分比热的质量分数加权平均法计算混合物的比热，同时假设混合气体是不可压缩的理想气体，从而获得混气体的密度.使用CFD 软件Fluent15.0求解质量守恒、动量守恒、能量守恒和组分守恒方程.

计算前对网格独立性进行验证，如图2 所示.从图2 可见，网格数分别为35 000 和62 000 时，沿微通道燃烧器中心线的温度分布基本相同，因此本文最终所选取的网格数为 35 000，其尺寸大小为Δx ＝0.02mm，Δy＝0.02 mm.

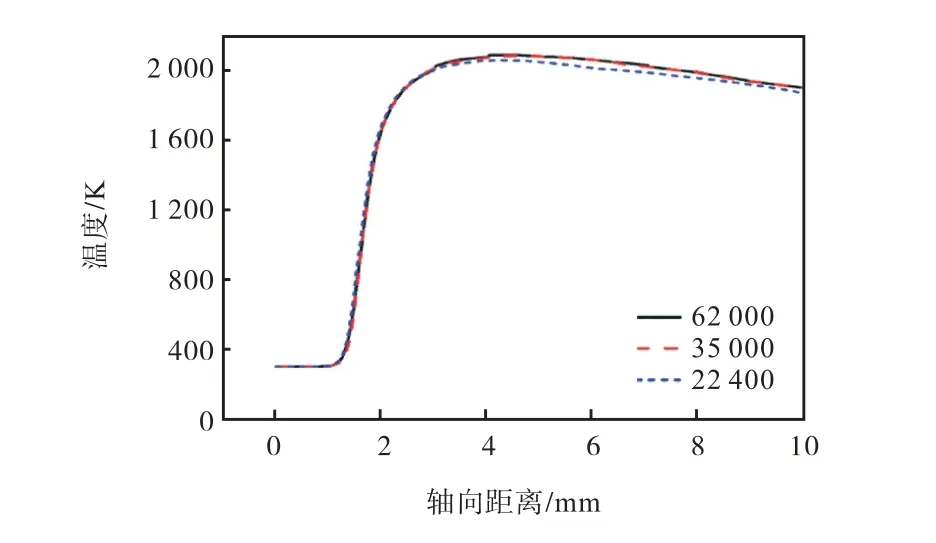
图2 Vin＝6 m/s 不同网格数时计算所得的平板微燃烧器中线温度分布Fig.2 Central line temperature distribution of planar micro-combustor calculated with different grid numbers at inlet velocity of 6 m/s

为了验证本文所采用的数值模拟方法的正确性，对文献[19]中的试验工况进行了数值模拟.该实验工况同样使用平板型微燃烧器，通道高度为2 mm，通道宽度为8 mm，壁面厚度为0.5 mm，壁面材料为316 不锈钢，在该实验工况中，仍然使用的是氢气和氧气的预混气体，进气流量为200 mL/min，因此，该燃烧器处于层流工况，所以，使用文献[19]中的试验工况对本文的模拟方法和计算结果进行验证是可靠的.如图3 所示，将模拟获得的外壁面温度分布和试验测量值进行对比，其最大误差为6.38%，说明本文所采用的模拟方法具有比较高的精度.

图3 数值模拟方法的实验验证Fig.3 Experimental verification using numerical simulation method

2 结果与讨论

2.1 计算结果

图4、图5 所示分别为不同材料、不同厚度时，不同速度下的温度云图.由图4 可以看出，平板材料为石英时、当进气速度Vin＝1 m/s 时，微燃烧器内的的高温区域位于预混气体进口附近，且高温区域呈“V”型，并在靠近进口一侧呈现扁平状，说明此时火焰锋面为扁平状.当Vin增大到6 m/s 时，微燃烧器内的高温区域逐渐扩大，且高温区域逐渐向下游移动，而火焰锋面逐渐开始弯曲，当Vin达到6.3 m/s 和8.1 m/s 时，不同壁厚的燃烧器内部温度场不再上下对称，即微燃烧器内火焰发生偏斜，此时燃烧器内火焰无法保持稳定，经过多次计算验证，这种火焰偏斜现象的出现是随机的.平板材料为碳化硅时，由图5可以看出，壁厚为0.2 mm、进气速度达到16.1 m/s时，微燃烧器内火焰发生偏斜；而当壁厚为0.4 mm时，火焰没有发生偏斜，一直保持对称状态.Pizza等[16]在详细化学反应机理和固定壁温分布的边界条件下，通过直接数值模拟(DNS)发现了类似现象，并命名为“V-型”火焰和偏斜火焰，这也证明了本文数值模拟的正确性.

图5 平板材料为碳化硅时不同厚度下的温度云图Fig.5 Temperature distributions of silicon carbide with different wall thicknesses

图6 不同材料和壁厚时的火焰偏斜极限和吹熄极限Fig.6 Deflection limit and blow-off limit of flame with different materials and different wall thicknesses

本文定义燃烧器内火焰开始发生偏斜时的进气速度为偏斜极限，则相对应的偏斜极限如图6(a)所示.图6(b)所示为不同壁厚、不同材料条件下微燃烧器的吹熄极限，由图6(b)可以看出，相同材料的平板厚度越大，其吹熄极限就越大；同样地，相同厚度的平板，碳化硅的吹熄极限要比石英的吹熄极限大得多.

定义火焰位置为火焰未发生偏斜时平板燃烧器内OH 组分浓度最大的位置.图7 给出了材料为石英、δ＝0.2 mm 和δ＝0.4 mm 时火焰位置；图8 给出了δ＝0.2 mm、不同材料条件下的微燃烧器内火焰的位置.由图7、图8 可以看出，随着进气速度的增大，火焰位置逐渐向燃烧器的下游移动.如图7 所示，在进气速度为低速(Vin≤4 m/s)时，不同厚度的平板微燃烧器内部火焰位置接近于重合，而当Vin≥4 m/s时，随着进气速度的不断增大，0.2 mm 厚度相比较0.4 mm 厚度的燃烧器其火焰位置更靠近下游；同样地，如图8 所示，在进气速度为低速(Vin≤3 m/s)时，不同材料的平板微燃烧器内部火焰位置接近于重合，而当Vin≥3 m/s 时，随着进气速度的不断增大，石英材料的平板微燃烧器相对于碳化硅材料其火焰位置更靠近下游.这是因为，当进气速度较低时，燃料的反应区域靠近燃烧器的进口处，其通过平板向上游的回热量很小，对气体的预热效果不足，而当进气速度增大时，燃料的反应区逐渐向下游移动，其通过平板向上游的回热量主要受到平板的热阻的影响，而平板的热阻与其热导率成反比，并且随着平板厚度的增大，热量通过平板向燃烧器上游回热的通道面积也会随之增大，因此，厚度越大、热导率越高(碳化硅的热导率远大于石英的热导率)的燃烧器向上游传递的热量也就越多，对气体的预热效果也就越好，其火焰位置也就越靠近燃烧器的上游.

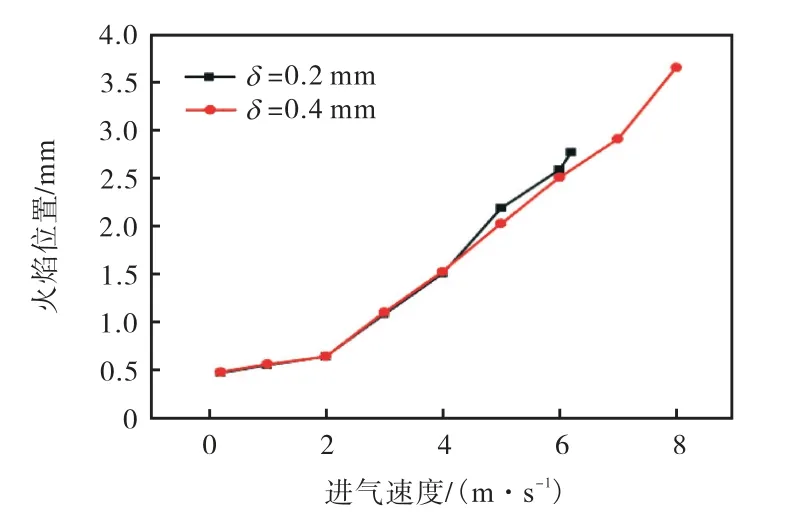
图7 材料为石英时不同厚度条件下的火焰位置Fig.7 Flame location of quartz at different wall thicknesses

图8 δ＝0.2 mm时不同材料条件下的火焰位置Fig.8 Flame location with different wall material at δ＝0.2 mm

图9 给出了进气速度Vin＝6 m/s 时平板材料为石英、不同厚度条件下的外壁面温度分布.图10 为Vin＝6 m/s、平板厚度为0.2 mm 时不同材料条件下的平板外壁面温度分布.由图可以看出，外壁面温度分布呈现出由燃烧器进口到出口先上升再下降的过程.壁面温度的上升是由氢气的化学反应机理决定的，当气体进入燃烧器时，反应不会立即发生，反应物要吸收热量分解从而生成中间产物，最后再生成最终产物.而温度的下降则是由于壁面向外散热引起的.同时，由图10 可以看出当平板材料为碳化硅时，其壁面温度分布更加均匀，其壁面最高温度和最低温度只相差100 K，这主要是因为碳化硅的热导率(32.8 W/(m·K))远大于石英的热导率(1.05 W/(m·K))，这使得燃烧器内部向上下游传递的热量更多，从而使外壁面温度分布更加均匀.

图9 Vin＝6 m/s、材料为石英时不同厚度条件下的外壁面温度分布Fig.9 Temperature distribution of outer wall with different wall thicknesses of quartz and Vin＝6 m/s

图10 Vin＝6 m/s、δ＝0.2 mm 时不同材料条件下的外壁面温度分布Fig.10 Temperature distribution of outer wall with different wall materials at Vin＝6 m/s and δ＝0.2 mm

图11 为材料为石英、不同厚度条件下的燃烧效率；图12 给出了平板厚度δ＝0.2 mm、不同材料条件下的燃烧器燃烧效率.由图11、图12 可以看出，随着进气速度的增大，燃烧器的燃烧效率都呈现出先升高再降低的过程，这是因为当进气速度较低时，燃料的燃烧速率也比较低，燃料在短时间停留内能够燃烧的量毕竟有限，随着进气速度的增加，燃料的燃烧速率也随之增加，其燃烧效率也随之增大，一直到燃烧效率达到极限值；但是伴随着进气速度的进一步增加，燃料在燃烧器内停留的时间越短，使得未能燃烧的燃料量也随之增大，燃烧效率逐渐变低.由图11可以看出，当进气速度Vin≤7 m/s 时，两者燃烧效率的变化趋势基本一致，而当Vin＞7 m/s 时，两者的燃烧效率急剧下降，但是平板厚度δ＝0.2 mm 时的下降幅度比δ＝0.4 mm 时的下降幅度更大；同样地，由图12 可以看出，当进气速度Vin≤8 m/s 时，两种材料的燃烧效率的变化趋势基本一致，而当Vin＞8 m/s 时，石英材料的燃烧器燃烧效率急剧下降，而碳化硅材料的燃烧器的燃烧效率仍然保持一个平缓的下降趋势.这主要是因为随着进气速度的增大，燃烧器内部的高温区也随之向下游移动，从而导致沿着平板向上游传递的热量也随之减少，对进口处气体的预热效果也随之降低，但是因为碳化硅的热导率远大于石英的热导率，因此沿着平板向上游传递的热量也就越多，从而导致了其燃烧效率的变化趋势更为平缓.

图11 材料为石英时不同厚度条件下的燃烧效率Fig.11 Combustion efficiency with different wall thicknesses of quartz

图12 δ＝0.2 mm、不同材料条件下的燃烧效率Fig.12 Combustion efficiency with different materials at δ＝0.2 mm

2.2 结果分析

2.2.1 壁面厚度和材料对热循环比的影响

图13 材料为石英时不同厚度条件下的热循环比Fig.13 Heat recirculation ratio with different thicknesses of quartz

图14 δ＝0.2 mm、不同材料条件下的热循环比Fig.14 Heat recirculation ratio with different materials at δ＝0.2 mm

图13 给出了材料为石英时不同厚度条件下的热循环比；图14 给出了壁面厚度δ＝0.2 mm、不同材料条件下的热循环比.本文定义热循环比为：通过上游内壁面传递给未燃预混气的热量与输入微燃烧器能量的比值.如图13 所示，两种壁面厚度条件下，热循环比随着进气速度的增大而不断下降，并且壁面厚度δ＝0.2 mm 时的热循环比下降速度更快.例如，当进气速度Vin＝1 m/s 时，两种厚度条件下的热循环比基本相同，而当进气速度Vin＝6 m/s 时，δ＝0.2 mm 的燃烧器的热循环比为2.89%，而δ＝0.4 mm 的燃烧器的热循环比为7.13%.这是由于壁面厚度的增加，使得热量流通面积增大，从而通过平板向上游传递的热量增多.如图14 所示，在δ＝0.2 mm 时，两种不同材料的燃烧器进行对比，可以发现随着进气速度的增大，热循环比仍然呈现出下降的趋势，同时碳化硅材料的燃烧器的热循环比要远大于石英材料，这是因为为碳化硅的热导率是石英热导率的30 倍，同样条件下，碳化硅材料向上游传递的热量更多，对进口处气体的预热效果也就更好.

2.2.2 壁面厚度和材料对散热损失比的影响

图15 给出了材料为石英时不同厚度条件下的散热损失比；图16 为壁面厚度δ＝0.2 mm、不同材料条件下的散热损失比.本文中散热损失比的定义为：单位时间内从燃烧器表面散失的热量与进入燃烧器的总能量之比.如图15 所示，随着进气速度的增大，燃烧器的散热损失比呈现出下降趋势，并且当Vin≤6.3 m/s 时，δ＝0.2 mm 的燃烧器的散热损失比大于δ＝0.4 mm 的燃烧器，但是当Vin＞6.3 m/s 时，δ＝0.2 mm 的燃烧器的散热损失小于δ＝0.4 mm 的燃烧器，且当Vin＞6.3 m/s 时，δ＝0.2 mm 的燃烧器的散热损失比开始急剧下降，而当 Vin＞8.1 m/s 时，δ＝0.4 mm 的燃烧器的散热损失比才开始急剧下降.图16 中也呈现出了同样的规律，只是当Vin＞16.1 m/s时，SiC 材料的燃烧器的散热损失比才开始急剧下降.如图6(a)所示，Vin＝6.3 m/s、Vin＝8.1 m/s 时，Vin＝16.1 m/s 分别是3 种不同工况的燃烧器内火焰的偏斜极限，也就说明，当燃烧器内的火焰开始偏斜时，其散热损失比也会发生剧烈变换.这种现象的产生主要与燃烧器内的火焰温度有关，如图17、图18所示，燃烧器内的火焰温度随着进气速度的增大而升高.当进气速度达到偏斜极限时，例如δ＝0.2 mm、石英材料的燃烧器当Vin＞6.3 m/s 时，燃烧器内的温度开始下降，相对应地它的散热损失比也开始急剧下降.

图15 材料为石英时不同厚度条件下的散热损失比Fig.15 Heat loss ratio with different thicknesses of quartz

图16 δ＝0.2 mm、不同材料条件下的散热损失比Fig.16 Heat loss ratio with different materials at δ＝0.2 mm

图17 材料为石英时不同厚度条件下的火焰温度Fig.17 Flame temperature with different thicknesses of quartz

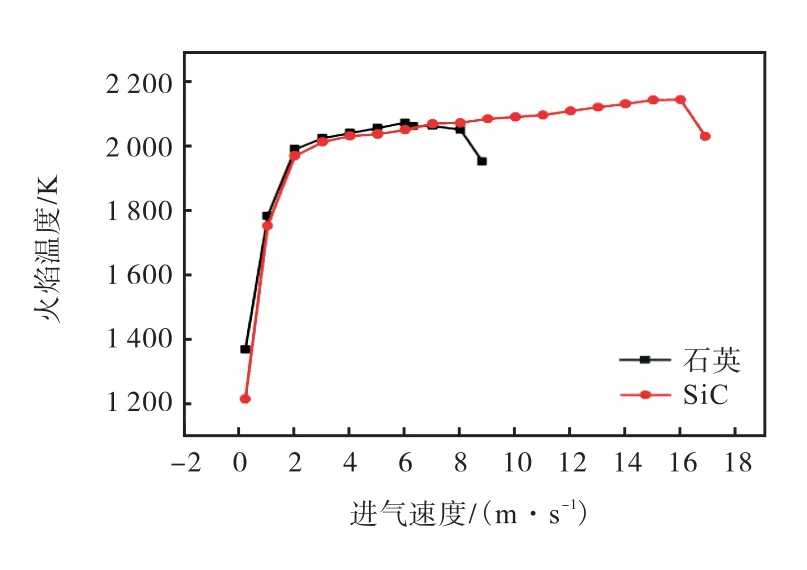
图18 δ＝0.2 mm、不同材料条件下的火焰温度Fig.18 Flame temperature with different materials at δ＝0.2 mm

3 结论

通过数值计算对二维平板燃烧器内H2/空气的预混燃烧特性进行了研究，讨论了壁面厚度和材料的影响，可以得出以下结论.

(1) 对比相同状态下火焰的吹熄极限和偏斜极限，发现平板材料的热导率越高、平板厚度越大，火焰的稳定性就越好，吹熄极限和偏斜极限就越大.

(2) 平板厚度越大、热导率越高，火焰位置越靠近燃烧器的上游，且平板外壁面温度分布更加均匀、燃烧效率和热循环比更高.

(3) 燃烧器的散热损失比受到火焰温度的影响，并随着火焰温度的升高而降低，但是当进气速度达到偏斜极限时，燃烧效率和火焰温度开始下降，从而导致燃烧的散热损失比开始急剧下降.