基于GSA-BP神经网络的GNSS高程拟合方法

张建奇

(广州市城市规划勘测设计研究院, 广东 广州 510000)

0 引言

近年来随着国民经济和国家生产总值的不断提高,各种高铁隧道,桥梁大坝等利国利民市政工程不断开工建设,在目前二维平面测量精度已达毫米量级的情况下,高程测量精度对工程建筑质量具有重大影响。当前国际高程系统分为正高、正常高和大地高,我国实际工程应用中大量采用以铅垂线和近似水准面为基准的正常高H,而全球定位系统测得的是以法线和参考椭球面为基准的大地高h,两者之间存在高程异常:ξ=H-h。正常高数据的获取和使用需要根据几何水准测量,存在观测效率低,测量精度受地形影响大的问题,而大地高数据的获取是通过全球导航卫星系统(Global Navigation Satellite System，GNSS)相对静态定位方式,具有全天时,全天候,使用方便和高精度的优势,因此如何将大地高转换为工程实践中所需的正常高,即求出两者之间的高程异常ξ对于市政工程建设具有重要意义,也是当前研究的热点问题[1-2]。

目前最常用的GNSS高程拟合方法是根据部分已知观测水准点的高程异常值,采用多项式拟合,曲面拟合等方法对未知观测点的高程异常进行插值计算,该类方法的拟合性能受GNSS观测水准点的分布影响较大,仅适合于GNSS水准点分布均匀,地势平坦的地区[3-4];随着数值计算和优化理论的发展,小波变换,AIC准则和支撑向量机等方法逐渐被应用于GNSS高程拟合领域,文献[5]利用小波方法对GNSS连续观测上海站的GNSS高程数据随时间的变化趋势进行分析,研究了季节变化,地表植被,大气等因素对GNSS高程观测的影响;文献[6-7]利用聚类方法和AIC准则/BIC准则对某矿区的GNSS高程数据进行分析,取得了接近三等水准测量的拟合精度;文献[8]研究了不同地形条件下的GNSS高程拟合问题,提出一种基于地形修正的支撑向量机算法对某D级GNSS控制网进行高程拟合,并获得了优于1 cm的拟合精度;近年来随着人工神经网络技术的兴起,基于神经网络模型的GNSS高程拟合方法由于不依赖于精确的数学模型,数据驱动和自适应性等优点得到了学术界的广泛关注,文献[9]利用BP神经网络模型对湖南省某县区的GNSS高程异常数据进行研究,试验结果表明BP神经网络模型相对于传统曲面拟合法的拟合精度提升50%以上;文献[10]采用径向基函数(Radial Basis Function, RBF)神经网络模型对某市区GNSS网络数据进行研究,并从拟合残差,内外拟合精度等维度对拟合性能进行评估,结果显示RBF神经网络模型的拟合性能优于支持向量机(Support Vector Machine, SVM)方法。上述研究成果表明,神经网络方法相对于传统方法可以获得更高的拟合性能,但是文献[11]的研究表明神经网络模型初始参数的选取对拟合精度影响较大,而目前通常采用的经验试错法存在主观性强,运算复杂和易陷入局部最优解的问题。

本文在上述研究的基础上,针对BP(Back Propagation)神经网络模型的初始参数选取问题,提出一种遗传模拟退火算法(Genetic Simulated Annealing, GSA)优化的BP神经网络模型,该方法利用GSA的全局寻优能力优化BP神经网络模型的学习过程,避免其陷入局部极值的同时提升模型的拟合精度和数据适应性。基于某测区的实测GNSS数据的开展试验,对所提方法的拟合性能进行验证,并将结果与传统BP神经网络模型进行对比。

1 BP神经网络算法

BP神经网络作为当前应用最为广泛的一种多层前向反馈网络,可以实现从输入层到输出层的任意非线性映射,其结构如图1所示,其中x和y为由感知单元组成的输入层,与输入层通过权值相连的神经元h为隐含层,隐含层可以是一层或者多层,模型中每个神经元都可接收前级网络输入并将本层网络输出至后级。BP网络的前向反馈是指输入神经元经隐层神经元向输出层的正向传播过程和输出误差与预期不符时由输出层通过隐层神经元向输入层的反向传播过程实现,在整个传播过程中模型根据误差减小的方向修正输入层和隐含层之间的权值,通过正向和反向传播的迭代,权值被不断优化,输出误差与预期逐渐接近,直至收敛。

图1 BP神经网络结构图

对于GNSS高程拟合问题,输入神经元为GNSS水准点的平面坐标x和y,正向传播过程通过一组预设的初始权值wi和阈值θ将输入神经元映射到隐层神经元:

u=w1x+w2y-θ

(1)

对于包含多个隐含层的BP网络结构,通常利用Sigmoid型激活函数将当前隐含层的输入值u调整到下一隐含层的输入值:

(2)

依次计算得到每一个隐含层的输出值,直至传递到最终输出层得到输出值ς完成第一次的正向传播过程,计算当前输出值ς与期望输出值ς*之间的误差:

(3)

采用梯度下降法按照δ减小的方向调整不同层的权值w和阈值θ,并依次向输入层传递,完成第一次反向传播过程。通过上述正向传播阶段的参数选择和反向传播阶段的参数优化过程反复迭代,使BP神经网络实际输出与期望输出的差值减小至可接受范围内,即得到训练好的网络模型。

由于BP网络的求解采用的是梯度下降法,因此其性能受网络初值的选取影响较大,例如在图2所示的优化问题中,存在唯一的最小值A,如果网络初值选在a点或者b点,则根据梯度下降算法可以得到最优解,但是如果网络初始值选在c,d点和e点,则最终会陷入局部极小值B点,导致拟合性能下降。因此需要对BP神经网络初值选取方法进行优化,保证模型能够收敛于全局最优解。

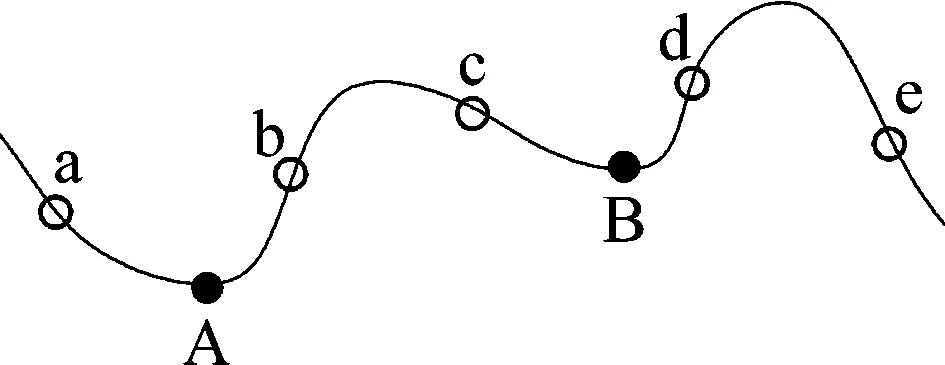
图2 存在局部极小值时优化问题示意

2 算法优化设计

2.1 GSA算法

遗传算法(Genetic Algorithm, GA)[12]和模拟退火算法(Simulated Annealing, SA)[13-14]是目前常用的两种优化算法。GA作为一种随机搜索模型,模拟的是自然界达尔文生物进化论中描述的种族的自然选择和进化过程,在算法的每一步迭代过程中,采用被称为选择,交叉和变异的操作步骤对每个种族的生物个体进行筛选,从而产生出更适合当前自然环境的种族生物集合,通过多轮的迭代更新直至最终获取最优解,GA算法具有较强的全局搜索能力,但是存在收敛速度慢,局部搜索能力较弱的缺陷。

SA算法的设计思想是模拟自然界中物质的退火过程,同样作为一种随机搜索算法,SA理论上能够以概率1收敛于全局最优解。物质退火过程中,随着温度的降低,物质的内能减少,对于任一温度,物质内都可以实现热平衡(局部最优),此时SA算法根据Metropolis准则会赋予一个跳出局部最优解的概率,从而保证其最终收敛于全局最优。SA算法具有局部搜索能力强,收敛速度快的优点,但是存在全局搜索能力差的劣势。

本文在已有研究的基础上,根据上述分析将GA与SA进行优势互补,提出一种遗传模拟退火BP(Genetic Simulated Annealing Back Propagation, GSA-BP)神经网络模型,首先利用GA对BP神经网络参数空间进行全局搜索,并将当前条件下得到的最优解作为SA的初始值,然后利用SA进行局部搜索,并将获得的满足Metropolis准则的解作为下一轮迭代中GA的初始种群,依次往复迭代,全局搜索和局部搜索交替进行,直至满足迭代终止条件,此时获得的参数即为BP神经网络模型的最优参数。

2.2 GSA-BP高程拟合算法流程

所提基于GSA-BP模型的GNSS高程拟合方法流程如图3所示,具体算法流程包含如下6个步骤:

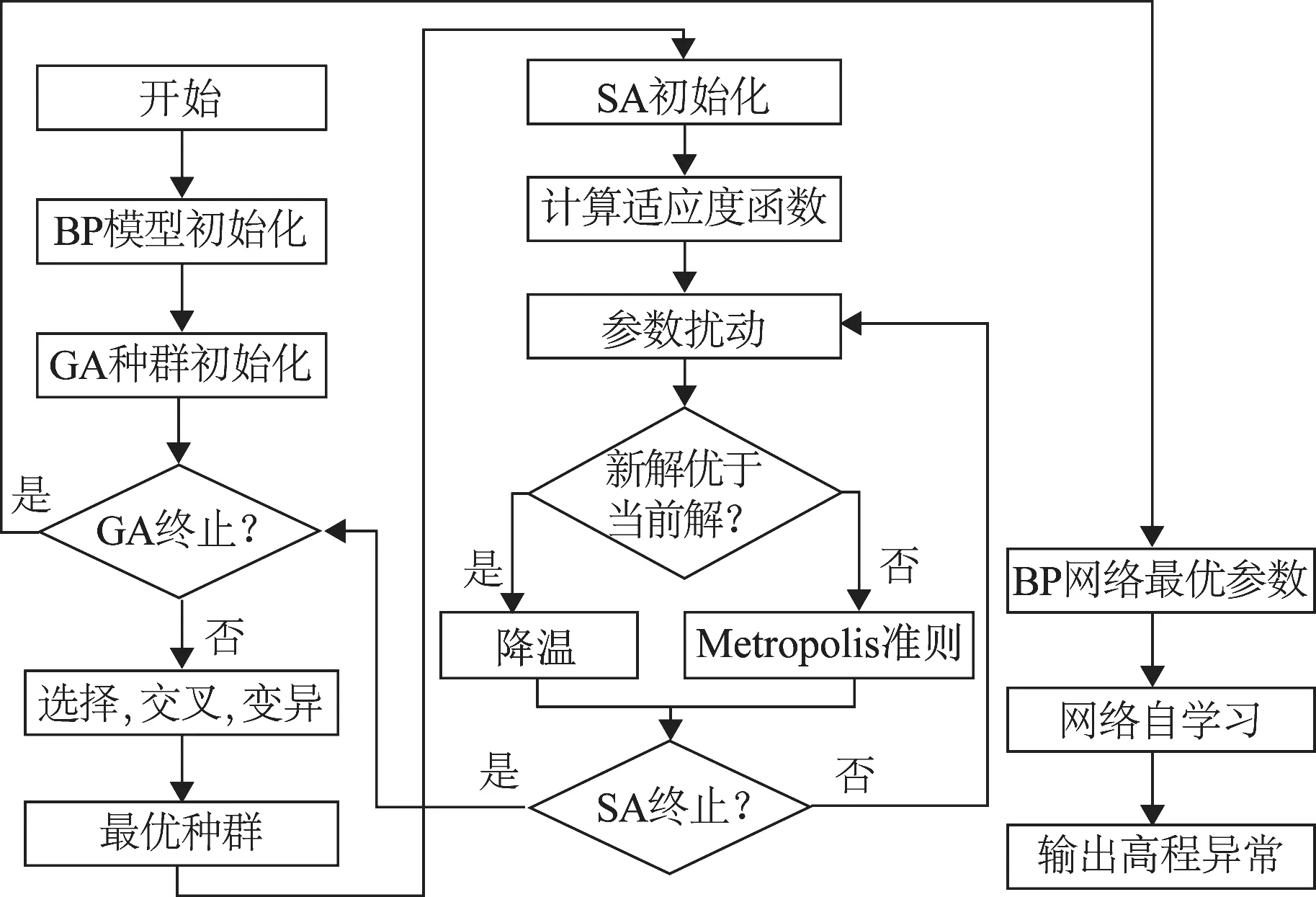
图3 GSA-BP高程拟合算法流程图

(1)BP神经网络模型初始化。对于GNSS高程拟合问题,输入神经元为GNSS水准点的平面坐标,输出GNSS水准点的高程异常,因此BP神经网络的输入神经元个数为2,输出神经元个数为1;

(2)GA模型种群初始化。将BP神经网络的初始权值w,阈值θ和隐层节点数p作为GA模型的初始种群,并对其进行编码;

(3)按如下步骤进行自适应遗传操作。

①判断当前参数下是否满足GA算法迭代终止条件,若满足则输出当前参数为BP模型的最优初始化参数w,θ和p否则转入(2);

②对当前种群进行选择、交叉和变异操作,从而得到当前的最优种群。

(4)SA模型参数初始化。将步骤3(2)中得到的最优种群作为SA模型的当前模型参数。

(5)按如下步骤进行模拟退火操作:

①计算当前初始参数对应的目标函数S;

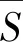
③判断当前状态是否满足SA终止条件,若不满足则进行降温,循环模拟退火操作,否则跳至步骤2,并将SA得到的新解作为GA的初始种群。

(6)GSA迭代终止后,将最优初始参数w、θ和p赋予BP神经网络进行学习,最终输出GNSS高程拟合结果。

3 实例分析

3.1 数据介绍

为了验证本文所提GSA-BP神经网络模型的GNSS高程拟合性能,采用某市D级GNSS水准控制网的实测数据开展试验,试验区域面积约98 km2,区域内均匀布设了28个四等联测GNSS水准点,图4给出了训练集和测试集点位的平面分布情况。

图4 GNSS水准点平面分布图

3.2 数据归一化

GSA-BP神经网络模型进行GNSS高程拟合时,网络模型的输入向量为GNSS水准点的平面坐标值x和y构成的二维向量,输出值为GNSS高程异常z,即网络输入层有2个神经元,输出层有1个神经元。GNSS水准点的平面坐标值与高程异常值的数值差异较大,在进行分析之前需要对数据进行归一化处理。本文采用经典的Z-score标准化方法,即利用原始的均值和标准差对数据进行归一化:

(4)

其中,p′=[x′,y′]T为归一化后的输入神经元;mean(p)为p的均值;std(p)为p的标准差。从式(4)可以看出,原始数据经过归一化后变为服从0均值,标准差为1的正态分布,完全消除了不同数据大小对结果的影响。

3.3 评价指标

为了定量的比较不同方法的拟合性能,采用如下拟合残差、残差最大值,残差最小值和残差均方根思维维度进行分析:

(1)拟合残差:

(5)

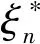
(2)残差最大值:

Δζmax=max(Δζn)

(6)

(3)残差最小值:

Δζmin=min(Δζn)

(7)

(4)残差均方根:

(8)

3.4 试验结果

根据前述分析,本文试验中BP神经网络模型输入神经元个数为2,输出神经元个数为1,GA算法的初始种群为BP网络初始参数集合P=[w,θ,p],设置其取值范围的下限和上限分别为:Pmin=[0.01, 0.01, 1]和Pmax=[100, 1, 50]。利用所提GSA算法对BP网络模型进行优化后,系统收敛时w=20.4,θ=0.37,p=6,而采用传统经验试错法对BP神经网络模型参数进行搜索得到的模型参数为w=21.3,θ=0.89,p=4。

表1给出了采用所提GSA-BP神经网络模型和传统BP神经网络模型对训练集进行拟合的结果,从表1可以看出,所提GSA-BP方法对训练集得到的最大拟合残差为36 mm,最小拟合残差为 1 mm,所有训练集的残差均方根为0.094,3项指标均小于传统BP神经网络模型(最大拟合残差174 mm,最小拟合残差9 mm,残差均方根0.291),图5给出了两种方法对训练集的拟合残差图,可以看出所提GSA-BP方法对每个样本点的拟合精度都高于传统BP神经网络,表明经GSA算法优化后获得的模型参数优于传统经验试错法获得的模型参数,即传统经验试错法获得的模型为局部最优解。

表1 不同方法对训练集的高程拟合结果 单位：m

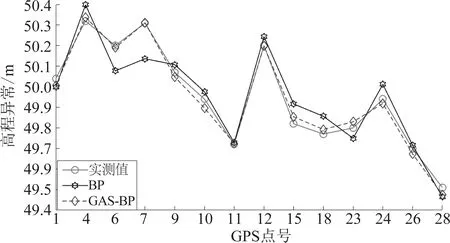
图5 不同方法得到的拟合残差(训练集)

表2给出了采用所提GSA-BP神经网络模型和传统BP神经网络模型对测试集进行拟合的结果,从表2可以看出,所提GSA-BP方法对测试集得到的最大拟合残差为43 mm,最小拟合残差为10 mm,残差均方根为0.183,而传统BP神经网络方法对测试集得到的最大拟合残差为441 mm,最小拟合残差为50 mm,残差均方根为0.706,GSA-BP方法的3项指标均优于传统BP神经网络模型。图6给出了两种方法对测试集的拟合残差图,可以看出对于每个测试样本点,GSA-BP模型的拟合精度均优于BP神经网络模型。

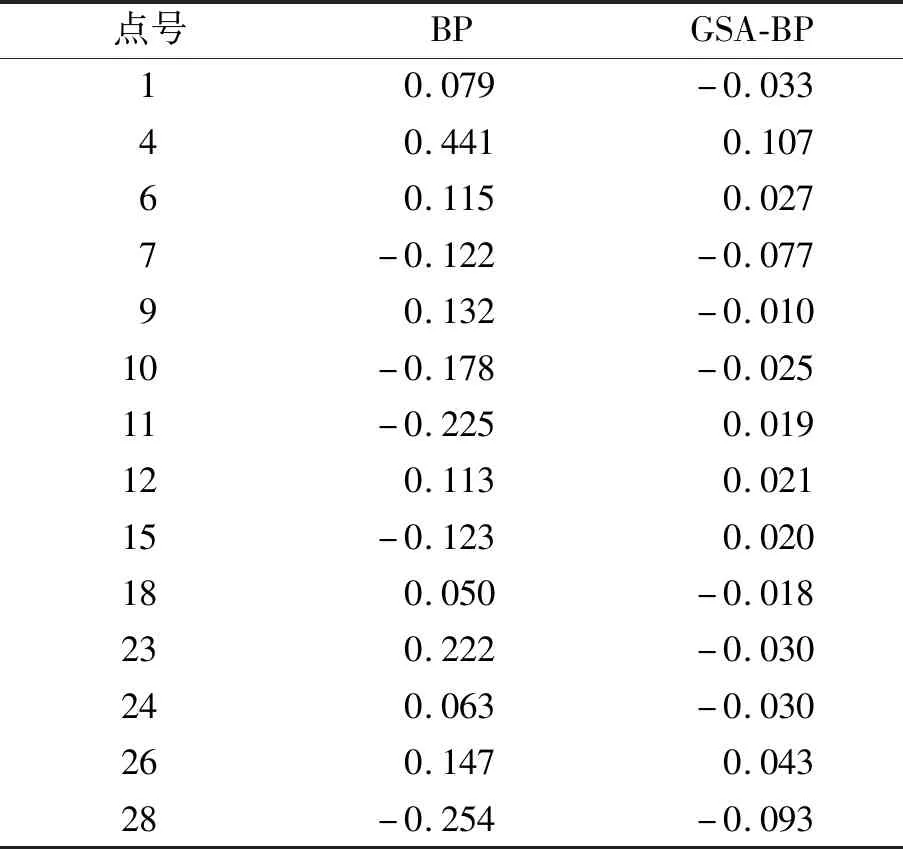
表2 不同方法对测试集的高程拟合结果 单位：m

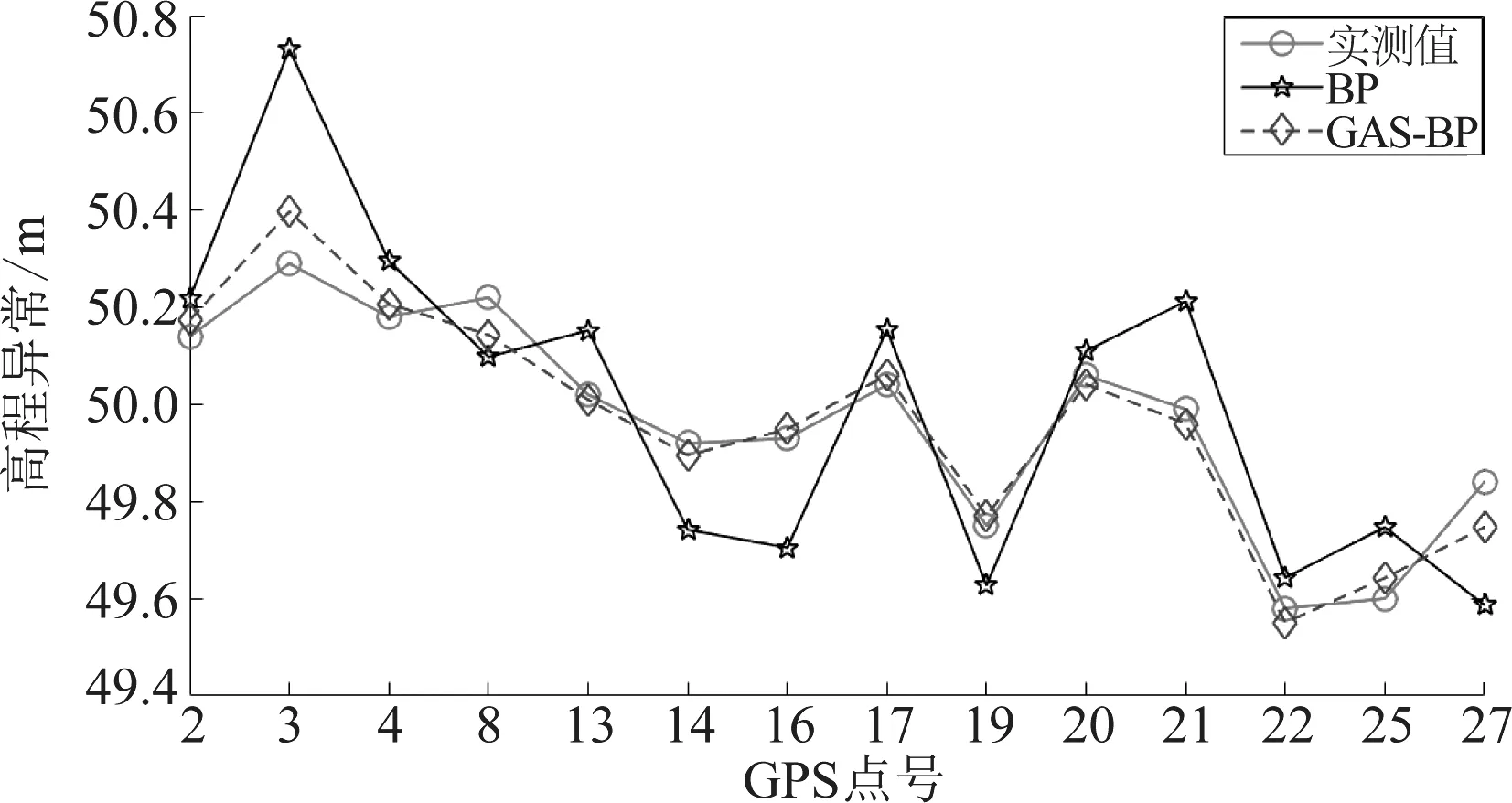
图6 不同方法得到的拟合残差(测试集)

对比训练数据集的拟合结果和测试数据集的拟合结果可以看出,GSA-BP模型获得的训练集残差均方和测试集残差均方根差值为0.089,相对于训练集残差均方根恶化了94.68%,而传统BP神经网络模型训练集残差均方根和测试集残差均方根差值为0.415,该项结果表明所提GSA-BP方法相对于传统BP模型具有更强的数据适应性和鲁棒性,更适合于工程应用。

表3给出了在相同条件下利用GSA方法和传统经验试错法对BP神经网络模型参数进行寻优所需计算时间,算法运行条件为Lenovo-Thinkpad,主频2.2 GHz的Intel 酷睿双核处理器。从表3可以看出,GSA方法由于具备更强的局部搜索和全局搜索能力,其收敛速度要快于传统经验试错法。

表3 不同方法所需计算时间 单位：s

4 结束语

GNSS高程数据得到有效利用的前提是高精度的GNSS高程拟合技术。传统基于BP神经网络模型的GNSS高程拟合方法存在拟合精度受模型参数初值选取影响较大,易陷入局部极小值的问题,本文提出一种GSA-BP神经网络模型,将GA和SA两种优化算法进行优势互补,对BP神经网络模型的权值,阈值和隐层节点数三种模型参数进行优化,确保BP神经网络能够收敛于全局最优解,最后基于某市D级GNSS水准网开展试验,从拟合残差,残差最大值,残差最小值和残差均方根4个维度对所提GSA-BP模型和传统BP模型的性能进行对比,结果表明GSA-BP模型可以获得更高的拟合精度,更强的数据适应能力,更适合于在实际工程场景中应用。

需要指出的是,本文选择的试验数据来自平原地区,地势起伏相对较为平缓,而当前丘陵,高山等地势起伏较大地区的GNSS高程拟合需求同样迫切,因此如何提升所提方法在丘陵,高山等地区的适应性和拟合精度是接下来课题组的研究方向。