提高圆形指针式仪表自动识别算法准确度的探讨

高 丽

（山西省计量科学研究院，太原 030032）

0 引言

指针式仪表由于结构简单、使用方便、安全可靠、易于维护、价格低廉等优势，被广泛应用于生产、生活等各领域[1]。在指针式仪表的校准过程中，采用图像自动识别技术可以大幅度降低校准人员的工作强度，提高劳动效率，降低人眼识别误差。但对识别精度要求较高，如果识别失败或者识别准确度不高，需要人工进行复核，反而会加重校准人员的工作负担。

由于表盘样式、背景颜色、指针数量等因素的不同，指针式仪表多种多样，但其识别流程大体是一致的。主要识别步骤有：仪表区域定位、刻度区域识别、指针检测、极坐标转换和计算识别结果等5 步，但识别过程中的细节算法对识别精度有较大的影响。为提高指针式仪表的识别准确度，本文主要针对仪表盘圆心精确定位算法、指针检测算法、指针刻度精确识别算法等细节，分别进行探讨。

图1 指针仪表识别模块流程图Fig.1 Flow chart of pointer meter identification module

1 仪表盘圆心精确定位算法

圆形表盘中，仪表刻度一般为圆弧形状，仪表指针穿过圆心。因此，刻度圆弧圆心的精确定位是决定仪表示值能否正确识别的关键，圆心定位失误会影响仪表识别的准确度，甚至造成识别失败。

对于圆形表盘圆心定位常用的方法是霍夫圆变换，霍夫圆变换是将二维图像空间中1 个圆转换为该圆半径、圆心横纵坐标所确定的三维参数空间中1 个点的过程。因此，圆周上任意3 点所确定的圆，经霍夫圆变换后在三维参数空间应对应一点。该过程类似于选举投票过程，圆周上任意3 个点为一选举人，而这3 个点所确定的圆则为一侯选人（以下称为候选圆）。遍历圆周上所有点，任意3 个点所确定的候选圆进行投票。

遍历结束后，得票数最高点（理论上圆周上任意3 点确定的圆在霍夫（Hough）变换后均对应三维参数空间中的同一点）所确定的圆即为该圆周上绝大多数点所确定的圆（以下称为当选圆）。即绝大多数点均在该当选圆的圆周上，以此确定该圆。

在图1 中可以看到，大数量的绿色的圆就是通过霍夫圆变换获得的结果。霍夫圆检测的参数调整对于结果的影响很大，检测阶段圆心的累加器阈值越大，判定条件越严苛，对于品质不高的仪表照片就可能识别失败；累加器阈值越小，检测到的圆就越多。而图1 中红色的圆弧才是刻度圆弧，圆弧的圆心与指针重合，是需要精确定位的目标，需要从众多的绿色圆中选出目标。常见方法是采用置信度和投票的方法实现这一选择，这种方法对表盘布局和图片质量要求较高，图2 中的仪表采用此方法就造成了表盘圆心定位误差。

图2 圆心定位失败的仪表Fig.2 Instrument with center positioning failure

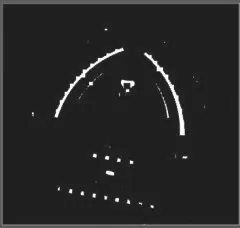
图3 仪表区域识别Fig.3 Identification of instrument area

本文设计的方法将仪表区域定位和刻度区域识别两个步骤合并，利用刻度区域为霍夫变换增加了圆心和半径的范围限制，实现表盘圆心的精确定位。这是一种形态学处理方法，根据表盘刻度区域的定位，估算对应的圆心和半径的约束范围以拟合弧形刻度线，从而完成对表盘圆心的定位。

首先，需要对仪表区域图像进行灰度化、二值化处理，然后再进行腐蚀，主要是为了删除文字和其他区域，保留刻度区域。然后，再进行膨胀操作，目的是刻度线能够连接在一起，形成最大连通域。

图3 中可以看出，最大的两个连通域就是仪表的两个表盘圆弧。使用ROI 裁剪出这两个最大连通域如图4 所示。在这一段刻度线所在的圆弧上，可以知道圆弧左右两端点A 和B 的坐标，根据圆的定理，圆心应该是在这两端点连成的线段的垂直平分线L2 上，然后通过在一定范围内枚举圆的半径，计算枚举的圆与这一区域的重叠面积，取最大重叠面积，即可估计圆弧所对应的圆心和半径。

图4 估计圆心Fig.4 Estimating the center of a circle

由于这两个数值是对图像进行膨胀处理之后的结果，可能不够精确，将其作为约束条件与霍夫圆变换结合，可实现仪表盘圆心的精确定位。

2 指针检测算法

霍夫变换还可以识别图像中的直线。欧式空间中一条直线上的点在霍夫参数空间中为一条正弦曲线；欧式空间中同一条直线上的多个点在霍夫参数空间中为1 个正弦曲线簇且曲线簇相交于一点，称此点为峰值点。而霍夫参数空间下的峰值点，则对应了欧式空间下的一条直线。 霍夫变换提取的指针直线存在着指针形状不规则，出现偏离指针线的情况。

借助精准的圆心定位，克服了指针拟合偏差问题。本文的指针检测方法是采用枚举的方式，如图6 所示。通过圆心向外延伸构造一条线段，将线段顺时针在一定夹角范围内进行旋转，旋转过程中计算线段与刻度线的相交面积比，即重叠区域像素点个数与旋转线段的像素点个数的比值，取最大值对应的线段为最终刻度线所在的线段。

图6 的仪表中有两根指针，这是一种常见情况。因此，需要先检测大指针，然后将大指针删除，再检测小指针，以防止大指针干扰小指针的识别。为避免大小指针重合的极端情况，本文设定一个针对这个指针的相交面积比值的最低阈值，在计算相交面积比值的时候，如果所有角度完成之后发现没有超过这个阈值的角度，则认为这个指针与大指针重叠了，这时候将大指针还原回去重新寻找正确的指针旋转角即可。

3 指针刻度精确识别算法

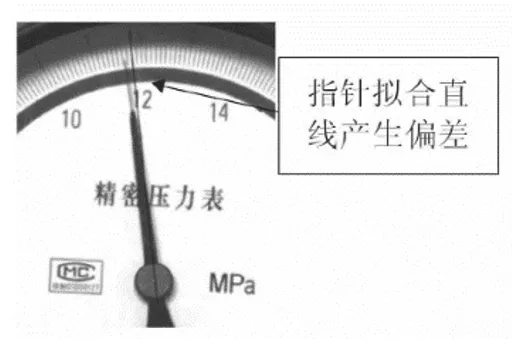
图5 箭头所指为指针拟合直线产生偏差Fig.5 The arrow indicates the deviation of the pointer fitting line

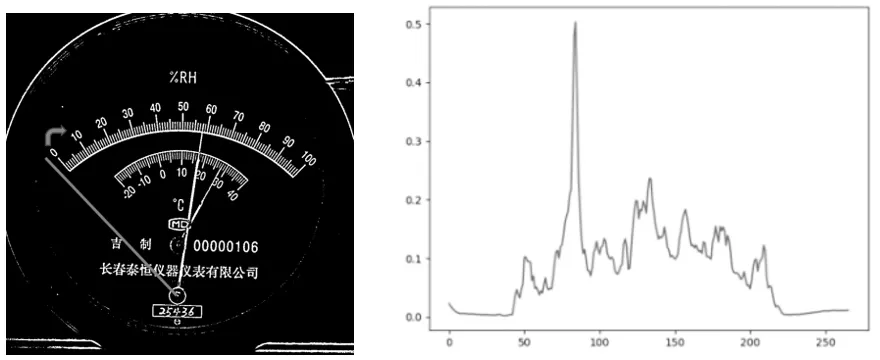
图6 指针检测过程图Fig.6 Pointer detection process diagram

在圆心和指针的精确定位之后，就可以识别指针刻度了。为了精确识别指针刻度，需要通过极坐标系转换，将仪表表盘区域进行清晰展现。将直角坐标系的圆心与极坐标系的圆心一一对应，圆弧仪表盘圆弧可以通过极坐标变换到极坐标系的一条直线上，实现由圆形到直线的转换。为提高仪表盘清晰度，本文进行了相应的处理：把刻度区域图长宽放大8 倍，由于是canny 边缘检测后的图片，所以放大对图片没有很大的影响，但是极坐标转换后的图片刻度变得很清晰。

在获得刻度区域之后，采用横向投影的方式将数字和刻度线区域分离。

实现指针式仪表图像的自动识别读数算法，按基本原理分可以归结为两大类：角度法和距离法。

施健等提出了一种指针式化工仪表的远程抄表设计方法，首先利用减影法获得指针位置，其次利用霍夫变换获得指针拟合直线的夹角，该方法受光照的影响较大。

董保同提出了一种距离法，即通过计算指针拟合直线和相邻刻度线的距离得到指针的数值，此类方法对于表盘内部无干扰因素的仪表有较好的识别效果，但对于表盘内部存在字符或其他干扰因素的情况下识别效率较低。

图7 极坐标转换效果图Fig.7 Polar coordinate conversion effect

有两种方式进行指针位置的确定，一种是采用纵向投影法之后寻找最大值坐标和两端点的坐标，另一种是纵向投影之后寻找极大值和最大值，计算最大值是在第几个极大值位置处，即可得到最后的结果。

纵向投影法，维护一个x 坐标的数组，扫描图像每一列，累积这一列中所有非0 像素点的个数，计入数组对应列的横坐标处。方法一是在统计完投影结果之后，可以记录首尾两边的横坐标x1，x2，以及上一步骤首尾的数字num1，num2，然后再记录投影数组中的最大值横坐标x0（也就是指针处的横坐标），然后根据公式（1）得到最后结果。

图8 两种结果计算方法Fig.8 Two calculation methods of results

另一个方法是在统计完投影结果之后，寻找图像中的极大值和极小值点，将极大值认为是每一根刻度线，记录下最大值处为第几根刻度线。刻度线总数N，指针在第n个刻度线处，两端点数字num1，num2，则最后结果通过公式（2）可以得到。

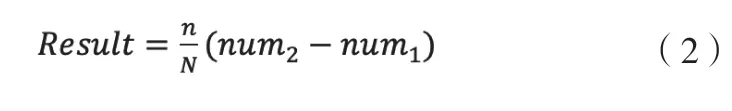
两种结果计算方法对比如图8 所示，第一种方法最后结果会精确一些。这是由于第二种方法极大值极小值的检测很容易丢失一两条刻度线，而且指针在两根刻度线中间时误差比较大。

4 结论

经过测试实验验证，以上识别算法在笔者承担的压力式温度计自动校准系统科研项目中（进行了为期半年的测试，取得数据200 组，山西省回国留学人员科研资助项目，项目编号：2016-134），识别率达到95%，对光线及角度的适应大大加强，能作为正式的算法写入识别程序中。