考虑土体非饱和特性的斜坡降雨入渗模型及边坡稳定性分析
刘卫涛,曹文贵,张运强
(湖南大学 土木工程学院,长沙 410082)
1 研究背景
滑坡灾害作为世界范围内分布最广泛、影响最严重的地质灾害之一[1-3],严重威胁着人类的生命及财产安全并对自然环境具有极大的破坏力。降雨入渗是诱发滑坡的主要因素,调查结果表明,90%以上的山体滑坡与降雨有关[4]。降雨入渗过程中土体含水量逐渐增加,土体重度增大,基质吸力减小,从而导致土体的抗剪强度降低。此外,降雨入渗是一个持续的动态过程,边坡失稳通常发生在持续降雨期间或降雨停止后的某个时间[5]。因此,有必要对降雨入渗条件下边坡的时变稳定性进行分析与研究。
降雨入渗模型结合边坡稳定性分析方法是研究降雨诱发滑坡机理的有效方法。Green-Ampt(GA)模型[6]因其具有物理意义明确、形式简单和模型参数少等优点而被多数学者广泛应用;Mein等[7]和 Chu等[8]分别以GA模型为基础将其推广应用至稳定、非稳定降雨入渗的分析当中;Chen等[9]在此基础上扩展了GA模型,并将其成功地应用到斜坡降雨入渗分析中;覃小华等[10]、汪丁建等[11]通过考虑边坡的底部边界及饱和层渗流作用,建立了考虑基岩边界的降雨入渗计算模型。然而,上述模型均假设湿润锋至入渗面间的土体为饱和状态,忽略了入渗过程中非饱和区的存在。针对这一问题,王文焰等[12]、彭振阳等[13]根据黄土和砂土入渗试验,得到了土壤含水量剖面的变化特征,据此将湿润区划分为饱和区和非饱和区,并假定非饱和区的土壤含水量剖面分布为椭圆曲线,改进了GA模型;张杰等[14]在土壤含水量分层假设的基础上,建立了降雨入渗作用下斜坡稳定性的分析方法。然而,非饱和区土壤含水量剖面分布为椭圆曲线这一假设建立在特定土壤入渗试验的基础之上,不具有普适性。之后,李宁等[15]基于非饱和土的特性,提出了低强度长时和高强度短时降雨作用下无限斜坡稳定性的简化计算模型,但未考虑湿润区含水量随深度变化这一客观事实。张丁等[16]基于达西定律建立了湿润区含水量沿深度变化的积水入渗模型,但未考虑斜坡降雨入渗的情况。
基于上述研究的不足,本文在改进的GA入渗模型和非饱和土Van Genuchten(VG)模型[17]基础上,建立考虑湿润区含水量沿深度变化的斜坡降雨入渗模型,并结合无限斜坡模型分析了斜坡的稳定性,推求出斜坡稳定性系数随降雨时间的变化规律。
2 Green-Ampt模型及其改进模型
Green-Ampt(GA)模型是描述非饱和土中水分瞬时入渗的经典模型,该模型通过干燥土柱的积水入渗试验,直接采用达西定律求解土壤水分入渗速率,很好地描述了薄层积水条件下水分的入渗过程。因其阶梯状湿润锋锋面,所以又被称为活塞入渗模型。该模型的基本假定是:①土体表面至湿润锋锋面之间的水分均匀连续分布;②湿润区含水量为饱和含水量θs,干土层含水量为初始含水量θi。图1为GA模型入渗简图。
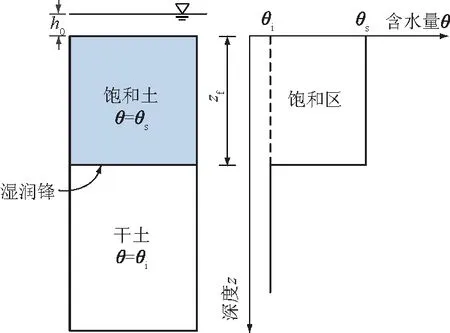
图1 GA模型入渗简图Fig.1 Infiltration diagram of Green-Ampt model
基于上述基本假定,根据质量守恒定律,GA入渗模型可以表示为
(1)
式中:i为入渗速率;I为累积入渗量;t为入渗时间;Ks为饱和渗透系数;zf为湿润锋深度;h0为地表积水深度;hf为湿润锋平均基质吸力水头。
GA模型假设入渗过程为饱和入渗,故累积入渗量与湿润锋深度的关系可以表述为
I=(θs-θi)zf。
(2)
由式(1)、式(2)的导数关系,可得湿润锋深度随时间的发展规律为
Chen等[9]考虑地表的倾角对稳定和非稳定入渗的影响,对GA模型进行了修正。当降雨强度大于土体的入渗能力时,垂直于坡面方向的入渗速率可表示为
(4)
式中β为斜坡表面倾角。
GA模型和改进的斜坡GA模型均假设湿润区含水量为饱和含水量,然而在入渗过程中土体很难达到完全饱和状态,尤其在斜坡降雨入渗的过程中,由于沿坡面的渗流作用,坡表以下土体往往处于非饱和状态。上述饱和入渗模型忽略了非饱和区的存在,这显然与实际不相符。因此,有必要探究降雨入渗过程中湿润区含水量沿深度变化的真实情况。
3 基于土水特性的斜坡降雨入渗模型
3.1 斜坡内湿润区土体基质吸力分布
由土-水特征曲线(SWCC)可知,土体含水量的大小主要取决于土体基质吸力的大小,降雨入渗的过程本质上是土体吸湿的过程。因而,为获得降雨入渗过程中湿润区土体含水量的真实分布,应首先分析降雨入渗过程中基质吸力的分布情况。
图2为斜坡降雨入渗的计算简图,选取垂直坡面向下方向为正方向,为得到湿润区基质吸力的变化规律,在坡面、湿润区及湿润锋上选取A、B、C为计算点。土体水分运动的驱动力主要由某一位置土体水势与标准参考状态的势能差决定,土体水总势能可表示为
ψ=ψg+ψp+ψm。
(5)
式中:ψ为土体水总势能;ψg为重力势能;ψp为压力势能;ψm为基质势能。
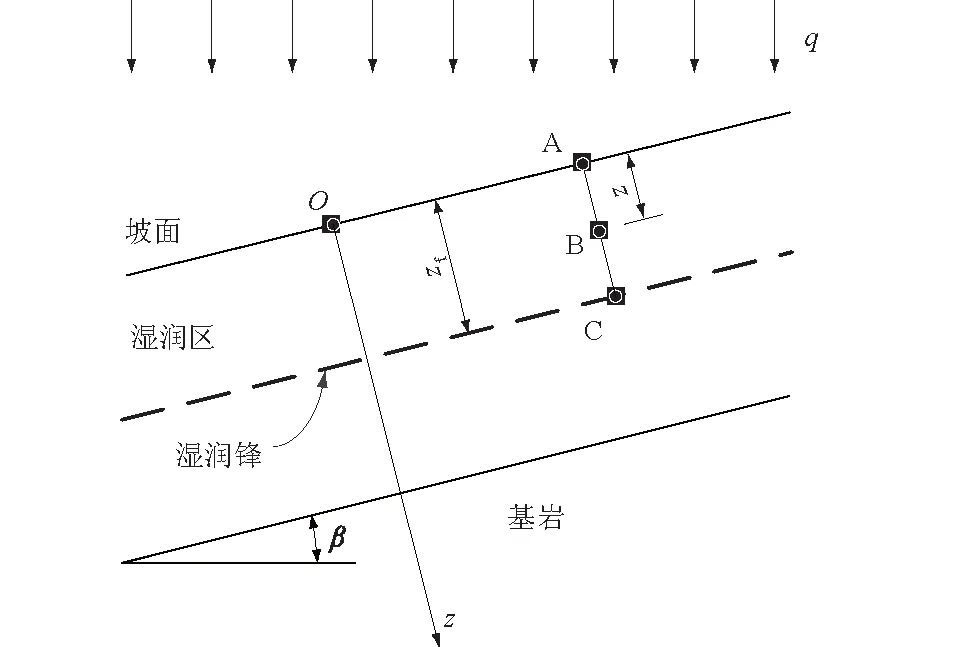
图2 斜坡降雨入渗简图Fig.2 Sketch of rainfall infiltration in slope
根据式(5)分别计算A、B、C三点的总势能:
ψA=0 ;
(6)
ψB=zcosβ+hB;
(7)
ψC=zfcosβ+hf。
(8)
式中:z为B点至坡面的垂直距离;hB为斜坡内B点的基质吸力水头。
假设降雨入渗过程中土体水分流动满足达西定律,即
(9)
式中K(θ)为非饱和渗透系数。
采用式(9)的差分形式,由A、B两点的势能差,可得坡面入渗速率为
(10)
同理,根据A、C两点可得
(11)
由式(10)、式(11)相等,可得湿润区任意深度处的基质吸力h(z)为
(12)
3.2 斜坡内湿润区土体含水量分布
由式(12)可知湿润区土体任意深度处基质吸力,进而可以根据土水力学特性得到湿润区土体含水量的分布。土体含水量和基质吸力的关系可以由SWCC进行定量计算。VG模型[17]是一个三参数的平滑封闭数学模型,与其他模型相比,因其对不同土体具有良好的适应性而被广泛使用。VG模型[17]的具体表达式为
(13)
式中:θs为土体饱和体积含水量;θr为土体残余体积含水量;h为土体基质吸力;α、n、m均为拟合参数。
将式(12)代入式(13),可以得到湿润区任意深度处土体含水量θ(z)为
(14)
与GA模型及其改进模型相比,式(14)考虑了不同土体的水力学特性,更加真实地描述了降雨入渗过程中土体含水量的分布规律。

图3 土体剖面含水量分布Fig.3 Water contentdistribution in soil profile
3.3 斜坡降雨入渗模型
降雨的累计入渗量I可用式(15)计算,即
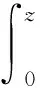
(15)
将式(14)代入式(15)得
I=(θr-θi)zf+
(16)
式(16)右边第二项为不定积分算式,为便于求解和后面的分析,对式(16)进行简化计算。
根据式(14),可得斜坡内剖面含水量沿深度变化的分布,如图3所示。参考文献[13]和文献[16]的简化方法,基于剖面含水量的分布形状将其简化为I和J的组合,以湿润锋含水量θzf为界,I、J分别假设为矩形和1/4椭圆。
将z=zf代入式(14),可得湿润锋含水量θzf为
(17)
根据简化后剖面含水量的形状,任意深度处土体含水量θ(z)可简化为
将式(18)代入式(15)得累积入渗量I为
(19)
对式(19)求导可得入渗速率,即
(20)
Mein等[7]认为随着降雨的持续进行,降雨入渗的边界条件会发生转变,这主要由降雨强度和土体入渗能力控制。降雨初期,入渗过程由降雨强度控制,这个阶段降雨强度小于土体的入渗能力,雨水全部进入坡体内。假设恒定降雨强度为q,考虑坡角的影响,垂直于坡面方向的入渗速率为
i=qcosβ。
(21)
随着降雨的持续入渗,坡表土体趋于饱和,土体的入渗能力逐渐减小,当土体的入渗能力小于降雨强度时,入渗边界条件转为由土体入渗能力控制阶段。根据文献[9]中改进的GA模型,不考虑坡面积水,垂直于坡面方向的入渗速率可表示为
(22)
根据降雨入渗速率的连续变化,存在临界时刻tp,对应入渗深度为zp,此时降雨强度在坡面方向的分量等于土体的入渗能力,使得
(23)
整理得
(24)
将式(24)代入式(19)得临界累积入渗量为
(25)
由式(25)、式(21)的导数关系,得
当降雨强度小于土体的入渗能力时,即t≤tp时,由式(20)、式(21)可得
整理得
(28)
当降雨强度大于土体的入渗能力时,即t>tp时,由式(20)、式(22)可得
(29)
整理得
(30)
综上所述,降雨入渗全过程中,湿润锋深度的发展速率与降雨时间的关系为
(31)
对式(31)进行积分,并代入初始边界条件t=0,zf=0;入渗临界条件t=tp,zf=zp,得
(32)
式(32)反映了降雨入渗过程中湿润锋深度的动态变化规律,相比于式(4)改进的GA模型,本文模型考虑了降雨入渗过程中湿润区含水量沿深度的变化,更加符合实际。
4 无限斜坡稳定性分析
本节主要基于上节得到的湿润锋深度随降雨时间的变化,分析降雨过程中天然边坡的稳定性变化规律。降雨诱发的滑坡往往平行于斜坡表面,且滑动面通常较浅(最多数米),并且滑动面往往在湿润锋处[18]。此外,滑坡的长度通常远大于滑动面的深度,这种情况下,可以忽略斜坡上、下的边界效应,采用无限斜坡模型对天然边坡进行简化,如图4所示。下面将以湿润锋处为潜在滑面进行稳定性分析,推导降雨条件下无限斜坡的时变稳定性。
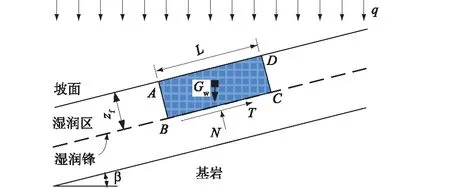
图4 降雨条件下无限斜坡的稳定性分析示意图Fig.4 Schematic diagram of stability analysis ofinfinite slope under rainfall
如图4所示,取一代表性土体条块ABCD进行受力分析。降雨入渗过程中土体为变饱和状态,土体重度随含水量的变化而变化,任意深度土体的重度为
(33)
式中:γ(z)为湿润区深度z处的土体重度;γd为土体的干重度;γi为土体初始重度。
将式(18)代入式(33),得
(34)
式(34)反映了降雨条件下土体重度沿深度变化的规律。
结合式(34),代表性条块ABCD的质量Gw为
(35)
式中L为代表性条块的长度。
以L×1面积进行分析,由力学平衡方程可得滑动面剪应力τs和正应力σ为:
变饱和条件下,基于Lu等[19]的非饱和土统一有效应力原理,得
σ′=σ-ua-σs=
式中:ua为孔隙气压力;σs为吸应力,与土体的含水量及基质吸力相关。
式(38)中σs为
式中:σ′为有效应力;uw为孔隙水压力。
滑动面的抗剪强度可由Mohr-Coulomb破坏准则得到,即
τf=c′+σ′tanφ′=c′+
(40)
式中:τf为抗剪强度;c′为有效黏聚力;φ′为有效内摩擦角。
在极限平衡状态下,斜坡的稳定性系数FS定义为滑动面抗剪强度τf与剪应力τs的比值,即
(41)
将式(36)、式(40)代入式(41)可得
(42)
联立式(32)和式(42)即可得到恒定降雨强度q下,斜坡的稳定性系数随降雨历时的动态变化规律。
在实际工程中,已知降雨强度和土体的基本参数时,根据相关规范FS取最小稳定性系数,由式(42)可以计算得到斜坡失稳时的临界湿润锋深度(即滑动面位置),将临界湿润锋深度代入式(32)中可以反算斜坡失稳的时间,将有助于预测降雨过程中斜坡失稳破坏的发生。
5 模型验证与参数分析
为验证本文提出的斜坡降雨入渗模型及斜坡稳定性分析的正确性,选用文献[15]的数值解进行验证,并与文献[15]的计算方法以及Mein-Larson方法[7]进行对比。文献[15]给出了降雨强度q=4.333×10-4m/min、斜坡倾角β=30°,降雨时间为6、7、8、9、10 h的数值解。具体土体参数如表1所示。

表1 土体的基本参数Table 1 Basic parameters of soil
5.1 斜坡降雨入渗模型验证
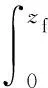
图5为恒定降雨强度下采用本文方法、文献[15]的计算方法及Mein-Larson方法得到的入渗过程中湿润锋深度随降雨时间的变化规律。
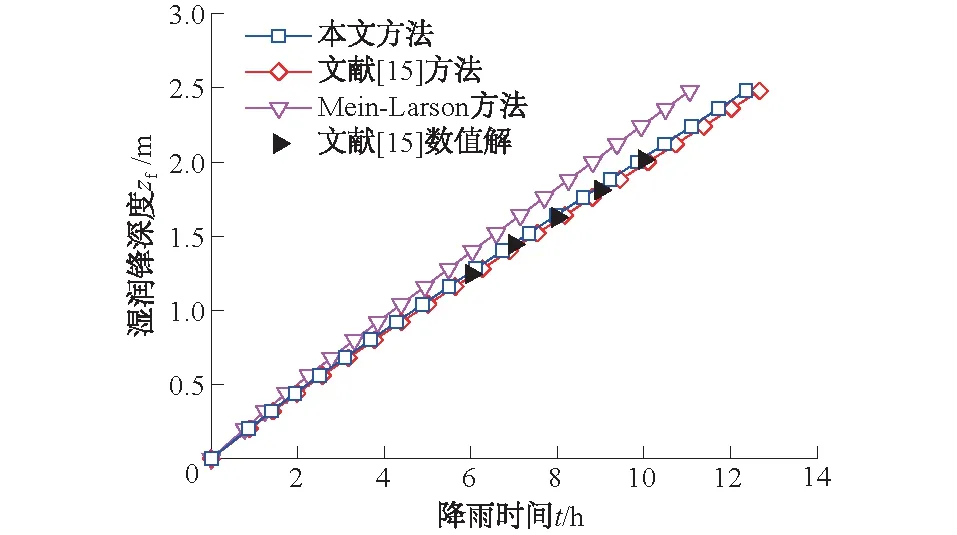
图5 不同模型湿润锋深度随降雨时间的变化Fig.5 Variation of wet front depth with rainfallduration in different models
由图5可知,降雨入渗初期,入渗边界条件由降雨强度控制,湿润锋深度随降雨时间线性增加。降雨中后期土体的入渗边界转为由土体的入渗能力控制,入渗速率逐渐减小并最终趋于稳定,湿润锋深度随降雨时间呈现一定程度的非线性。通过与数值解对比发现,相较于Mein-Larson模型,本文模型与文献[15]的模型能较好地模拟降雨入渗后期湿润锋深度随时间的变化规律,并且本文模型的计算结果更加接近数值解,从而验证了本文降雨入渗模型的正确性。此外,分析三者模型可知,本文模型与文献[15]模型计算结果相差不大,主要由于验证文献中土体的初始含水量较大,土体在短时间内很快趋于饱和,这时两者模型趋于一致。然而,对于初始含水量较小的土体,降雨入渗过程中土体的含水量变化较大,文献[15]模型虽然考虑了土体的非饱和特性,但未考虑含水量沿深度的变化,将不再适用。Mein-Larson模型认为降雨初期雨水全部进入土体,忽略了沿坡面的渗流,所以相同时间下,湿润锋深度计算结果偏大。
5.2 斜坡稳定性分析方法验证
图6为采用上述3种模型计算的稳定性系数随降雨历时的变化规律。通过与数值解对比发现,本文模型的计算结果与数值解吻合较好,很好地反映了降雨入渗过程中斜坡稳定性的变化,从而验证了本文斜坡稳定性分析方法的正确性。
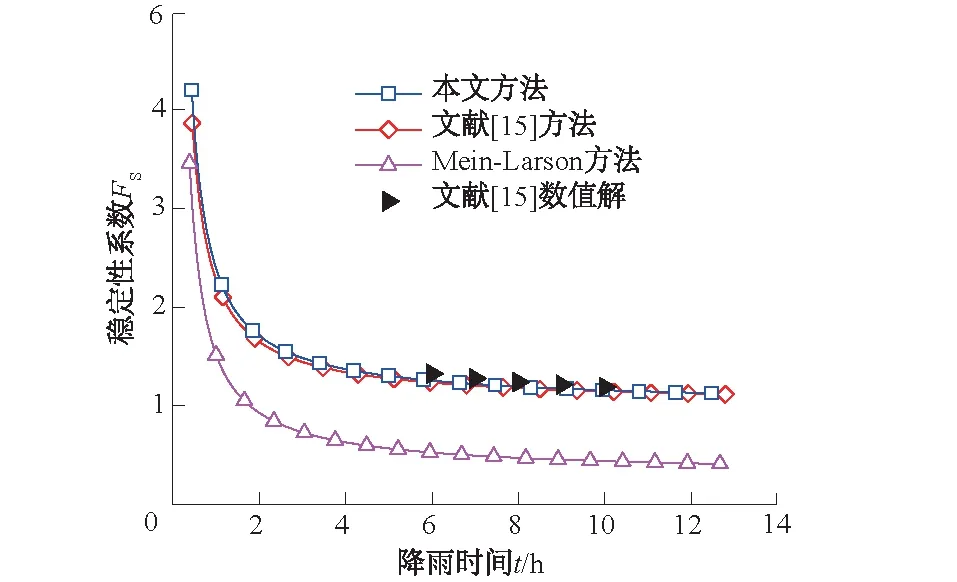
图6 不同模型稳定性系数随降雨时间的变化Fig.6 Variation of stability coefficients of different models against rainfall duration
此外,由图6可知,3种模型计算的稳定性系数随时间的变化呈现一致的规律性,降雨初期3种模型计算的稳定性系数均随降雨时间迅速下降,并且在降雨后期3种模型计算的稳定性系数下降速率均减缓。同一降雨历时下,本文模型计算的稳定性系数最大,其次是文献[15]模型,Mein-Larson模型的计算值最小。这是因为本文模型考虑了入渗过程中非饱和区的存在,进而考虑了基质吸力的作用;而Mein-Larson模型认为湿润区土体处于饱和状态。由上可知相同工况下,传统的饱和入渗模型计算的稳定性系数过于保守。
为了进一步对比考虑湿润锋面上方非饱和区存在对斜坡稳定性系数FS计算结果的影响,选取文献[15]的土体参数,设置斜坡角度为50°,分别采用本文模型和改进的GA模型计算斜坡的稳定系数FS。图7为该工况下斜坡稳定性系数随湿润锋深度和降雨时间的变化关系。
图7 斜坡稳定性系数随湿润锋深度和降雨时间的变化Fig.7 Variation of slope stability coefficient withwetting front depth and rainfall duration
由图7可知:本文模型计算的稳定性系数高于GA模型的计算结果,曲线显示所取工况下湿润锋到达0.19 m(即降雨时间为0.72 h)时,GA模型的计算结果显示斜坡已经达到失稳状态,然而考虑湿润锋锋面上方非饱和区存在时所计算的稳定系数认为斜坡仍处于安全状态,降雨直至湿润锋发展至0.41 m(即降雨时间为2.41 h)时斜坡失稳。GA模型计算的失稳深度小于本文模型的计算值,而且失稳时间较本文模型提前,因此忽略湿润锋上方非饱和区的存在会大大降低斜坡的稳定性系数,这与文献[14]的结论相一致。
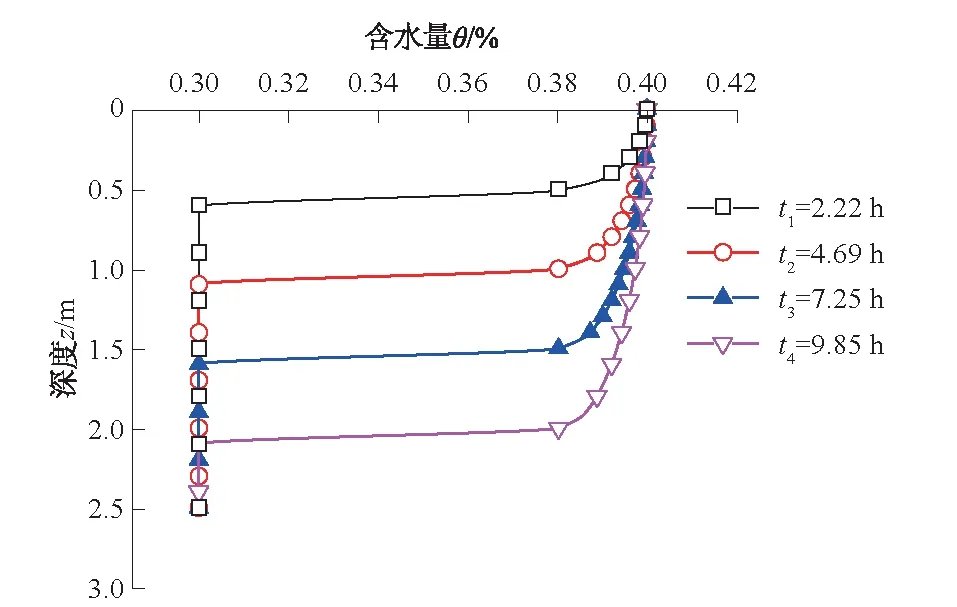
图8 土体剖面含水量随降雨时间的变化Fig.8 Variation of water content of soil profile againstrainfall duration
5.3 参数分析
5.3.1 不同降雨时间下土体剖面含水量的分布
图8为不同降雨时间下土体剖面含水量的分布,随着降雨的进行,水分不断向下入渗,湿润锋上方土体含水量逐渐增大,并逐渐趋于饱和。降雨时间t为2.22、4.69、7.25、9.85 h时,湿润锋深度分别为0.5、1.0、1.5、2.0 m。湿润锋深度增量为0.5 m,入渗时间间隔分别为2.22、2.47、2.56、2.60 h。由此可知,随着时间的推移,湿润锋锋面不断向下发展,但其扩展速率逐渐减小。
5.3.2 不同降雨强度影响
选取与文献[15]相同的土体参数及斜坡数据,研究不同降雨强度下,湿润锋深度及稳定性系数的动态变化规律。降雨强度分别控制为3×10-4、3.47×10-4m/min(达到土体饱和渗透系数)、4×10-4、5×10-4m/min及6×10-4m/min。图9为不同降雨强度下湿润锋深度和斜坡稳定性随降雨时间的变化规律。
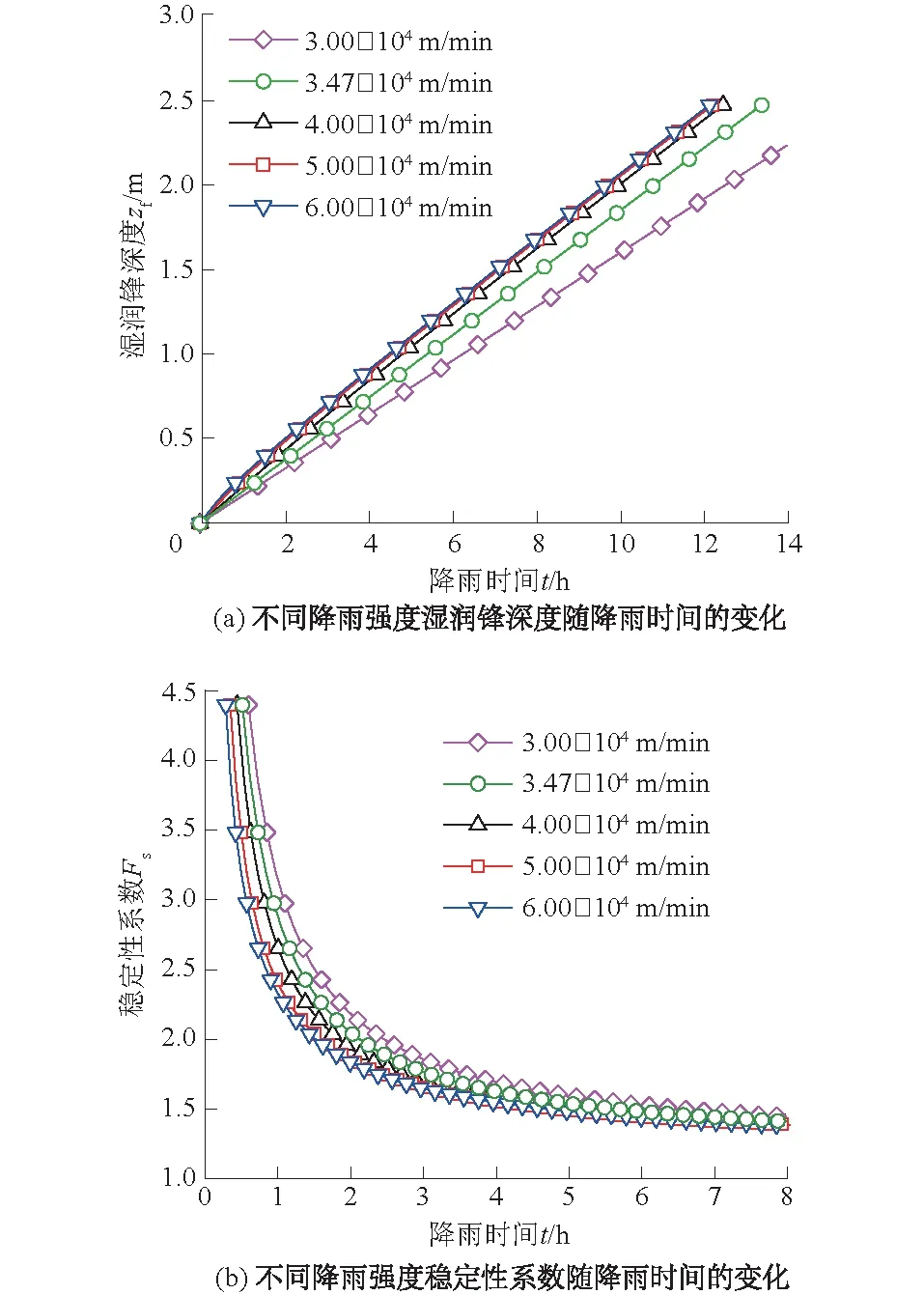
图9 不同降雨强度湿润锋深度和稳定性系数随降雨时间的变化Fig.9 Variations of stability coefficient and wet frontdepth against rainfall duration under different rainfallintensities
由图9(a)可知,当降雨强度不超过土体的饱和渗透系数时,湿润锋深度随降雨时间线性增加。当降雨强度大于土体的饱和渗透系数时,由于入渗边界条件的变化,湿润锋深度随降雨时间呈现一定程度的非线性。随着降雨强度的增大,相同时间内湿润锋深度的变化速率减缓。当降雨强度增大到某一值时,入渗边界在很短时间内转为由土体入渗能力控制,降雨强度控制阶段可以忽略不计,此时可以认为降雨强度继续增大对湿润锋深度的发展规律基本不再产生影响。如图9(b)所示,可以看到在降雨初期,随着降雨强度的增加,斜坡稳定性系数逐渐减小,并且在降雨后期趋于一致。此外,降雨强度达到某一值时,稳定性系数不再发生显著变化。
5.3.3 不同斜坡角度影响
为了研究不同斜坡角度对湿润锋深度和斜坡稳定性随降雨时间的变化规律,分别取斜坡倾角为20°、30°、40°和50°进行研究。图10(a)和图10(b)分别为不同坡角下湿润锋深度和斜坡稳定性随降雨时间的变化规律。

图10 不同坡角湿润锋深度和稳定性系数随降雨时间的变化Fig.10 Variations of stability coefficient and wetfront depth against rainfall duration in the presence ofdifferent slope angles
由图10(a)可知,随着坡角的增大,湿润锋深度随着坡角的增大而减小,这是由于坡角增大时雨水沿坡面方向的渗流增加,垂直于坡面方向的渗流减小,导致降雨强度控制阶段时间延长。由图10(b)可知,斜坡稳定性系数亦随坡角的增大而减小,并且相同坡角增量下稳定性系数的降低速率减缓。事实上,从式(42)可以看出,当土体参数确定时,斜坡的稳定性系数仅取决于湿润锋的深度和坡角,而坡角的增大同时会降低湿润锋深度和斜坡稳定性,这表明在降雨入渗的全过程中坡角对斜坡的稳定性有着更为显著的影响。
6 结 论
本文基于达西定律和非饱和土VG模型,得到了降雨入渗过程中土体剖面含水量的分布规律,结合改进的GA入渗模型,推导得到了考虑斜坡湿润区含水量随深度变化的降雨入渗模型,并将其应用到降雨条件下无限斜坡的稳定性分析中,得到以下结论:
(1)通过与数值解对比,验证了本文模型在求解湿润锋深度发展规律及斜坡时变稳定性系数方面的正确性与适用性。
(2)随着降雨的持续进行,湿润锋不断向下发展,但湿润锋的发展速率逐渐减小。斜坡的稳定性系数随降雨时间的增长不断减小,降雨初期迅速下降,降雨后期下降速率逐渐减缓。
(3)随着降雨强度的增大,相同时间内湿润锋的深度逐渐增大,斜坡稳定性系数逐渐减小,但湿润锋深度的增大速率和稳定性系数的下降速率逐渐减缓。当降雨强度增大到某一值时,降雨强度继续增大对湿润锋深度和稳定性系数的发展规律基本不再产生影响。
(4)随坡角的增大,相同时间湿润锋深度和斜坡稳定性系数同时减小,并且相同坡角增量下稳定性系数的降低速率逐渐减缓。这表明坡角的大小对斜坡的稳定性有着更为显著的影响。
本文在分析斜坡稳定性时,采用无限斜坡模型,未考虑斜坡表面和滑动面不是平直的情况,将在以后作进一步分析。

