基于不同等效方法的储罐内爆载荷计算与结构破坏分析

丁宇奇 叶碧涛 芦 烨 成佳浩 卢 宏 谢 清 王学勇

（东北石油大学机械科学与工程学院）

随着石化工业的发展，近年来能源危机不断加大，国家原油战略储备库项目的实施迫使我国不得不建造更多更大的储罐。 储罐储存的液体或者气体多为易燃易爆物品，容易发生爆炸事故［1～3］。 为了减小爆炸事故造成的伤害，需要对储罐内爆载荷与储罐结构破坏之间的关系进行研究。

目前， 针对爆炸载荷计算方法的研究有很多。在理论计算方面，最常见的方法是以TNT炸药为计算标准，将气云爆热等效为TNT当量来计算，即TNT当量法［4］。张丽运用TNT当量法计算了不同燃气性质、不同泄漏量以及不同泄漏口径等情况下燃气泄漏爆炸产生的冲击波值，并预测了可能对结构产生的破坏［5］。 丁宇奇等依据TNT当量法推导出了储罐内爆超压分布曲线，得到了不同起爆点和不同液位会影响储罐破坏位置的结论［6］。然而， 由于爆炸时的物理和化学过程相当复杂，致使理论求解范围极其有限，且理论计算无法观测到破口的形貌。 而数值模拟在获得爆炸过程中各种动态物理量的同时，还可以得到更加全面且足够精确的计算结果，因此得到了广泛的应用［7，8］。常用的确定容器内爆载荷的数值模拟方法主要有两种：计算流体动力学（CFD）方法和TNT当量法，已有不少学者对两种方法进行了对比研究。 张秀华等建立了相同装药形状的乙炔气团和当量的TNT两种爆炸源模型， 在分析两种爆源产生的超压曲线后， 得到了随着距爆源距离的增加，两种爆炸压力波形间的误差逐渐减小的结论［9］。但是，这种方法是单纯的将乙炔浓缩为高能爆炸气团，没有考虑乙炔与空气的化学反应。 为此， 芦烨等考虑可燃气云爆炸时的化学反应，分别采用TNT当量法和CFD方法研究了二维储罐模型内的压力和速度变化，研究结果表明：CFD方法能更好地描述储罐内的压力场分布［10］。 然而，该研究仅分析了罐内流场，没有对爆炸载荷作用下储罐结构破坏进行研究。 实验方法可以直接有效地获取结构破坏研究所需的数据，姚术健等通过多次箱型结构内爆实验，得出了箱体在内爆作用下会出现板中心冲切破口、箱体角隅处破坏及板边缘撕裂等多种破坏形式的结论［11］。Vanessa P等开展了金属容器内爆实验，分别使用金相分析和高速摄像技术对结构破坏进行了分析，指出结构破坏是由焊接热影响区域应变过大和材料强度降低导致的［12］。 然而，进行爆炸实验研究的成本非常高，同时实验过程存在一定的危险性。

综上所述，数值模拟方法是开展爆炸载荷研究的最佳方法，但是目前鲜有人针对储罐在不同载荷等效方法下的结构破坏进行数值模拟研究。因此，笔者以立式拱顶储罐为研究对象，考虑储罐角钢结构和壁板变壁厚的特性， 分别使用CFD方法和TNT当量法对储罐结构破坏进行数值计算。 通过分析储罐结构的应力、变形和破坏位置，得到两种方法在不同容量储罐和不同爆心距下的储罐破坏形貌， 为研究储罐内可燃气云爆炸时，两种等效方法在载荷计算和结构破坏时的误差范围提供参考。

1 储罐内可燃气云爆炸载荷不同等效方法分析及模型建立

1.1 储罐内可燃气云爆炸载荷CFD方法及模型建立

可燃气云爆炸是一种带有剧烈化学反应的过程，表现出来的形态为逐层燃烧，火焰从点火点逐步扩散，火焰在扩散过程中加速并形成爆轰波。 爆轰波的传播速度为每秒数千米，燃烧过程伴有强烈的压力升高［13］。 笔者在使用CFD方法模拟储罐爆轰过程时不考虑温度作用和气体的泄漏， 此时储罐内的爆炸压力可视为定容爆炸压力。 气体定容爆炸压力pm与初始环境压力p0有以下关系［14］：

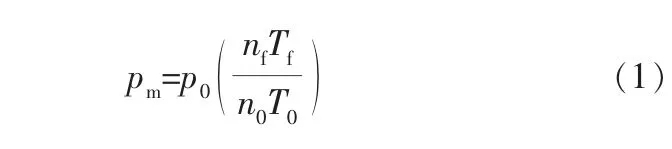
其中，n0为气体初始摩尔量；T0为反应初始温度；nf为反应终态摩尔量；Tf为反应终态温度。为了使储罐内可燃气云燃烧发展成爆轰波，以达到储罐爆炸破坏效果，笔者采用设置高温点火源的方法驱动爆轰波形成。 为简化计算，将储罐内部可燃混合气体视为理想气体，混合气体满足理想气体状态方程。 使用Fluent流体仿真软件来模拟可燃气体燃烧爆炸过程。 在保证较好模拟湍流扩散燃烧反应的前提下， 采用计算量较小的EDC燃烧模型，同时使用k-ε湍流模型实现燃烧时的湍流流动［15］。

笔者分析的储罐容积为3 000、5 000、10 000m3，三者直径分别为15、20、27.5m，罐壁高均为17.82m，罐顶曲率半径为直径的1.2倍，壁板厚度由上到下逐渐增大。 可燃气体点火点的位置选择在储罐1/2高度，距离罐壁5m（N1）、3m（N2）、1m（N3）处。并选择最先接触爆炸波位置设置测点A， 另外在罐顶与罐壁连接处位置设置测点B、C。因为该位置结构不连续， 同时厚度也是最薄弱的。限于篇幅，本节仅以5 000m3储罐做详细分析。根据5 000m3罐尺寸在Fluent中设置储罐内可燃气体域。在初始化设置上，混合气体初始温度300K，并在点火位置设置一个2 500K的高温区域以及少许反应产物。 可燃气体浓度取乙炔反应最剧烈的浓度7.4%，5 000m3储罐流体域有限元模型如图1所示。

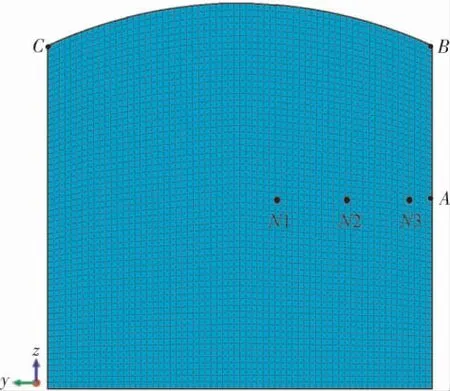
图1 CFD分析储罐有限元模型

1.2 储罐内可燃气云爆炸载荷TNT当量法及模型建立

由于可燃气云爆炸的复杂性，通常将可燃气云爆炸的能量等效成当量的TNT来研究爆炸对结构的破坏［16］。使用TNT当量法模拟储罐内爆时，巨大的爆炸能量会在瞬间全部释放，产生大量的高温高压爆炸产物，急剧膨胀的爆炸产物会压缩周围的空气并使之偏离原有位置，形成一层高压空气波。 随着爆炸气体的继续膨胀，其体积的增大带来的后果就是压力的不断减小，最终爆炸波压力将与大气压相同。TNT爆炸压力p的计算一般使用JWL状态方程［17］：

其中，V为爆轰产物相对比容；E为爆轰产物的比内能；A、B、R1、R2、ω均为JWL方程参数。 爆炸威力取决于可燃气体换算的TNT当量，TNT当量计算公式如下：

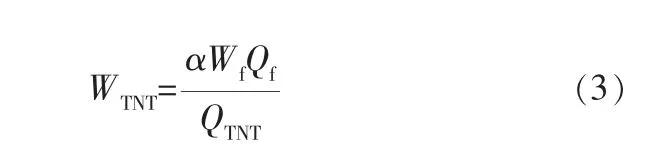
其中，WTNT为可燃气体的TNT当量；α为可燃气体的效率因子，表明参与爆炸的可燃气体的体积分数，其中乙炔的效率因子为19%；Wf为可燃气体的总质量；Qf为可燃气体的燃烧热；QTNT为TNT的爆炸热，一般取4.61×103kJ/kg。 将3 000、5 000、10 000m3储罐内可燃气体换算后， 得到TNT当量分别为276、498、962kg。

与CFD方法中流体域位于结构模型内部不同，TNT当量法采用CEL方法计算，因此建立的流体域要大于结构模型，以保证结构发生变形破坏后数据能继续传递。 为了得到较好的网格质量，使用VOF法指派TNT为球形装药并设置初始空气体积分数， 得到TNT当量法分析储罐有限元模型如图2所示。

图2 TNT当量法分析储罐有限元模型

2 不同等效方法下的储罐内爆载荷计算

2.1 CFD方法计算储罐内可燃气云爆炸载荷

由于笔者采用的CFD方法无法模拟储罐破坏后罐内压力的泄放， 因此在使用CFD方法计算储罐内可燃气云爆炸载荷时，仅提取爆炸破坏前测点的压力。 限于篇幅，本节仅提取5 000m3储罐中N2点火点的工况数据。爆炸波刚接触到罐壁时的压力分布如图3所示，A、B、C点的压力随时间变化曲线如图4所示。

图3 CFD方法爆炸压力分布图

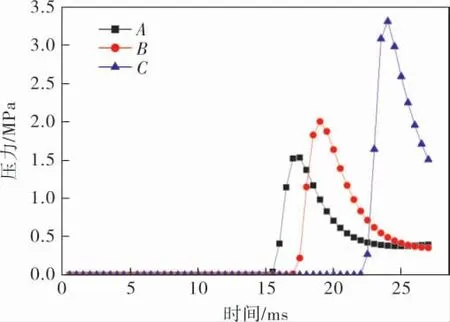
图4 CFD方法测点压力曲线

由图3可以看出，使用CFD方法模拟燃烧爆炸时，可燃气云燃烧形成了一个球形波，而且火焰接触到储罐罐壁时可燃气体仅发生了部分燃烧。 由于火焰扩散是一个逐层燃烧的过程， 因此可以看到球形波外层的压力要大于内层。 从图4可以看出，A点在15ms时检测到了压力，压力数值在17ms时达到峰值1.53MPa， 随后逐渐下降直到稳定在0.40MPa左右。B、C点由于距离起爆点较远，因此测得压力的时间相对滞后。但是B点测得的峰值压力（2.01MPa） 为A点的1.31倍，C点测得的峰值压力（3.31MPa）为A点的2.16倍。 由此可以看出，使用CFD方法模拟爆炸时，距离点火点越远，爆炸压力越大。这是因为在燃烧初始阶段，虽然爆炸波先到达近爆点A，但是此时罐内可燃气体并没有完全燃烧。 随着时间的推移，可燃气体边燃烧边扩散，压力波依次到达B点和C点， 此时罐内可燃气体绝大部分已经发生反应，产生的压力也就更大。因此B、C点测得的爆炸压力也就更大，最终出现了测点距离起爆点越远爆炸压力越大的现象。

2.2 TNT当量法计算储罐内可燃气云爆炸载荷

TNT当量模型的工况设置与CFD方法相同，计算后仅提取N2起爆点的爆炸数据，爆炸波刚接触到罐壁时的压力分布如图5所示， 各测点的压力变化曲线如图6所示。

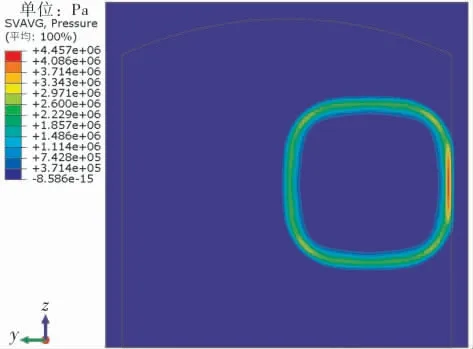
图5 TNT方法爆炸压力分布图

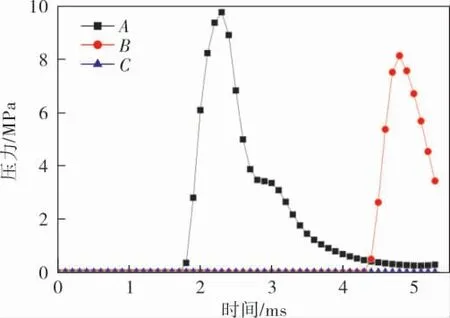
图6 TNT方法测点压力曲线

从图5可以看出，TNT当量法模拟出来的爆炸压力以环形波形式扩散，爆炸发生后中心区域的压力与压力波未到达的区域压力数值相同。 由于爆炸波接触到罐壁后形成了反射波，因此罐壁附近的压力数值较大。 与CFD方法不同，图6所示的A点在1.8ms时就检测到了爆炸压力，并且压力峰值达到了9.78MPa，是CFD方法的6.39倍，并且压力到达峰值之后在2ms内迅速下降为零。B点的峰值压力为8.15MPa，较A点下降了20%。 压力波在到达C点之前结构已经发生破坏，因此C点未检测到爆炸压力。由此可以得出结论，使用TNT当量法计算储罐内可燃气云爆炸载荷时，测点离起爆中心越远爆炸压力越小。

综上所述，使用CFD方法时，爆炸压力随着距爆炸中心距离的增大而增大；使用TNT当量法时，爆炸压力随着距爆炸中心距离的增大而减小。 由于CFD方法和TNT当量法本质上的不同，导致在相同工况下，二者得到了完全不同的压力变化规律。

3 不同等效方法下的储罐内爆结构破坏分析

3.1 CFD方法储罐内爆结构破坏分析

使用CFD方法研究储罐结构破坏时需要借助Abaqus来进行模拟。 使用Mpcci来完成Fluent与Abaqus之间的数据传递， 由此实现CFD方法模拟储罐结构在可燃气云爆炸载荷下的破坏。 限于篇幅，此处仅出具爆源距罐壁1m时不同容积储罐的破坏位置（图7）。

图7 不同容积储罐的破坏位置

从图7a可以看出，整个储罐壁板都产生了应力和变形， 储罐破坏位置位于左侧顶壁连接处。由2.1节可知， 爆炸压力随着爆心距的增大而增大，因此3 000m3储罐左侧顶壁连接处承受的爆炸压力最大。 同时，储罐顶壁连接处属于结构不连续位置，容易发生应力集中。 因此，顶壁连接处较储罐其他位置更容易发生破坏。 对比图7可以发现，随着储罐容积的增大，破口位置逐渐由左向右转移。 这是因为随着储罐容积的增大，罐内可燃气体的质量也在增大，气体燃爆产生爆炸压力也就更大。 此时，燃爆产生的球形火焰波还未到达最左侧顶壁连接处，燃爆的压力已足以使结构发生失效破坏。 因此，随着容积的增大，破口位置不再出现在最左侧顶壁连接处，并逐渐向右侧转移。 同时，储罐的变形呈现上大下小的葫芦状，这是由于本课题中储罐模型采用了变壁厚的设置，越靠近罐顶位置、罐壁厚度越小，所以储罐上半部的变形比下半部更大。 为了避免储罐结构大变形引起的单元畸变，本次计算使用J-C强度模型和相应的失效准则［18］，公式如下：

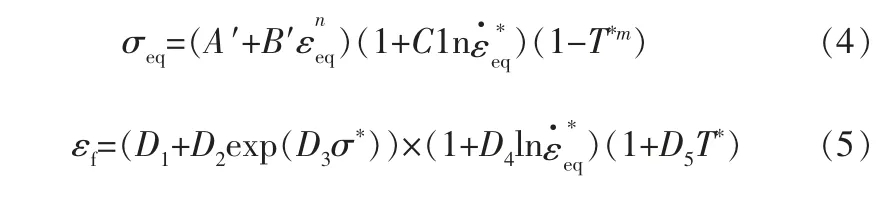
其中A′、B′、C、n、m为模型参数；εeq为等效塑性应变；σeq为等效应力；εf为失效应变；为等效塑性应变率；T*为无量纲温度；D1～D5是材料常数；σ*为材料应力三轴度。 由此可见，J-C强度模型和失效准则均与应变率相关，等效应力和失效应变是随着应变率的变化而不断改变的。 笔者在统计储罐破坏应力时发现，储罐破坏伴随着单元的删除，单元删除的瞬间应力变化幅度很大。 为了分析起爆点不同时储罐结构破坏的规律，试验中提取的数据为破坏前0.5ms时的数据，得到储罐的最大应力及径向变形（表1）。

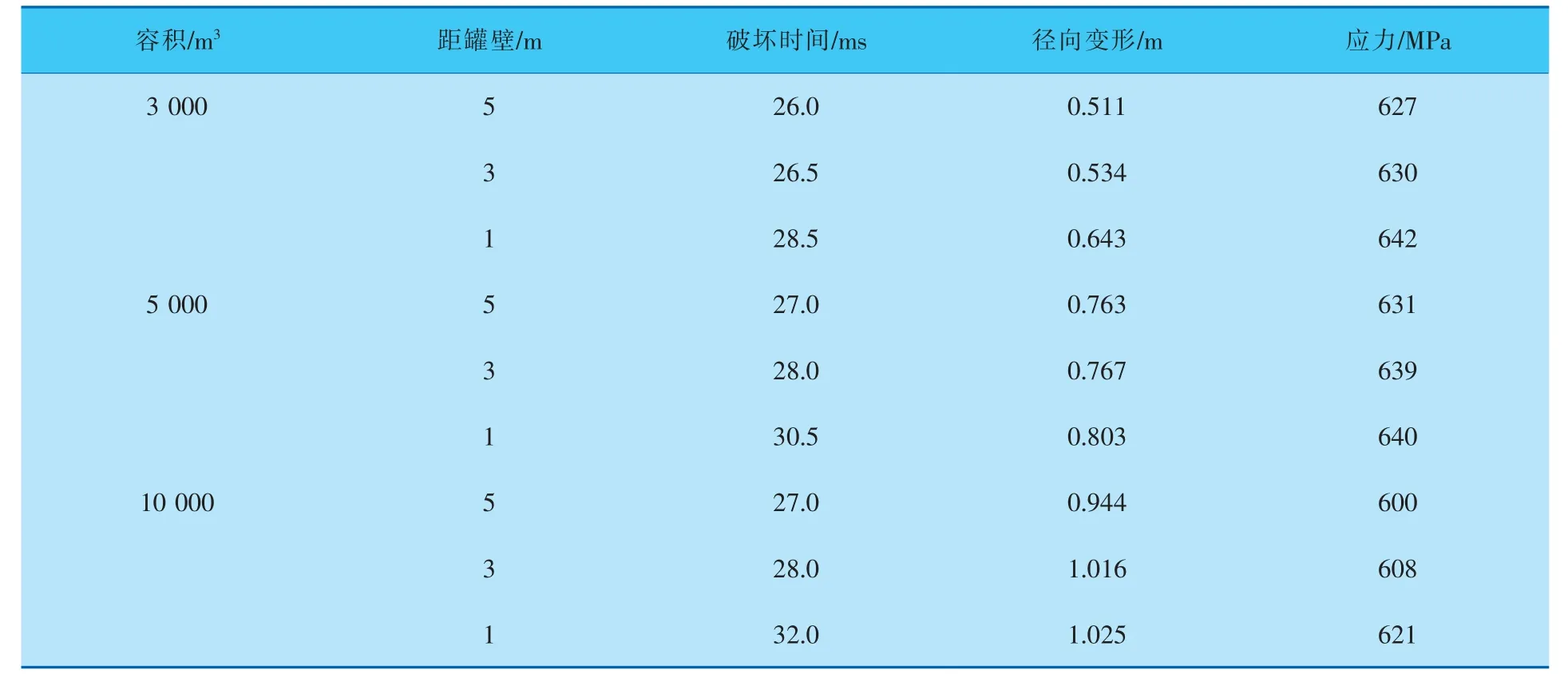
表1 不同容积储罐应力及径向变形量

由表1中3 000m3储罐破坏数据可以看出，随着点火点越靠近罐壁，储罐结构破坏时间逐渐增加，径向变形也越来越大。 由于点火点越靠近罐壁，燃烧产生的火焰波到达左侧顶壁连接处的时间越长。 同时，爆炸压力也随着时间的增加而增大，因此变形也就随之增大。 由式（4）、（5）可知，结构破坏时的应力与应变率相关，而应变率的大小取决于爆炸压力作用在结构上时间的快慢。 不同工况下储罐破坏时的应变率不同，因此储罐破坏时的应力也就不同。 在储罐容积增大的过程中，随着罐内可燃气体量的大幅增长，储罐的应力、变形都没有很大变化，这是由不同容积的储罐壁厚不同导致的。 为了保证结构的强度，随着储罐容量的增加， 储罐的壁厚也会相应增大，壁厚的增加限制了储罐应力和变形的大幅提升。

3.2 TNT当量法储罐内爆结构破坏分析

综合考虑储罐罐体结构、罐体内外空气域和可燃气体的TNT当量质量， 模型中爆炸产物与结构之间采用CEL流固耦合算法， 起爆点位置与CFD方法采用相同设置， 最终得到不同起爆点时储罐应力分布及破坏位置（图8）。

由图8a、b可以看出，3 000、5 000m3储罐的破坏位置均为近爆侧顶壁连接处，同时储罐罐壁位置出现了较大凸起。这是由于TNT爆炸时，距离爆炸中心越近，结构承受的压力越大，爆炸产生的超压使储罐罐壁发生局部大变形。 当爆炸波继续传递到达右侧顶壁连接处时， 由于该位置是结构不连续区域，因此该位置先发生破坏。 而从图8c可以看出10 000m3储罐爆炸破坏位置为罐壁。这是因为10 000m3储罐换算的TNT当量质量足够大，虽然同样是在距离罐壁1m位置处爆炸， 但10 000m3当量TNT爆炸产生的超压足以使储罐罐壁直接被破坏。为了得到更准确的储罐破坏时刻，采用TNT当量法分析时设置的时间间隔为0.1ms。 提取3种不同容积的储罐在不同起爆位置破坏时的参数，具体见表2。

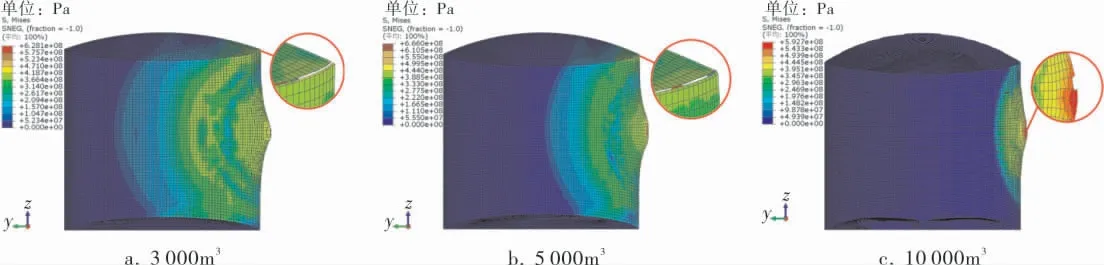
图8 不同容积储罐应力分布及破坏位置

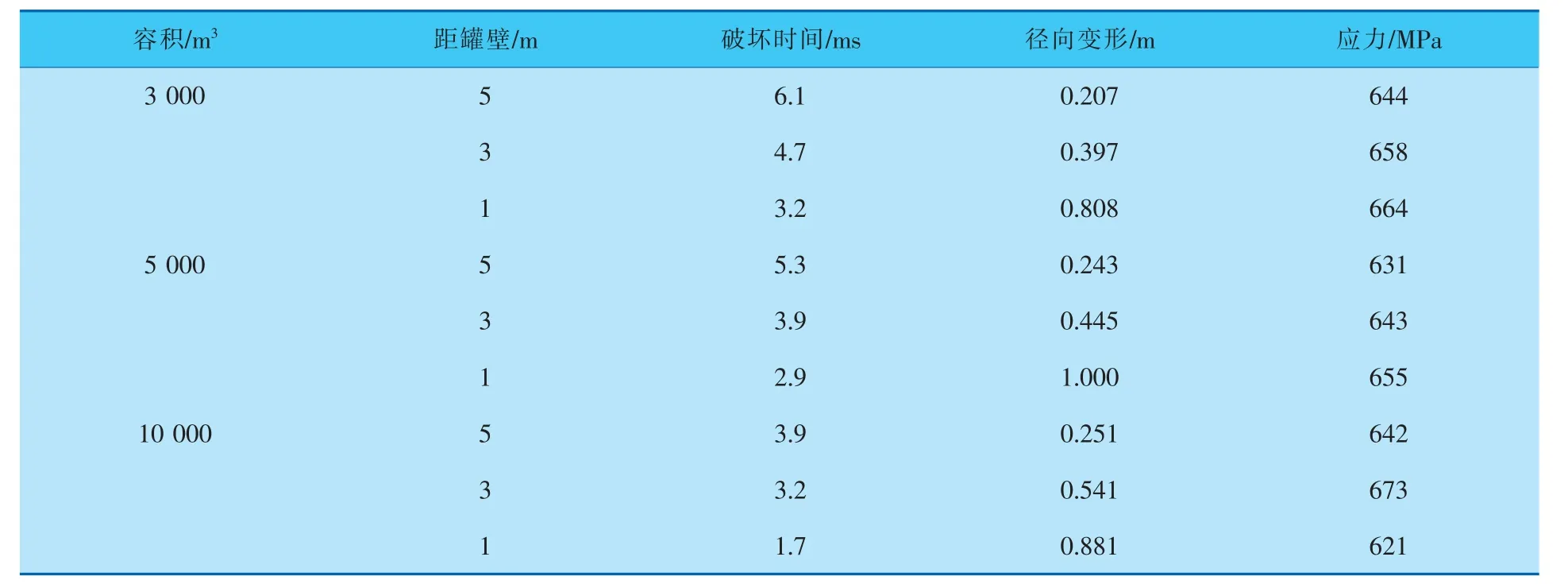
表2 不同容积储罐应力及径向变形

从表2可以看出， 当储罐容积相同时，TNT起爆位置每靠近罐壁2m， 径向变形增量超过80%。这是由于TNT爆炸产生的超压在空气中损失很大，爆炸冲击波每向前传递1m，爆炸压力就会大幅下降。 观察不同容积储罐的破坏时间可以发现，随着容积的增大，爆炸破坏时间变短，这是由于TNT当量变大后，爆炸瞬间产生的压力越大，破坏时间越提前。

3.3 不同等效方法下储罐内爆结构破坏对比分析

为了分析CFD方法和TNT当量法各测点位置结构应力变化情况，对5 000m3储罐，在距罐壁5m起爆位置工况中， 分别提取两种方法A、B、C点的压力和应力时程曲线如图9、10所示。

图9 不同方法压力时程曲线

图10 不同方法应力时程曲线

由图9可以看出，TNT当量法在A点和B点得到的压力远大于CFD方法。 TNT当量法的爆炸压力波经过A点的压力峰值为9.8MPa，CFD方法的压力波经过A点的压力峰值仅为1.9MPa， 二者相差超过80%。 B点的压力峰值也相差了近74%。 C点由于在储罐破坏前没有检测到压力，因此仅有CFD方法的压力曲线。通过观察图10可以发现，两种方法的A点应力变化趋势相同， 但是CFD方法的应力出现时间和上升速度都较小。 TNT当量法的B点出现了单元删除，因此应力值在发生剧烈增大后下降为零，CFD方法的B点与A点趋势一致，仅应力出现时间略有增大。 两种方法C点位置的单元没有发生失效，因此CFD方法的应力在结构破坏前持续上升，而TNT当量法未检测到压力，也就没有产生应力数值。 为了分析不同爆炸模拟方法对储罐结构破坏位置的影响，分别提取CFD方法和TNT当量法模拟后的储罐破坏位置，具体见表3。

表3 不同容积储罐破坏位置

由表3可以看出，相同容积的储罐采用CFD方法时破坏位置相同， 而且随着储罐容积的增大，破坏位置逐渐由左向右转移。 TNT当量法计算得到的储罐破坏位置大部分位于右侧顶壁连接处，而10 000m3储罐的破坏位置发生了改变， 起爆点距罐壁1m时储罐的破坏位置为近爆点罐壁。破坏位置的改变是不同容积储罐的TNT当量不同导致的。采用CFD方法得到的储罐破坏时间差别不大，最大时长与最小时长仅相差25%； 采用TNT当量法得到的储罐破坏时间相差较大，最大时长与最小时长相差超过72%。

4 结论

4.1 采用CFD方法和TNT当量法研究储罐内爆载荷时，CFD方法的爆炸载荷传递速度要低于TNT当量法。 在同一测点TNT当量法检测到压力的时间仅为CFD方法的1/10，同时TNT当量法近爆测点A的峰值压力是CFD方法的6.39倍。 使用CFD方法时， 爆炸压力随着爆炸中心的距离增大而增大；使用TNT当量法时， 爆炸压力随着爆炸中心的距离增大而减小。

4.2 采用CFD方法和TNT当量法研究储罐结构破坏时，CFD方法计算出来的结构破坏位置位于远离起爆点的左侧顶壁连接处，并且随着储罐容积的增大逐渐由左向右转移。 TNT当量法多数工况储罐破坏位置位于近爆点顶壁连接处。 当TNT当量质量足够大或者TNT与罐壁距离足够近时，储罐在近爆点罐壁发生破坏。 采用CFD方法得到的储罐破坏时间差别不大，最大时长与最小时长仅相差25%； 采用TNT当量法得到的储罐破坏时间相差较大，最大时长与最小时长相差超过72%。

4.3 由于可燃气体逐层燃烧的特性，CFD方法的爆炸压力随着爆心距的增大而增大，使得距离点火点较远处的结构承受较大的压力，因此远爆点处的结构先发生破坏。 而TNT当量法计算爆炸载荷时，爆炸压力是瞬间释放并逐渐降低的，此时近爆点结构会承受更大载荷并发生破坏。 正是两种等效方法本质上的不同导致了模拟结果的规律不一样。 CFD方法模拟的爆炸在结构与爆源较近时爆炸强度较低， 此时TNT当量法模拟可燃气云爆炸产生的超压峰值最大相差80%。 当结构与爆源相距较远时，两种方法模拟出的结构破坏趋于一致。