网络协同设计过程的任务分解算法模型研究*
四川大学机械工程学院 成都 610065
0 引言
云制造是一种面向服务、高效低耗和基于知识的网络化、敏捷化制造新模式和技术手段,它将促进制造的敏捷化、服务化、绿色化和智能化[1]。一方面用户可以根据应用需求,随时随地、动态、敏捷地增减制造资源,获得优质服务;另一方面接入云制造的中小规模企业形成虚拟联盟,统筹协作,较好地平衡了资源的不足和过剩并存的冲突[2],更极大地丰富了成员企业的制造资源,提高了中小规模企业的制造能力,使其能够分解消化更大型的制造任务,具备能够与大型集团同台竞技的能力,对于制造业升级转型具有重大意义。
合理的任务分解方法能够科学分解制造任务,获得合理的子任务拓扑结构,使云环境下的资源匹配吻合度高,资源利用效率高。相关研究如文献[3]通过构建扩散任务相关性模型,结合粒子群聚类优化分解算法,实现对扩散任务的有效分解,文献[4]在制造任务分解的时考虑了任务之间的关联性,更加适合于云环境下的制造场景,为研究制造任务的分解提供了思路和准则。
根据制造任务分解的三大原则[5]:自下而上的分解原则、能整不分的分解原则以及能分不拆的分解原则。首先研究任务模型的表达,然后基于层次分解的思想,再综合考虑相关性、内聚性等评价指标,利用改进的顺序任务分解方法(OTD)实现云环境下的制造任务分解。
1 云环境下的任务表达方法
1.1 云环境下的任务模型
物元模型[6]是易于计算机存储、识别和操作的实体对象的表示方法,广泛应用于目标的模型表达。本文应用物元模型将一项云端制造任务Tk,具体描述了任务本身的各项需求和约束以及用户的相关期望等,Tk可表示为

式中:Tki为制造任务Tk的第i个子任务,而且每项可分子任务Tki可用三元组描述如式所示;Ta为子任务Tki的属性集合;To为子任务Tki的状态集合;Tu为子任务Tki的服务消费集合,依据相关性、内聚性等评价指标,逐级分解到各项子任务均具有不可再分的任务粒度。
对于具体任务Tki,用七元组描述一项不可再分的子任务的属性集合Ta=(ID,Na,Co,Ti,Qu,Eq,Re)。其中ID为任务编码,Na为任务名称,Co为任务成本约束,Ti为任务时间约束,Qu为任务的质量要求,Eq为任务特殊装备要求以及Re为用户的其他要求。用二元组表达子任务Tki的属性状态集合To=(TL,TS),TL为该子任务的次级子任务ID列表,TS为其执行状态列表,若该级子任务不再包含子任务,则其已拥有了原子性(不可再分的任务粒度),用二元组表达子任务Tki的服务消费集合Tu=(Re,Po),其中Re是累计成本,Po是累计消费时间。
1.2 任务分解指标构建
任务分解的层级及子任务的数量和粒度控制是云制造任务分解的关键,直接影响云制造任务协同完成的质量、执行进度和成本。因此,研究任务分解时子任务之间的关联关系和内聚性对任务执行的效率和成本至关重要,在学习现有研究的基础上构建了关联性度量、内聚性度量和任务粒度评估等指标,对任务分解过程进行控制。
1)任务粒度St
任务粒度层数越深,任务粒度越小,任务个数越多,任务粒度越小,故任务粒度的量化可表示为

式中:St为任务粒度量化指标;La为子任务层数;N为子任务个数,&为引入的粒度系数。任务层次分解时每一层的任务粒度需要设定阈值、严格控制,保证任务的原子性,为次层级的任务分解做好基础准备。
2)内聚性Pt
内聚性是模块构建的基本目标,是软件构建内联关系的表征。定义为:若M的执行需要调用或等待N的完成或执行,则M调用依赖于N,一个方法M依赖于方法N,则记作M→N。
由于子任务具有较高模块性,故引入内聚性来度量子任务内部活动单元之间的关联程度,然后求平均值来综合评价该项任务的内部关联程度以判断其分解效果。由于任务存在较多的约束(时间约束、成本约束和质量约束等),然而这些约束之于任务并不能完全等同于软件工程中的变量之于方法,故而本文提出以多约束下的模块内聚度计算方法,即


式中:f(n)为在约束k下的第q个子任务的内聚度量化指标;n为第q个子任务内部的活动数量;f(i)为第q个子任务的第i个活动与其相关活动的内聚度指标,是f(n)中f(i)的具体量化形式;f(k)为与活动i相关的第k个活动;M为活动k的内聚度,如果k为不可再分的活动,则其M=1,否则M的值按照式(3)进行递归计算;Pt为内聚度指标;Q为某任务分解过程中的约束个数。
3)相关性Rt
云环境下的制造任务种类多、活动丰富,强约束性(尤其是时序约束)的存在使制造任务的相关性异与软件构构件中的方法关系,同时一项制造任务的完成依赖于各子任务间的信息交互和物流交通,故任务分解过程需要考虑到任务的独立性及其相关性,本文应用模糊理论来构建了信息矩阵和理论物流矩阵来描述任务活动间的相关关系。

图1 半岭分布型隶属度函数
考虑到模糊知识的获取应该去极端化,体现出一般性规律,本文采用半岭型分布作为专家术语隶属度函数,再考虑参与评价专家总数和评价术语出现次数(专家评价采用0-9打分法)[7],建立制造任务关联关系的量化模型为
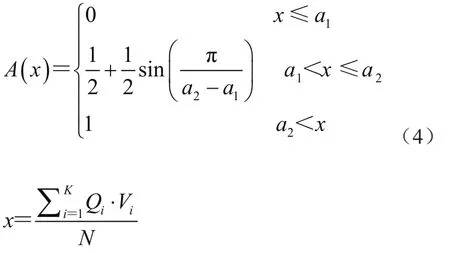
式中:N为参与评价的专家人数,Qi为专家对两个制造任务的关系的第i项评价值,Vi为对该关系做出相同评价值的专家人数,由此计算所得的x可认为是对于两个制造任务关联关系的综合经验描述,然后将其带入到半岭分布当中计算其隶属度值aij,则aij能基于专家知识和模糊理论量化两个制造任务i、j之间的关联程度。以aij为元素,构建如下信息关联矩阵A,同理获得物流关联矩阵L为
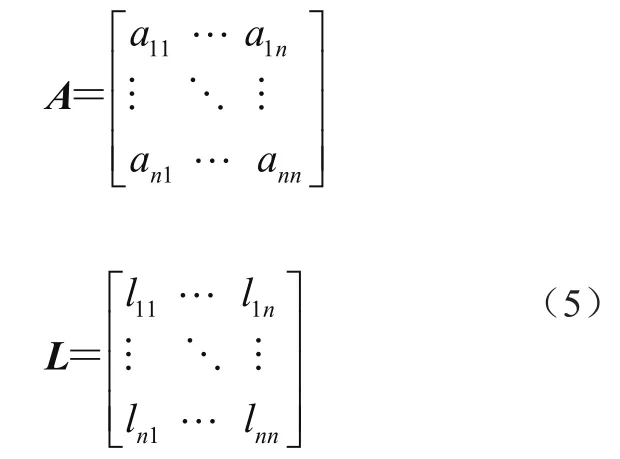
考虑到制造任务的多样性,如设计任务主要以信息交流为主,很少产生实际的物流交互,生产加工类任务则需要信息交互和物流交互双向沟通,故任务i和任务j的任务关联度综合描述为
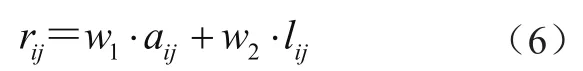
以rij为元素的三角对称矩阵R反映了各项任务的关联关系,其中w1和w2为不同任务类型下关于信息关联和物流关联的权值,任务分解时秉承着各子任务内部聚合度高,子任务间关联弱的原则,故需设定关联度阈值Rmax>∞-范数(矩阵R)。
2 改进OTD方法
2.1 OTD方法
传统的OTD算法是基于分层任务网络(HTN)规划方法[8,9]来研究任务分解的方法,一般将一个任务分解问题表示为四元组q=(s0,w※,Os,Ms),其中s0为问题的数学模型,w※为初始任务网络状态,Os为操作集合,Ms为分解方法集合。该算法的运行流程为:
1)从初始状态w0※开始,选择一个可转换为复合任务的简单任务ei,任取一个方法mj∈Ms对ei进行分解;
2)总任务网络N※及子任务网络集Ns※形成来描述分解目标;
3)对任务网络进行评价指标分析计算并判断是否达标,若达标则执行步骤4,否则返回步骤1;
4)输出分解结果并结束算法。
传统的OTD算法主要使用分解方法对任务进行分解,判断其可行性,如若不可行则重新开始分解。然而任务分解的粒度太小、层级太深会使任务间的关系复杂,造成信息交互困难和物流紧张,增加任务执行和管理难度,任务活动太少、粒度太大,直接导致任务内部复杂度高。任务个数和层数不是强相关的两个变量,能否通过改变任务数量而不增加任务层数,或反之来控制粒度大小和实现分解目标。
2.2 改进的OTD方法
传统的OTD方法并未考虑到任务分解到某一解状态S距离目标解的距离,也未考虑到变异分解状态来获得其他形式的解以保证解空间的多样型,为了解决上述问题,本文研究了改进OTD算法,在计算评价指标、判断可行性之后根据指标更改变换N※和Ns※寻找实现目标任务网络的状态,对于改进的OTD算法详述为:任务分解问题表示为四元组q=(s0,w※,Os,Ms),其中s0、w※、Ms的含义与传统OTD方法无异,引进操作方法集合Os来描述变换N※和N※s的启发式操作算子。Os为一个算子集合,相比于传统的OTD操作。本文提出了搜索压力算子集OP来描述当前解所在状态距离目标解的距离及其搜索方向,OP的具体内涵可表示为

式中:Oi为集合Op的第i个元素,Oi的解析式是关于内聚性、任务粒度以及相关性的函数形式,如再在判定当前分解状态下的St过小,当Pt、Rt均复合条件时,则可选定增大St的算子对当前状态进行修改,使之成为无违规约束的可行解,传统OTD与本文改进的OTD之间的流程差异如图2所示。

图2 半岭分布型隶属度函数
如图2所示为改进OTD算法,该方法借鉴启发式算法的思想,根据每次迭代的相关性、内聚性以及任务粒度值来判断当前解所在状态距离目标解的距离以及方向,并据此来设定相关算子以形成搜索压力,使得当前解向着目标解的方向进行搜索。
3 实例应用
为了验证上述方法的有效性和可行性,本文以固定卷扬式启闭机的制造任务分解为例,对文中提及的任务分解方法进行验证,并根据用户要求设定Pmax-t=2.5、8<St<10、对于每个子任务的Rmax-t=0.5,对于n个子任务,任务的Rmax-t=0.5n,进行云环境下的制造任务分解。
启闭机的制造任务主要包括标准件定制和非标件生产两个步骤,根据装配需求,其制造任务的约束主要以时序约束为主,任务分解的方法集合包括时序可分Tm和功能可分Fm,响应的根据相关性、内聚性和粒度的可压缩值,Os集合包括Rt改进方法Rm、St改进方法Sm以及Pt改进方法Pm。在此,以Pm对固定卷扬式启闭机的制造进行任务分解,对比传统的OTD方法,突出本文所论改进的特点所在。
3.1 基于功能的OTD分解实例
基于启闭机的功能分解方法Fm进行任务分解,启闭机根据功能分解方法Fm根据OTD算法可将其分解为如图3所示的制造任务结构。

图3 基于功能的启闭机制造任务OTD分解
1)Pt的计算
根据任务分解结果进行Pt、St、Rt值计算,并验证是否满足要求,对于St根据式(5)进行计算有St=(1+0.2)×3+20÷3=10.23,系数1.2为用户在任务注册时,希望得到的任务分解层数系数(用0~1量化用户对任务层数的期望,0.5表示用户对层数深度没有必要的要求,1是任务层数对任务粒度影响的固有系数)。
2)St的计算
St的量化方法如式(6)所示,在卷筒制造任务中,筒壁要根据卷筒轴的实际形状尺寸进行装配形成卷筒部件,筒壁制造依赖于卷轴,故以卷轴、筒壁为活动,计算卷筒制造子任务T1的内聚度有

则基于功能分解

即卷筒结构的内聚度值为2。同理,以钢丝绳、卷筒和轴承座的制造为活动,计算卷扬机构的内聚度,由于钢丝绳与卷筒相关,轴承座与卷筒相关,钢丝绳与轴承座无依赖关系,且有根据上述计算M(卷筒)=2,故在计算卷扬机构聚合度时有

由此可见,Pt(卷筒)= 2 >Pt(卷扬机构)= 1.67。由于卷轴与筒壁两个活动全相关,而钢丝绳与轴承座存在不相关关系,也证明了内聚度计算方法的科学性,依次计算的Pt(启闭机制造)= 1.74。

3)Rt的计算
相关性Rt的计算,根据专家经验和专业知识,对于20个具有执行属性的子任务,根据专家给予的信息矩阵和物流矩阵,并赋予w1=0.7和w2=0.3,获得相关性关系矩阵R,并计算得R∞-范数=7。
3.2 基于功能的改进OTD分解实例
为了不增加任务层数,构建方法集合OP改进分解结果,由前所述Pt=1.74、St=10.23、Rt=7,对比与用户需求明显只有Smax-t=10<St=10.23,违反了粒度值的约束,故从构建的方法集合Op中选择一个方法来对已有的任务结构进行变换。
由于Pt和Rt相比于分解需求,均具距离用户设定极值有较大的程度,故从Op中选择MR(即通过增大Rt值使得其他指标满足要求)对任务分解结构进行改进,以求通过牺牲Rt来增加St使任务分解尽早满足约束。具体表现为减小任务个数,将耦合度高的子任务合并到一个子任务,运用Op中选择MR的任务分解结构见图4。

图4 基于功能的启闭机制造任务改进OTD分解
再根据前述的方法计算得St=9.6,Pt=1.67,R∞-范数=8.1,各项指标均满足分解约束。

3.3 结果分析
将OTD与改进OTD该方法对该任务进行分解后获得的任务粒度、内聚性和相关性对比如图5所示。由图5可知,改进OTD方法通过牺牲空间较大的指标(相关性)来使得降低违反约束的指标值,改变接尽可行解的拓扑结构,获得可行解。相比于传统的OTD,改进OTD方面在接近可行解上修改任务的拓扑结构。因此,改进OTD寻找的解更具多样性,且能避免分解步骤重新开始。
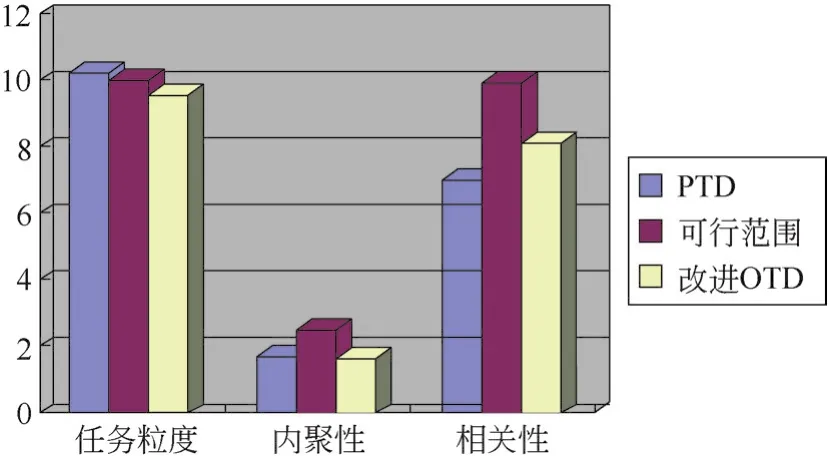
图5 效果对比
4 结论
1)应用物元模型建立云环境下的制造任务模型,并充分考虑了其属性、分解状态和执行状态,所研究的模型能胜任云制造中的任务表达、存储和展示;
2)对比传统OTD方法,本文研究的改进OTD方法能够在接近可行解上修改任务的拓扑结构,调整分解指标,获得分解结果。然而,如果分解过程中出现的接尽可行解难以通过算子Op改进获得可行解,运行算子Op将消费一定的时间;
3)以固定卷扬式启闭机的云制造任务分解为例,对所提方法进行了验证。

