SMW工法中不同影响因素对桩身的影响研究

田浩帆，包太，游帅，邓智中，田镇伟

(贵州大学， 贵州 贵阳 550025)

0 引言

在现代城市修建的深基坑工程中，基坑的优化设计尤为重要，SMW工法是Soil-cement Mixing Wall的缩写，于1976年在日本首先应用。该工法构造简单，与地下连续墙相比结构整体性和防水性能均较好，施工时噪音小、对周围环境破坏程度小、结构强度可靠，速度快、能大幅度地缩短工期，同时，由于H型钢可在后期从水泥搅拌桩拔出，对型钢材料可回收再利用，符合可持续发展的理念[1-3]。目前，该方法现已广泛应用于世界各地，近几年在上海、杭州、南京等地也迅速推广并应用。

基坑开挖过程中，对于地表建筑、管线等的影响是不可忽略的，可通过数值模拟或者理论计算减少对地表建筑物的负面影响[4-6]。桩身变形及内力产生的原因有很多，本文通过探究不同影响因素下的桩身变形及内力变化规律，为控制桩身形变及最大内力值提供一定的参考依据。

1 工程概况

本工程位于天津市临港工业区，以SMW工法为施工背景，地面堆载为20 kPa，预开挖深度为7 m，地下水深为1.5 m，采用厚度为1 m的搅拌桩围护结构，共设两道支撑，桩顶标高为0 m，在搅拌桩中加型钢，型钢惯性矩为2.01×105cm4，型钢间中心距为1000 mm。场地地质条件参数和工况见表1和图1。

2 基坑稳定性验算

基坑的稳定性验算包括多方面的验算，参照国家行业标准《建筑基坑支护技术规程》JGJ 120-2012）以及上海市标准《基坑工程设计规程》[7-9]，依次对其进行极限平衡嵌固深度验算、抗管涌验算、墙底抗隆起验算、坑底抗隆起验算、对于带支撑的，还要进行抗倾覆验算，最后再进行整体性验算。

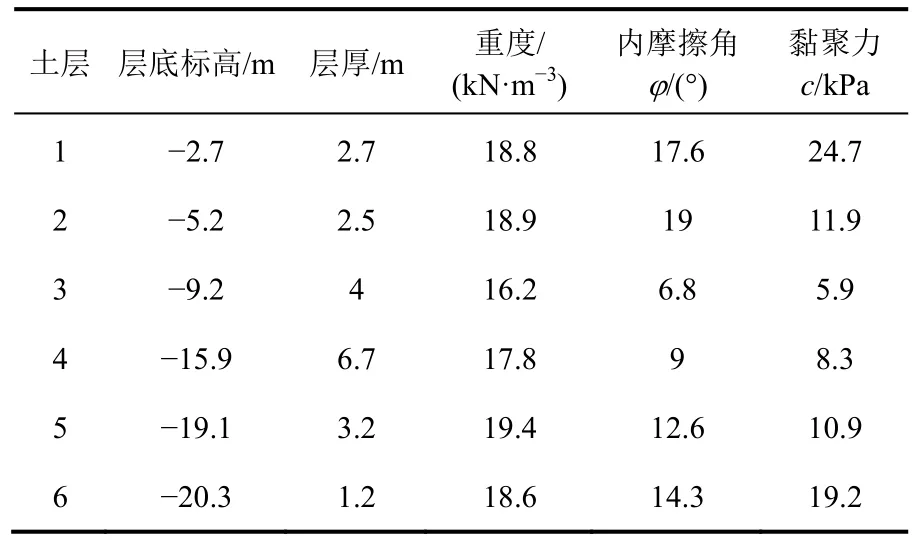
表1 地质条件参数

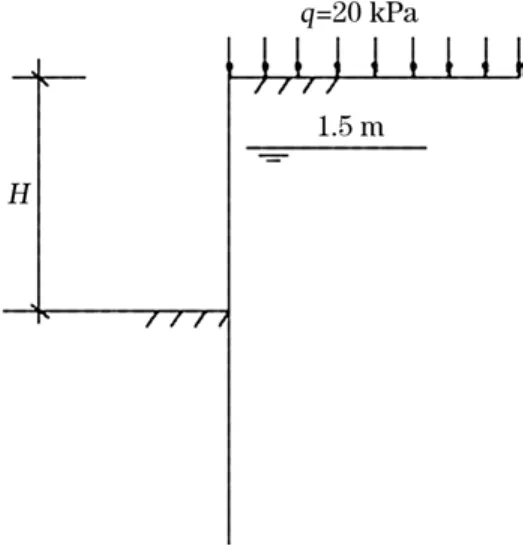
图1 工程基本情况

（1）极限平衡嵌固深度验算。先按确定的水、土压力模式计算围护结构两侧压力相等的点后按等值梁法确定支撑轴力T1、T2、…，再按下式计算压力比和力矩比。

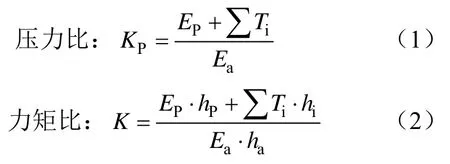
（2）抗管涌安全系数。对于砂类土：

对于黏性土：

（3）墙底抗隆起验算。根据 Terzaghi解，抗隆起安全系数为：

（4）坑底抗隆起验算。坑底抗隆起验算类似于圆弧面整体稳定验算，但圆心取最下一道支撑与挡墙的交点，并且圆弧通过墙底端，最下一道支撑以下为圆弧滑动面，以上为竖直直线。圆弧面上的滑动力和抗滑力的求法与瑞典条分法一致（但考虑水平应力），竖直滑动面上的抗滑力为：

（5）稳定安全系数等于最下一道支撑以下围护结构两侧土压力对最下一道支撑点的力矩之比：

（6）整体稳定性验算。基坑的整体稳定性分析实际是对支护结构的直立土坡进行稳定性分析，采用圆弧滑动面简单条分法，按总应力法计算，并考虑水平应力的影响，整体稳定性计算见图2。

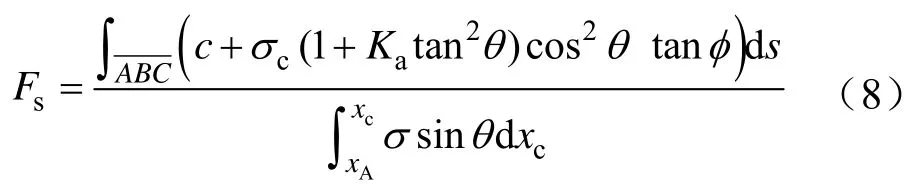
图2 整体稳定性计算

3 不同影响因素下的桩身变形及内力情况分析

通过控制不同桩径[10]，不同支撑位置及不同嵌固深度，通过计算工具分析其桩身变形及内力的变化规律。

3.1 不同桩径对桩身变形及内力影响

当嵌固深度为12 m，支撑位置为2 m和5 m时，分别选取桩径为0.6 m，0.8 m，1 m，桩身的内力及变形如图3所示。

由图3可发现，在SMW工法中，水平位移及内力值都随着深度的变化呈现出先增大后减小的趋势，同时随着桩径的逐渐变大，桩顶水平位移和桩身最大水平位移逐渐减小、桩身最大弯矩值位置约在7.75 m附近，桩径变化对其影响较小，最大弯矩值随着桩径变大而逐渐增大，桩身最大剪力值位置在5 m附近，当桩径为1 m时，最大剪力值位置在13.8 m处，可见桩径的逐渐变化对最大剪力值的位置也有一定影响，桩底水平位移随桩径增大而逐渐增大。桩身最大内力及变形见表2。

图3 不同桩径下的变形及内力

表2 不同桩径的桩身最大内力及变形

3.2 不同支撑位置对桩身变形及内力影响

当嵌固深度为12 m，桩径为1 m时，分别改变支撑位置为1 m和5 m、2 m和5 m、3 m和5 m时，桩身内力及变形如图4所示。

图4为SMW工法中桩身内力及位移的变化规律，当固定第二道支撑的位置固定在5 m处时，通过调整第一道支撑位置分别为1 m、2 m、3 m时，随着支撑位置的逐渐下降，桩顶的水平位移逐渐增大，桩身的最大水平位移先增大后减少，最大水平位移所对应的深度分别为8.5 m、8.25 m、6.25 m。由此可以看出，当支撑位置逐渐下调时，桩身最大水平位移点的深度也因其支撑位置的下调而向上抬升。桩身弯矩整体呈现出先增加后减少的趋势，最大弯矩值随其支撑位置的变化而逐渐减小，而桩身剪力值的出现和支撑位置有着密切的关系，即剪力值的出现点即为支撑点，同时最大剪力值随着支撑位置变化先增加后减少。桩底处水平位移整体变化并不是很明显。不同支撑位置的桩身最大变形及内力见表3。

3.3 不同嵌固深度对桩身变形及内力影响

在桩径为1 m，支撑位置为2 m和5 m时，嵌固深度D分别取11 m、12 m、13 m时，其桩身变形及内力如图5所示。

图4 不同支撑位置的桩身变形及内力

表3 不同支撑位置的桩身最大变形及内力

图5 不同嵌固深度下的桩身变形及内力

由图5可知，在SMW工法中，嵌固深度对桩身的形变及内力基本无影响，故无需再做分析讨论。

4 结论

在SMW工法中，桩径和支撑位置的改变能够对桩身的水平位移和开挖面的内力有一定影响，当桩径逐渐增加时，桩顶的水平位移随之增大，桩底水平位移则也随其增大，而桩身的最大水平位移则减少，桩身最大弯矩也增大。因此在实际工程中，如需控制桩身形变量，在满足设计要求的前提下可适当增大桩径。

当第一道水平支撑位置下降，第二道水平支撑不变时，桩顶水平位移增大，而桩身的水平位移先增大后减少，桩身最大弯矩值呈减少趋势，而桩底水平位移无显著变化。因此在实际工程中，如需有效控制桩身形变，可下调支撑位置来获得较优的支撑位置。嵌固深度对桩身的形变和内力影响可忽略不计。