基于HVD算法的负荷暂态事件监测
温伟伟,武金亚,王建元
(1.东北电力大学自动化工程学院,长春132012;2.贵阳航空电机有限公司,贵阳550025)
引 言
随着科学技术的快速发展,智能用电在生活中变得越发重要。家用负荷监测是实现智能用电的重要环节,为了获取每种电器的电能消耗情况和运行状态,负荷监测通过对总负荷的数据进行采样与分析,以监测每种电器的详细运行状态[1]。
传统的负荷监测需要在每个用电设备上安装一个传感器,消耗大量的人力物力。20世纪80年代麻省理工学院的Hart教授提出了非侵入式负荷监测(Non-intrusive load monitoring,NILM),NILM仅在用电设备入口处安装监测装置,通过采集入口处的电气参数,以达到对系统内部负荷的种类和运行情况的监测,实现负荷的辨识。非侵入式负荷监测分析方法主要分为稳态特征方法和暂态特征方法,稳态特征主要是指用电设备的稳态基波、谐波功率等特征,暂态特征主要指用电设备开启瞬间的功率、电流值等的变化规律。成功对用电设备的暂态事件进行监测是后期负荷识别及非侵入负荷监测的基础[2-4]。
本文针对负荷的电流特征进行暂态监测,电流值的大小会随着负荷开启或关闭时暂态过程而变化,将电流的变化应用到暂态监测的算法中,作为判断是否有暂态事件发生的识别标准。文献[5]提出了双边滑动窗CUSUM变点监测算法,该算法虽能监测到电气设备投切时所引起的暂态过程,但该方法受限于阈值的设定,存在漏检和误检。
针对上述算法存在的不足,本文提出了一种希尔伯特振动分解(Hilbert vibration decomposition,HVD)算法。HVD算法是一种非平稳信号处理方法,最早应用于机械的振动故障诊断,后来研究者又对频率波动、幅值突变等暂稳态谐波进行检测都取得了良好的效果[6]。HVD算法的家用负荷暂态事件监测方法,与双边滑动窗CUSUM变点监测算法相比,该算法无需设置阈值。利用MATLAB/Simulink软件搭建家用负荷仿真模型,结合本文提出的HVD算法对仿真结果进行分解,最终验证了该算法能够准确地对家用负荷的暂态事件进行监测。
1 希尔伯特振动分解算法
随着生活水平的提高,家用负荷的种类越来越多,当负荷在发生故障和投切等运行状态发生改变时,监测到的电流、功率等电气参数会随之发生变化,电气参数变化时会存在着突破点[7-8]。因此,家用负荷的暂态事件检测可以转化为电气参数的突变点监测。
1.1 Hilbert变换
对任何一个连续的非平稳信号X(t)的Hilbert变换为

原始信号X(t)与Hilbert变换信号Y(t)组成一对共轭复数对,得到X(t)的解析信号为
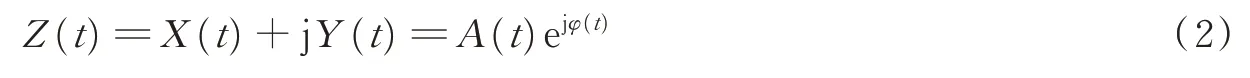
式中A(t)和φ(t)分别为原始信号X(t)的瞬时幅值和瞬时相位,对应的表达式分别为

因此瞬时频率对应的表达式为

1.2 幅值最大分量的频率估计
由于多分量频率和幅值的非平稳性,信号X(t)可表示为

式中:i为当前的分量编号,i=1,2,…,N,N为多分量的个数;Ai(t)、fi(t)分别为第i个分量的瞬时幅值、频率;θi、φi(t)分别为第i个分量初相位和相位。将信号X(t)经希尔伯特变换得到解析信号Z(t)表达式为

当N=2时,解析信号Z(t)可表示为
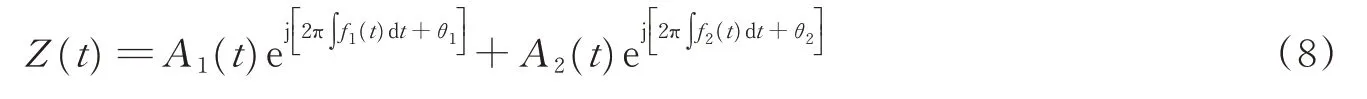
式中j为虚数。由解析信号得到X(t)的瞬时幅值A(t)表达式为
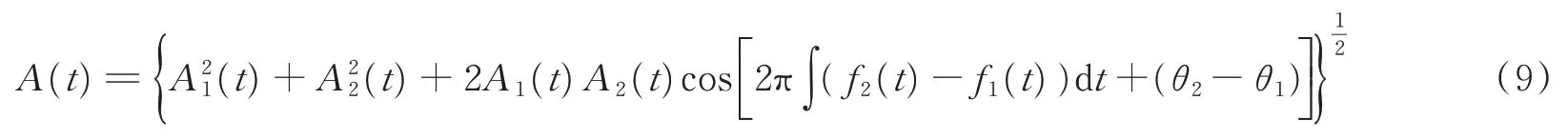
瞬时频率为
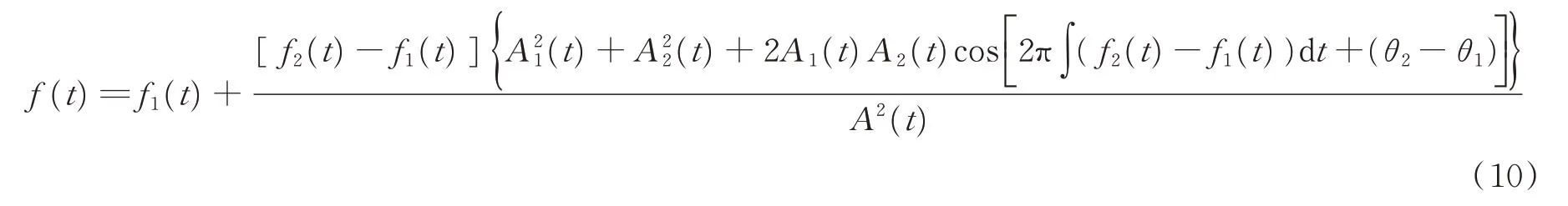
式中包含两部分:(1)幅值最大分量的瞬时频率f1(t),(2)快速变化的不对称振荡高频分量。实际应用中可用低通滤波滤除不对称振荡成分,则f(t)=f1(t)。
1.3 幅值和相位估计
将以上估计的瞬时频率看作为参考频率fr(t),同时经同步检测得到瞬时幅值Ar(t)和初相位θr(t),构造两个正交信号,将原始信号X(t)与正交信号相乘得同相输出X1(t)表达式为

正交相输出X2(t)表达式为
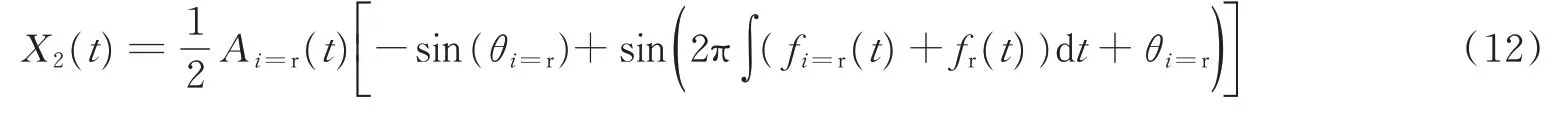
式(11)、式(12)与式(10)结构相同,同样可将后半部分用低通滤波器滤除,可得

从而可得到瞬时幅值Ar(t)和初相位θr的表达式分别为
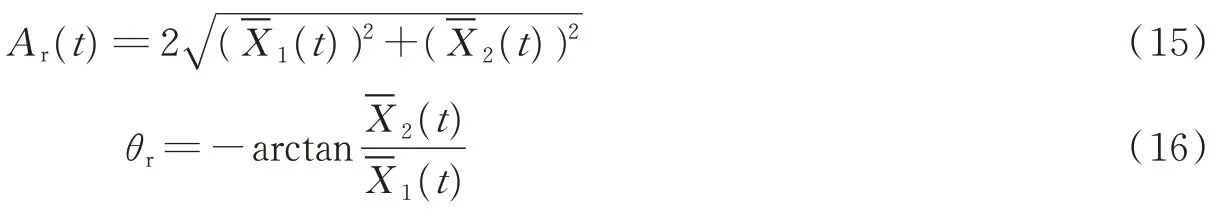
1.4 迭代运算
根据以上步骤提取当前原始信号X(t)中幅值最大分量,表达式为
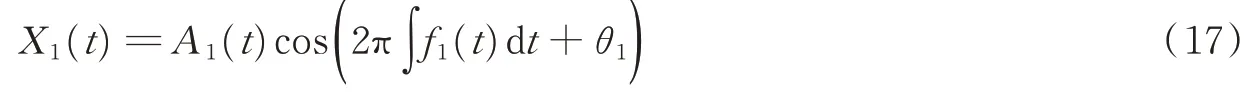
将原始信号X(t)与X1(t)的差作为初始信号,得

这样以此类推,将原始信号与当前幅值最大分量作差,差值作为初始信号继续执行HVD算法,直到差值标准差小于极限值0.001时,停止迭代过程。
2 仿真信号的HVD分解
选取一个有3个不同频率不同幅值的谐波信号为仿真信号
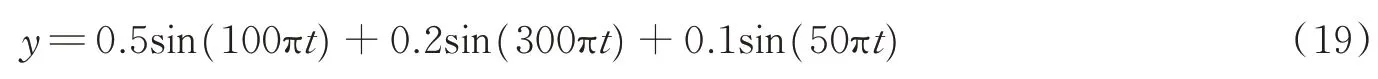
采样频率设为2 kHz,选取1 024个采样点,信号仿真时域波形如图1所示。
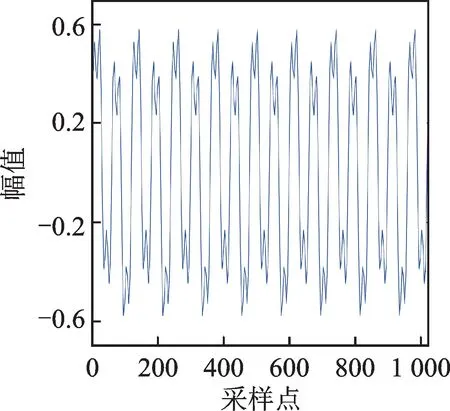
图1 仿真信号时域波形图Fig.1 Simulation signal time domain waveform
对该仿真信号进行HVD分解可以得出各谐波分量,如图2所示,且分解后各谐波分量的瞬时频率、瞬时幅值和原始信号数据保持一致,如图3所示。
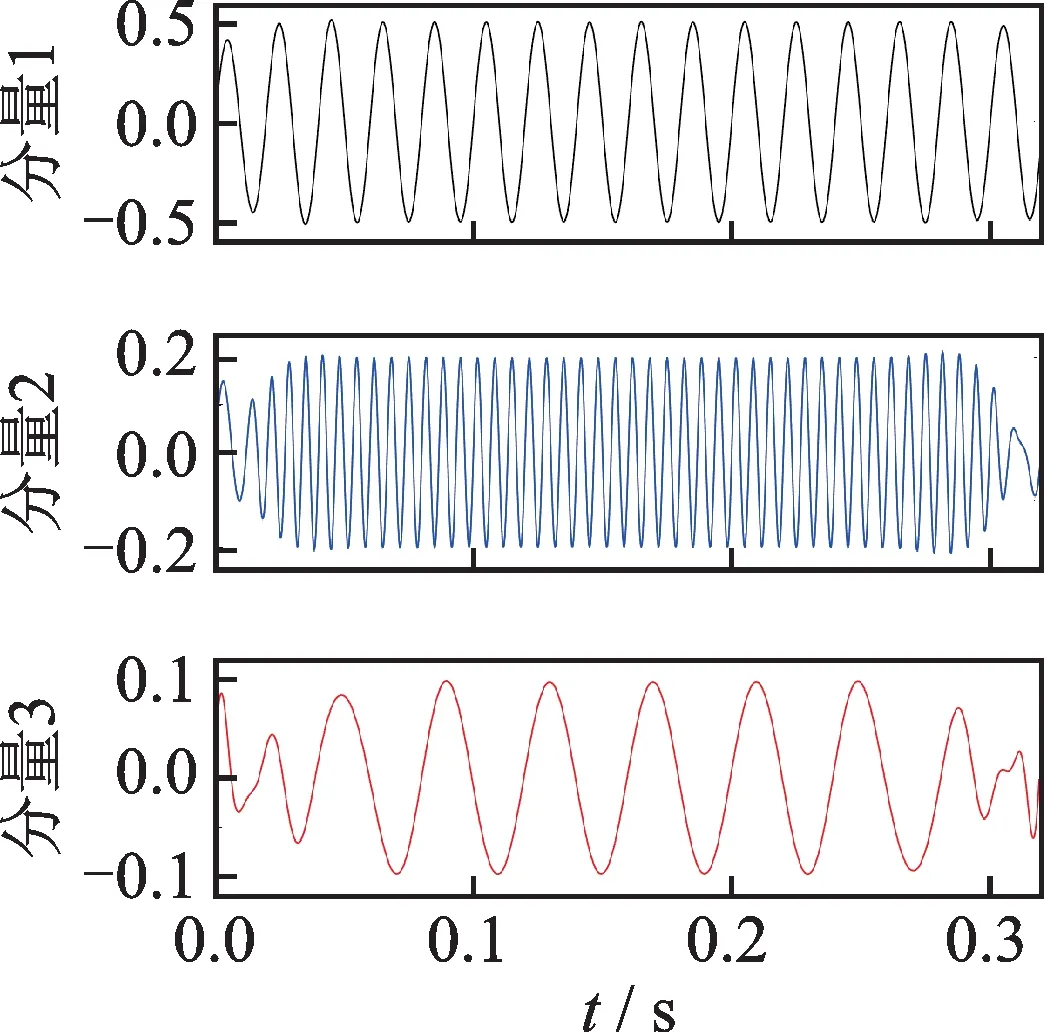
图2 HVD分解后的仿真信号Fig.2 Simulation signal after HVD decomposition

图3 HVD分解后的瞬时频率和瞬时幅值Fig.3 Instantaneous frequency and instantaneous amplitude after HVD decomposition
由此可知,仿真信号可以通过HVD进行分解,并正确地
提取出原信号的瞬时频率和瞬时幅值,从图3中可以看出波形的两端出现严重振荡,称为边界效应。
3 HVD算法的边界延拓
在HVD算法中由于Hilbert变换和低通滤波器对截断数据处理将会导致边界效应,输入信号两端出现无规则振荡,产生误差,且在迭代过程中误差会不断累积,影响当前分量的检测精度。因此,本文将采用自适应波形匹配延拓法解决这种边界效应[9-10]。
3.1 边界效应对检测精度的影响
本文选取电视机、冰箱、取暖器3个家用负荷的暂态事件来观察边界效应对检测精度的影响。图4为3个家用负荷的电流曲线图,由图可知电视机在6.1 s时切除,冰箱开始工作,到12 s时冰箱停止工作,取暖器投入使用。通过HVD算法分解出3个负荷的电流幅值曲线如图5所示。
图5为未经过边界延拓的负荷电流幅值曲线图,可明显看出各负荷在端点处出现不同程度的振荡,且随着迭代次数的增加,数据逐渐向中间传播,严重影响暂态事件的检测精度。
通过自适应波形匹配延拓法对负荷的电流幅值曲线进行边界延拓,如图6所示,对比发现各负荷在端点处的振荡明显减弱,两端的发散数据减少,边界效应有了明显的改善,这样能够大大地提升暂态事件的检测精度。

图4 3种负荷电流曲线图Fig.4 Three load current curves
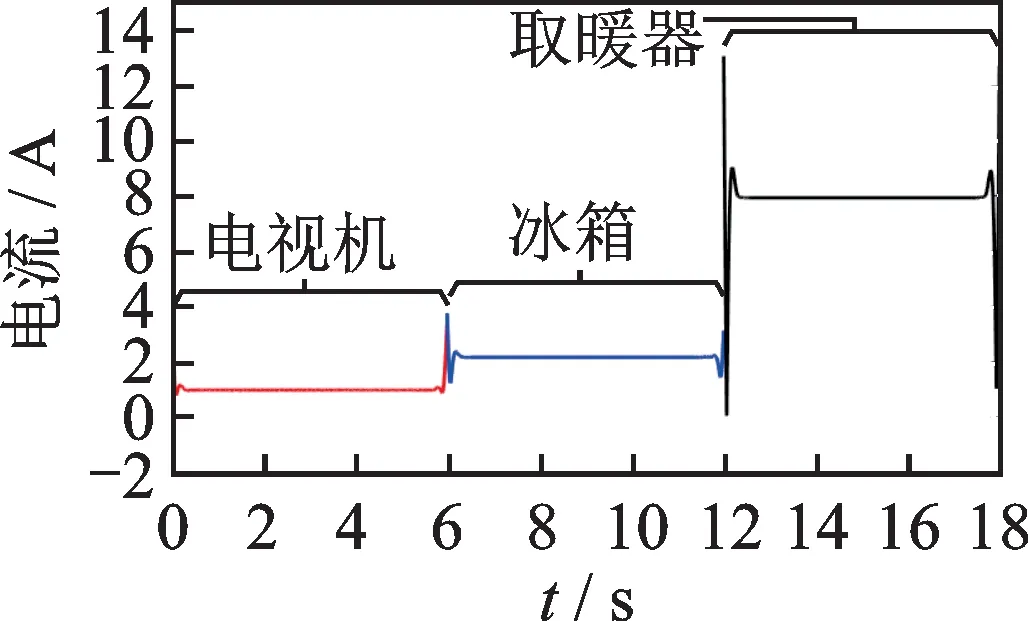
图5 负荷电流幅值曲线图Fig.5 Load current amplitude curve

图6 边界延拓后的负荷电流幅值曲线图Fig.6 Load current amplitude curve after boundary extension
3.2 单个电器事件检测的实验验证
通过MATLAB/Simulink软件搭建热水壶的电路模型,得出频率为50 Hz的电流曲线如图7所示和有功功率曲线如图8所示。由图可知,在2 s时电流和有功功率曲线产生第1个突变时刻,电流和有功功率同时增加,即热水壶启动工作;在8 s时电流和有功功率曲线突然下降产生第2个突变时刻,即热水壶关断停止工作。
图9为热水壶突变时刻定位监测,由图可知HVD算法可以精确地监测出热水壶的开启和关断时刻。
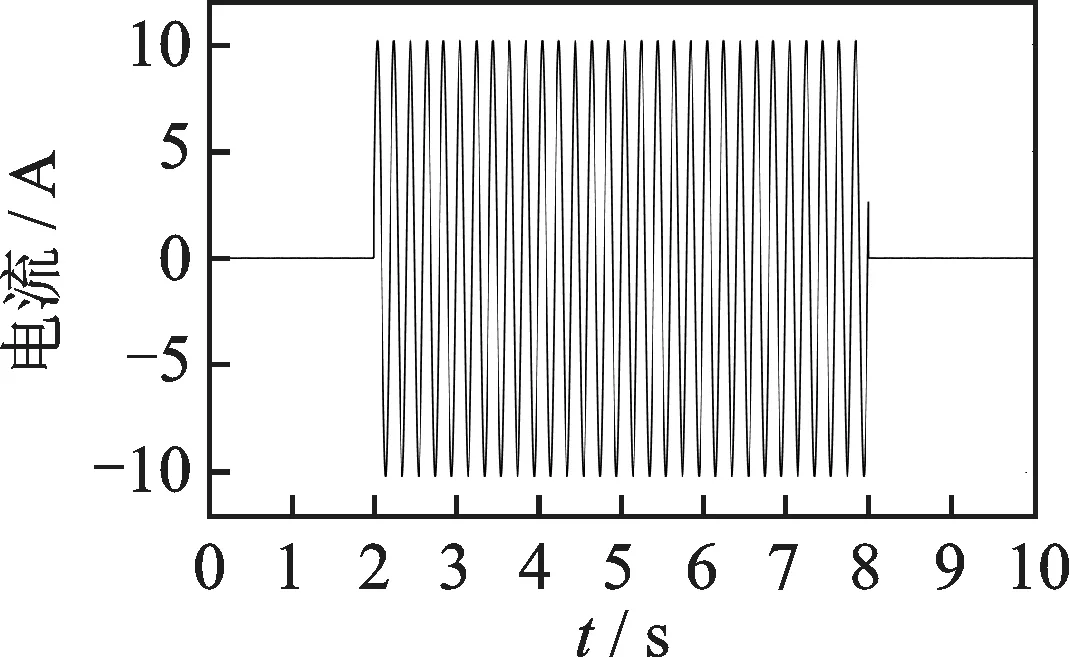
图7 热水壶的电流曲线Fig.7 Current curve of the kettle

图8 热水壶的有功功率曲线Fig.8 Active power curve of the kettle
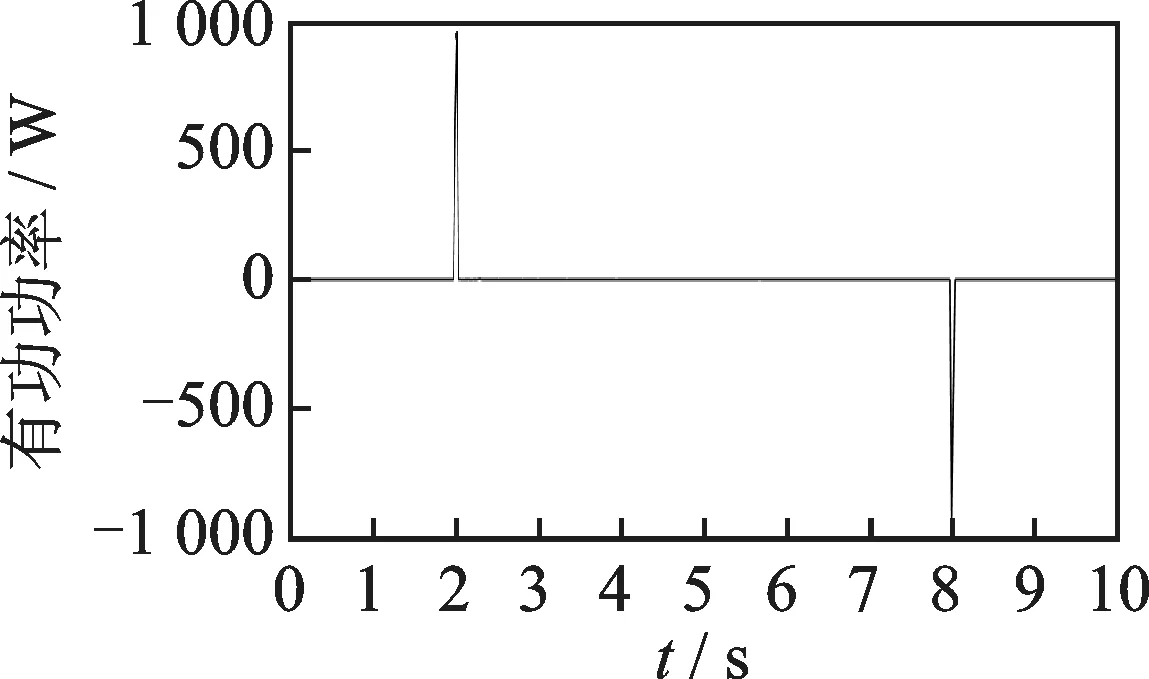
图9 热水壶突变时刻定位检测Fig.9 Kettle mutation moment location detection
4 算例分析
为了验证HVD算法对事件检测的准确性,本文对某用户中的电视机、热水器、取暖器、电风扇、微波炉、冰箱6种负荷的暂态事件进行检测。在MATLAB/Simulink软件中搭建模拟电路如图10所示,设额定电压为220 V,负荷的暂态事件结果用Scope以图像的形式输出。
首先设置对应的负荷动作序号与对应的暂态事件,如表1所示。运行Simulink仿真软件中的模拟电路,得到各个负荷的电流曲线如图11所示和所对应的有功功率曲线如图12所示,可以明显地看出负荷不同,切入的电流大小也不同,以及所对应的有功功率也各不相同。
在图12中纵坐标表示总负荷所处状态,且每一种状态所代表的情况对应唯一序号值,编号1~12对应于表1中序号所代表的总线负荷目前所处的状态。
由图13可知,当有暂态事件发生时,负荷的启动与关断分别代表着不同的纵坐标幅值,以0 W为分界线,上方为设备启动,下方为设备关断。
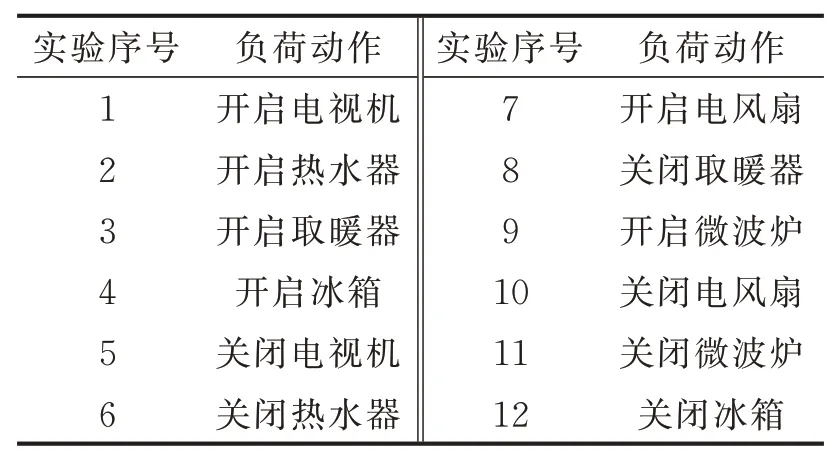
表1 负荷状态序号值Table 1 Load status number value
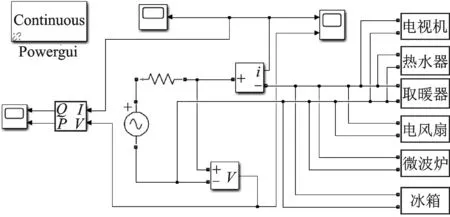
图10 仿真模型Fig.10 Simulation model
结合电流曲线图(图11)和有功功率曲线图(图12),以及对应负荷状态序号值可知,在2 s时电视机开始投入使用,电流值从0 A上升到2.5 A;2 s后热水器开启,电流值从2.5 A上升到4.9 A;6 s后取暖器开启,电流值从4.9 A上升到12.6 A;随后电冰箱、电风扇、微波炉开始投入使用,电流和有功功率发生了相应的变化。同时发现在15 s时,电流下降2.5 A,电视机处于关断状态;20 s时电流下降2.4 A,热水器处于关断状态,随后取暖器、电风扇、微波炉、冰箱处于关断状态。
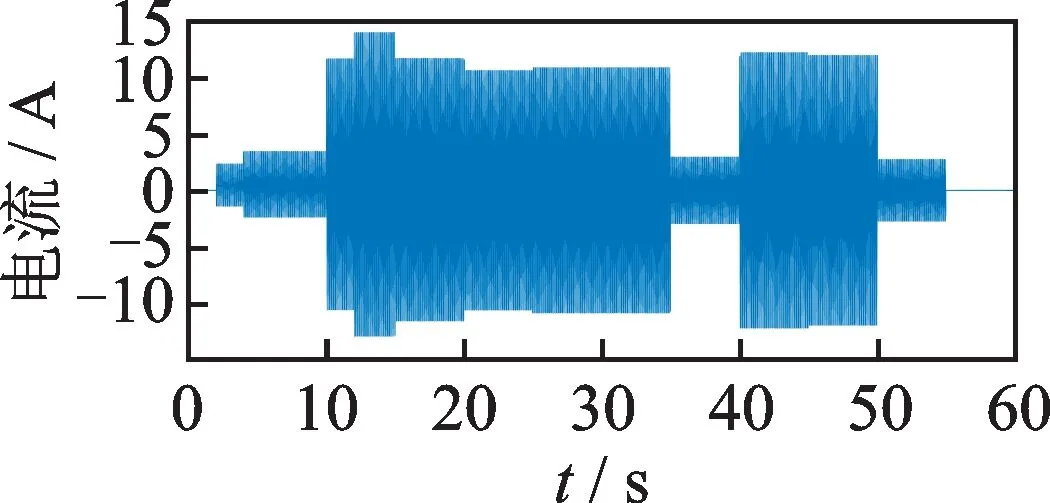
图11 6种负荷电流曲线图Fig.11 Six load current curves
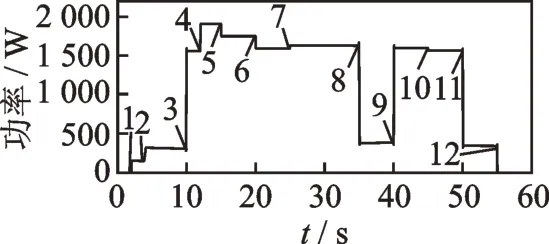
图12 负荷有功功率曲线图Fig.12 Load Active power curve
结合负荷状态序号值和图13得知,当负荷状态发生变化时暂态事件辨识结果图中所对应的各个负荷的状态都能及时有效地做出正确反应,即通过该算法可以有效地对暂态事件进行辨识。
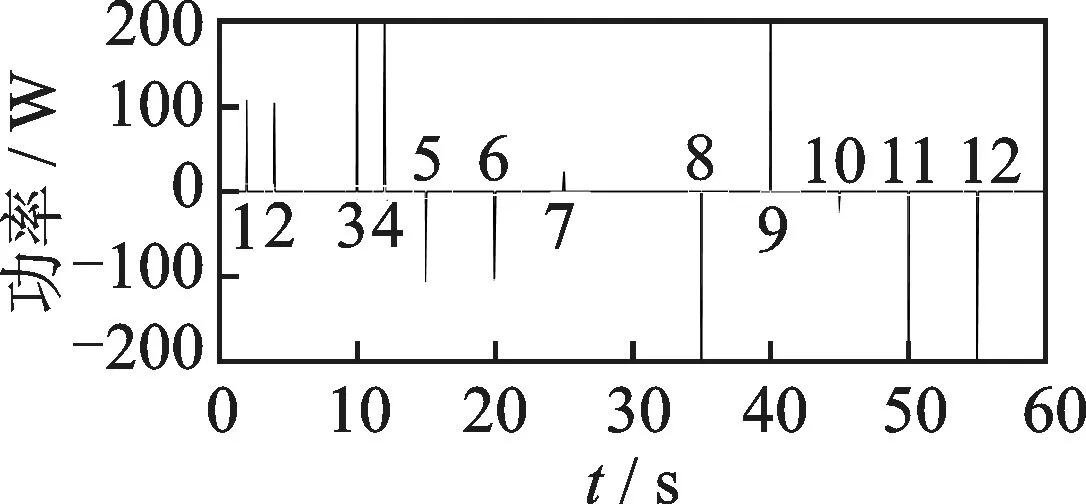
图13 暂态事件辨识结果图Fig.13 Graph of transient event identification result
5 结束语
在智能用电的趋势下,为了帮助用电用户更为详细地了解各个时段的用电情况,做到合理用电,减少电费开支,节约能源,本文提出了基于HVD算法的负荷暂态事件监测方法,通过对某用户的6种电器设备的暂态事件进行监测,并利用MATLAB/Simulink仿真软件搭建了对应的模拟电路。总结得出:该算法可以准确地监测出用电负荷的投入与切除时刻,较好地验证暂态事件辨识的有效性和可行性。电力公司可以根据该方案了解各个区域的用电信息,合理定价,提高电网利用率,减少投资,降低用户的停电概率。

