基于SVM模型算法和大数据分析技术的船舶设备故障诊断

王晓东， 马旭颖

(上海船舶运输科学研究所 舰船自动化系统事业部，上海 200135)

0 引 言

相比互联网等新兴行业，船舶行业在大数据与人工智能(Artificial Intelligence，AI)的结合应用方面起步较晚，所做的工作相对滞后。船舶行业涉及到很多业务，包括船舶设计、船舶建造和货物运输等，因此蕴含有大量有价值的数据信息。将大数据分析技术应用到船舶行业中，不仅能节省船舶运输成本，而且能更好地对船舶设备进行故障诊断[1]，大大提升船舶的运行效率。

本文以船舶柴油机的故障诊断为例，研究将大数据分析方法和支持向量机(Support Vector Machine，SVM)模型算法应用到柴油机故障诊断中的可行性，为船舶行业提供一种基于大数据分析的船舶设备故障诊断方法。

1 大数据分析技术在船舶行业中的应用

随着社会的不断发展、科技的不断进步，大数据分析技术越来越成熟，已广泛应用到很多行业中。在船舶行业，目前已有很多船企和船舶组织将大数据分析技术应用到其实际业务中，取得了良好的效果。

1)航行中的船舶能不间断地采集其主要设备的运行数据，通过对这些数据进行分析，判断主要设备的运行状态，在此基础上，根据主要设备的运行数据要求预测其故障发生概率，从而提前采取设备维护措施，为设备的正常运行提供保障。

2)船企通过对船舶航行数据进行采集、分析和预测，获得船舶的主机功率、航速、航行过程中的能耗、各船用设备的运行状态和航行区域的海况等数据。通过对这些数据进行分析，了解海况对航速、航行能效、主机功率和各类设备的运行状态的影响。

3)应用大数据分析技术能得到准确测量和预测清理水下船体和螺旋桨表面附着物的最佳时间，并进一步分析出船底污物与船舶航行时间和航线之间的关系，结合进坞维修时测算的清污成本就可预测出能使成本最低的进坞维修、清污时间节点。

4)应用大数据分析技术能大大提高船舶节能减排的效率。船企能通过基于大数据分析技术的船舶航行能源需求预测系统监控船位、柴油发动机能耗和转速等数据，实现对船舶燃油情况的实时远程监测。同时，能通过实时采集数据并进行大数据分析，根据柴油机油耗量、船舶排水量和航速之间的关系，对船舶能耗策略进行优化，得到一个能指导船舶运行在最佳工作点上的能耗指标，实现船舶能耗最少的目标。

5)应用大数据分析技术可对船舶设备进行故障诊断。通过采集船舶设备的重要参数,如柴油机转速、柴油机功率和柴油机滑油压力等，并应用大数据分析技术分析、预测船舶设备的故障发生概率，达到及时消除故障和预测故障发生的目标，大大提高船舶航行的安全性和可靠性。

2 SVM模型算法

SVM属于有监督的机器学习算法，可用于对离散因变量进行分类和对连续因变量进行预测，能将低维度的线性不可分的空间转换为高维度的线性可分的空间。该算法的核心思想是利用某些支持向量构成的“超平面”，对不同类别的样本点进行划分(见图1)。该模型算法的优点有：

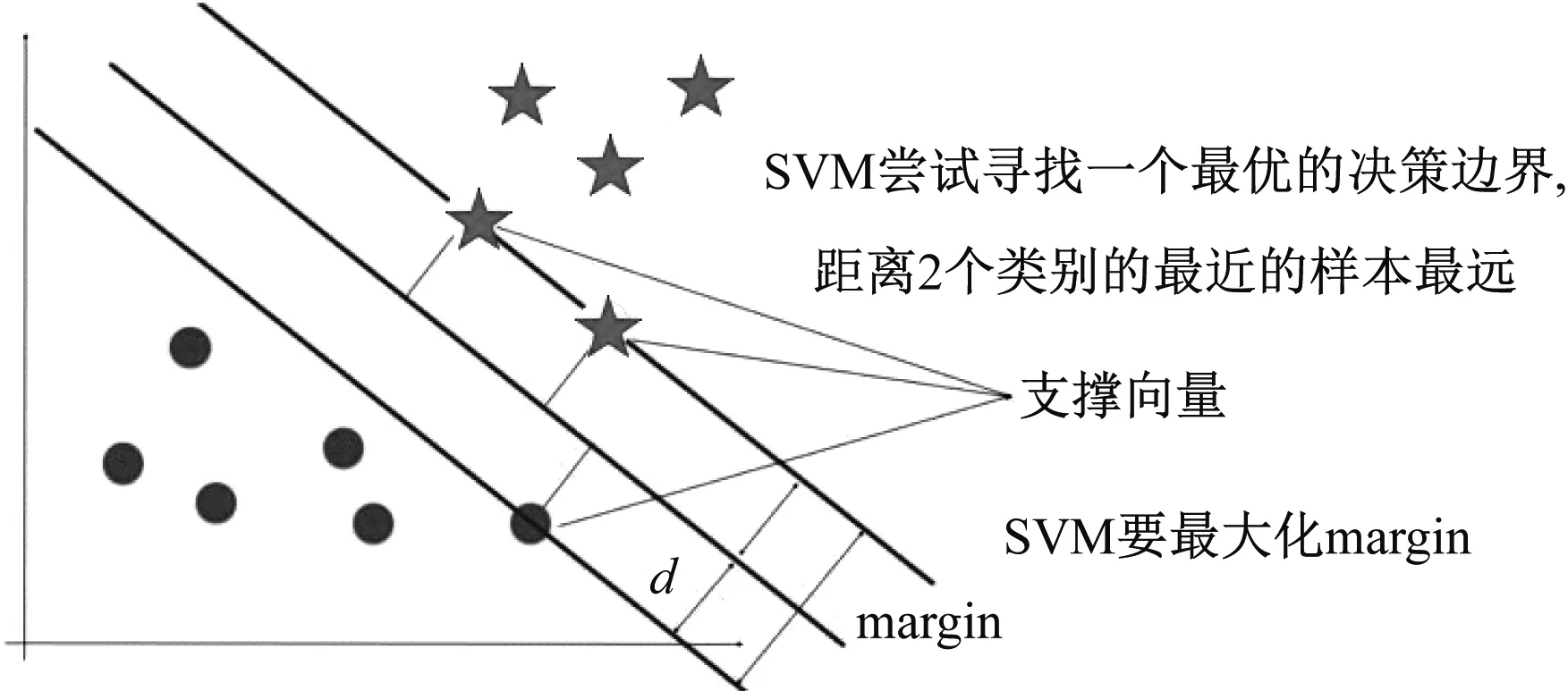
图1 SVM算法核心思想示意

1)有很好的鲁棒性，能避免“维度灾难”的发生(模型计算的复杂度不会随数据维度的增多而提高)；

2)有很好的泛化能力，能避免模型过拟合；

3)能避免模型在运算过程中出现局部最优。

SVM模型算法分为线性可分模型算法和非线性模型算法2种，其中线性可分的SVM模型示意见图2。

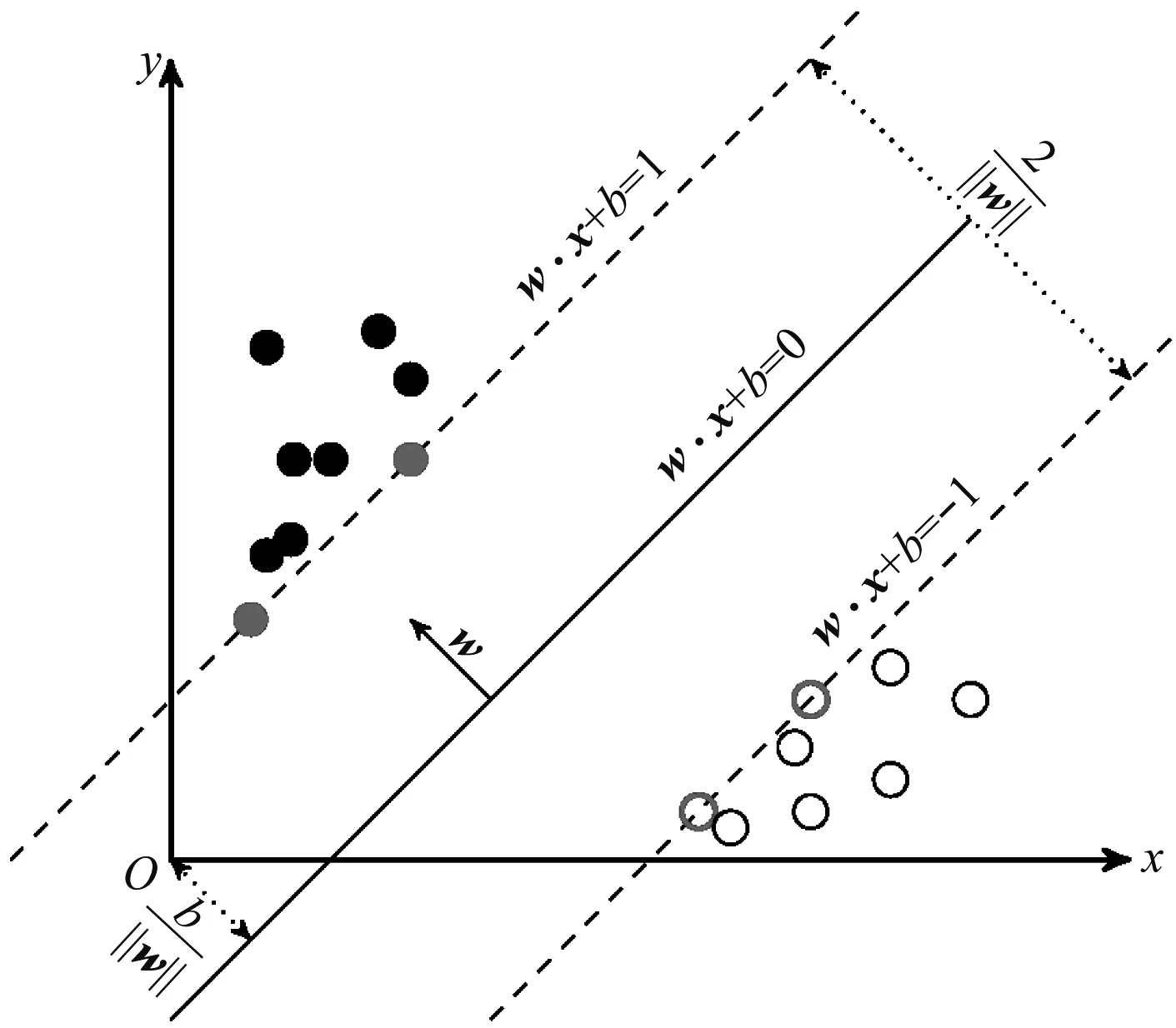
图2 线性可分的SVM模型示意

通过推导得出SVM线性可分模型算法的目标函数[2]为

(1)

(2)

αi≥0

(3)

式(1)～式(3)中：xi为样本点；yi为样本点所属的类别；αi为拉格朗日乘子；(xi·xj)为2个样本点的内积。计算分割面w′x+b=0的参数w和b[2]，有

(4)

(5)

当遇到样本点线性不可分的情况(见图3)时，解决方法是将二维线性不可分样本映射到高维空间中，使样本点在高维空间中线性可分(见图4)。

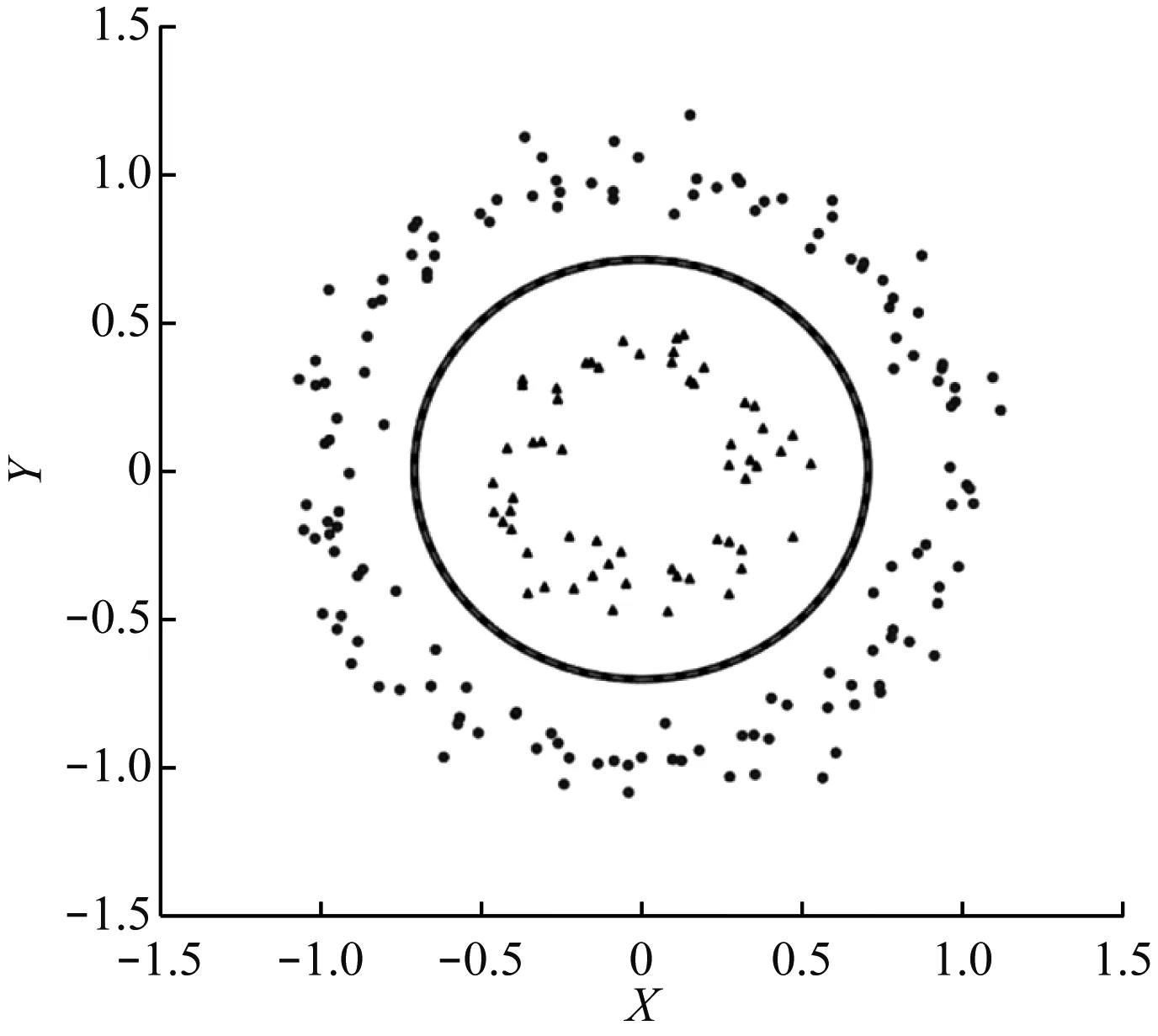
图3 线性不可分样本示意

图4 二维样本映射到高维空间示意

通过推导得出SVM非线性模型算法的目标函数[2]为

(6)

(7)

0≤αi≤C

(8)

式(6)～式(8)中：内积φ(xi)·φ(xj)可利用核函数替换，即K(xi·xj)=φ(xi)·φ(xj);C为惩罚系数值，默认为1。推导出线性“超平面”参数w和b的值[2]为

(9)

(10)

核函数可选择线性核函数、多项式核函数、高斯核函数和Sigmoid核函数等。以高斯核函数为例，其表达式为

(11)

故对应的分割“超平面”为

(12)

式(11)和式(12)中：γ为高斯核函数的参数[2]。

3 船舶设备故障诊断

船舶柴油机是船舶动力装置的核心设备，下面以该设备为例进行船舶设备故障诊断分析。若该设备频繁发生故障，会影响船舶的正常航行，因此保证船舶柴油机正常工作非常重要。船舶柴油机滑油系统是船舶柴油机中最重要的系统，其作用是通过润滑油保证柴油机的零件表面润滑，以减小其摩擦阻力和零件间的磨损，并带走摩擦产生的热量和磨损产物，同时具有防腐、传递动力和减轻噪声等作用。若柴油机滑油系统出现故障，会导致柴油机降速运行,甚至停止运行，造成重大事故[3]。

船舶柴油机长时间工作之后，受机器振动和机器零件磨损、疲劳等因素的影响，其滑油系统可能会发生故障。例如，某油船在长时间航行之后，其柴油机滑油系统油泵出口压力突然从0.42 MPa降到0.23 MPa，造成柴油机主机降速，险些引发重大事故。经过排查得知，该问题是第四缸曲柄箱内零件断裂导致的[3]。

通过分析可知，船舶柴油机各工况的运行时间和超过主机额定功率的运行时间等因素与柴油机零件的磨损和疲劳存在对应关系，因此也与柴油机滑油压力低的故障存在对应关系[4]。由此，可采用SVM模型算法分析船舶柴油机滑油压力低的故障与船舶柴油机各工况的运行时间和超过主机额定功率的运行时间等因素之间的关系。通过采集船舶航行数据，采用SVM模型算法对“柴油机滑油压力低”这个故障点进行预测。

4 柴油机滑油压力低故障预测

Python语言属于解释型脚本语言，具有简洁、易读和可扩展等特点，广泛应用于科学计算、大数据统计、AI、软件开发和网络爬虫等领域中。本文采用Python语言编写程序，结合其自带的sklearn机器学习模块，实现SVM模型算法的实际应用。

采用某船6个月的航行数据进行大数据分析，这些数据为船舶每天航行之后保存的数据，包括各工况的运行时间、超过主机额定功率运行时间和柴油机滑油压力低故障报警等。

1)采集数据之后，需对这些数据进行清洗，包括查看数据集中是否存在数据缺失问题、数据是否具有完整性和一致性、数据中是否存在异常值等。当数据集中存在数据缺失问题时，采用替换法，用均值替换缺失值；当数据集中存在异常数据(即远离正常值的数值)时，采用删除法删除这些异常数据。

2)对数据进行转化处理，将每天各工况的运行时间数据转化为2次柴油机滑油压力低故障报警之间的时间数据，每当出现新的报警时，就将运行时间数据从0开始累加；对柴油机滑油压力低故障进行归一化处理，报警数据转化为1，正常数据转化为0。数据采集点对应变量见表1。将柴油机滑油压力低故障作为特征值。

表1 数据采集点对应变量

3)采用Python语言对数据进行训练集和测试集拆分，同时采用网格搜索法选择最佳惩罚系数C，采用SVM模型对训练集数据进行训练，训练之后在测试集中进行测试。

4)对比SVM线性模型算法与SVM非线性模型算法的测试结果。选择2个模型中训练效果更好、满足数据拟合要求的模型作为该船的SVM模型。

采用SVM模型算法的工作流程见图5。

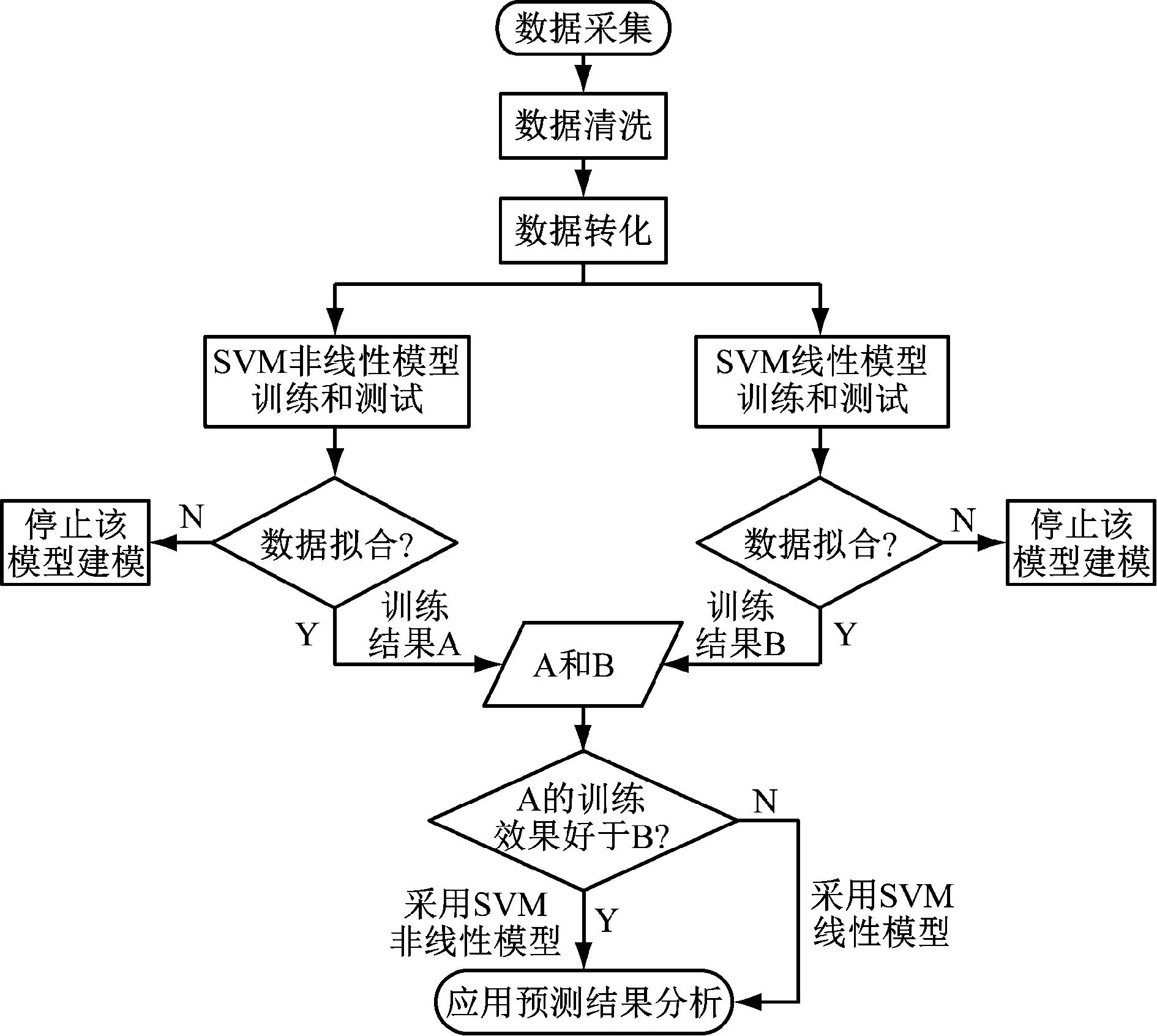
图5 采用SVM模型算法的工作流程

首先采用SVM线性模型算法建模，采用Python语言编写的代码如下：

1. from sklearn import svm

2. import pandas as pd

3. from sklearn import mdel_selection

4. datas=pd.read_csv(r'C:UsersNeighborWangDesktopDatas.csv')

5. predatas=datas.columns[1:]

6. x_trainSVM,x_testSVM,y_trainSVM,y_testSVM=model_selection.train_test_split(datas[predatas],datas.柴油机滑油压力报警,test_size=0.25,random_state=1234)

7. C=[0.05,0.1,0.5,1,2,5]

8. paramSVM={'C':C}

9. model_linear_svc=model_selection.GridSearchCV(estimator=svm.LinearSVC(),param_grid=paramSVM,scoring='accuracy',cv=5,verbose=1)

10. model_linear_svc.fit(x_trainSVM,y_trainSVM)

11. model_linear_svc.best_params_,model_linear_svc.best_score_

12. Out[11]: #输出结果

13. ({'C': 5}, 0.9259259259259259)

14. preModel_linear_svc=model_linear_svc.predict(x_testSVM)

15. metrics.accuracy_score(y_testSVM,preModel_linear_svc)

16. Out[13]: #输出结果

17. 0.7333333333333333

采用网格搜索法5重交叉验证之后，发现SVM线性模型最佳的惩罚系数C=5，虽然该模型在训练数据集上的平均预测准确率有92.5%，但其在测试数据集上的预测准确率只有73.3%，说明存在过拟合现象，故SVM线性可分模型并不适合在该数据集上应用。

随后采用SVM非线性模型算法重新建模，采用Python语言编写的代码如下：

1. kernelSVM=['rbf','linear','poly','sigmoid']

2. C1=[0.1,0.5,1,2,5]

3. paramSVM1={‘kernel’:kernelSVM,'C':C1}

4. model_svc=model_selection.GridSearchCV(estimator=svm.SVC(),param_grid=paramSVM1,scoring='accuracy',cv=5,verbose=1)

5. model_svc.fit(x_trainSVM,y_trainSVM)

6. model_svc.best_params_,model_svc.best_score_

7. Out[24]: #输出结果

8. ({'C': 0.1, 'kernel': 'rbf'}, 0.9703703703703703)

9. preModel_svc=model_svc.predict(x_testSVM)

10. metrics.accuracy_score(y_testSVM,preModel_svc)

11. Out[25]: #输出结果

12. 0.9333333333333333

采用网格搜索法5重交叉验证之后，发现模型最佳的惩罚系数C=0.1，最佳的核函数kernel为'rbf'，即径向基核函数。相比SVM线性可分模型，基于核技术的SVM非线性模型表现出了极佳的应用效果。模型在训练数据集上的平均预测准确率为97%，在测试数据集上的预测准确率也有93.3%，说明采用SVM非线性模型拟合和预测该样本数据集是十分有效的，故可采用SVM非线性模型预测船舶柴油机滑油压力低故障的发生概率。例如，将采集到的当前变量数据输入到SVM非线性模型预测函数中，得到预测结果。若预测结果是0，则表示大概率不会发生故障；若预测结果是1，则表示极大概率会发生故障。对该过程采用Python语言编写的代码如下：

1. #采集到的变量X1-X6的数据为[138,174,258,618,594,54]

2. X_In=[138,174,258,618,594,54]

3. #将采集到的变量输入预测函数中

4. pre_result=grid_svc.predict([X_In])

5. #输出预测结果

6. print(pre_result)

7. #结果为0,即不会产生故障

8. [0]

当模型提供的预测结果是会发生故障时，提前对柴油机滑油系统进行机械和管路检查，避免发生滑油压力低的故障，这样就能大大提高船舶航行的安全性和经济效益。

5 结 语

本文采用SVM模型算法，利用大数据分析了船舶柴油机滑油压力低故障的发生概率。模型运算结果表明，该模型在训练数据集和测试数据集上的准确率都较高，对提前预测柴油机滑油压力低的故障有很大作用。但是，本文分析的数据集属于小规模数据集，存在数据过拟合的可能性，故该模型只适合特定的船舶，不能直接用来对其他船舶进行预测，若要使其适用其他船舶，还需重新采集数据。