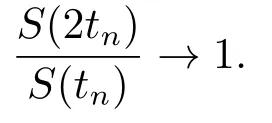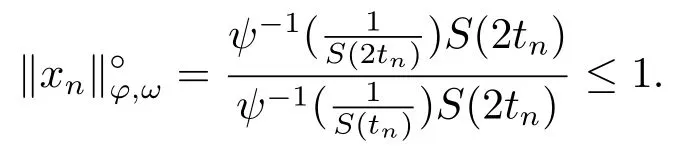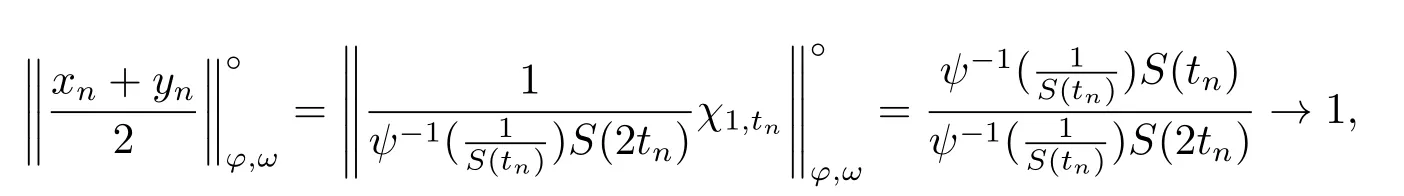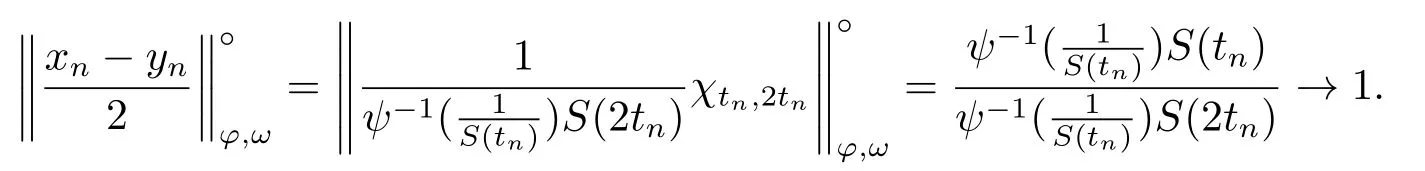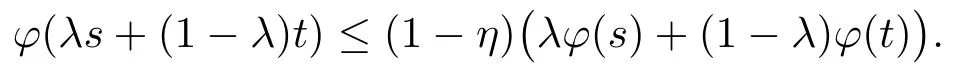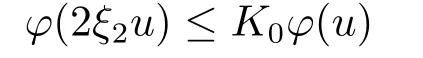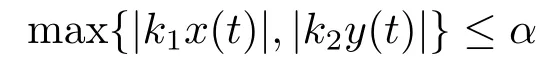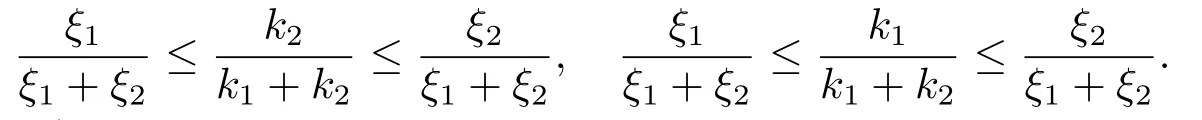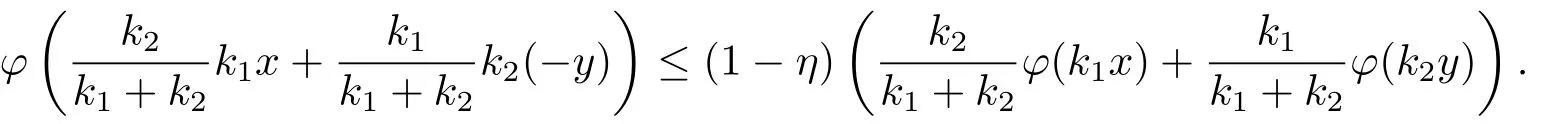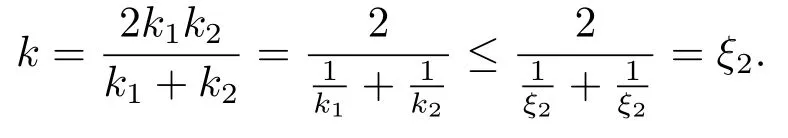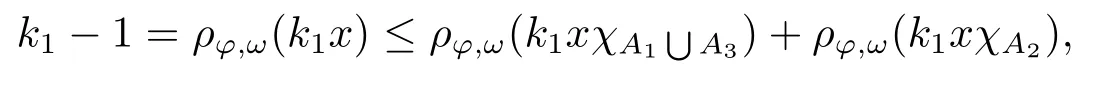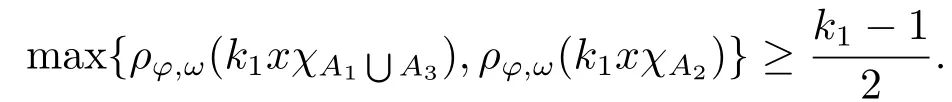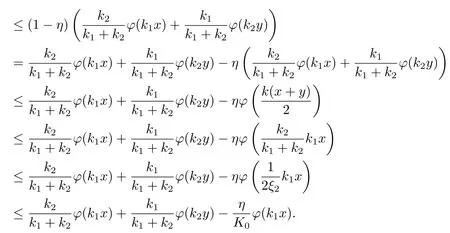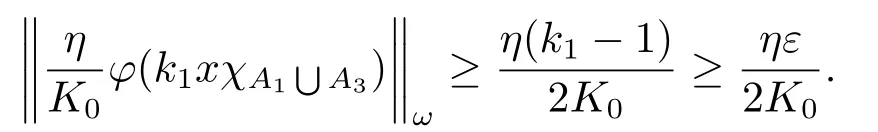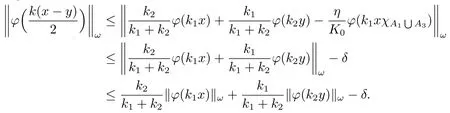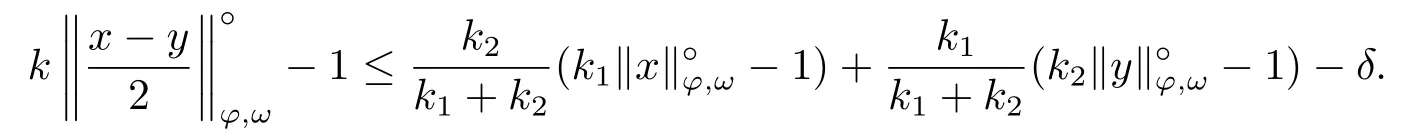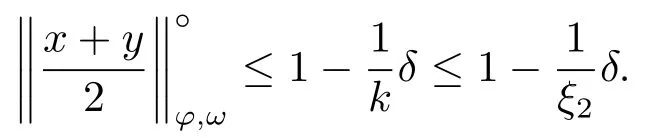Uniformly Normal Structure and Uniform Non-Squareness of Orlicz-Lorentz Sequence Spaces Endowed with the Orlicz Norm
CHEN Bowen(陈博文),GONG Wanzhong(巩万中)
(Department of Mathematics,Anhui Normal University,Wuhu 241000,China)
Abstract: As a generalization of classical Orlicz space,Orlicz-Lorentz space provides a reasonable space framework for harmonic analysis and differential equations.While uniformly normal structure and uniform non-squareness play important roles in fixed point theory.In this paper the necessary and sufficient conditions were given for Orlicz-Lorentz sequence space endowed with the Orlicz norm having uniformly normal structure and uniform non-squareness.
Key words: Uniformly normal structure;Uniform non-squareness;Orlicz-Lorentz sequence spaces;Orlicz norm
1.Introduction
LetAbe a bounded subset of a Banach spaceX,forx ∈Awe set
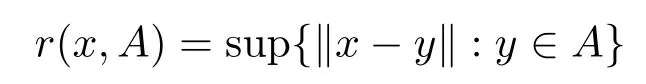
and set
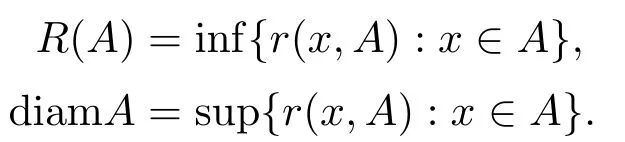
Xis said to have normal structure if eitherR(A)= 0 orR(A) For anyx,y ∈S(X),if there existsδ ∈(0,1)such that we say that Banach spaceXis uniformly non-square[13].Uniform non-squareness of Banach spaces has been defined by James as the geometric property which implies super-reflexivity[14].Recently García-Falset,Llorens-Fuster et al.[9]have shown that uniformly non-square Banach spaces have the fixed point property.Recently Foralewski et al.[7−8]got the criterion for Orlicz-Lorentz function space and Orlicz-Lorentz sequence space with the Luxemburg norm being uniformly non-square. A functionφ:R→R+is said to be an Orlicz function[16]ifφis convex,even,φ(0)=0,φ(u)>0 for allu >0,Its complementary functionψis defined by for allv ∈R.Ifφis an Orlicz function,then its complementary functionψis an Orlicz function.Recall that an Orlicz functionφsatisfies the conditionδ2(φ ∈δ2for short)if there exists a constantK >0 and a constantu0>0 such thatφ(2u)≤Kφ(u)wheneveru ∈[0,u0].From[21]we know that ifφ,ψ ∈δ2,then for anyα>0 andthere exists 0 For more properties of Orlicz function,we may refer to [6,11,16]. Letl0be the space of all sequencesx:N→(−∞,∞).Give anyx ∈l0,the distribution function and decreasing rearrangement ofxare defined as follows whereµdenotes the counting measure on N.A weight sequenceω= (ω(t))is nonincreasing sequence of positive real numbers such thatA weight sequence is said to be regular if there existsK >1 such that for anyn ∈N,where The Orlicz-Lorentz sequence spaceλφ,ωis defined as the set of the sequencesx=(x(t))such that for someλ >0.It is known that the Orlicz-Lorentz sequence space endowed with the Luxemburg norm is a Banach space[20].Ifφ(t)=t,thenλφ,ωis the Lorentz sequence spaceλω.The norm ofx ∈λωis defined by Obviously, We say that a Banach latticeXis uniformly monotone if for anyε >0 there isδ=δ(ε)>0 such that∥u −v∥≤1−δwheneveru,v ∈Xwith∥v∥>ε,∥u∥=1 and 0≤v ≤u.From [12] we see thatλωis uniformly monotone if and only ifωis regular. Forx ∈λφ,ω,define It is easy to see that∥·∥◦φ,ωis a norm inλφ,ω,we call it Orlicz norm.From [20],we know that endowed with the Orlicz norm,λφ,ωis a Banach space(denoted byλ◦φ,ω),and obtain the following properties ofλ◦φ,ω. wherek∗=inf{h>0:ρψ,ω(p(h|x|))≥1},k∗∗=sup{h>0:ρψ,ω(p(h|x|))≤1}. In this paper we will firstly give the criterion forλ◦φ,ωhaving uniformly normal structure,then give the necessary and sufficient conditions forλ◦φ,ωbeing uniformly non-square.In the proof uniformly monotonicity plays an important role.For more reference about uniformly normal structure and uniform non-squareness,we may refer to [18]. Lemma 2.1[20](i)inf{k:k ∈K(x),∥x∥◦φ,ω=1}>1 if and only ifφ ∈δ2. (ii)The setQ=∪{K(x):a ≤∥x∥◦φ,ω ≤b}is bounded for eachb ≥a>0 if and only ifψ ∈δ2. Lemma 2.2[20] Lemma 2.3Ifφ /∈δ2,thenλ◦φ,ωcontains an almost isometric copy ofℓ∞. ProofSinceφ /∈δ2,for anyε>0,we can find decreasing sequence of positive numbers{un}such that for anyn ∈N.Then there exists a sequence{k(n)}of natural numbers such that for anyn ∈N.Denotel(0)=0,and Obviously there holds For anyc={cn}∈ℓ∞,we have For anyr >1,we can get onemsuch thatand get oneslarge enough satisfyingandε2s >2m+1.Therefore Consequently,we can get Lemma 2.4Ifψ /∈δ2,thenλ◦φ,ωcontainsℓ1. ProofFor anyε>0,byψ /∈δ2there is a sequence{ui}of positive numbers such that and for alli ∈N.In view ofwe can get a sequenceof natural numbers satisfying Definel(0)=0 andfori ∈N.We have fori=2,3,···.It is easy to see thatk(i)>2i+3k(i −1)andk(i)>l(i −1). Define Then by the same method as the proof of Theorem 2.5 in[8],we know that the sequence{xi}satisfies In view of the properties of the Orlicz norm,we obtain Consequently, Lemma 2.5Ifωis not regular,thenλ◦φ,ωcontainsℓn∞uniformly. ProofSinceωis not regular,we see that for anynand anyε ∈(0,1),there exists a nature numberα>1 such that Fora={ak}nk=1∈ℓn∞with max{|ak|:k= 1,···n}= 1,we may assume|a1|= 1.By the inequality above and the relations between the Luxemburg norm and the Orlicz norm, It follows thatλ◦φ,ωcontainingℓn∞uniformly. Lemma 2.6[1,17]LetXbe a Banach space.IfXhas uniformly normal structure,thenXis reflexive and it does not containℓn∞uniformly. Owing to the definition of uniformly normal structure,we have Lemma 2.7[6]LetXbe a Banach space.IfXdoes not have uniformly normal structure,then for anyn ∈N andε>0,there exists{xi:1≤i ≤n+1}inXsuch that Theorem 3.1Orlicz-Lorentz sequence spaceλ◦φ,ωhas uniformly normal structure if and only if (a)ωis regular, (b)φ,ψ ∈δ2. Proof(Necessity)It follows from Lemmas 2.3-2.6,Lemma 2.4,Lemma 2.5 and Lemma 2.6. (Sufficiency)By Lemma 2.1 andφ,ψ ∈δ2,we see that there existξ1,ξ2∈(1,+∞)withξ1<ξ2such thatkx ∈(ξ1,ξ2)for anyx ∈λ◦φ,ωwith For anyx ∈λ◦φ,ωwith∥x∥◦φ,ω ≤1,we know thatCertainlyandx∗(1)=max{|x(t)|,t ∈N}.Fix Byφ,ψ ∈δ2,forandα >0 above,there existc ∈(0,1)andγ >0 such that,whenλ ∈(λ0,1−λ0)and max{|s|,|t|}≤α, In view ofωbeing regular,we know thatλωis uniformly monotone.Thus for anyM >0 and anyε1>0,there existsη(ε1)>0 such that for anyu,v ∈λω,∥u∥w ≤M,|v|≤|u|and∥v∥ω ≥ε1. Consideringφ ∈δ2,there existandK0>1 such that whenever∥u∥φ,ω ≥1−ε2andφ(2r)≤K0φ(r)whenever Suppose thatλ◦φ,ωdoes not have uniformly normal structure,then fornabove and anyε ∈(0,ε2)there exists a subset{x1,··· ,xn}⊂λ◦φ,ωsatisfying Without loss of generality,we may assume thatx1= 0 andx2≥0.In fact,ifx10,then we will replacexibyxi −x1fori=1,2,...n.And we will replacexi(t)by−xi(t)fort ∈N withx2(t)<0,wherei=2,3,...n.Certainlyfori=2,3,··· ,n.There is a mappingσ:N→N such that From∥x2∥◦φ,ω ≥1−ε,we can see∥2x2∥φ,ω ≥1−ε.Therefore whereA:={t ∈N:x2(t)≥α0}.For 2 Let Bi={t ∈A:Inequality (3.2)is true for anyk Using the same method as Theorem 6 of[15],we can see that there exists ai0∈{2,··· ,n}such that Let wherehk ∈K(xi0−xk)andk ∈{1,2,··· ,i0−1}.By∥xi0−xk∥◦φ,ω ≤1,we can find that and Ifhi0−1≥hk,we can see Clearly we can get the same result ifhi0−1≤hk.Consequently,byφ,ψ ∈δ2we know that fort ∈Bi0, For 3≤j ≤i0,let Hence,by the convexity ofφ,we can get But by (3.3), Therefore, for someη(ε1)>0.It can be obtained By (3.1)and(3.4),we have which leads to a contradiction by the arbitrariness ofε.Soλ◦φ,ωhave uniformly normal structure. Theorem 4.1Orlicz-Lorentz sequence spaceλ◦φ,ωis uniformly non-square if and only if (a)ωis regular, (b)φ,ψ ∈δ2. Proof(Necessity)By Lemmas 2.3-2.4,we can seeφ ∈δ2andψ ∈δ2.Supposeωis not regular,then we can find an infinite sequence{tn}⊂N such that Let By Lemma 2.2 andtn ≤2tn,we know While byx∗n=y∗n,there hold and A contradiction with the uniform non-squareness yields the regularity ofω. (Sufficiency)By Lemma 2.1 andφ,ψ ∈δ2,we see that there existξ1,ξ2∈(1,+∞)withξ1<ξ2such thatku ∈(ξ1,ξ2)for anyu ∈S(λ◦φ,ω). Letx,y ∈S(λ◦φ,ω).Obviously,soBy condition (b),forandthere existc ∈(0,1)andη >0 such that whenλ0≤λ ≤1−λ0and max{|s|,|t|} ≤α,for eitherorst ≤0,it holds In view ofφ ∈δ2,there existsK0>1 such that for|u|≤2(ξ2)2α. Fixk1∈K(x),k2∈K(y),then fort=1,2,···and Therefore,ifx(−y)≤0,we have By the definition of the Orlicz norm and∥x∥◦φ,ω=∥y∥◦φ,ω=1,one can see Setε=ξ1−1 andBy the range ofk1andk2,we find Denote Since we have On the other hand, Hence by the uniform monotonicity of Lorentz sequence spaceλω,there exists a0 satisfying By the definition of∥·∥ωand the Orlicz norm,we have Consequently, In summary,λ◦φ,ωis uniformly non-square.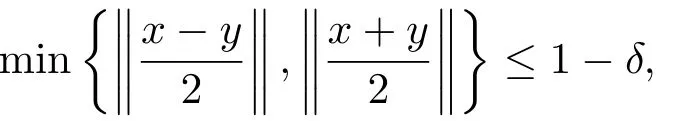
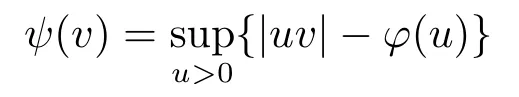
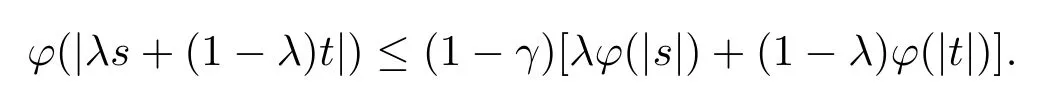
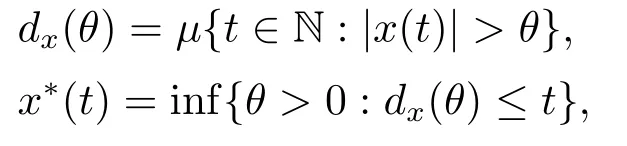
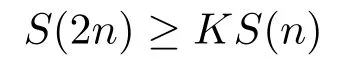
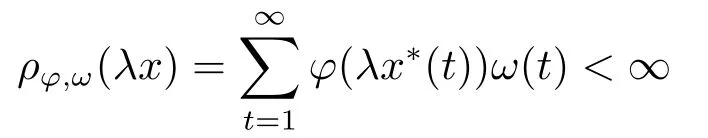
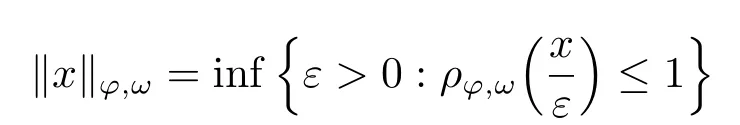
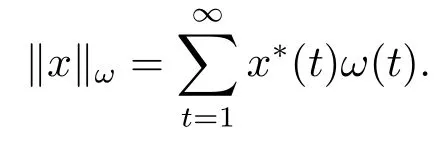
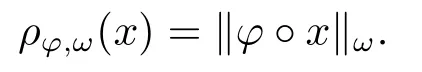
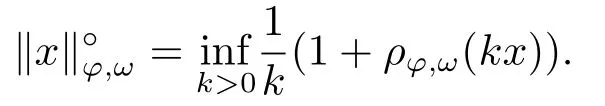
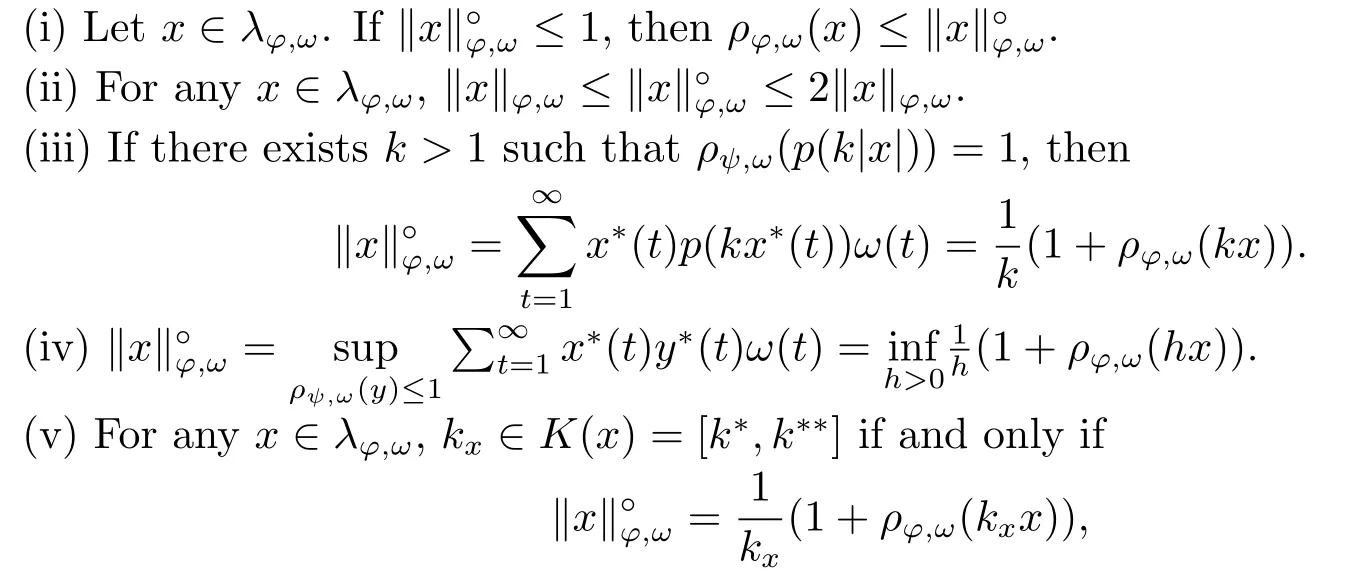
2.Some Lemmas
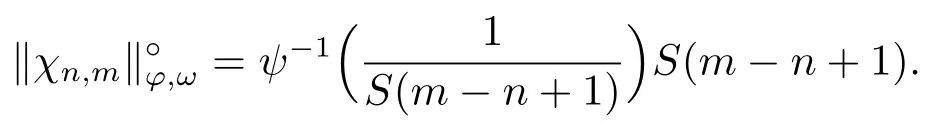
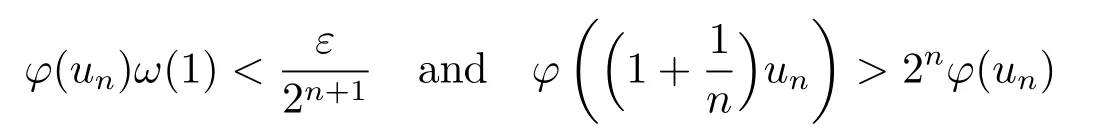

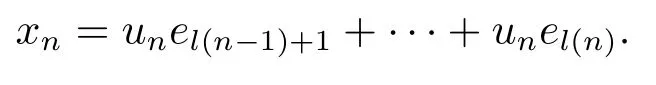
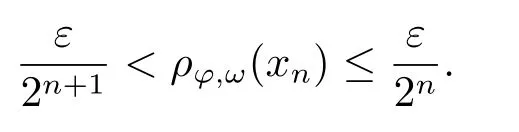
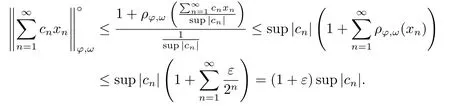
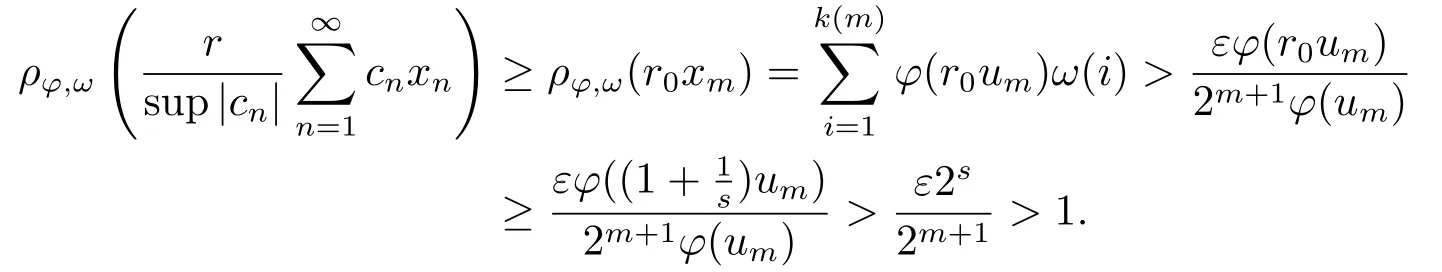
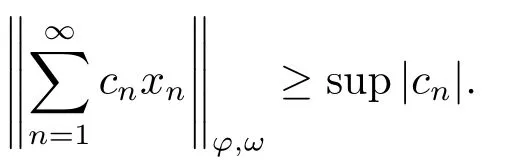
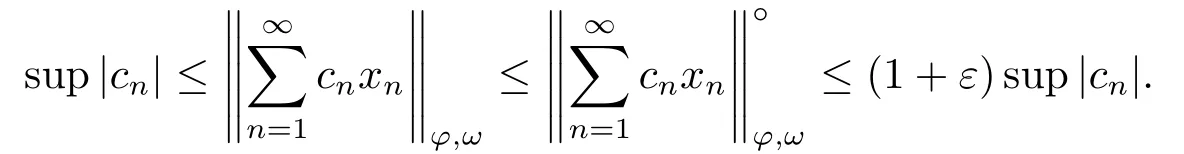
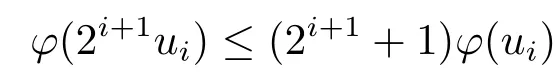
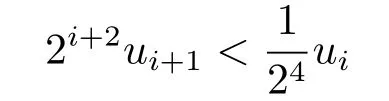
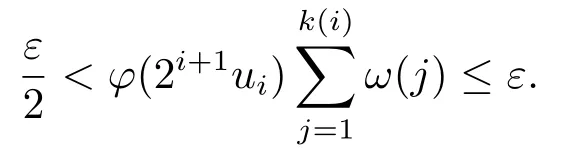
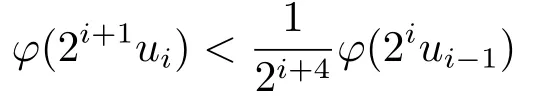
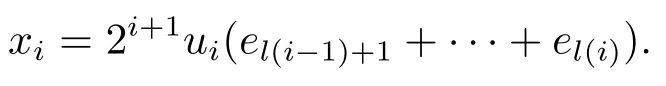
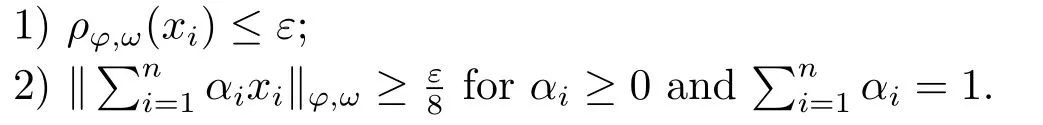
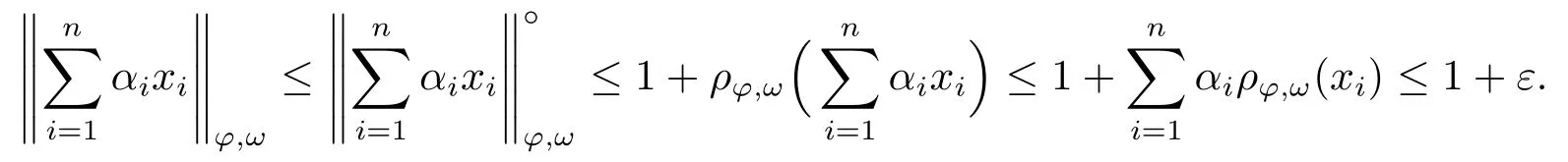
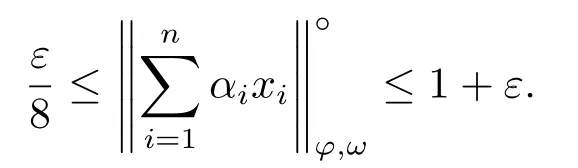
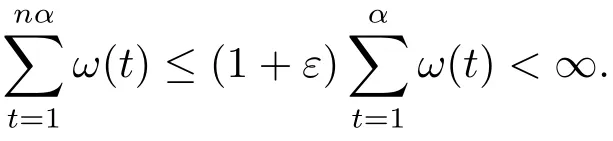
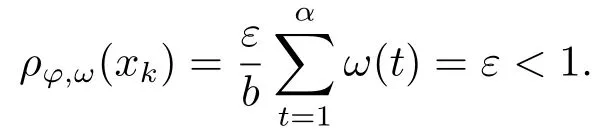

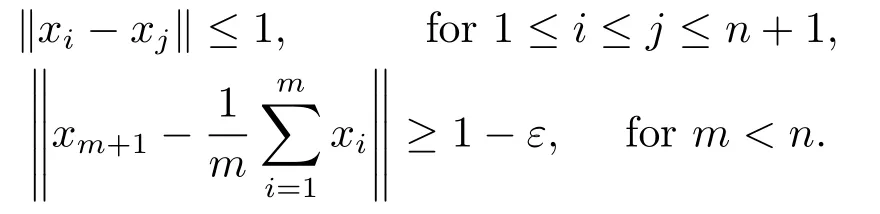
3.Uniformly Normal Structure of λ◦φ,ω
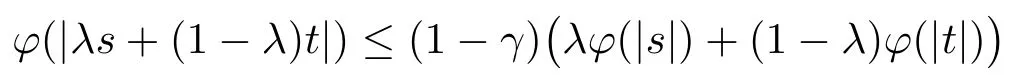
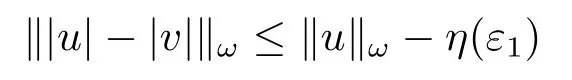
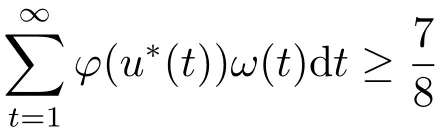
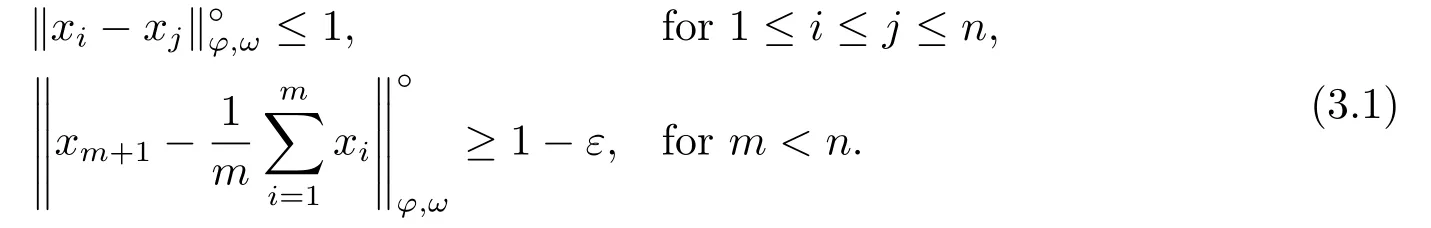
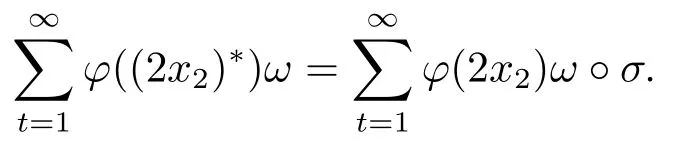
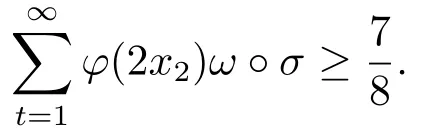
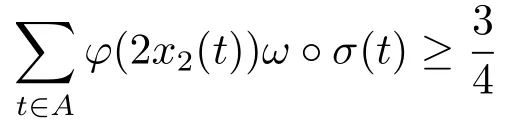
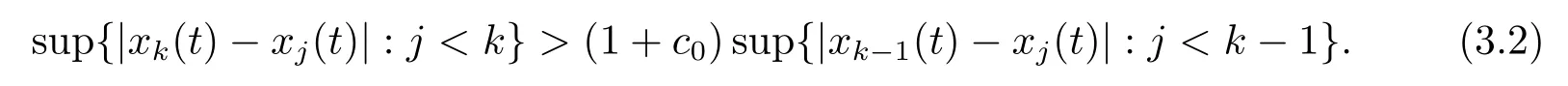

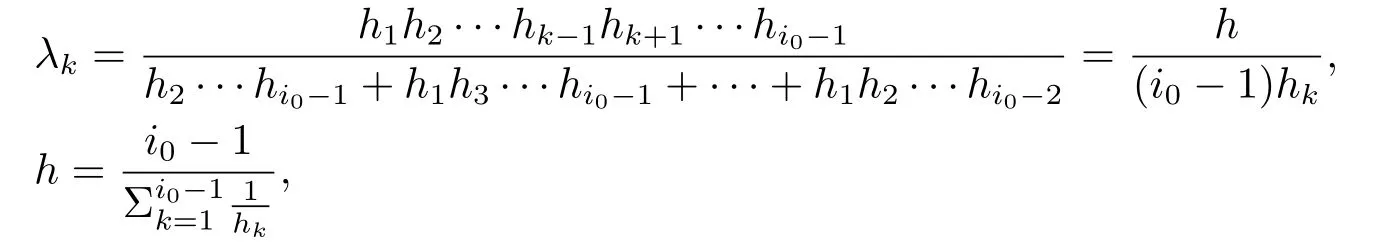
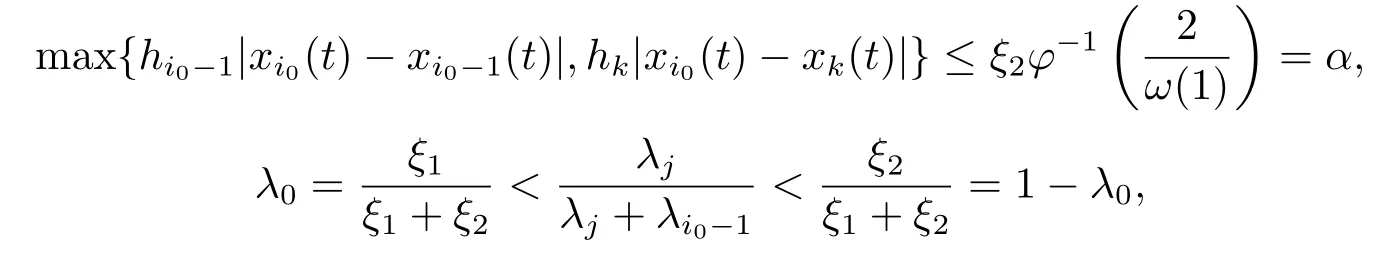


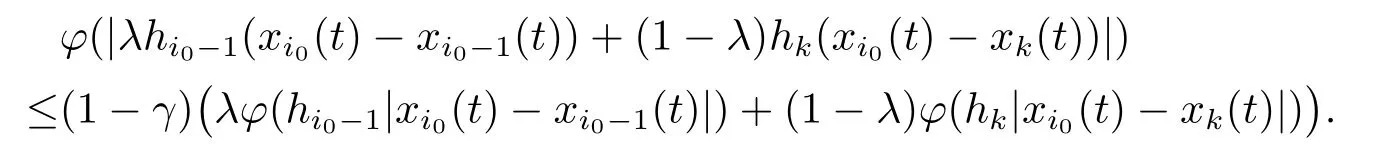
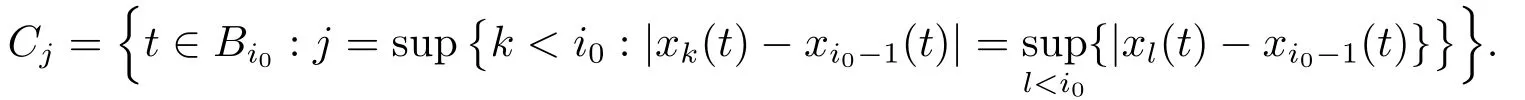
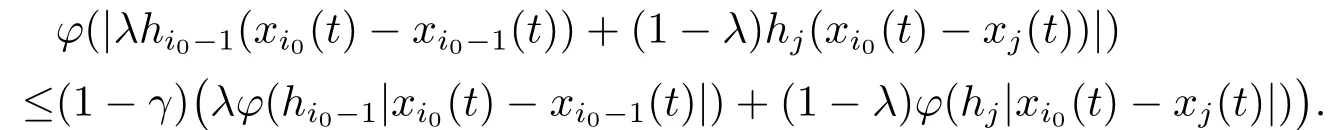
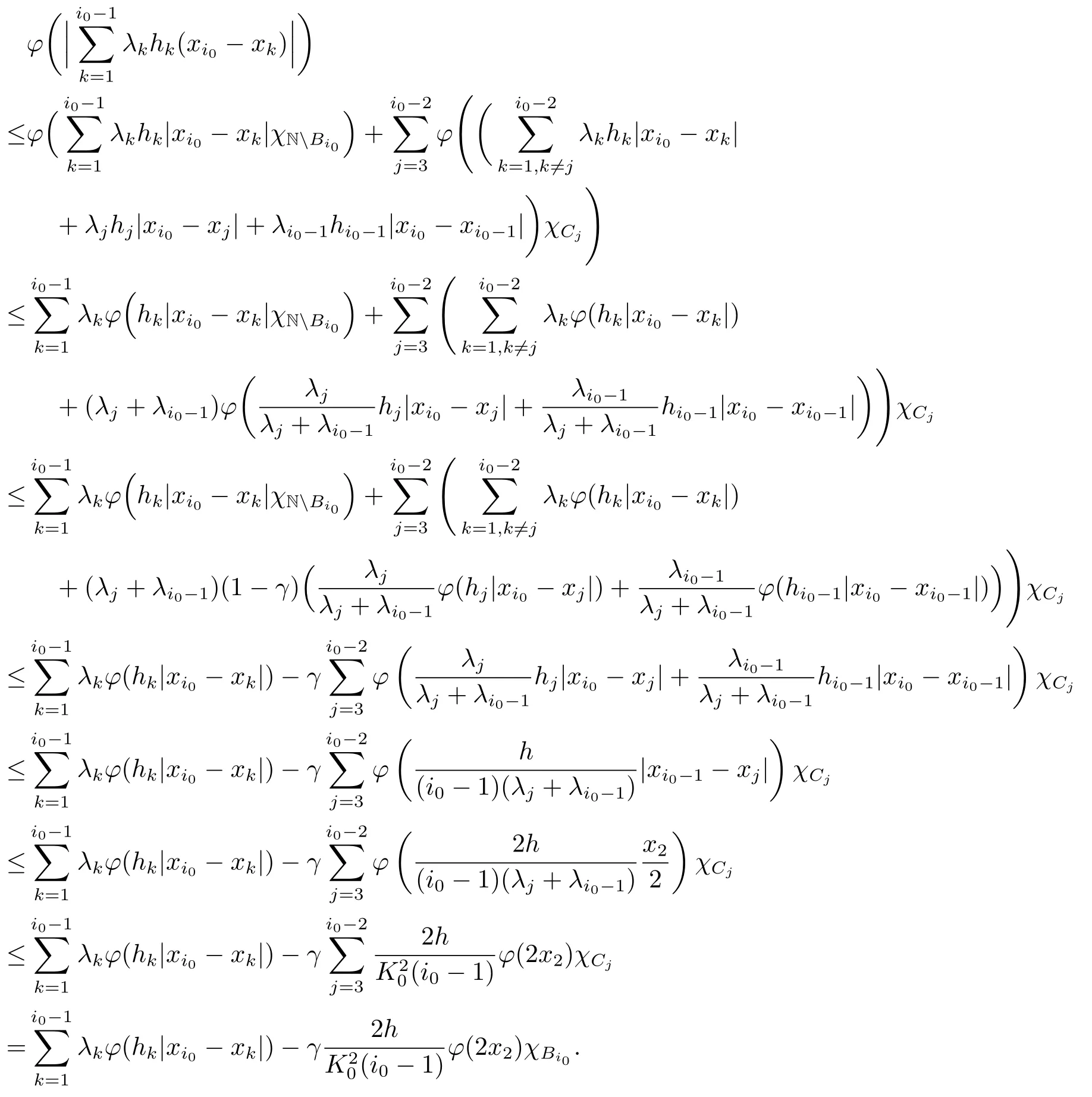
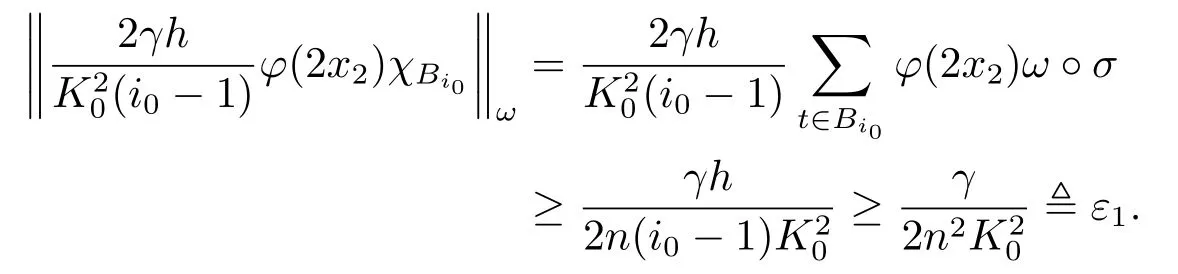
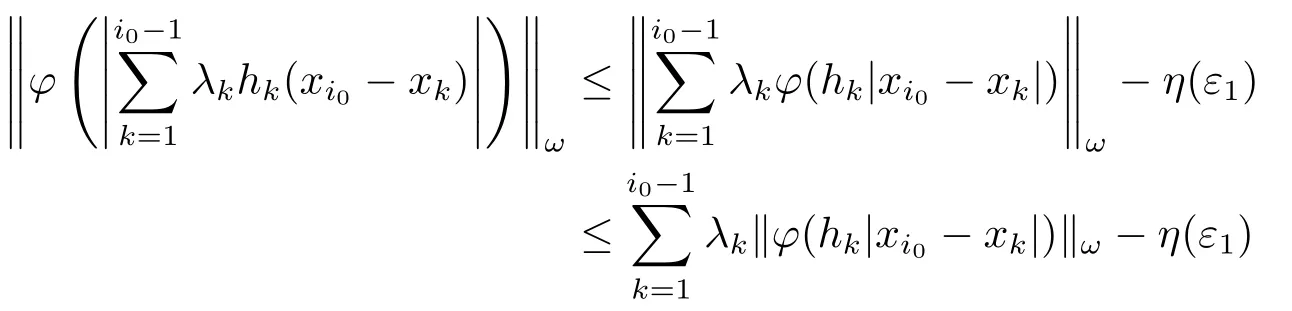
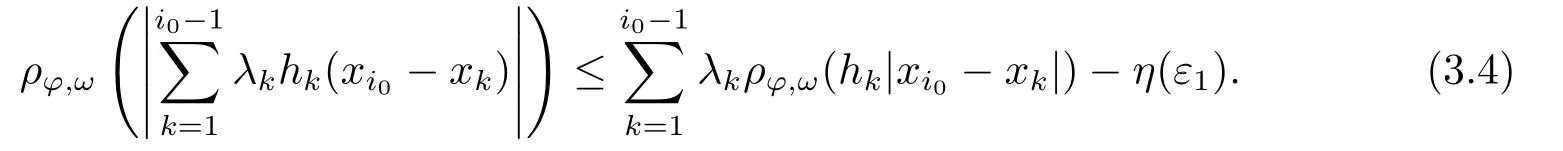
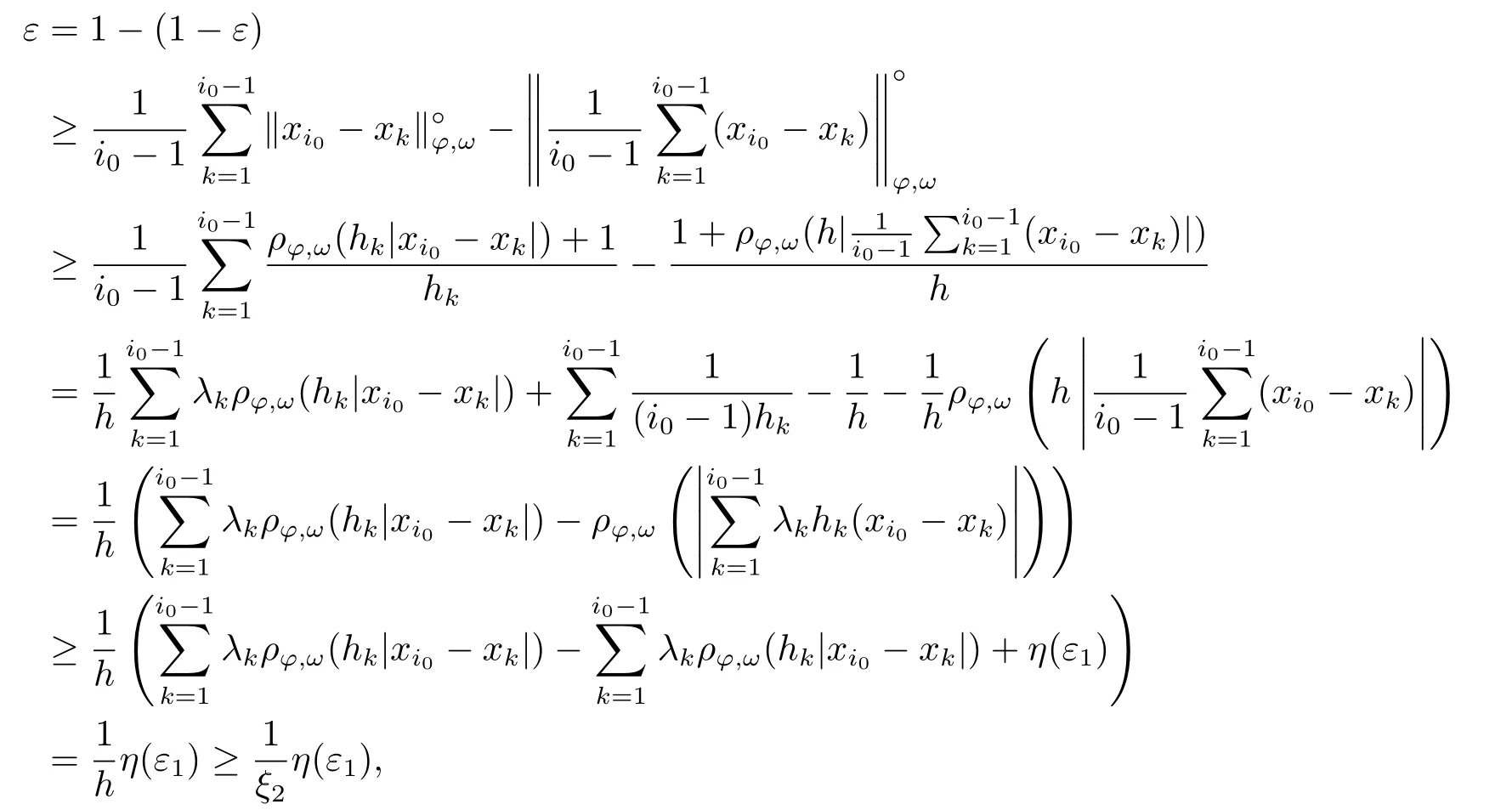
4.Uniform Non-Squareness Properties of λ◦φ,ω