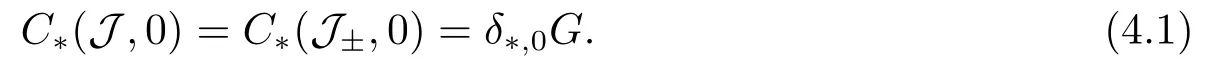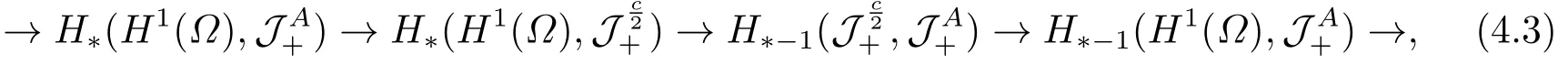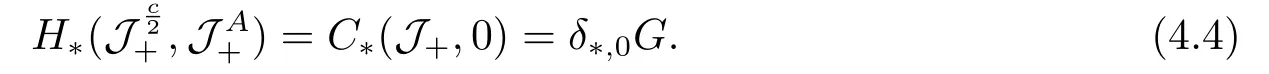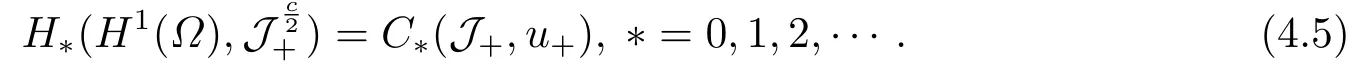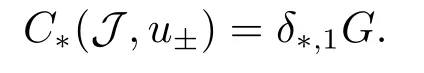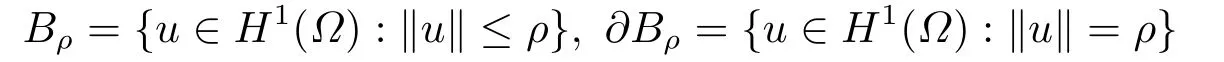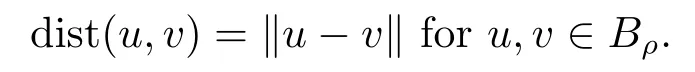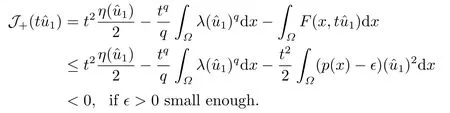Multiple Solutions for Robin Problem with Indefinite Potential and Concave Nonlinearities
XIA Hongming(夏鸿鸣),PEI Ruichang(裴瑞昌),ZHANG Jihui(张吉慧)
(1.School of Mathematics and Statistics,Tianshui Normal University,Tianshui 741001,China;2.School of Mathematics Sciences,Nanjing Normal University,Nanjing 210097,China)
Abstract: We investigate semilinear Robin problem with indefinite potential and right-hand-side nonlinearity which is exhibits-sublinear term of the form λ|u|q−2, 1 Key words: Robin problem;Morse theory;Indefinite potential;Concave nonlinearity;Existence and multiplicity of solution LetΩbe a bounded domain in RNhaving aC2-boundary∂Ω,In this paper,we consider the following semilinear Robin problem In this problem,ξ ∈Ls(Ω)(s >N)is an indefinite potential function,1 withn(·)being the outward unit normal on∂Ω.The boundary coefficientβ ∈W1,∞andβ(x)≥0 for allx ∈∂Ω.Let us briefly recall the variation formulation of the problem.The spaces which we will work in the study of problem (1.1)are the Sobolev spaceH1(Ω),the Banach spaceC1()and the “boundary” spacesLp(∂Ω)(1≤p ≤∞). LetH1(Ω)be the Hilbert space equipped with the inner product and the induced norm This cone has a nonempty interior which contains the set On∂Ωwe will use the (N −1)-dimension Hausdorff measureσ.Then,fromσ,we can define the boundary Lebesgue spacesLp(∂Ω)(1≤p ≤∞). By the theory of Sobolev spaces,we know that there exists a unique completely continuous linear operatorγ:H1(Ω)→L2(∂Ω)such that In order to simplify notation,we letuin place ofγ(u)when no confusion can happen.The symbol∥u∥qwithq ≥1 denotes the usual norm ofLq(Ω).Write 2∗for the critical exponent of the Sobolev embeddingH1(Ω)⊆Lq(Ω).Recall thatif 2 Also,we here only simply recall the knowledge about the spectrum of the indefinite potential operator−∆u+ξ(x)uwith Robin boundary condition.For detailed introduction,see [1].Let us consider the following linear eigenvalue problem: Suppose that (Ω)ifN ≥3,ξ ∈Lp(Ω)withp>1 ifN=2 andξ ∈L1(Ω)ifN=1; • β ∈W1,∞(∂Ω),β(x)≥0 for allx ∈∂Ω. Consider theC1-functionalη:H1(Ω)→R defined by From [1],we know that there existµ,c0>0 such that By (1.3)and the spectral theorem for compact self-adjoint operator on a Hilbert space,we obtain a strictly increasing sequence{}k≥1of distinct eigenvalues of problem (1.2)such that→+∞ask →+∞.Particularly,we obtain thatis a positive eigenfunction corresponding to the principal eigenvalue.Furthermore,from [2],we know that∈D+ifξ+∈L∞(Ω). In what followsA ∈L(H1(Ω),H1(Ω)∗)is the continuous linear operator defined by As usual,u ∈H1(Ω)is a weak solution of problem (1.1)provided with for allφ ∈H1(Ω). Also,we say that the Hilbert spaceH1(Ω)has the“Kadec-Klee property”,if the following implication holds: Now,we introduce the minimal hypothesis on thef(x,u)of problem (1.1): (H1)f:Ω ×R→R is a Carathéodory function withf(x,0)= 0 for a.e.x ∈Ωand satisfies the growth condition: for someC >0 andγ ∈(2,2∗),whereif 2 It is well known that the problem (1.1)is the analog of semilinear elliptic Dirichlet problems of the type where ∆u=div(∇u)is the usual Laplacian,1 Forλ<0,the existence of nontrivial solutions of(1.5)has been studied by many authors.For example,D’Paiva and Massa[3]used the Ambrosetti-Rabinowitz condition and assumed that and have proved that there existsλ∗<0 such that(1.5)has at least three nontrivial solutions forλ ∈(λ∗,0),where 0<λ∗1<λ∗2<···are the eigenvalues of−∆inW1,20(Ω).In the case thatf(x,u)is sublinear or asymptotically linear at infinity,we refer to [3-4] for details and further references. Forλ >0,Ambrosetti et al.[5]assumed that the nonlinearityfsatisfies the usual the Ambrosetti-Rabinowitz condition: (f1)There exist constantsθ >2 andM >0 such that and have obtained that the problem (1.5)has multiple nontrivial solutions.Whenf(x,u)is asymptotically linear at infinity,we also refer to [6]. Particular,forλ <0,SUN[7]obtained three nontrivial solutions of problem (1.5)where the nonlinearityf(x,u)satisfies standard subcritical growth condition,(f1)and the following condition: (f2)There existsµ∗<λ∗1such that Motivated by their work,the purpose of this paper is to study the existence of multiple nontrivial solutions of problem (1.1)where the nonlinearityf(x,u)is superlinear or asymptotically linear at infinity.We use the minimax methods based on the critical point theory,the Ekeland variational principle,the Morse theory and truncation techniques. Here,we impose some assumptions on the data of problem (1.1)as following: H(ξ)ξ ∈Ls(Ω)withs>Nandξ+∈L∞(Ω). H(β)β ∈W1,∞andβ(x)≥0 for allx ∈∂Ω. (H2)uniformly forx ∈Ω,wherep(x)≥0 andp ∈L∞(Ω)satisfiesp(x)≤for allx ∈Ωandp(x) (H3)f(x,t)is superlinear or asymptotically linear at infinity,i.e. uniformly for allx ∈Ω,wherel ∈(,+∞]. (H4)There existθ ≥1 andC∗>0 such thatθF(x,t)≥F(x,st)−C∗for (x,t)∈Ω×R ands ∈[0,1],whereF(x,t)=f(x,t)t −2F(x,t). Now,we present our main results: Theorem 1.1Assume that the conditions H(ξ),H(β)and (H1)-(H4)hold.Ifl=+∞,then the problem (1.1)has at least three nontrivial solutions for anyλ ≤0. Remark 1.1As far as the problem (1.5)is concerned,this similar result first appears in [7].Compared with the version of Ambrosetti- Rabinowitz condition (f1)used in [7],the conditions (H3)and (H4)are very general.More detailed information for the origin and changing of the generalized superlinear conditions (H2),(H3)will be seen in [8].In the case ofλ= 0 for the problem (1.1),under the conditions which is similar to ours,the authors in[9] obtained three nontrivial solutions by using the Morse theory,but the method in [9] can not be directly applied to the problem (1.1)sinceλ<0.However,using the method in [10],for anyλ ≤0,we can provide some information for the critical group of the mountain pass solutions and find the third nontrivial solution.Therefore,Theorem 1.1 improves the result given in [9]. Theorem 1.2Assume that the conditions H(ξ),H(β)and (H1)-(H3)hold.Ifl ∈for somek ≥2,then the problem (1.1)has at least three nontrivial solutions for anyλ ≤0. Remark 1.2It is obvious that we deal with the asymptotically linear case of problem(1.1)owing to the condition (H3)withIn fact,whenλ=0,the problem (1.1)with the resonance occuring has been studied in [11],but their method can not deal with the caseλ<0.So our result partially improves Theorem 11 in [11]. Theorem 1.3Assume that the conditions H(ξ),H(β)and (H1)-(H4)hold.Ifl=+∞,there exists someλ∗>0 such that for 0<λ<λ∗,the problem(1.1)has at least five nontrivial solutions. Remark 1.3From the condition (H3)andλ>0,one easily observes that the problem(1.1)is concave at zero and superlinear at infinity.Under similar conditions,this case has been considered by [12].We can prove our result by using the Ekeland variational principle combined mountain pass theorem and our method is slightly different that of [12]. Theorem 1.4Assume that conditions H(ξ),H(β)and(H1)-(H3)hold.Iffor somek ≥2,there exists someλ∗>0 such that for 0<λ <λ∗,the problem (1.1)has at least five nontrivial solutions. Remark 1.4From the condition(H3)withandλ>0,one easily observes that the problem (1.1)is concave at zero and asymptotically linear at infinity.This case is never considered by others as far as we know.We can prove our result using the Ekeland variational principle,the mountain pass theorem combined the Morse theory and so our result is completely new. The paper is organized as follows.In Section 2,we present some necessary preliminary knowledge about compactness,mountain pass theorem and Morse theory.In Section 3,we prove some lemmas in order to prove our main results.In Section 4,we give the proofs for our main results.In the sequel,the lettercnot having been explained will be used to denote various constant whose exact value is irrelevant. In this section,we give some preliminary results which will be used in the sequel.First,we recall some definitions for compactness condition and a version of mountain pass theorem. Definition 2.1Let (X,∥·∥X)be a real Banach space with its dual space (X∗,∥·∥X∗)andJ ∈C1(X,R).Forc ∈R,we say thatJsatisfies the (PS)ccondition if for any sequence{un}⊂Ewith there is a subsequence{unk}such that{unk}converges strongly inX.Also,we say thatJsatisfies the (C)ccondition if for any sequence{un}⊂Xwith there is subsequence{unk}such that{unk}converges strongly inX. We have the following version of the mountain pass theorem[13−14]: Proposition 2.1LetXbe a real Banach space and suppose thatJ ∈C1(X,R)satisfies the condition for someα<β,ρ>0 andu1∈Xwith∥u1∥>ρ.Letc ≥βbe characterized by whereΓ={γ ∈C([0,1],X),γ(0)=0,γ(1)=u1}is the set of continuous paths joining 0 andu1.Then,there exists a sequence{un}⊂Xsuch that Next,we recall some concepts and results of the Morse theory.For the details,we refer to [15].LetXbe a real Banach space andJ ∈C1(X,R).K={u ∈X|J′(u)= 0}is the critical set ofJ.Letu ∈Kbe an isolated critical point ofJwithJ(u)=c ∈R,andUbe an isolated neighbourhood ofu,i.e.K ∩U={u}.The group is called the∗-th critical group ofJatu,whereJc={u ∈X|J(u)≤c}. H∗(·,·)is the singular relative homology group ofJat infinity is defined by We denote Letα<βbe the regular values ofJand set IfK={u1,u2,...,uk},then there is a polynomialQ(t)with nonnegative integer as its coefficients such that Then the critical points ofJ±are exactly the weak solutions of (1.1). Lemma 3.1Assume that the conditions H(ξ),H(β),(H1)and (H2)hold.Thenu=0 is a local minimum ofJandJ±for anyλ ≤0. ProofFrom the conditions (H1)and (H2),for givenϵ >0,there existsA1>0 such that This implies that wherem>0.Then usingγ >2,there existsρ>0 small such thatJ(u)≥0 as∥u∥≤ρ.Sou=0 is a local minimum ofJ.The case ofJ±is similar. Lemma 3.2Under the conditions H(ξ),H(β),(H1),(H2),(H3)withl=+∞and(H4),the functionalsJandJ±satisfy the condition (C)cfor anyλ ≤0. ProofWe only give the proof ofJ+,the cases ofJandJ−are similar. Let{un}⊂H1(Ω)be a sequence such that In order to prove the lemma,we divide two steps to prove it. Step 1 We first prove that{un}is bounded inH1(Ω).Letu+n= max{un,0},u−n=min{un,0}.From (3.1),we get whereϵn →0 asn →∞,then the boundedness ofu−ncan be directly obtained.For the case ofu+n,by contradiction,we assume that∥u+n ∥→∞asn →∞.Letvn=∥u+n ∥−1u+n,then∥vn∥=1.By previous knowledge,up to a subsequence,we have Case 1 Suppose thatv0,then the Lebesgue measure ofΩ0={x ∈Ω:v(x)0}is positive.Using (3.1),we get which means that we can findM∗>0 such that By (H3),there is a constantM >0 such that then we have On the other hand,forx ∈Ω0,u+n →∞asn →∞.Then by the Fatou’s lemma and (H3)we imply that This combining with (3.7)gives that This is a contradiction with (3.6).Then this case is impossible. Case 2 Assume thatv=0.Let{tn}⊂R such that For anym>0,we assume that thenwn →0 inLq(Ω).So from the conditions (H1)and (H2),for everyϵ>0,we can find a constantC(ϵ)>0 such that which implies that which means that According toJ+(0)=0 andJ+(u+n)→c,we havetn ∈(0,1),then Then,from (H4)it follows the that This contradicts the fact thatJ+(tnu+n)→∞.Hence{un}is bounded,that is,there exists a positive constantM1such that Step 2 We prove{un}has a convergent subsequence.In fact,we can suppose that Now,sinceΩis a bounded domain,by the conditions (H1)and (H2),we can find a constantA2>0 such that then Similarly,sinceun ⇀uinH1(Ω),Subsequently,we can imply that By (3.12),we have Thus,we have which means thatJ+satisfies the condition (C)c. Lemma 3.3Assume thatλ ≤0,and the conditionsH(ξ),H(β),(H1),(H2),(H3)withl=+∞and (H4)hold.Ifu±are the isolated nontrivial critical points ofJ±,then we have ProofLet thenJssatisfies the condition (C)cby Lemma 3.2,andu+is a critical point ofJsfor alls ∈[0,1]. Now,we claim thatu+is the only critical point ofJsin a neighborhood ofu+for alls ∈[0,1]. Arguing by contradiction,we assume that there is a sequencesn ∈[0,1] and a critical pointun ∈H1(Ω)ofJsnsuch that Sinceu+>0 is the isolated critical point,we have Thus,fromunis the critical point ofJsn,we get This gives which implies that where 0<δ <1.This leads to a contradiction.Using the homotopy invariance of the critical groups (see [15]),we know that The case ofJ−is similar. Lemma 3.4Assume that the conditions H(ξ),H(β),(H1),(H3)withl=+∞and(H4)hold.Then we have ProofWe only give the proof ofJ+and the others are similar.LetS={u ∈H1(Ω):∥u∥=1,u+0}andB∞={u ∈H1(Ω):∥u∥≤1}.By (H3),for anyM2>0 there existsc>0,such thatF(x,t)≥M2t2−c,for (x,t)∈Ω×R,which implies for anyu ∈S.From (H4),we get Choose Then for anyu ∈S,there existst>1 such thatJ+(tu)≤a,that is which implies by (3.14) Therefore,by implicit function theorem,there exists a uniqueT ∈C(S,R)such that LetS1={u ∈H1(Ω)| ∥u∥≥1,u+0}.We construct a strong deformation retractτ:[0,1]×S1→S1which satisfiesifJ+(u)≥aandτ(s,u)=uifJ+(u) Lemma 3.5Under the conditionsH(ξ),H(β),(H2)and (H3)withthe functionalsJandJ±satisfy the standard condition (PS)for any fixedλ. ProofWe only give the proof ofJ,the cases ofJ+andJ−are similar.Let{un} ⊂H1(Ω)be a sequence such thatasn →∞.Since for allφ ∈H1(Ω).If∥un∥2is bounded,we can takeφ=un.From(H2)and(H3),there exists a constantc >0 such that|f(x,un(x))| ≤c|un(x)|,a.e.x ∈Ω.Sounis bounded inH1(Ω).If∥un∥2→+∞,asn →∞,setthen∥vn∥2= 1.Takingφ=vnin (3.15),it follows that∥vn∥is bounded.Without loss of generality,we assumevn ⇀vinH1(Ω),thenvn →vinL2(Ω).Hence,vn →va.e.inΩ.Dividing both sides of (3.15)by∥un∥2,we get Then for a.e.x ∈Ω,we haveasn →∞.In fact,ifv(x)0,from (H3),we can deduce that and Ifv(x)=0,we get Obviouslyv0,hence,lis an eigenvalue of problem (1.2).This contradicts our assumption. Lemma 3.6Under the conditions H(ξ),H(β),(H1),(H2),(H3)withl=+∞and(H4),the functionalsJandJ±satisfy the condition (C)cfor anyλ>0. ProofWe only sketchily give the proof ofJ+,the cases ofJandJ−are similar.This proof is essentially equal to our the previous section of the proof of Lemma 3.2 and the last section of the proof of Proposition 3 of [9].Hence,we omit it here. Theorem 3.7If the conditions H(ξ),H(β),(H1)and(H2)hold,then there existsλ∗>0 such that for all 0<λ <λ∗we can findρ >0 for which we havewhereBρ={x ∈H1(Ω):∥x∥<ρ}. ProofBy the conditions (H1)and (H2),givenϵ>0,there existsA3>0 such that for all (x,u)∈Ω×R.Then for allu ∈H1(Ω),we get wherec1,c2andc3are positive constants.By the basic computation,there existρ(ρ=andλ∗>0 such that for all∥u∥=ρand 0<λ<λ∗. In this section,we are ready to give the proofs of our main results. Proof of Theorem 1.1Since Lemma 3.2,we know thatJ,J±satisfy the condition(C)c.Also from Lemma 3.1 we know that 0 is a local minimum ofJandJ±.So,we have Using Proposition 2.1 and the maximum principle in [16],we getJ+(J−)has a critical pointu+>0(u−<0),andu±are also the nontrivial critical points of the functionalJ.Without loss of generality,we assume thatu±are isolated and the only nontrivial critical points of the functionalJ. Now we claim that Indeed,using the methods of[10],we letJ+(u+)=c>0.It follows from the homology exact sequence of the triplethat whereA<0 is a constant.Since 0 is the only critical point ofJ+in the setfrom (4.1),we get Similarly,sinceu+is the only critical point ofJ+in the setwe have Using Lemma 3.4,we get From (4.3)to (4.6),we obtain that The case foru−is similar. According to the claim and Lemma 3.3,we have The Morse equality (2.1)witht=−1 means that which leads to a contradiction.Thus,the problem(1.1)has at least three nontrivial solutions. Proof of Theorem 1.2From Lemma 3.1,Lemma 3.5 and the condition(H3)with Proof of Theorem 1.3Forρ>0 given by Lemma 3.7,define andBρis a complete metric space with the distance From Lemma 3.7,we get We claim that Indeed,fort>0 small enough,we have So,(4.9)is proved.By the Ekeland variational principle,we obtain a nonnegative critical pointu+1for the functionalJ+andJ+(u+1)<0 .Using the strong maximum principle,we getu+1>0.Hence,u+1is a positive weak solution of problem (1.1).Similarly,we also get a negative weaksolutionu−1fortheproblem(1.1). On theother hand,byLemma 3.7,Lemma3.6 and the condition (H3)withl= +∞,the functionalJ+has a mountain pass-type critical pointu+2andJ+(u+2)>0.Using the strongmaximumprinciple,we knowthatu+2>0.Hence,u+2is stilla positiveweaksolution of problem (1.1).Using thetruncated technique andthe mountain pass theorem,wecan also get a negative weak solutionu−2fortheproblem (1.1).Now,we canassume thatu+1andu−1are isolated local minima.Let us denotebthe mountain pass critical level ofJwith base pointsu+1,u−1: where By (H2)and slightly revising the proof of Theorem 5.1 of [19],we can know thatb <0 ifλis small enough.Since the condition (C)cholds because of Lemma 3.6,the level{J(u)=b}carries a critical pointu3ofJ,andu3is differentu±1.Thus,u+1,u−1,u+2,u−2andu3are five different nontrivial solutions of the problem (1.1). Proof of Theorem 1.4First,similar to the proof of Theorem 1.3,we haveu±1are two nonzero local minimums of the functionalJandC∗(J,u±1)=δ∗,0G. Second,by Lemma 3.7,Lemma 3.5 and the condition (H3)withthe functionalJ+has a mountain pass-type critical pointu+2andJ+(u+2)>0.Using the strong maximum principle and the regularity theory,we know thatu+2>0 andu+2∈D+.Hence,u+2is still a positive weak solution of problem (1.1)andC1(J+,u+2)0. Now,we can easily claim thatC1(J,u+2)=C1(J+,u+2)0.In fact,using the results in[16],we obtain Using the truncated technique and the mountain pass theorem,we can also find a negative solutionu−2for the problem (1.1)andC1(J,u−2)0. Finally,from the conditions(H1),(H2)and(H3)with,similar to the proof of Theorem 5.3 in[20],we haveC∗(J,0)=0,∗=0,1,2,··· .Using the condition(H3)and the result about critical groups at infinity in [18],we easily getC∗(J,∞)=δ∗,kG.Thus we find a weak solutionu3of problem (1.1)andC∗(J,u3)=δ∗,kG.Hence,by discriminating above critical groups,we know thatu+1,u−1,u+2,u−2andu3are five different nontrivial solutions of problem (1.1).1.Introduction





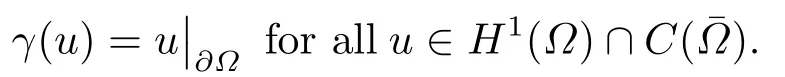







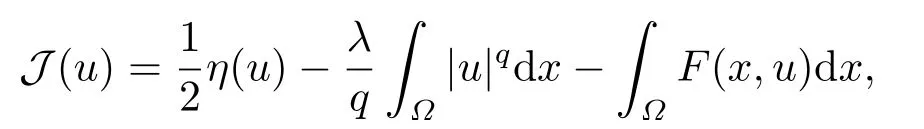



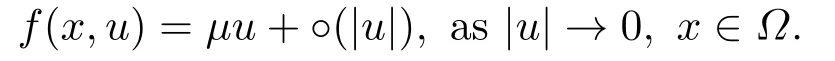
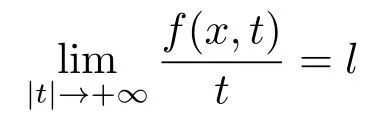
2.Preliminaries

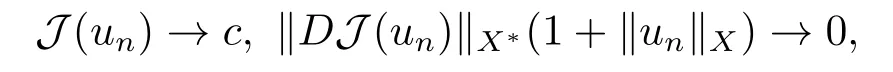
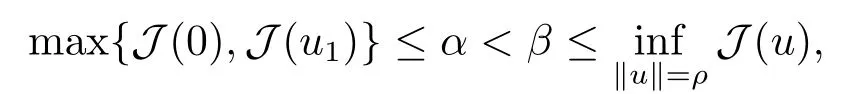

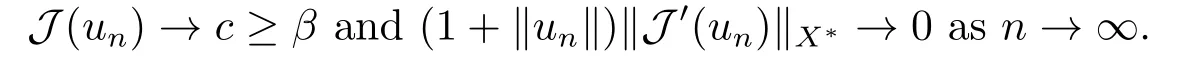
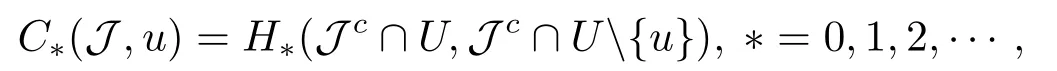

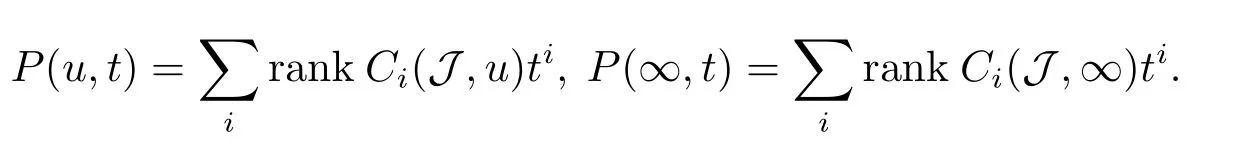
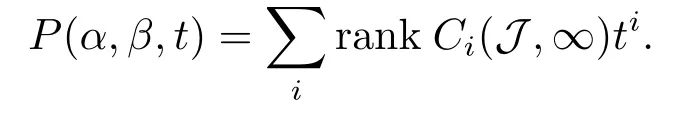

3.Some Lemmas




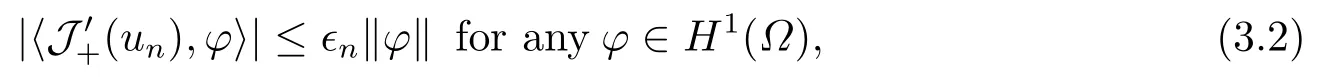

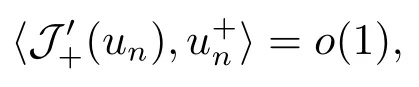


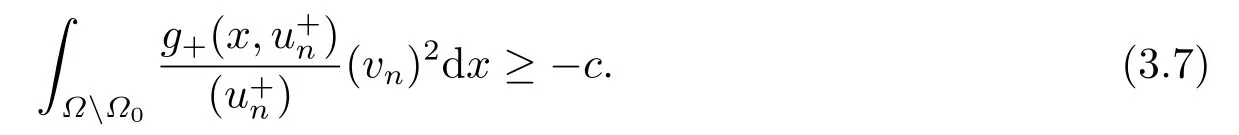

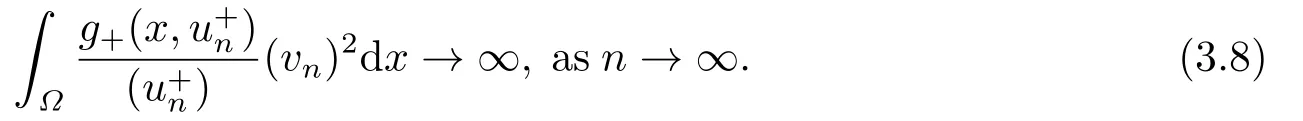
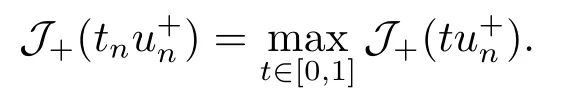





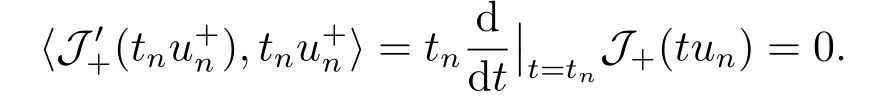

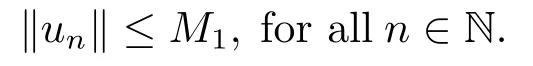


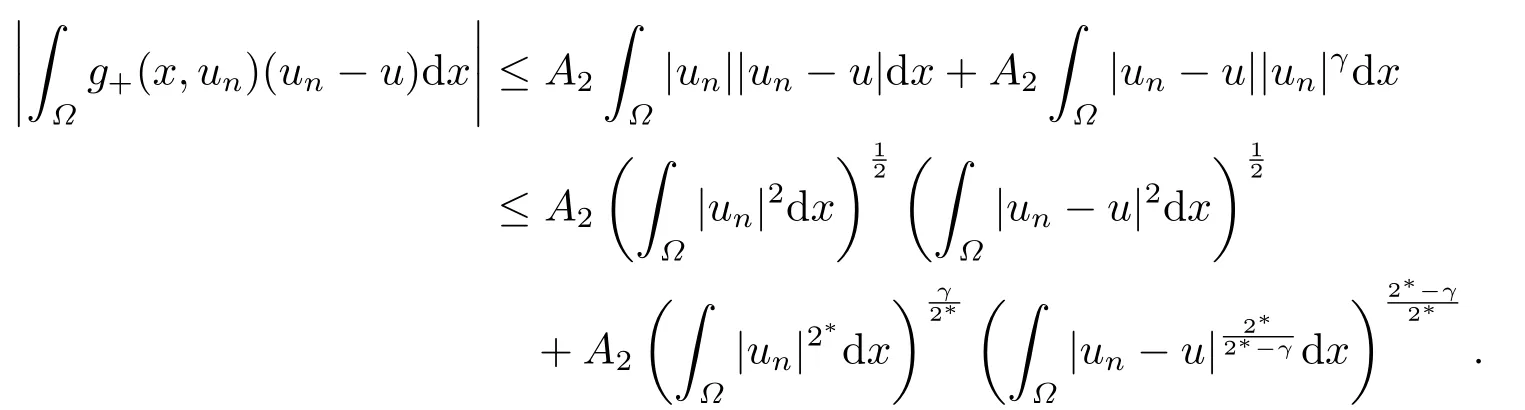
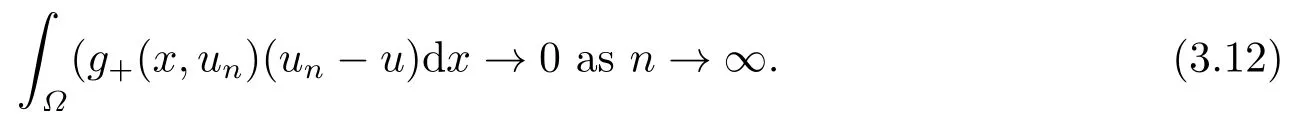
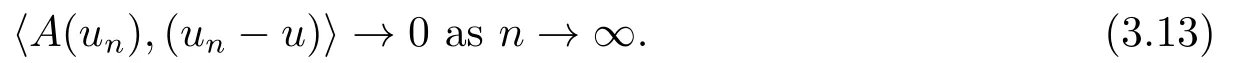
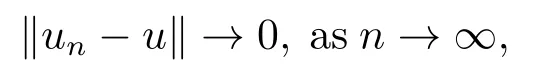

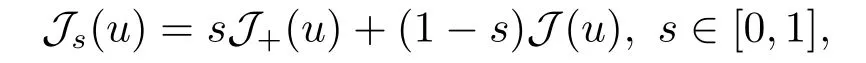
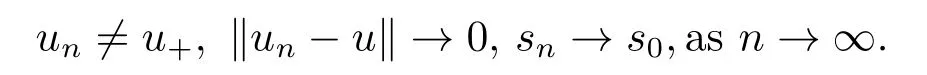

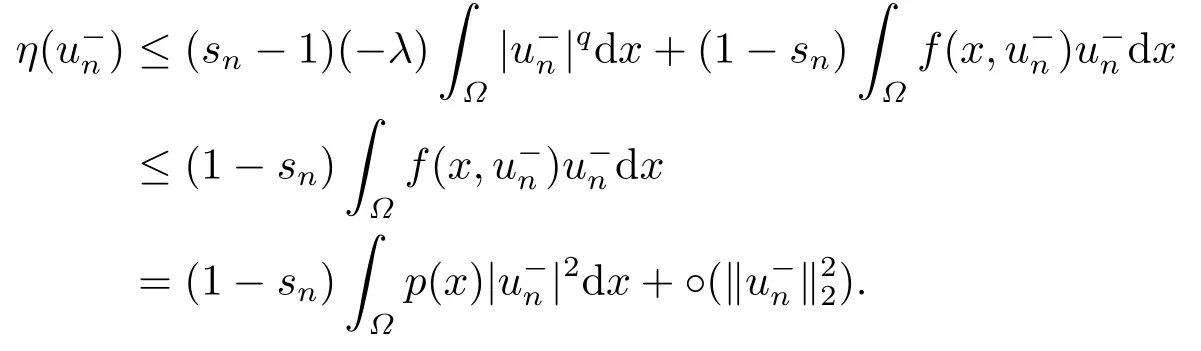

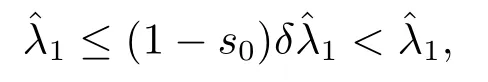

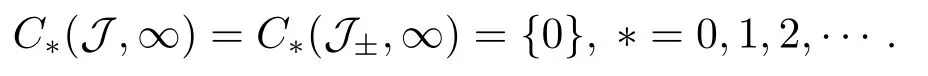

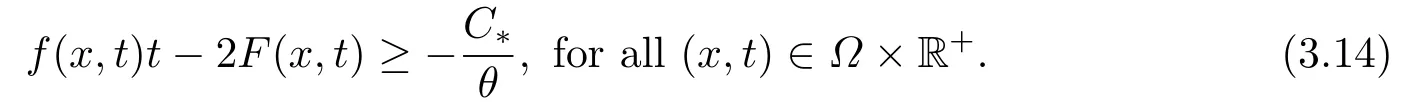

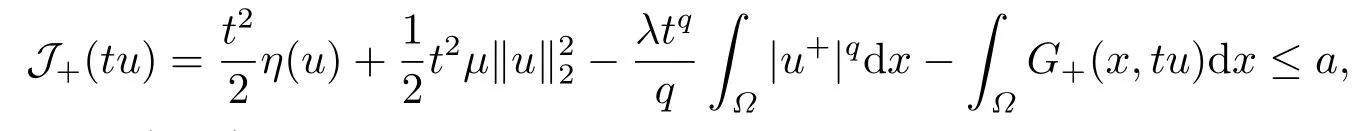

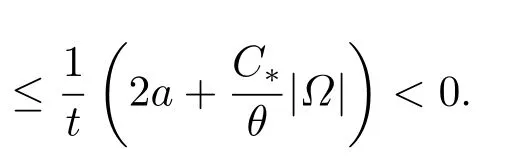


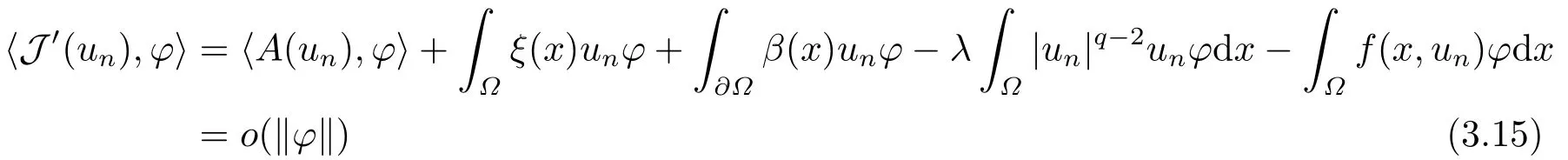
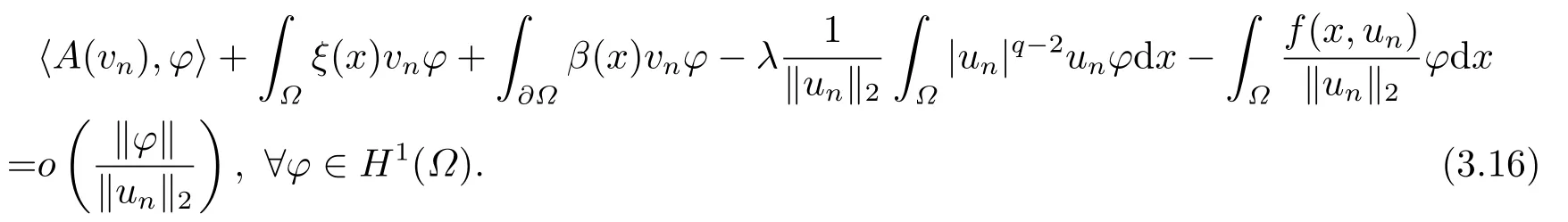
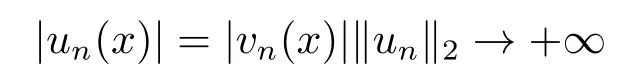
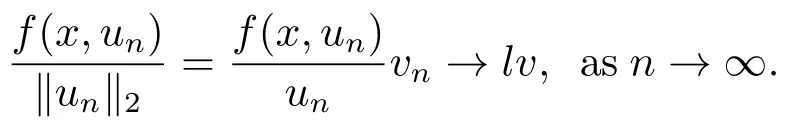





4.Proofs of the Main Results