Resource Allocation Based on User Pairing and Subcarrier Matching for Downlink Non-Orthogonal Multiple Access Networks

Zhixin Liu, Member, IEEE, Changjian Liang, Yazhou Yuan, Kit Yan Chan, and Xinping Guan, Fellow, IEEE

Abstract—The traditional orthogonal multiple access (OMA) is unable to satisfy the needs of large number of smart devices. To increase the transmission rate in the limited spectrum resource,implementation of both non-orthogonal multiple access (NOMA)and successive interference cancelation (SIC) is essential. In this paper, an optimal resource allocation algorithm in NOMA is proposed to maximize the total system rate in a multi-sector multi-subcarrier relay-assisted communication network. Since the original problem is a non-convex problem with mixed integer programming which is non-deterministic polynomial-time (NP)-hard, a three-step solution is proposed to solve the primal problem. Firstly, we determine the optimal power allocation of the outer users by using the approach of monotonic discrimination, and then the optimal user pairing is determined.Secondly, the successive convex approximation (SCA) method is introduced to transform the non-convex problem involving central users into convex one, and the Lagrangian dual method is used to determine the optimal solution. Finally, the standard Hungarian algorithm is utilized to determine the optimal subcarrier matching. The simulation results show that resource allocation algorithm is able to meet the user performance requirements with NOMA, and the total system rate is improved compared to the existing algorithms.

I. INTRODUCTION

WITH the rapid development and widespread use of smart devices, spectrum resources have become more and more scarce. Advanced mobile communication technologies are developed in order to satisfy the rapidly growing demands for mobile services and user experience requirements. Nonorthogonal multiple access (NOMA) has been recognized as a highly promising technology to satisfy the requirements of the fifth generation era on high spectral efficiency and massive connectivity [1].

In NOMA network, the co-channel interference is still caused since the effectiveness of the hardware is not satisfactory [2]-[4]. Several minimum aggregation level(MAL) algorithms with low complexity were developed based on mathematical analysis and simulation [5]. Despite low algorithmic complexity, the algorithms were able to generate much more multi-user diversity gain. Bourouha and Abdel-Qader [6] proposed a new cross layer design of dynamic resource allocation control for 3GPP2 1xEV-DV system. The proposed approach was able to achieve the optimal combination of system parameters and determine the overall throughput gain based on the requested service types.However, co-channel interference occurs and user quality of service (QoS) is diminished since the same frequency band is used by different users when using this type of allocation scheme [2], [4], [7]. Since the orthogonal frequency division multiple access (OFDMA) technology divides the entire frequency band into multiple sub-bands and only one user occupies one sub-band, no co-channel interference is caused between users. Therefore, the QoS of users can be significantly improved [8]-[11]. In [8], the author created a downlink OFDMA cognitive wireless network that maximized system energy efficiency through joint relay selection, channel allocation and power control. In [9], the author studied the power control and resource allocation problem in downlink OFDM networks, where co-channel interference exists among cells. Three optimization objectives, sum power minimization,sum rate maximization, and sum energy efficiency maximization, were jointly considered. For each sub-problem,the author developed a correspondingly distributed power control and resource allocation algorithm with low complexity. Li et al. [12] and Hao et al. [13] studied the approaches of joint resource allocation for OFDM-based cognitive radio networks with imperfect spectrum sensing.Although the total system rate obtained by the OFDMA is greatly improved, the achievable rate cannot satisfy the user requirements with the rapid development of Internet of things and artificial intelligence. Since one user fully occupies one sub-band, the utilization of spectrum resources is inefficient.

In order to use the limited spectrum resources more effectively, NOMA is combined with successive interference cancelation (SIC) technology, which is promoting in 5G network, enables multiple users; the combined approach attempts to share one frequency band resource, eliminate most interference, and increase the total transmission rate of system. The prospects and challenges of NOMA in 5G have been discussed in [14]-[16]. The spectral efficiency is improved with the emergent NOMA and SIC technologies[17]-[19]. Wu et al. [17] proposed an approach which attempted to improve the effectiveness of NOMA downlink relay-transmission, the power allocation strategy was developed for the base station (BS) and relays in order to maximize the overall throughput delivered to mobile users(MU). In [18], a two-slot secondary non-orthogonal multiple access (NOMA) relay was used to assist spectrum sharing,where the primary transceivers with long distance were connected through the relay. Sun et al. [19] have developed a resource allocation algorithm which was incorporated with the cooperative cognitive relaying multicarrier non-orthogonal multiple access (MC-NOMA) systems. The resource allocation approach attempted to maximize the weighted system throughput by jointly optimizing the power and subcarrier allocation for both the primary and the secondary networks; the approach also ensured that the QoS requirements of the primary users were satisfied. Considering the practical environment, Ding et al. [20] stated that typical NOMA scenarios were only involved with two users.However, the decoding complexity of the receiver increases significantly when more users occupy the same frequency band [21]. Orthogonal transmission was adopted between different cells or clusters, in order to avoid interference between different cells and reduce the decoding complexity at receiver [22]. In the 5G era, the relay application is essential to satisfy increasing demands of user accesses. The relay not only expands the coverage, but also plays a key role in resource scheduling [23], [24]. Zhang et al. [23] proposed two efficient many-to-many two-sided source-destination (SD)pair-subchannel matching algorithms, which can provide a sub-optimal solution to the resource allocation problem in affordable time. However, due to that one SD pair uses single subcarrier to communicate, the waste of spectrum resources is inevitable. The water filling algorithm is used for power control, which also causes unfair user power allocation.Chong et al. [24] proposed an alternating optimization-based algorithm. By analyzing the two situations of given power and given relay beamforming, the global optimal solution is finally found. However, with the assumption that all users share one channel to communicate, the high decoding complexity at the receiving end of the system limits the realization. Although the literature [17], [25], [26] all used relays to assist in maximizing the NOMA network rate, they omitted the problem of system decoding complexity. When the number of users increases, the communication system may break down. Our proposed optimal resource allocation strategy considers both the overall system rate and the decoding complexity of the system.

In this paper, we attempt to solve the joint resource allocation problem which is formulated to optimize power allocation, user pairing and subcarrier matching for downlink non-orthogonal multiple access networks. Each node in the network is installed with a single antenna, the central users are able to directly communicate with the base station and outer users communicate with aid of decode-and-forward (DF) relay nodes. The contributions of this paper are summarized as follows:

1) A joint resource allocation framework is proposed for relay-assisted two-layer multi-sector communication network,which combines OFDMA and NOMA to increase the overall sector rate and reduce the decoding complexity of the system.The allocation scheme consists of user pairing strategy, power allocation and subcarrier matching. The developed scheme is able to improve the achieved transmitting rate greatly.

2) To reduce decoding complexity caused by SIC between multiple users, the user pairing strategy is proposed. Different from the existing user pairing strategies, this paper uses a combination of monotonicity analysis and user pairing rate comparison to obtain the best user pairing strategy. This strategy is easy to calculate and can be extended to multiple users situations.

3) An optimization approach is proposed to solve the original resource allocation optimization problem which is a non-convex fractional mixed binary integer programming problem. The successive convex approximation (SCA)method is adopted to convert the original problem into a convex one. The Lagrangian multiplier method and the standard Hungarian method are developed to get the optimal solutions. Compared to the existing algorithms, the proposed algorithm can improve the total transmission rate while the algorithmic complexity is lower.

The rest of this paper is organized as follows. Section II presents the system model. In Section III, the optimization problem of total rate maximization is formulated including subcarrier matching, user pairing and power control.Simulation results and analysis are presented in Section IV.The conclusion is drawn in Section V.

II. SYSTEM MODEL

We consider an NOMA downlink cellular system as shown in Fig.1. In this cellular network, a single base station (BS) is at the center of the cell, and the cell is divided into S sectors.Each sector consists of I central users, a fixed relay, and J outer users. The downlink communication is considered, and the subcarriers are allocated to the different sectors and each sector occupies only one subcarrier for communication. The relay is responsible for forwarding information between the base station and outer users in corresponding sector. The relay node is operated in a half-duplex mode using the decode-andforward (DF) scheme. The channel on any subcarrier is assumed to be Rayleigh fading.

G. Algorithm Complexity Analysis

In the subcarrier allocation algorithm, n represents the dimension of the subcarrier matching matrix. We can determine the optimal total system rate when the number of iterations is TmaxZmaxin the worst case. The worst-cas e time complexity of the proposed algorithm is O(TmaxZmaxn3) and the complexity of the exhaustive method is O(TmaxZmaxn!).When n is large, the complexity of the Hungarian algorithm is lower than that of the exhaustive method. The complexity of the fixed subcarrier allocation (FSA) method is O(TmaxZmax),and the complexity of the channel state ordering (CSO)method is O(TmaxZmaxn). Although the complexity of two methods is low, the system performance obtained by the two methods is not satisfactory.

IV. SIMULATION RESULTS AND PERFORMANCE ANALYSIS

In this section, simulations analysis is given to evaluate the system performance. We consider a scenario with multisectors and multi-subcarriers which is engaged with a relay NOMA downlink communication network. The system consists of a base station, five sectors, five subcarriers and each sector contains a relay, two central users and four outer users. The base station is located at (0, 0); the distance from the BS to the central user and relay of different sectors are (40, 53), (35,42), (33, 45), (42, 55), (30, 50), respectively. The distance from relay in different sectors to their edge users are (55, 62.2,68.1, 70), (60, 57, 53.2, 55), (56.6, 52.2, 60, 50), (58, 55, 60.2,65) and (60, 65, 54.1, 70), respectively. The system parameters are given in Table I.

TABLE I SIMULATION PARAMETERS

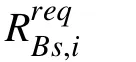
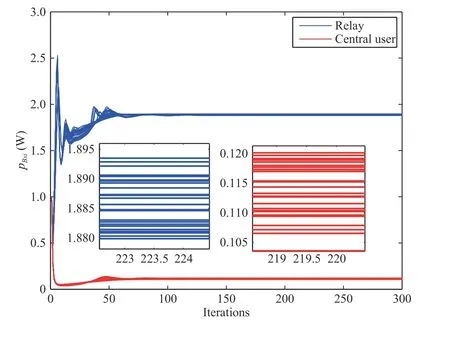
Fig.2. The convergence of the optimal subcarrier power.

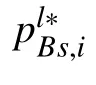
Fig.3 shows the total rates of the central user and those of the relays on the five subcarriers in the s-th sector. Fig.4 shows the rate of the outer user on the five subcarriers in the s-th sector. Since we have sorted the channel gains of the users, the rate is still lower than that of users with good channel gain, although more power is assigned to the users with poor channel gain.

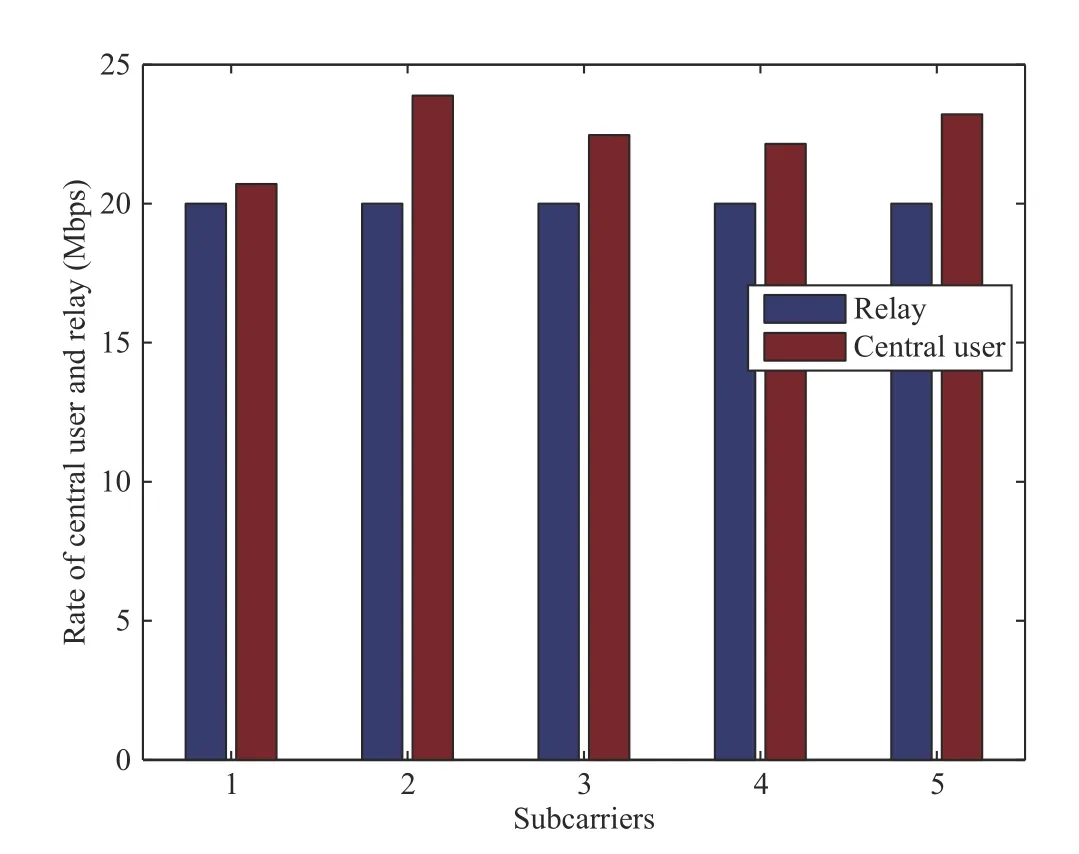
Fig.3. The optimal power of the central user and relay in the s-th sector.

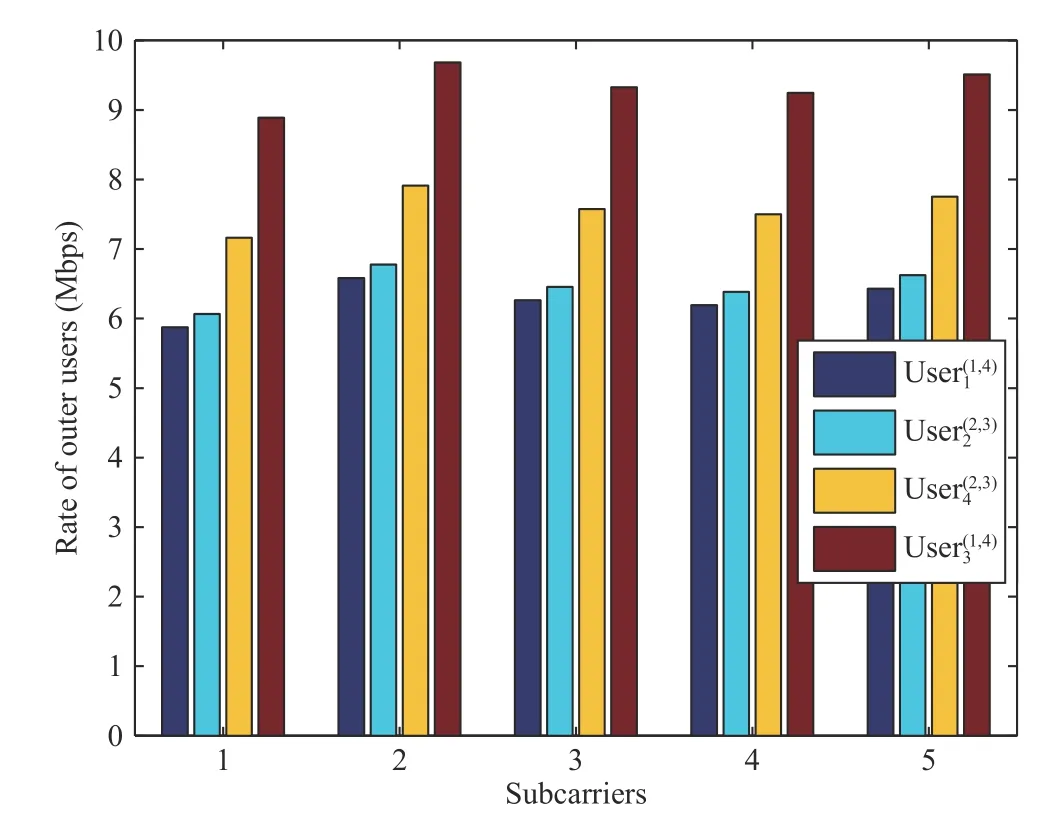
Fig.4. The optimal power of the outer users in the s-th sector.

Fig.5 shows the total system rate for the three cases when different Psmaxare considered. The theoretical analysis in Section III-B shows that Rcase1＜Rcase2＜Rcase3. Fig.5 verifies the theoretical analysis. In order to maximize the total system rate, users are not necessary to be paired in this process when combining NOMA and SIC. However, the complexity of the receiving system is greatly increased when the number of users is increased. In order to balance the total system rate and receiver complexity, user pairing is used.

Fig.5. Total system rate for three user pairing cases with four users.

Since the proposed algorithm attempts to maximize the total rate of the system, the performance of the proposed algorithm is verified by comparing to several different power control algorithms. Figs. 6 and 7 show the total rates when different transmit power thresholds of the BS and the relay are used.The compared algorithms are traditional OMA [9], equal subcarrier power allocation (ESPA) and proportional power allocation (PPA) algorithms [28]. The total system rate obtained by the proposed power control algorithm is generally higher than those of the other tested algorithms, since the user pairing and NOMA combined with SIC are integrated. It is noted that although the ESPA and PPA algorithms achieve lower total system rates, they are with simpler power allocation mechanisms.

Fig.6. The comparisons of total system rates with different P Bsmax.

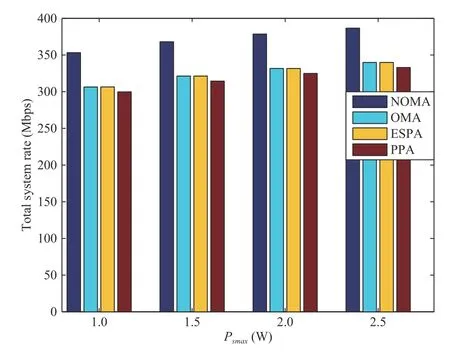
Fig.7. The comparisons of total system rates with different Psmax.

Fig.8 shows the total system rate of central users and relay in each sector versus different minimum rate thresholds. It is essential for users with poor channel conditions to satisfy their performance requirements; the remaining resources are allocated to users with good channel conditions to maximize the total system rate. Note that because the minimum rate threshold Rreqof each cell is the same, the rate of relay for each cell is also the same. Therefore, we only draw one curve of the relay in Fig.8. As the minimum rate threshold increases, the user with good channel gain (central user) needs to allocate some of its own resources to the relay, in order to satisfy the minimum rate requirement of the users with poor channel gain (relay). As a result, the rate of the central user decreases and the rate of the relay increases. When a large amount of information is required to be transmitted by the relay, the minimum rate threshold can be increased to satisfy the requirement.

Fig.8. The rates of central users and relay with different R req.

Fig.9 shows the comparison of total system rate when different subcarrier selection methods are used. The performance of our proposed optimal NOMA subcarrier matching algorithm is the same as the exhaustive method.However, the complexity of the proposed optimal NOMA subcarrier matching algorithm is O(TmaxZmaxn3), the complexity of the exhaustive method is O(TmaxZmaxn!).Besides, the complexity of fixed subcarrier allocation (FSA) is O(TmaxZmax) and the complexity of Channel status ordering(CSO) algorithm is O(TmaxZmaxn) [29]. It is found the total system rates of the FSA and CSO are lower than those of the optimal NOMA subcarrier matching algorithm.

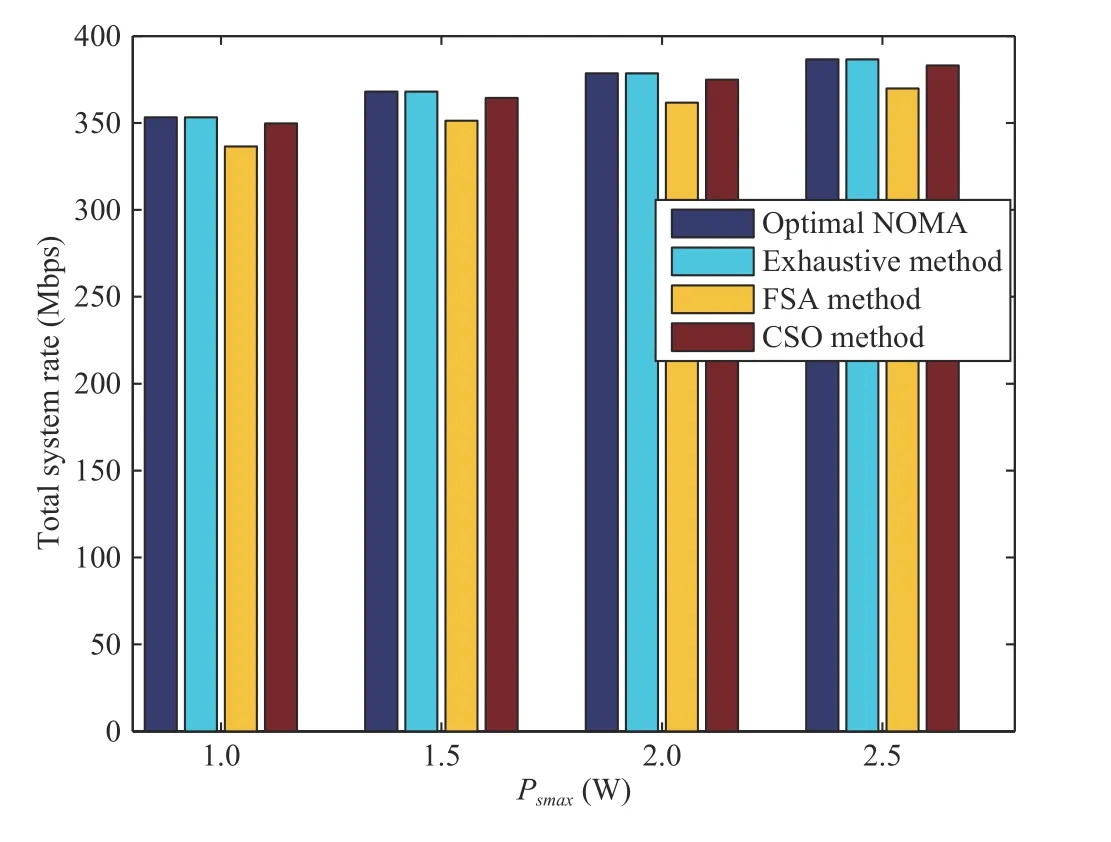
Fig.9. Comparisons of total system rate with different selection strategies.

V. CONCLUSIONS

In this paper, an optimal power control algorithm is proposed to maximize the total system rate in a multi-sector multi-subcarrier relay-assisted communication network; also the optimal joint subcarrier matching and user pairing algorithms in NOMA are presented. In the proposed scheme,the optimal power allocation of the outer users can be determined by the monotonic discrimination, and then the optimal user pairing can be obtained by analyzing the user pairing situation of four users. The successive convex approximation method is used to transform the non-convex problem involving the central users into a convex one. The Lagrangian dual decomposition is used to determine the optimal power allocation. Finally, the standard Hungarian algorithm is adopted to determine the optimal subcarrier matching. The simulation results and algorithm complexity analysis show that our algorithm is able to achieve higher total system rate with lower algorithmic complexity.