Resilience Against Replay Attacks: A Distributed Model Predictive Control Scheme for Networked Multi-Agent Systems
Giuseppe Franzè, Senior Member, IEEE, Francesco Tedesco, Member, IEEE, and Domenico Famularo
Abstract—In this paper, a resilient distributed control scheme against replay attacks for multi-agent networked systems subject to input and state constraints is proposed. The methodological starting point relies on a smart use of predictive arguments with a twofold aim: 1) Promptly detect malicious agent behaviors affecting normal system operations; 2) Apply specific control actions, based on predictive ideas, for mitigating as much as possible undesirable domino effects resulting from adversary operations. Specifically, the multi-agent system is topologically described by a leader-follower digraph characterized by a unique leader and set-theoretic receding horizon control ideas are exploited to develop a distributed algorithm capable to instantaneously recognize the attacked agent. Finally, numerical simulations are carried out to show benefits and effectiveness of the proposed approach.
I. INTRODUCTION
SEVERAL infrastructure systems are of major and crucial importance to society, as they significantly affect our daily life: power grids, telecommunication systems, water supply,and so on. In the last decade, ongoing integration of information technologies into such facilities [1], [2], has gained an increasing relevance within the control community.
On one hand, these advances have boosted the emergence of networked control systems (NCSs) where information networks are tightly coupled to physical processes and human intervention, see [3] and references therein. Going into more detail, these systems are operated by means of computers and applications using communication networks to transmit information through wide and local area networks:measurements are transmitted to the control centers; control data are forwarded to the system’s actuators; information is exchanged between control centers [4].
On the other hand, NCSs lead to several challenges when cyber and physical components are combined into a uniform infrastructure: amongst them security is by no means the most important issue [5]. Open and public communication channels, susceptible to even minor disturbance in the environment, may indeed ease physical system impairments or damages by malicious agents at worst. Adequate protection actions and/or countermeasures are then required by designing ad-hoc schemes capable to provide security mechanisms both for cyber and physical layers, see [6], [7]. Moreover, modern systems have an increasingly complex structure due to large number of interacting agents aligned to accomplish specific tasks in a distributed fashion. Multi-agent architecture features make the security issue more challenging because the subsystem vulnerability can lead to fragility of neighbor subsystems, see [8], [9], and references therein.
On this issue, NCS research efforts are directed to analyze two main topics: attack detection and attack-resilient control.As the attack detection is concerned, false data injection attacks against state estimation have been studied in [1], [10],[11]. On the other hand, contributions pertaining to multiagent systems can be found in [12] and [13], where conditions under which misbehaving agents can be detected have been developed. Replay attacks, which iterating in malicious fashion transmitted data, have been analyzed in [14]. By referring to the attack-resilient control, the main aim was to derive admissible/efficient strategies for mitigating the undesired effects on the control loop signals. In spite of its relevance, few contributions have addressed such an issue. In particular, denial-of-service (DoS) attacks, which are capable to destroy the data availability in control systems, have been tackled in [15]-[17]. In [18], a distributed receding-horizon control law has been proposed to ensure that vehicles reach the desired formation despite DoS and replay attack occurrences. Moreover, a recent contribution [19] has a twofold interest: 1) It is proved that a stealthy attack on a single agent does not reflect along the network as a difference with the other agent states; 2) A distributed H∞control protocol is designed to soften the attack effect by solving nonhomogeneous game algebraic Riccati equations.
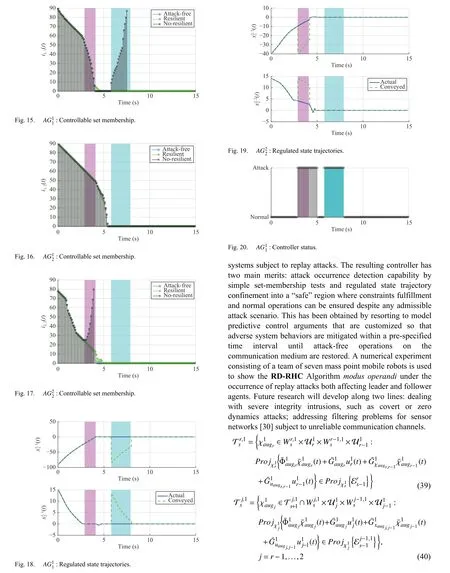
Moving from this analysis, we propose here a distributed control strategy based on the receding horizon philosophy [20]that can be more adequate to deal with attack-resilient scenarios [21]. In fact a receding horizon control scheme has been proved to be extremely useful to manage simultaneous management of direct constraints fulfillment, disturbance/noise rejection and unpredictable attack occurrences [22],[23]. Going into details, the main aim is at developing a discrete-time receding horizon control (RHC) strategy for constrained regulation problems in networked multi-agent systems subject to replay attacks on the communication medium. This is one of the first attempts on this topic to develop an efficient resilient control strategy when severe cyber attacks affect the normal operation in constrained multiagent systems.
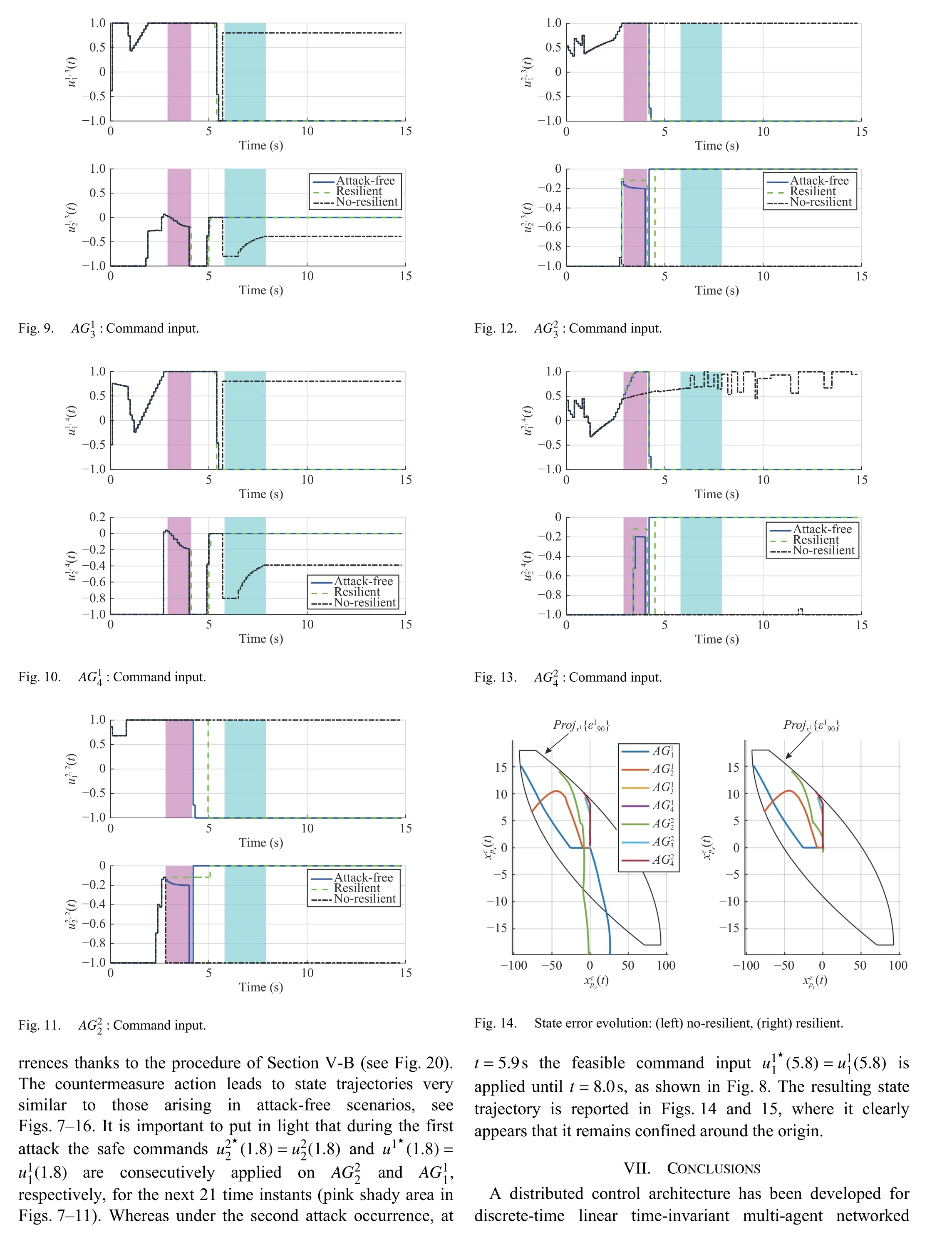
In particular, the key attribute of the resulting scheme is to provide guaranteed countermeasures to unpredictable phenomena via a formal reconfiguration control law. By taking advantage of the set-theoretic approach first proposed in [24] and extended to the leader-follower (LF) framework in[25], the controller is capable to take care of (possibly)unknown information on the attack occurrence. To this end,the RHC unit is designed so that the multi-agent system behavior is encapsulated in a pre-computed state space region until safe communications are re-established.
The main paper contribution can then be summarized as developing an efficient resilient control strategy when severe cyber attacks affect the normal operation in constrained multiagent systems. Noticing that the attack is unpredictable and the detection must be performed on the controller side make the problem extremely difficult to be tackled on. As a consequence, it is required that on the plant side a viable command is always available.
The paper is organized as follows. In Section II, the problem to solve is formally stated. Section III summarizes literature results to be exploited in the subsequent developments. In Section IV, a set-theoretic customization to the multi-agent framework is provided, while in Section V the proposed resilient strategy is detailed. Finally, simulations and some remarks end the paper.
Notations:
Consider the following discrete-time linear time-invariant(LTI) system:
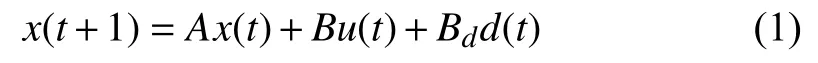
where x(t)∈Rndenotes the state, u(t)∈U ⊂Rmthe constrained input and d(t)∈Rwthe process disturbance. It is assumed that d(t)∈D ⊂Rd, ∀t ∈Z+:={0,1,...}, with D a compact set and 0d∈D.
Definition 1: A set T ⊆Rnis robustly positively invariant(RPI) for (1) if once the state x(t) enters the set at any given time t0, all future states remain confined within regardless any disturbance realization affecting the plant, i.e., x(t0)∈T ⇒∃u(t)∈U s.t.x(t+1)∈T,∀d(t)∈D, ∀t ≥t0.
Definition 2: Given the plant (1) it is possible to compute the sets of states i-step controllable to T0:=T via the following recursions (see [26]):
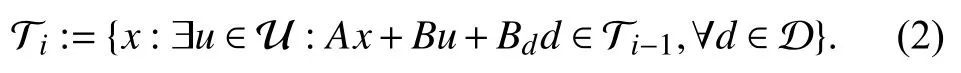
Definition 3: Given the plant (1) and let S be a neighbourhood of the origin. The closed-loop trajectory xCL(·) is said to be uniformly ultimate bounded (UUB) in S if for all μ >0 there exist T(μ)>0 and u(t)∈U such that, for every‖x(0)‖≤μ, xCL(t)∈S for all t ≥T(μ).
Definition 4: Given a set S ⊆Rn, I n[S]⊆S denotes its inner convex approximation.
Definition 5: Given a set S ⊆X×Y ⊆Rn×Rm, the projection of S onto X is defined as ProjX(S):={x ∈X|∃y ∈Y s.t.(x,y)∈S}.
Definition 6: Given a finite set W, card(W) denotes its cardinality.
Definition 7: Given sets A,B ⊂Rn, A ~B:={a: a+b ∈A,∀b ∈B} denotes the Pontryagin-Minkowski set difference.
II. PROBLEM FORMULATION
A. Modeling
Throughout the paper, the class of leader-follower configurations where at least one follower may be linked with more than a single path will be considered, see e.g., the dashed circles of Fig.1. With respect to standard platoon structures this configuration is computationally higher demanding because at each level the action pertaining to a single node could depend on more than an agent. On the other hand, the graph LF topology allows to address more complex scenarios with an increased flexibility level, for example research and rescue tasks in narrowed environments need to acquire information from different points of view [27].
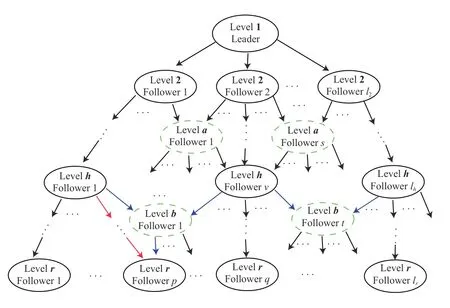
Fig.1. Directed acyclic LF graph topology.
To formally take care of the graph LF topology of Fig.1,hereafter denoted as G, the following operator:
level(i):{1,...,L}→Z+








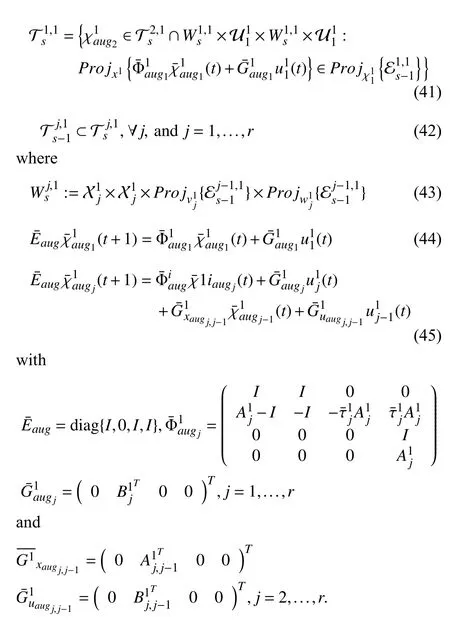
 IEEE/CAA Journal of Automatica Sinica2021年3期
IEEE/CAA Journal of Automatica Sinica2021年3期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Ground-0 Axioms vs. First Principles and Second Law: From the Geometry of Light and Logic of Photon to Mind-Light-Matter Unity-AI&QI
- Deep Learning for EMG-based Human-Machine Interaction: A Review
- Distributed Secondary Control of AC Microgrids With External Disturbances and Directed Communication Topologies: A Full-Order Sliding-Mode Approach
- Deep Learning in Sheet Metal Bending With a Novel Theory-Guided Deep Neural Network
- Autonomous Control Strategy of a Swarm System Under Attack Based on Projected View and Light Transmittance
- Computing Paradigms in Emerging Vehicular Environments: A Review
