Distributed Cooperative Control of Battery Energy Storage Systems in DC Microgrids

Tingyang Meng, Zongli Lin, Fellow, IEEE, and Yacov A. Shamash, Fellow, IEEE

Abstract—The control of battery energy storage systems(BESSs) plays an important role in the management of microgrids. In this paper, the problem of balancing the state-ofcharge (SoC) of the networked battery units in a BESS while meeting the total charging/discharging power requirement is formulated and solved as a distributed control problem.Conditions on the communication topology among the battery units are established under which a control law is designed for each battery unit to solve the control problem based on distributed average reference power estimators and distributed average unit state estimators. Two types of estimators are proposed. One achieves asymptotic estimation and the other achieves finite time estimation. We show that, under the proposed control laws, SoC balancing of all battery units is achieved and the total charging/discharging power of the BESS tracks the desired power. A simulation example is shown to verify the theoretical results.

I. INTRODUCTION

ENERGY storage systems are essential components in microgrids [1]. They not only ensure the power quality and reliability but also reduce energy loss in microgrids.Among various energy storage technologies, battery energy storage systems (BESSs) have emerged as an appealing technology due to their versatility, rapid response, high energy density, and efficiency [2]. By absorbing power from the grid during off-peak time and supplying power to the grid in peak time, BESSs enable the grid to have the ability of peakshaving/shifting, power quality enhancement, and congestion relief [3]. As a result, BESSs of various types are increasingly being integrated into modern energy systems [4], [5]. Despite the technological advancements in electrochemistry, management/control of BESSs remains a challenging problem [6].

In general, a BESS may be composed of multiple battery units. Each unit monitors its own state and controls its own charging/discharging power while communicating with nearby units. The fundamental control objective of a BESS is to satisfy the charging/discharging power desired by the grid while balancing the state-of-charge (SoC) of all its units. Due to variations in their manufacturing process and in their operating conditions, battery units may exhibit different characteristics even if they have the same nominal specifications. As a result, the SoC of all battery units may diverge with the same charging/discharging power. The divergence of their SoC can eventually lead to overcharge/overdischarge of the units, which significantly reduces not only the efficiency of the system but also the lifetime of battery units, and may even cause dangerous situations.Therefore, the design of coordinated control of charging/discharging power for the units in a BESS with SoC balancing has been an active research problem (see, e.g., [7]-[11]).

The control scheme of a BESS consisting of networked battery units can be either centralized or distributed. A centralized controller monitors all battery unit’s SoC and other critical states, and coordinates the charging/discharging power of each individual unit by external balancing circuits [12].Such centralized control schemes for large-scale systems are costly to implement and can introduce single-point failures. In addition, the balancing circuits may introduce circulating currents that cause energy loss. Distributed control schemes,on the other hand, provide advantages such as robustness and reconfigurability. Models such as multi-agent systems match the networked structure of battery units in BESSs. Thus, the control problem of a BESS can be reformulated in the framework of multi-agent systems (see, e.g., [13]-[19]), in which the battery units are regarded as a group of locally interacting agents. Distributed controllers and estimators can be designed by using local information and communication among neighbors so that the desired power is satisfied while SoC balancing of all units is achieved.

In particular, in [7], a distributed control scheme for package-level SoC balancing of BESSs is proposed, in which the local power reference for each battery package is generated by an average desired power estimator and an energy coordinator. In [8], a sliding mode control based SoC balancing strategy among multiple BESSs, with each BESS as a battery unit, is proposed under which fast SoC balancing is achieved and circulating currents are prevented. In [9], a distributed two-level controller is proposed, in which the upper-level provides power reference based on SoC and the lower-level controls BESSs to track the power reference. In[10], with the desired total charging/discharging power known to each BESS in a group of networked BESSs, each representing a battery unit, the charging/discharging power of each BESS is assigned based on the average of the states of the BESSs that contain both intrinsic properties as well as the SoC of the BESSs. Event-triggered design is adopted to reduce unnecessary communication loads. Simulation results demonstrate that, in the event that the average of the states of the BESSs is not accessible to all individual BESSs and needs to be estimated by distributed average state estimators, the controllers are able to achieve the control objective approximately despite of the estimation errors.

In this paper, we design distributed controllers for a BESS consisting of multiple networked heterogeneous battery units.A novel control framework based on distributed estimators is proposed that only requires the, possibly time-varying, desired charging/discharging power to be known by at least one of the battery units. The SoC of all battery units is balanced through the charging/discharging process by allocating the desired total charging/discharging power of the entire BESS among its units. A distributed allocating/control algorithm is designed for each battery unit based on the distributed estimators built for the battery unit that estimate the average desired charging/discharging power and the average unit state. These estimators are referred to as the average desired power estimators and the average unit state estimators, respectively.Compared to the existing results in [10], we provide explicit analysis of the effects of estimation errors on control accuracy. We show that, by setting the design parameters properly, the desired charging/discharging power can be satisfied and SoC balancing can be achieved by any prespecified accuracy. In addition, we propose alternative finitetime estimators that can achieve perfect power supply and SoC balancing.

The remainder of the paper is organized as follows. Section II reviews graph theory that is used to describe the communication network. Section III formulates the control problem of a networked BESS, including desired charging/discharging power tracking and SoC balancing. Section IV recalls charging/discharging power allocating algorithms by using the desired charging/discharging power and the average unit state.Section V presents distributed charging/discharging power controllers based on asymptotic average power estimators and average unit state estimators. Section VI presents charging/discharging power controllers based on finite-time average power estimators and finite-time average unit state estimators.Section VII provides simulation results to verify and compare the theoretical conclusions. Section VIII concludes the paper.

II. GRAPH THEORY

III. PROBLEM STATEMENT

In this paper we consider a BESS consisting of N networked battery units. Each battery unit, with its own distributed controller, is able to communicate with nearby battery units and exchange critical states such as their SoC so that the overall control objective of the networked system can be achieved.

We make the following assumption on the communication topology among the battery units in the BESS.

Assumption 1: The graph associated with the communication topology is undirected and connected.

Under Assumption 1, the graph Laplacian L is symmetric with eigenvalues 0=λ1＜λ2≤λ3≤···≤λN. In addition, 1Nis the eigenvector associated with λ1=0 [13].

The following well known Coulomb counting method is used to model the SoC dynamics of each battery unit,

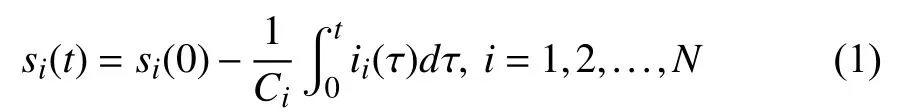
where si(t) is the SoC at t ≥0 , si(0) is the initial SoC value, Ciis the capacity, and ii(t) is the output current. The output current ii＞0 indicates discharging and ii＜0 indicates charging. By taking the time derivative of both sides of (1),the SoC dynamics of each battery unit is given as

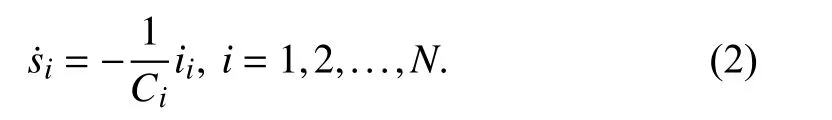
The output power pi(t) of each battery unit is calculated as

where vi(t) is the output voltage. The output power pi＞0 indicates discharging and pi＜0 indicates charging. It is noted that most direct current to direct current (DC-DC)bidirectional converters commonly used in BESSs have a constant output voltage [20]. Thus, in this paper we assume that the output voltage of each battery unit remains constant during its operation, i.e.,

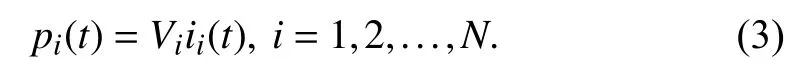
Since the state of the BESS will remain unchanged with zero charging/discharging power demand, we will, without loss of generality, make the following assumption on the desired total power.

Assumption 2: The desired total charging/discharging power p*(t) of the BESS satisfies

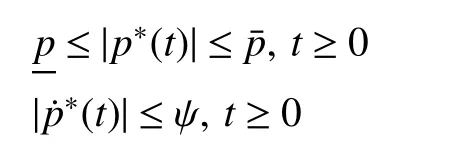
for some positive constants p, p¯ and ψ.

The control objective of the BESS is stated as follows.

Problem 1: Consider a BESS consisting of N networked battery units with SoC dynamics (2) and output power equation (3). Let the communication topology satisfy Assumption 1. Let the desired total power satisfy Assumption 2.Design distributed charging/discharging power controllers for the battery units so that

1) all units achieve SoC balancing with any pre-specified accuracy εs≥0 in steady state, i.e.,

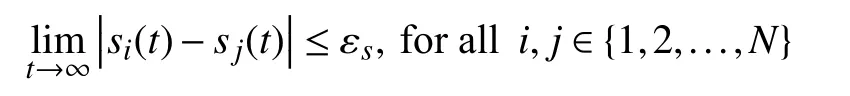
2) the total charging/discharging power of the BESS tracks the desired power with any pre-specified acuracy εp≥0, i.e.,

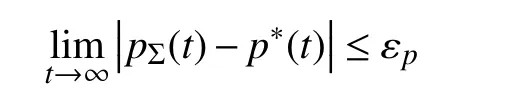
IV. POWER CONTROL BASED ON THE AVERAGE UNIT STATE

In this section, we first recall the SoC variation rules for the battery units based on their SoC, then recall power allocating laws based on the average state of all units [10].

Consider the SoC dynamics (2) and output power equation(3) for each BESS (battery unit). The relationship between the SoC si(t) and the output power pi(t) of the i-th battery unit is written as

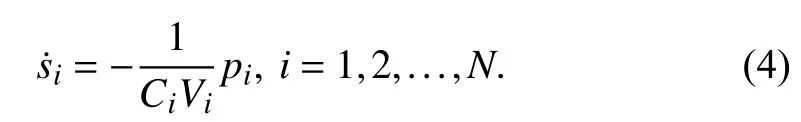
It is noted that, by properly distributing the desired total output power p*(t) among individual battery units based on their SoC, capacity and voltage, the SoC balancing can be achieved during the charging/discharging process.

In [10], the authors proposed the following rules to regulate the SoC variation during the charging/discharging process:

1) In discharging mode

2) In charging mode

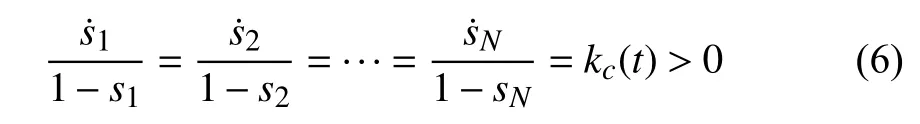
where kd(t) and kc(t) are some functions lower bounded by a positive number and satisfying the power demand. In other words, during the discharging process, a battery unit with higher SoC discharges at a higher rate while a unit with lower SoC discharges at a lower rate. The similar principle holds for the charging process.

Lemma 1 [10]: Consider a BESS consisting of N networked battery units with SoC dynamics described by (2). Under discharging/charging rules (5) and (6), the SoC of all battery units will converge to the same value asymptotically.

Next, we recall power control laws that specify the charging/discharging power of individual battery units [10].

For each battery unit i, i =1,2,...,N, define the state

for the discharging mode, and

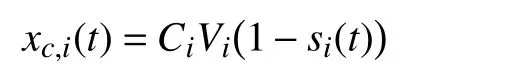
for the charging mode. The overall state of the battery unit i is denoted as

In view of (4), we have

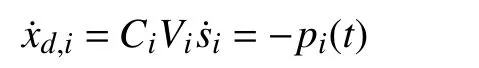
for the discharging mode, and

for the charging mode.

Since

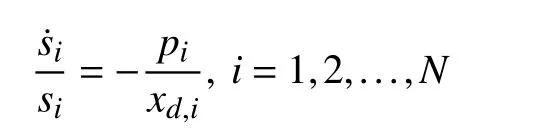
for the discharging mode, and

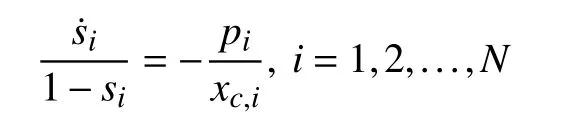
for the charging mode, the charging/discharging power of all battery units must satisfy

for the discharging mode, and

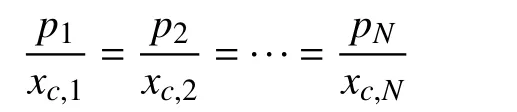
for the charging mode.

Design the charging/discharging power of each battery unit as

for the discharging mode, and

for the charging mode.

Then, it is straightforward to verify that both the SoC balancing and the desired total power is satisfied. Denote the average unit state as

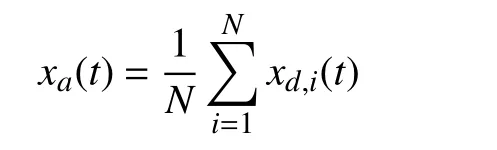
for the discharging mode, and

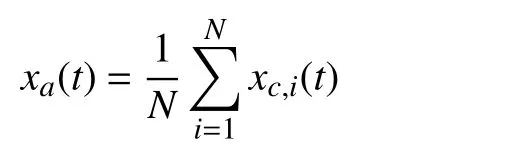
for the charging mode. Denote the average desired power as

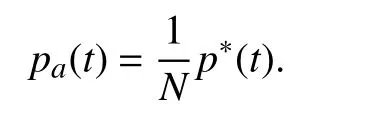
Then, (7) and (8) can be written as

Assumption 3: There exist constants a1, a2＞0 such that

The discharging power of each battery unit i in steady state is written as

Then, in steady state, we have

Define

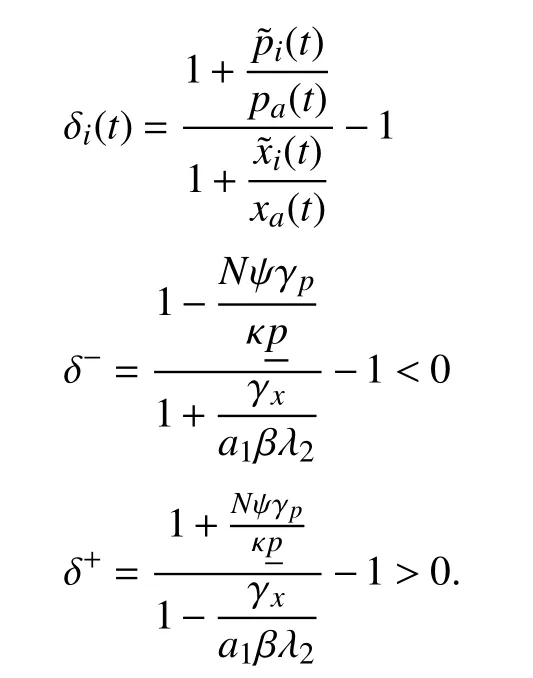
Then, in steady state, we have

δ－≤δi(t)≤δ+.

In addition, the bound can be made arbitrarily tight by choosing the parameters β and κ sufficiently large.

Define

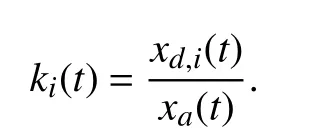
Then, (12) can be rewritten in terms of k (t) and δi(t) as

pi=k(1+δi)ˆpa,i.

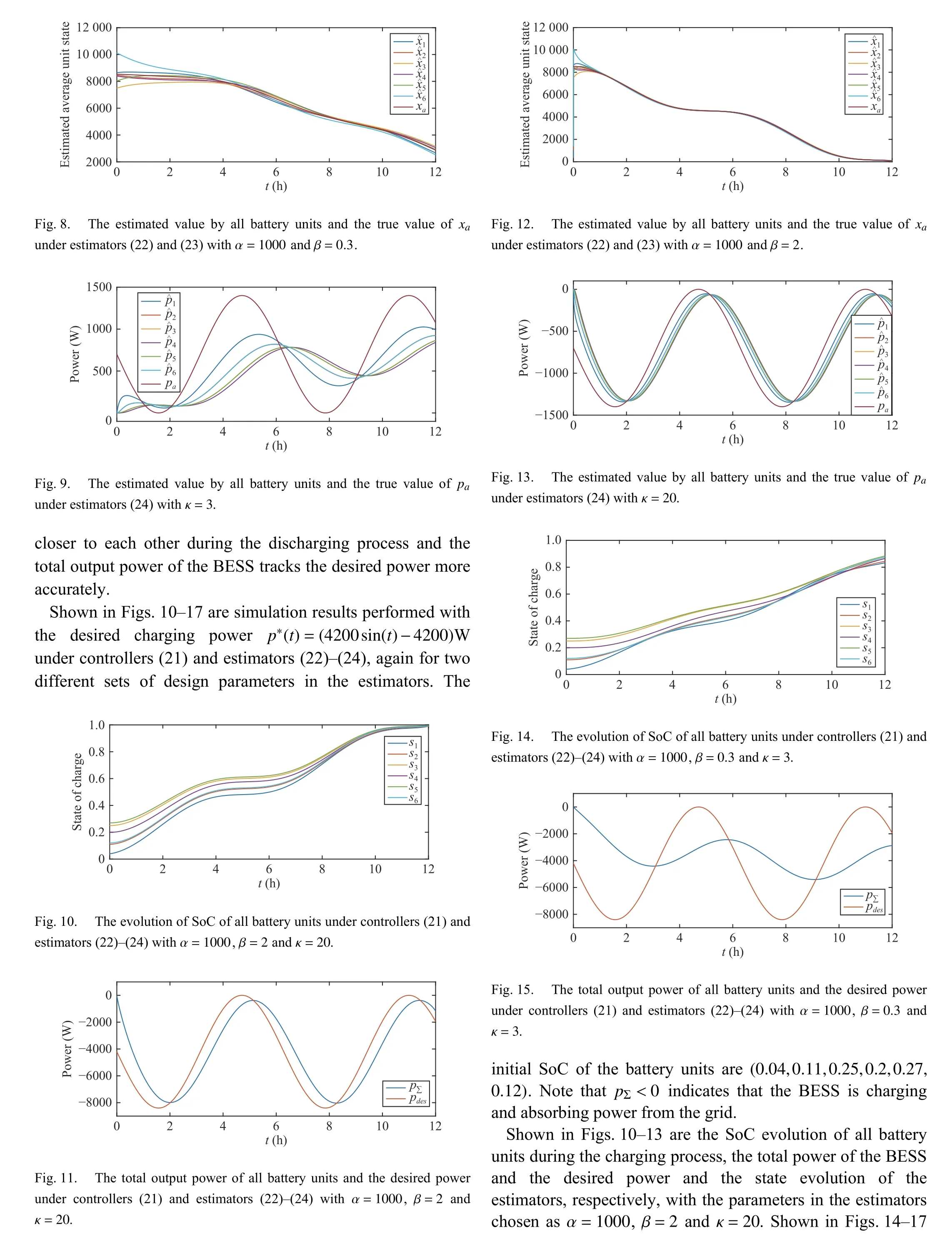
Fig.2. The evolution of SoC of all battery units under controllers (21) and estimators (22)-(24) with α =1000 , β =2 and κ =20.

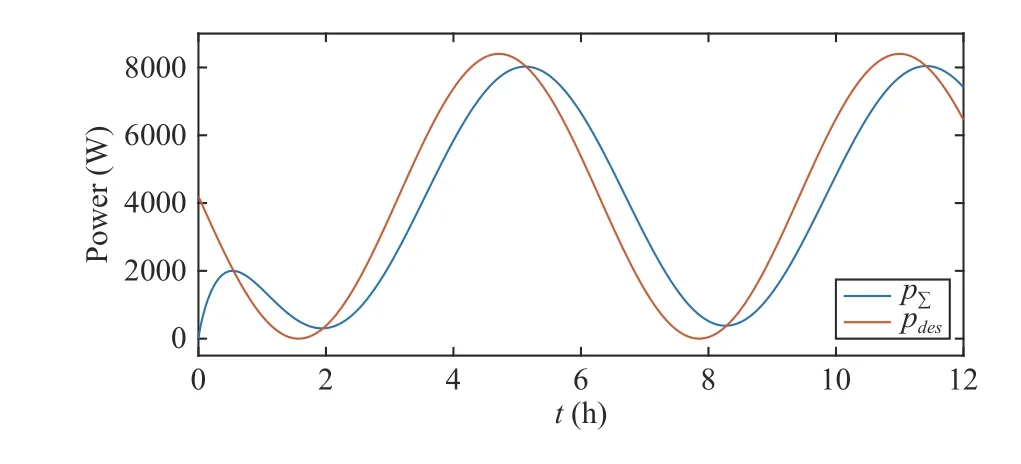
Fig.3. The total output power of all battery units and the desired power under controllers (21) and estimators (22)-(24) with α=1000 , β=2 and κ=20.

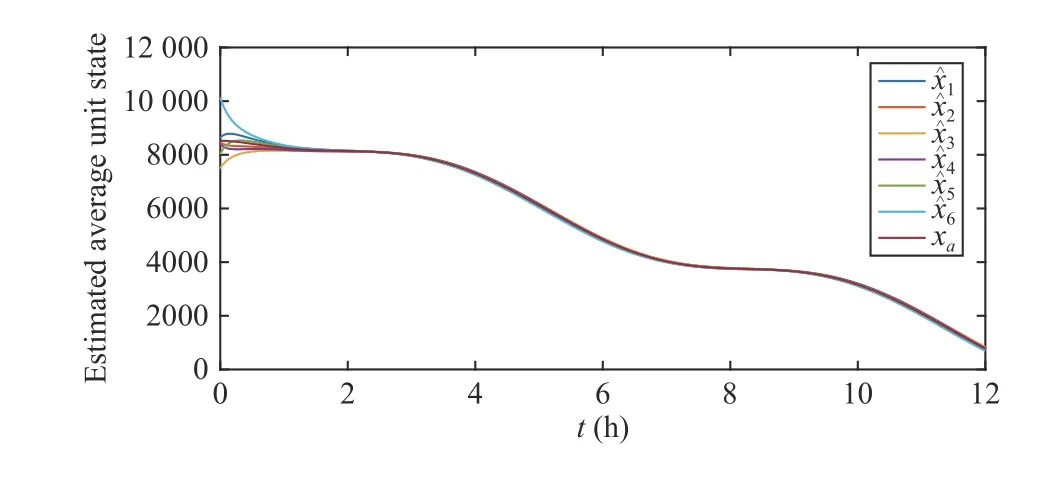
Fig.4. The estimated value by all battery units and the true value of xa under estimators (22) and (23) with α =1000 and β =2.

Fig.5. The estimated value by all battery units and the true value of pa under estimators (24) with κ =20.

Fig.6. The evolution of SoC of all battery units under controllers (21) and estimators (22)-(24) with α =1000, β =0.3 and κ =3.

Fig.7. The total output power of all battery units and the desired power under controllers (21) and estimators (22)-(24) with α=1000 , β=0.3 and κ=3.

VIII. CONCLUSIONS

In this paper, we consider a BESS consisting of networked battery units and present a distributed control design based on distributed average unit state estimators and distributed average desired power estimators. We show that, by choosing the design parameters properly, the proposed two types of distributed estimators can estimate the average signals with