装备剩余寿命预测与维修保障策略研究

顾曦文，温 瑞，吴 琦

（91351 部队）

0 引 言

传统的装备维修保障通常根据大量装备损伤或寿命的历史统计规律配置大量的维修保障资源并指导维修保障实践，由于缺乏对装备个体技术状态的准确判断，致使难以对维修保障需求进行实时准确的预计，同时各层级维修保障资源之间缺乏灵活的协同机制，致使整个维修保障体系中经常面临局部维修保障能力过剩或不足的情况，传统装备维修保障呈现费用高、效能低的特点。装备自主维修保障与感知响应保障理念强调以网络为中心，结合故障预测健康管理技术与分布式决策技术， 通过实时获取维修保障需求、动态配置保障资源来提高装备可靠性， 缩减保障规模，降低保障费用与保障风险[1-3]。

实现装备自主维修保障 （Autonomic Logistics System，ALS）需要两个关键要素（维修保障需求的准确预测能力和全局范围内动态响应维修保障需求）来重构维修保障资源的决策能力。有些学者在相关方面作了一些探索，如文献[3-5]分析了装备故障预测信息与备件库存策略以及供应链的关系， 并提出了相应的单部件系统换件维修模型与供应链优化设计模型；文献[6]采用复杂网络理论与方法构建了基本的自适应保障的网络模型，并对重要的特征参数进行了统计分析与对比。 整体来说，目前关于装备维修决策、备件管理、资源分配的研究相对比较多，但其理论系统均建立在传统的维修保障体制与模式基础之上。为了适应网络化作战及精确保障的要求，特别需要对将装备故障预测信息与维修保障网络深度结合的自主维修保障体系进行研究。

本文针对上述存在的问题以武器装备管理过程的实际情况为例， 提出了一种新的装备剩余寿命预测与维修保障策略。 采用神经网络模型及遗传算法求解了在该情况下最优的装备剩余寿命预测与维修保障策略。 分析该类装备关键部件寿命分布的规律性，预测分析其相应的剩余寿命，并根据该类装备关键部件更换与库存的相关数据， 在保证部件可靠度不低于要求的条件下，研究其最佳的更换时间、备件订购时间和订购数量，使得总费用最低，最终针对该类装备，制定一个长期的、最经济与可信度高的维修保障策略。

1 装备失效函数

在武器装备管理中，定期对其关键部件的综合性能指标X 进行检测，间隔时间为15 天。 当综合性能指标X 达到失效阈值ω=0.7 时，则认为该部件寿命终止。

首先根据之前储存的装备信息部件为样本，认为性能指标X 为随机变量， 计算其在不同时刻性能指标随机变量AXj 内元素满足的分布。 以此为基础，求解不同时刻性能指标X 大于失效阈值ω 的概率，得到部件失效分布函数。

由于不同时刻部件的性能指标符合正态分布，但是不同时刻， 性能指标符合的正态分布的参数不相同。 对于已知的162 个不同时刻的参数AXj，正态分布参数μj，σ2j的估计值如图1 所示。

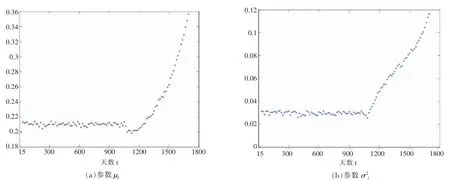
图1 正态分布参数μj、σ2j在不同时刻估计值

由于j 时刻的正态分布参数μj，σ2j都是在离散状态下的估计值。 对于可靠性指标的分布函数X(t)，需要求解在连续情况下可靠性指标X 服从的分布函数，即装备失效函数。

本文采用对离散的估计参数μj，σ2j拟合的方法将离散的参数连续化。 使用多项式拟合估计参数μj，σ2j的变化，当多项式次数较高时，可以得到较好的拟合结果。然而当时间变量超过被拟合数据中所给的范围后， 高阶多项式拟合结果可能出现很大的振荡，这是高阶多项式拟合的最大问题。为了避免拟合函数在后期的发散，我们尽量使用三阶以下的多项式进行拟合。 鉴于参数μj，σ2j随时间的变化比较复杂，三阶以下的多项式很难较好的拟合情况，本文对参数μj，σ2j进行分段， 分别用分段函数进行拟合。 用MATLAB的cftool 曲线拟合工具箱， 对分段的参数μj，σ2j进行拟合：

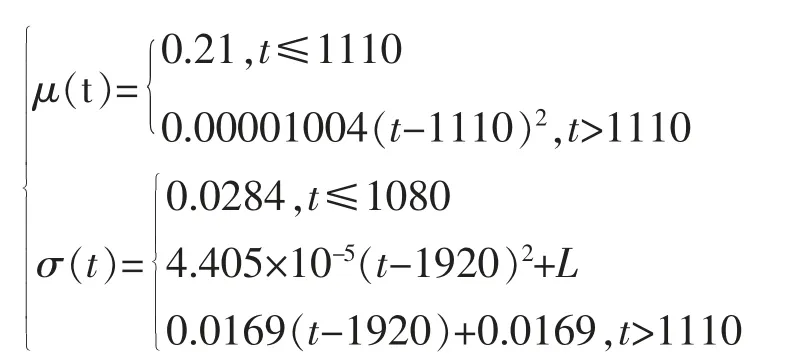
拟合函数如图2 所示。

图2 正态分布参数μj、σ2j的拟合

则部件失效的概率分布函数F（t）可表示为:

2 装备寿命预测

可通过上述已知的观测样本中得出的寿命规律，来预测现存20 个装备的剩余寿命。

由于整个性能指标退化过程视为马尔科夫过程，只需将20 个部件给出的最后性能指标值和对应天数，即可和之前的数据相对比，通过聚类算法将20 组数据归类， 得出此题中20 个部件所属的剩余寿命分布规律（见图3），利用相应类型的分布规律得到剩余寿命，进而得到可信度。

图3 20 个部件剩余寿命Y 分布函数图

采用聚类方法， 当得到相应的数据组类型后，读取同一类型内的参考数据组的部件寿命，即检测数据ω>0.7 的时间T。 将参考数据组的部件寿命T 与对应待求数据组作差，得到该类型部件在128 次检测后的剩余寿命所呈现特征， 经过分析拟合，不同待求组所分类型得到的剩余寿命Y 均服从正态分布。

3 装备存储方案

本文通过假设，将装备储存方案变为一个线性规划问题求解。 由部件剩余寿命分布函数，求得各部件在每一天的失效概率。将20 个部件的订货时间、更换时间作为变量，求解在约束条件下，使与其费用最低时， 变量的最优取值， 从而确定20 个部件的订货时间、每次订购数量和部件更换时间，得到最优方案。

为了简化问题，本文对实际情况做如下假设：

1） 各个部件每个只需要更换一次。

2） 每个部件有且仅有一个指定备件， 且备件相互之间不可混用。

3） 不到方案规定的更换时间， 即使部件失效且有备件，也不进行更换。

4） 费用最低指单位使用时间上费用最低。

本文将决策问题转化为线性规划问题。

记20 个部件的订货时间为TD1，TD2， …，TD20，20个部件的更换时间为TH1，TH2，…，TH20。 记进货次数为n，每一次进货数量为N1，N2，…，Nn。

由于部件购买价格固定，在前述的假设中已规定只购买20 个备件，这部分花费大小是固定的，可以不予以考虑。

记部件i 所花费的所有花费期望为fi， 在单位使用时间下，部件花费期望为。定义总费用ftotal为所有单位时间花费与订货费用之和的期望，有

将20 个部件的订货时间TD1，TD2，…，TD20以及更换时间TH1，TH2，…，TH20作为线性规划的决策变量。 即决策变量共有40 个。

目标函数为

由于需要优化的参数多达40 个， 而且参数间相互影响，仅用普通的线性规划方法难以得到优化结果并进行比较分析。为此，选用遗传算法，以快速求解模型的近似最优解。

遗传算法是一种采用生物进化理论进行选择问题的近似最优解的方法。 它具有不要求函数连续、可扩展性、潜在的并行性等优点，已得到了广泛的运用。它的实施过程包括编码、产生初始种群、计算适应度、选择、复制、交换、突变、反复迭代、终止等操作。

本文使用Matlab 自带的遗传算法库函数ga（）进行求解。 设定种群大小为100，演化1000 代，染色体交叉的概率为0.8，染色体变异概率为0.05。在约束条件下，优化的目标函数，使得总费用期望值最低。对这些参数进行编码并仿真，得到的结果（仿真求解的结果为小数，将其向下取整，取值为整数天数）如下：

订购次数n=4 次， 分别在第974 天、1184 天、1401 天、1610 天进行订货。

4 维修策略

本文采用周期性视情检测策略，即在离散时间点tk=kΔt（k∈N）进行检测，Δt 为固定的检测时间间隔，检测后可获得各个部件的实际退化量， 可根据F（t）计算得到各部件的剩余寿命Y。维修的首要目的是减少非计划故障，因此，在tk，时刻进行检测时，部件i的剩余寿命Yi必须大于检测时间间隔Δt， 以用来避免下一个检测间隔期内出现故障。同时，根据Yi的大小确定是否进行预防性更换，即在tk，时刻进行检测时， 如部件i 的剩余寿命Yi小于预设的剩余寿命阈值tpr（tpr≥Δt）时，则进行预防性更换，所需要费用为Cpr；如部件在(tk-1，tk)期间发生了故障，则在tk时刻对其进行修复性更换，所需费用为Cf，(Cf>Cpr)，以上维修策略实施的前提条件是有备件可用。

（S，s）策略是目前比较通用的备件策略，即仓库内能存放的最大备件数S， 当备件数下降到s 时，发出订购S-s 个新备件的指令。假设备件单位时间的库存持有成本为Ck，备件存放在仓库里不会劣化。 每个备件购买的成本为Cpart，备件从发出订购订单到到达仓库的时间间隔为交付时间t。 目前的(S，s)备件策略较为被动，只在备件被消耗到一定程度后才会发起订购，由于购买的备件需要t，的时间才能到达，一些复杂关键部件的交付时间甚至长达数周，如果交付时间内， 多个同类型部件需要进行预防性或修复性维修，较低的安全库存量很可能就无法应对。而维持较高的库存则需要长期支付高昂的库存费用。 为此，本文在维修决策与备件库存量优化的基础上，还采用了备件预约的概念， 即当部件的剩余寿命下降到一个阈值时，该部件可向库房预约一个备件，此时该备件就被该部件锁定。 除非有部件出现故障且无备件使用时，否则该备件仅供被预约的部件使用。相应的备件策略可优化为：若cs-bs≤s，则发出订购备件订单，其中cs为当前备件库存量，bs为被预约的库存量。

根据维修决策与备件库存量联合策略的分析可知，联合优化的目标是在保证安全的条件（即Δt≤tpr）下，使得无限时间范围内系统维修和备件总成本的平均费用率到达最低，需优化的参数有：剩余寿命阈值t，预约备件的时间阈值tpr和库存参数S，s。 因此，优化模型可以描述为

式中，fEC∞（Δt，tpr，t，S，s）为平均费用率函数。 由于需要优化的参数多，而且参数间相互影响，仅用蒙特卡罗方法难以得到优化结果并进行比较分析。 为此，选用遗传算法和蒙特卡罗仿真相结合的方法，以快速求解模型的近似最优解，论文给出的联合优化模型的求解流程如图4、图5 所示。

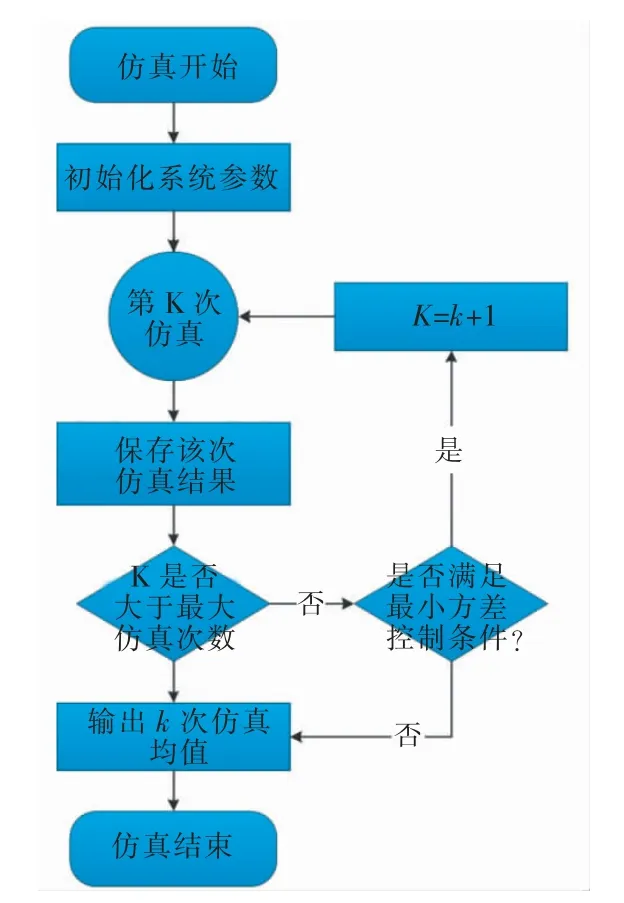
图4 总体仿真流程

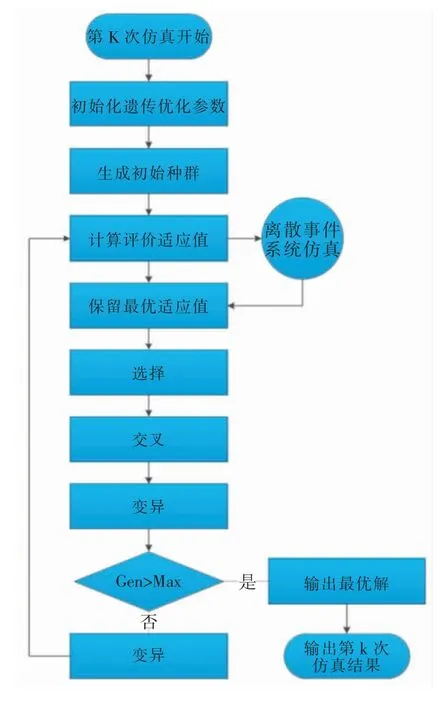
图5 第K 次仿真流程

根据模型求解可得，得到长期最经济且可信度较高的维修策略为：

达到1861 天后，统一更换60 个部件，以此类推，每过1861 天，即更换所有部件，在更换部件前60 天，即订货。 一轮正常更换所需费用20990 万元，可以使用1861 天，部件可靠度为90%。

5 结 论

基层部队装备多，技术复杂，维修决策的内容多、难度大。采用装备维修策略决策技术可以充分利用已有维修信息和故障知识，从而制定出科学的维修策略，为故障装备的维修缩短时间，降低费用；为基层部队制定科学的维修大纲提供依据。本文在国内外维修策略技术相关研究的基础上，利用功能分析方法，建立了装备维修策略决策的功能模型，划分出了装备维修策略决策的功能模块。结合某装备中的维修策略的具体实现，以装备故障模式、影响分析和故障分布模型分析为决策的基础，研究了装备维修方式和（S，s）、维修级别及维修次序的决策，较好地实现了装备维修方式、维修间隔期、维修次序、维修级别的决策，并取得了初步应用效果。