Data-Based Optimal Tracking of Autonomous Nonlinear Switching Systems

Xiaofeng Li, Lu Dong, Member, IEEE, and Changyin Sun, Senior Member, IEEE

Abstract—In this paper, a data-based scheme is proposed to solve the optimal tracking problem of autonomous nonlinear switching systems. The system state is forced to track the reference signal by minimizing the performance function. First,the problem is transformed to solve the corresponding Bellman optimality equation in terms of the Q-function (also named as action value function). Then, an iterative algorithm based on adaptive dynamic programming (ADP) is developed to find the optimal solution which is totally based on sampled data. The linear-in-parameter (LIP) neural network is taken as the value function approximator. Considering the presence of approximation error at each iteration step, the generated approximated value function sequence is proved to be boundedness around the exact optimal solution under some verifiable assumptions. Moreover, the effect that the learning process will be terminated after a finite number of iterations is investigated in this paper. A sufficient condition for asymptotically stability of the tracking error is derived. Finally,the effectiveness of the algorithm is demonstrated with three simulation examples.

I. INTRODUCTION

THE optimal scheduling of nonlinear switching systems has attracted vast attention in recent decades. A switching system is a hybrid dynamic system which consists of continuous time subsystems and discrete time events. For each time step, only one subsystem is selected so that the main issue is to find the optimal policy to determine “when” to switch the mode and “which” mode should be activated [1],[2]. Many complex real-world applications can be described as switching systems, ranging from applications in bioengineering field to electronic circuits [3]-[7].

Generally, the existing methods for optimal switching problem can be classified into two categories. The methods belonging to the first category are to find the switching sequence in a “planning” manner. In [8]-[11], nonlinear programming based algorithms are designed to determine the switching instants by using the gradient of the performance function. Note that the sequence of active modes are required to be fixed a priori. In [12], the authors propose a two-stage decision algorithm to allow free mode sequence which distinguishes the decision process of active mode and switching time. On the other hand, discretization-based methods solve the problem by discretizing the state and input space with a finite number of options [13]-[16]. However,these planning based algorithms achieve good performance only with specific initial states. Once the given initial conditions are changed, a new planning schedule should be made from the scratch.

Optimal control is an important topic in modern control theory which aims to find a stabilized controller which minimizes the performance function [17]. In recent years,researchers have developed many optimal schemes for addressing practical real-world applications, such as trajectory planning and closed loop optimal control of cable robots[18]-[20]. Based on the reinforcement learning mechanism,the adaptive dynamic programming (ADP) algorithm was first developed to solve the optimal control problem of discretetime systems with continuous state space [21], [22]. In parallel, a continuous-time framework was proposed by the group of Frank L. Lewis to extend the application of ADP to continuous-time nonlinear systems [23]-[25]. Two main iterative methods including value iteration (VI) [26] and policy iteration (PI) [27] are employed to solve the Hamilton-Jacobi-Bellman (HJB) equation. The actor-critic (AC)structure is often employed to implement the ADP algorithm with two neural networks (NNs) [28]. The critic network takes system states as input and outputs the estimated value function while the actor network approximates the mapping between states and control input [29].

According to the requirement of system dynamics, the family of ADP algorithms can be divided into three main aspects, including model-based methods, model-free methods,and data-based methods. The model-based ADP algorithms require we know the exact dynamics of the plant [26], [27],[30]. A monotonous non-decreasing or non-increasing sequence of value function is generated VI or PI based algorithm which will converge to the optimal solution. For the model-free algorithms, the system model is first identified,e.g., by using neural network (NN) or fuzzy system. Then, the iterations are operated based on the approximated model [31],[32]. It is worth noting that the presence of identification error may lead to sub-optimality of the learned policy. In contrast to the above two approaches, data-based ADP methods are totally based on input and output data [33]-[37]. The objective is to solve the Q-function based optimal Bellman function so that the optimal controller can be obtained without knowing system dynamics. Recently, the combination of ADP method with event-trigger mechanism has been investigated which substantially reduces the updating times of the control input without degrading the performance [38]-[41]. Considering the uncertainty of the system dynamics, the robust ADP algorithms are proposed to find the optimal controller of practical applications [42], [43]. In addition, many practical applications have been solved successfully by using the ADP method [44]-[46].

As a powerful method for solving the HJB equation, ADP has been applied to solve the optimal control of switching systems in recent years. In [30], the optimal switching problem of autonomous subsystems is solved by using an ADP based method in a backwards fashion. In addition, the minimum dwell time constraint between different modes is considered in [47]. The feedback solution is obtained by learning the optimal value function with respect to the augmented states including system state, already active subsystem, and the elapsed time a given mode. In order to reduce the switching frequency, a switching cost is incorporated in the performance function [48]. In [49], the optimal tracking problem with infinite-horizon performance function is investigated by learning the mapping between the optimal value function and the switching instants. For the continuous-time autonomous switching system, a PI based learning scheme is proposed with consideration of the effect of approximation error on the behaviour [50]. Moreover, the problem of controlled switching nonlinear systems is addressed by co-designing the control signal and switching instants. In [51], the authors develop a VI based algorithm for solving the switching problem. Since a fixed-horizon performance function is considered, the optimal hybrid policy is obtained backward-in-time. In [52], the optimal control and triggering of networked control system is first transformed to an augmented switching system. Then, an ADP based algorithm is proposed to solve the problems with zero order hold (ZOH), generalized ZOH, finite-horizon and infinitehorizon performance functions. These aforementioned methods provide the closed-form solution which works for a vast domain of initial states. However, it is worthwhile noting that the accurate system dynamics is required to implement the existing algorithms which is difficult to obtain for complex nonlinear systems. In addition, the effect of approximation error incurred by employing the NN as the value function approximator is often ignored in previous literature.

In this paper, a data-based algorithm is first proposed to address the optimal switching problem of autonomous subsystems. Instead of the requirement for system model, only input and output data is needed to learn the switching policy.Furthermore, two realistic issues are considered in this paper.On the one hand, the effect of presence of approximation errors between the outputs of a NN and the real target values are investigated. On the other hand, a sufficient condition is derived to guarantee the stability of the tracking error with a finite number of iterations. In addition, the critic-only structure is utilized for implementing the algorithm. The main contributions of this paper are listed as following. First, the problem is transformed to solving the Q-function based Bellman optimality equation, which enables us to derive a data-based algorithm. Second, considering the approximation errors, an approximated Q-learning based algorithm is first proposed for learning the optimal switching policy. Finally,the theoretical analysis of continuity of Q-functions,boundedness of generated value function sequence and the stability of the system is presented. Since [50]-[52] are all model-based methods, the completely “model-free” character of the proposed algorithm demonstrates its potential for complex nonlinear systems.

The rest of this paper is organized as follows. Section II presents the problem formulation. In Section III, the exact Qlearning algorithm is proposed. Then, the approximated method is derived considering approximation error and a finite number of iterations. In addition, a linear-in-parameter (LIP)NN is utilized for implementing the algorithm of which the weights are updated by using least-mean-square (LMS)method. In Section IV, the theoretical analysis is given.Afterwards, three simulation examples are given in Section V.The simulation results demonstrate the potentials of the proposed method. Finally, conclusions are drawn in Section VI.

II. PROBLEM FORMULATION

Hence, the tracking problem is transformed to find the optimal Q-function. In the next section, an iterative Q-learning based algorithm is developed. In addition, the effects of the presence of the approximation error as well as termination condition of iterations are considered.

III. PROPOSED ALGORITHM AND ITS IMPLEMENTATION

A. Exact Q-Learning Algorithm

It is worth noting that the convergence, optimality, and stability properties of exact Q-learning algorithm is achieved based on several ideal assumptions. On the one hand, the exact reconstruction of the target value function (15) is difficult when using value function approximators, except for some simple linear systems. On the other hand, theoretically,an infinite number of iterations are required to obtain the optimal Q-function. In the following subsection, these two realistic issues are considered and the approximated Qlearning algorithm is developed.

B. Approximated Q-Learning Algorithm

The approximated Q-learning method is proposed by extending the exact Q-learning algorithm. First, the algorithm starts from a zero initial Q-function, i.e., Qˆ(0)=0. Afterwards,considering the approximation error, the algorithm iterates between

C. Implementation

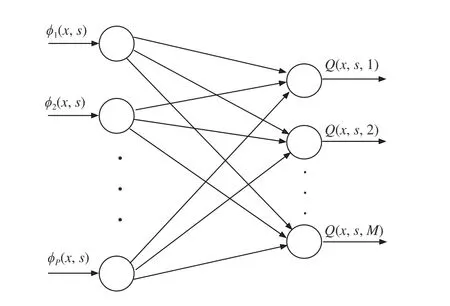
Fig. 1. The structure of critic network. The LIP NN consists of a basis function layer and a output layer. The basis functions are polynomials of combinations of system states and reference signals while the number of nodes is determined by trial-and-error method and the output layer has M nodes.

The output of critic network can be expressed by can be updated at each iteration.

Fig. 2. Simple diagram of the proposed algorithm. This figure shows the weight update process of an arbitrary output channel. The target network shares the same structure and weights of the critic network and computes the minimum value of Q-function at next time step. Note that at each iteration step, the weights of all output nodes should be updated.

Another critical problem is to select the appropriate termination criteria for the training process. Let the iteration be stopped at the j-th iteration if the following convergence tolerance is satisfied

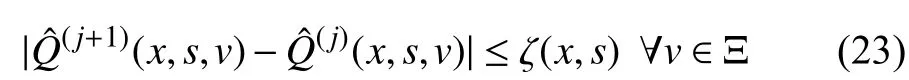
where ζ(x,s) is positive definite function. Once the Q-function Qˆ(j)(x,s,v)is obtained, it can be applied to control system (1)by comparing the values of different modes and selecting the optimal one. The main procedure for implementing the proposed algorithm is given as in Algorithm 1. The theoretical analysis of the effect caused by the termination condition is given in the following section.

Algorithm 1 Outline of Implementation of the Proposed Algorithm Step 1: Initialize the hyper-parameters including number of sampled data L and the termination condition of training process .ˆW(0)c,v =0 8v Ξ ζ Step 2: Initialize the weight vector of the critic NN, i.e.,.�x[l]k Ωx,s[l]k Ωs,v[l]k Ξ�L l=1 L Step 3: Randomly select a set of sample data, where is a large positive integer.�x[l+1]k ,s[l]k+1�L s[l]k+1=F(s[l]k )l=1 x[l]k+1= fv[l]k (x[l]k )Step 4: Obtain according to and, respectively.j=0 Step 5: Let and start the training process.Step 6: The active mode at next time step is selected according to.v(j),[l]k+1 =argminv Ξ(ˆW(j)c,v)Tφ(x[l]k+1,s[l]k+1)ˆQ(j+1)tar (xk,sk,vk)Step 7: The target values for critic network is computed according to (22). Then, the weights of the LIP NN are updated by using LMS method.j ˆW(j+1)c,v - ˆW(j+1)c,v j ≤ζ 8v Ξ j= j+1 Step 8: If is satisfied, then, proceed to Step 9, otherwise, let and execute Step 6.W∗c,v= ˆW(j)c,v 8v Ξ Step 9: Let and stop the iteration process.

Remark 3: Note that the training process in Algorithm 1 is totally based on input and output data of subsystems. Once the weights of critic network are converged, the control signal can be derived only based on current system state and reference signal. In order to achieve competitive performance, it requires more training data than the model-based and modelfree algorithm. However, collecting input and output data is often easier than identifying the model.

IV. THEORETICAL ANALYSIS

In this section, the effects of presence of approximation error and termination condition on the convergence and stability properties are analyzed. Before proceeding to the proof of theorems, an approximated value function based ADP method is first briefly reviewed [47].

A. Review of Approximated Value Iteration Algorithm

B. Continuity Analysis

C. Convergence Analysis

Next, we will derive the proof that given an upper bounded constraint of approximation error at each iteration, the

D. Stability Analysis

V. SIMULATION RESULTS

In this section, the simulation results of two numerical examples are first presented to illustrate the effectiveness of the proposed method. In addition, a simulation example of an anti-lock brake system (ABS) is included. The simulation examples are run on a laptop computer with Intel Core i7,3.2 GHz processor and 16 GB of memory, running macOS 10.13.6 and MATLAB 2018a (single threading).

《文心雕龙·章句》作为“安章之总术”早已得到学界的普遍认同，以今天的文艺评论眼光来看，毫无疑问是一篇创作论。但对初中语文教师来说，它也是一篇明晰章句、体悟韵律的鉴赏论，甚至是一篇入门级的批评论，对初中古诗文教学具有不可替代的指导意义。

Example 1: First, the regulation problem of a simple scalar system with two subsystem is addressed. Specifically, the regulation problem can be regarded as a special case of the tracking problem with zero reference signal. The system dynamics is described as follows [30]:

Fig. 3. Evolution of the Critic NN weight elements.

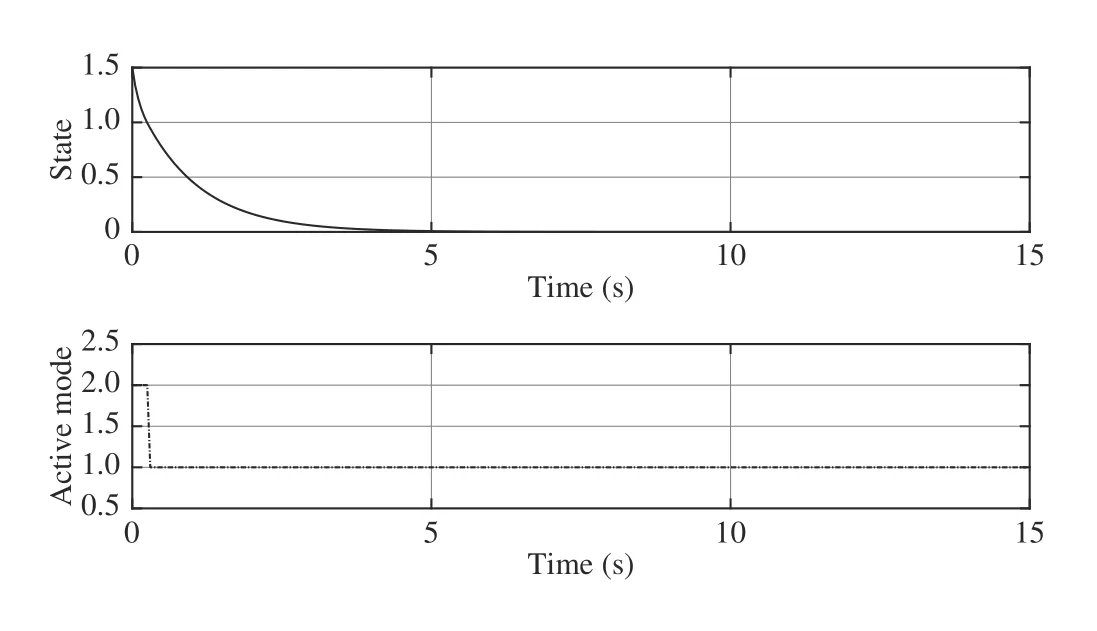
Fig. 4. State trajectory and switching mode sequence under the proposed method with x0 = 1.5.

After the training process is completed, the system is controlled by the converged policy with the initial state x0=1.5. The results are presented in Fig. 4. It is shown that the system switches to the first mode when the state becomes smaller than 1, which corresponds to (41). Moreover, let the system starts from different initial states, e.g., x0=1 and x0=−2; the results are given in Figs. 5 and 6, respectively. It is demonstrated that our method works well for different initial states.

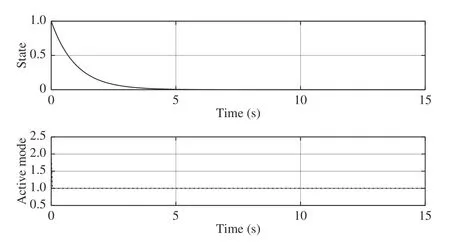
Fig. 5. State trajectory and switching mode sequence under the proposed method with x0 = 1.

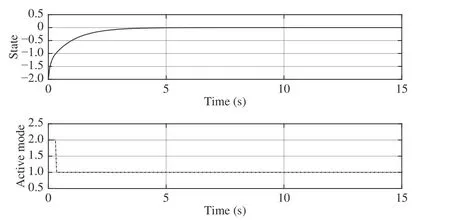
Fig. 6. State trajectory and switching mode sequence under the proposed method with x0 =－2.

Example 2: A two-tank device with three different modes is considered. There are three positions of the valve which determine the fluid flow into the upper tank: fully open, half open, and fully closed. The objective is to force the fluid level of the lower tank to track the reference signal. Let the fluid heights in the set-up be denoted by x=[x1,x2]T, where x1and x2denote the fluid levels in the upper and lower tank,respectively. The dynamics of three subsystems are given as follows [49]:

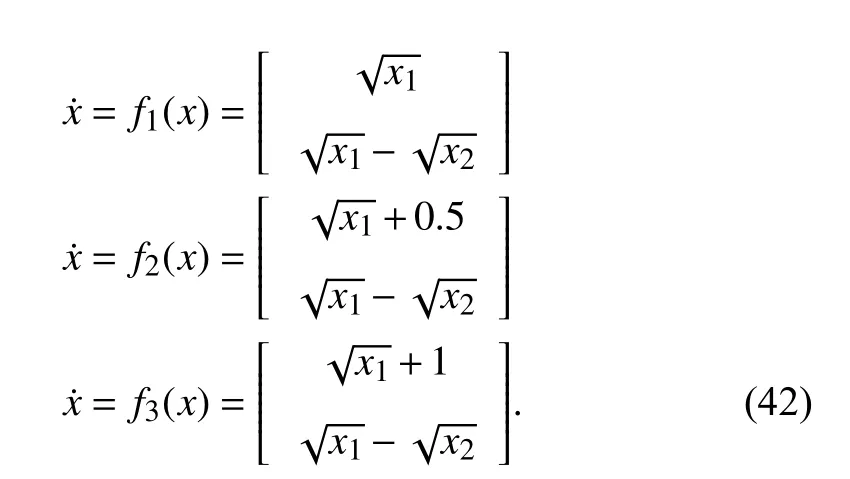
In addition, the dynamics of the reference command generator is described by

Fig. 7. Evolution of the critic NN weight elements.

Once the critic network is trained, the policy can be found by simply comparing three scalar values. Selecting the initial states as x0=[1,1]Tand s0=1, the evolution of states under obtained switching policy is shown in Fig. 8. It is shown that the fluid height in the lower tank can track the reference signal well. Furthermore, the results are compared with those of a model-based value iteration algorithm [49]. The trajectories during the interval of [200,300] are highlighted. It is shown that our algorithm achieves the same, if not better,performance without knowing the exact system dynamics. In addition, the values of performance function (3) by using the proposed Q-learning algorithm and value iteration method are 70.724 1 and 72.758 3, respectively which verifies the conclusion.

Fig. 8. State trajectories and switching mode sequence of Q-learning based x0=[1,1]T and model based method with and s0 = 1.

In order to test the tracking ability of the proposed algorithm for different time-varying reference signals, the fluid level of lower tank is forced to tracking the reference trajectories generated by , and ,respectively. Both the structure of NNs and parameters are kept the same with those in the previous paragraph. The state trajectories with different reference command generator is presented in Fig. 9 . The simulation results verify the effectiveness of our algorithm for time-varying reference trajectories.

˙s=−s2(t) ˙s=−s3(t) ˙s=−s4(t)

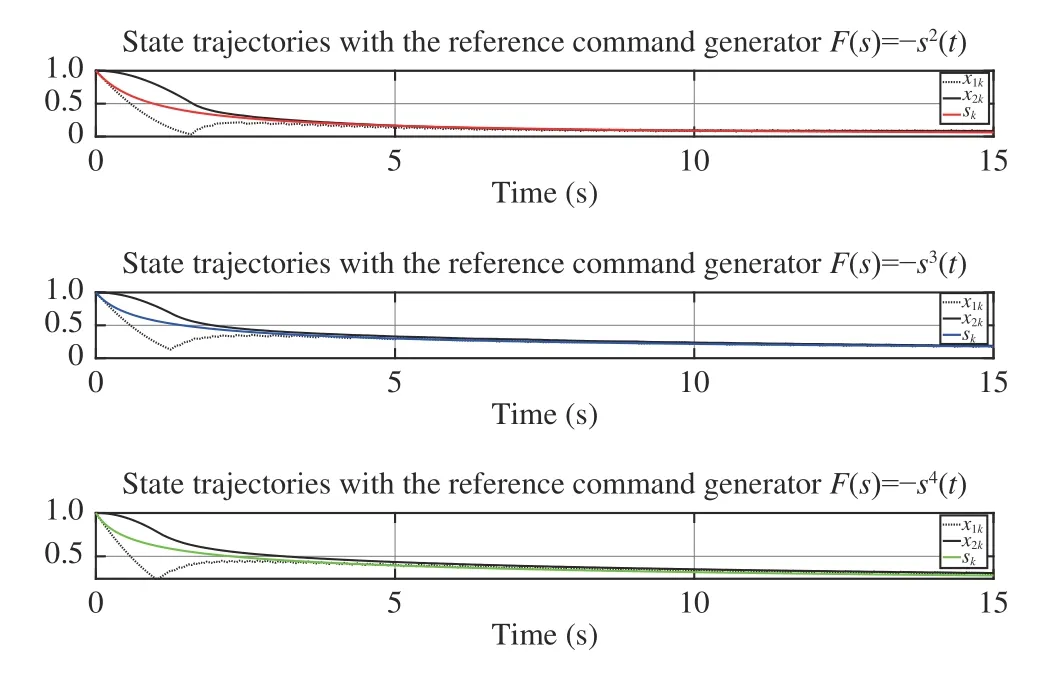
Fig. 9. State trajectories with different reference command generators.

The policy obtained after the iteration process is utilized to control the plant with the initial state x0=[0,0]T. Starting from the same state, the open-loop controller is derived according to the algorithm proposed in [12]. The trajectories of states under these two controllers are presented in Fig. 10(see top of next page). It is clear that the Q-learning controller achieves a more accurate tracking performance. By using the same Q-learning controller and nonlinear programming based controller, the simulation results with different initial state are presented in Fig. 11 (see next page). This figure illustrates the capability of the proposed method for different initial states.

Example 3: The anti-lock brake system (ABS) is considered to illustrate the potentials of the proposed algorithm for realworld applications. In order to eliminate the effect of large ranges of state variables, the non-dimensionalised ABS model is described as follows [56]:

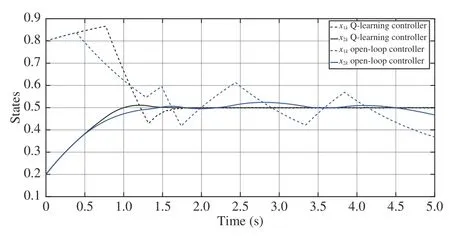
Fig. 10. State trajectories of Q-learning based and nonlinear programming based method with x0=[0.8,0.2]T and the reference signal s(t)=0.5.

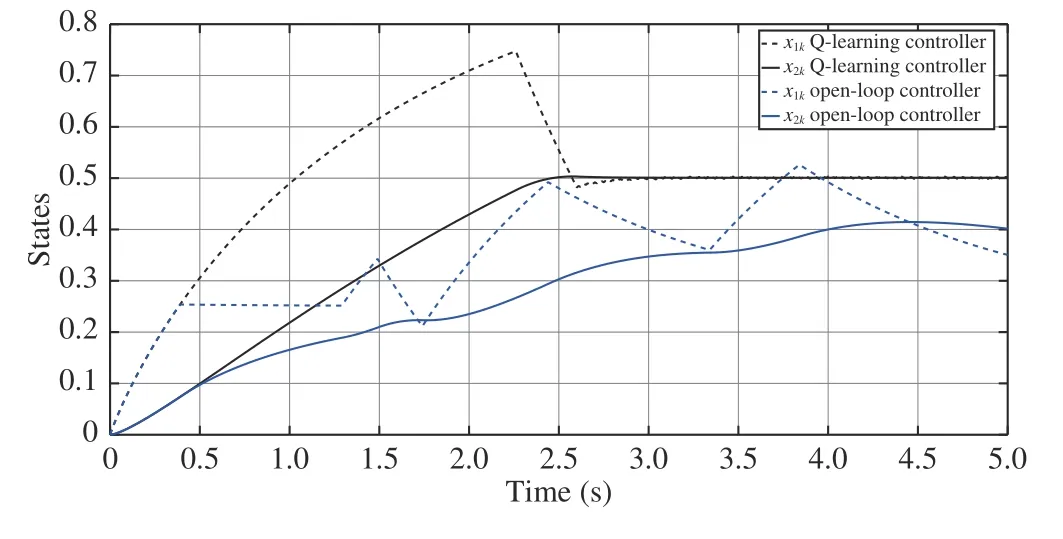
Fig. 11. State trajectories of Q-learning based and nonlinear programming based method with x0=[0,0]T and the reference signal s(t)=0.5.

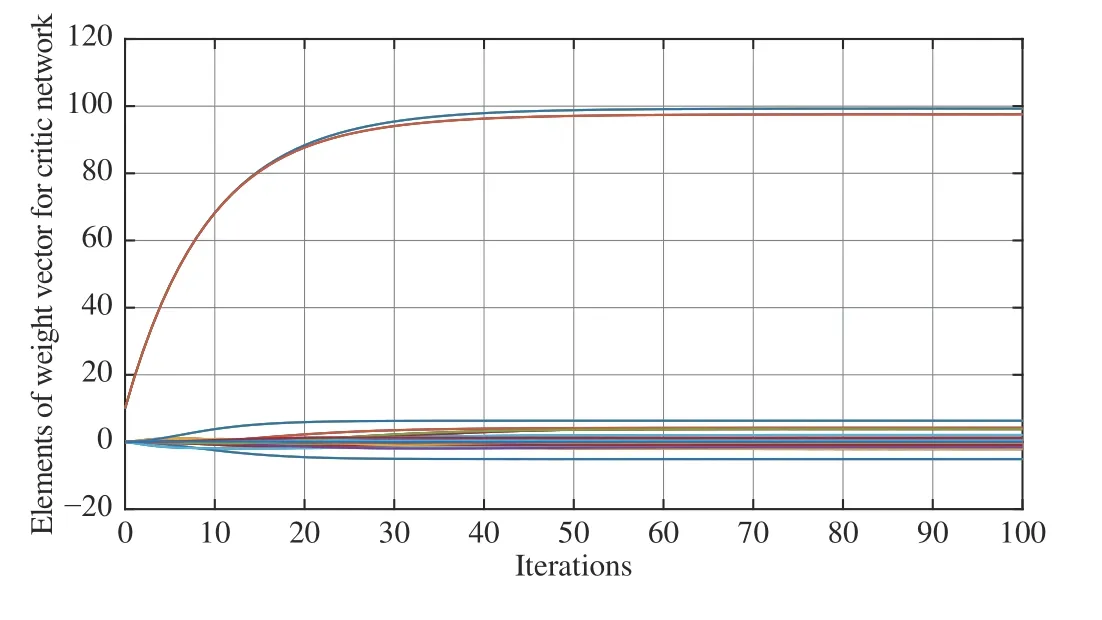
Fig. 12. Evolution of the critic NN weight elements.

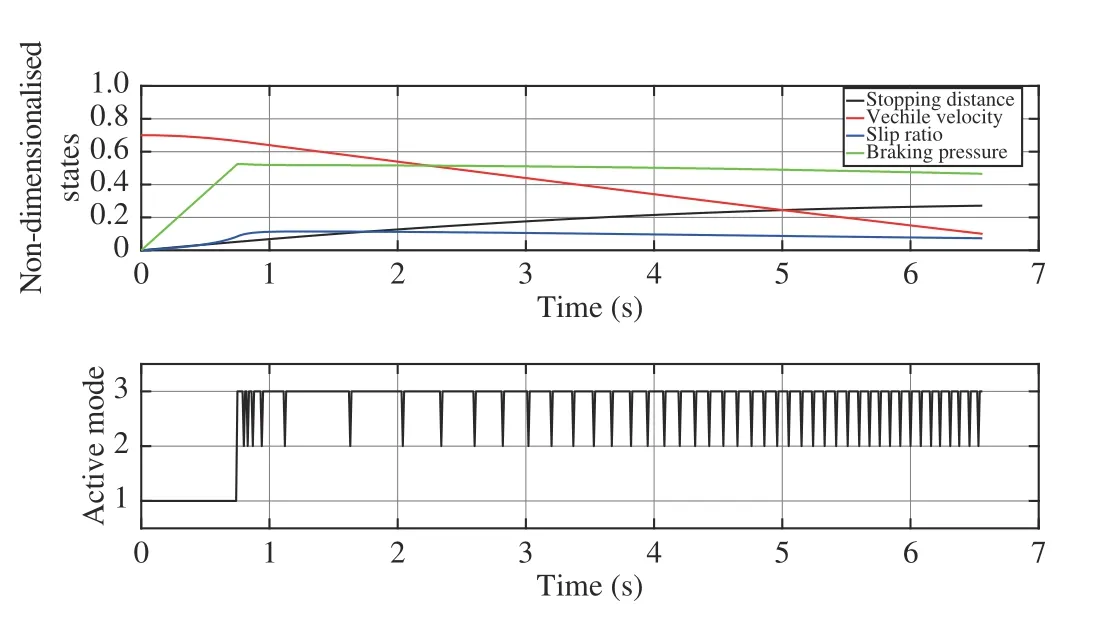
Fig. 13. State trajectories and switching mode sequence of Q-learning based method with x0=[0,0.7,0,0]T.

Furthermore, the robustness of the controller is tested with consideration of two kinds of uncertainties. First, a random noise signal with a magnitude in the range of[−0.1Ff(·),0.1Ff(·)] is added to the longitudinal force Ffin the ABS model (44). The simulation result is given in Fig. 14.The stopping distance and stopping time are 275.3 m and 6.76 s, respectively. The switching number between the three subsystems is 169 times. Compared with the case without noise, the uncertainty leads to about 0.81% increase of stopping distance, 0.75% increase of stopping time and 9 times of mode switching. Specifically, it can be seen in Fig. 14 that at the beginning of the braking process mode 2 is activated to decrease pressure. This unreasonable decision may be incurred by the random noise and leads to the degradation of performance.

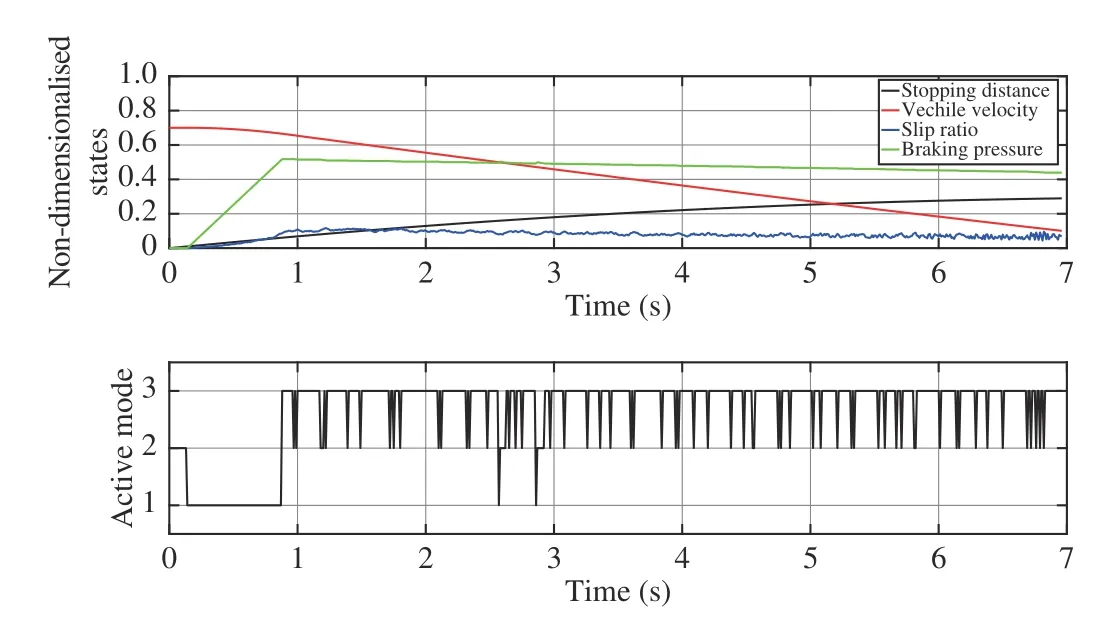
Fig. 14. State trajectories and switching mode sequence of Q-learning based method considering the uncertainty on the longitudinal force.

In addition, the uncertainty of vehicle mass is considered.During the training process, the input and output data are generated based on (44) with M=500 kg. Once the policy is trained, it is applied to control the vehicle with M=600 kg.The simulation result is presented in Fig. 15. The stopping distance and stopping time are 323.9 m and 7.96 s,respectively. The switching number between three subsystems is 125 times. It is shown that the performance is degraded compared with that without uncertainty. However, the controller has still been successful in braking the vehicle with a admissible stopping distance which demonstrates.

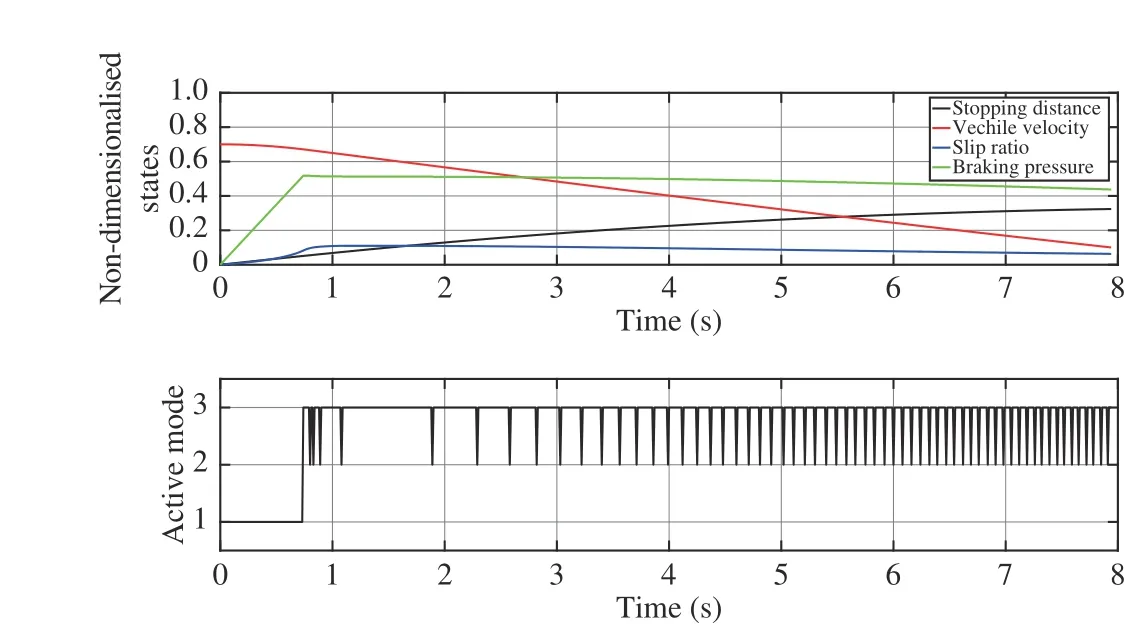
Fig. 15. State trajectories and switching mode sequence of Q-learning based method considering the uncertainty on the vehicle mass.

VI. CONCLUSIONS

In this paper, an approximated Q-learning algorithm is developed to find the optimal scheduling policy for autonomous switching systems with rigorous theoretical analysis. The learning process is totally based on the input and output data of the system and the reference command generator. The simulation results demonstrate the competitive performance of the proposed algorithm and its potential for complex nonlinear systems. Our future work is to investigate the optimal co-design of control and scheduling policies for controlled switching systems and Markov jump systems. In addition, the effect of employing deep NNs as value function approximator should be considered. It is also an interesting topic to deal with external disturbances.