数值流形法局部网格加密算法

伍书重， 莫思阳， 张友良， 张亚军

(海南大学土木建筑工程学院， 海口 570228)

数值流形法[1-2](numerical manifold method，NMM)通过有限覆盖技术，使用数值流形覆盖系统划分网格，相比有限元方法可以更加精确地计算连续及非连续物体，主要在网格划分、覆盖形式、近似函数方面有巨大优势。

使用数值流形法进行具体模型求解时，一般有两种方法可以提高计算精度。一种方法是通过使用高阶的覆盖函数来达到提高计算精度的目的。田荣等[3]开发一、二阶流形方法程序说明高阶覆盖函数提高计算精度的有效性；蔡永昌等[4-5]使用四节点四边形的数值流形覆盖系统并使用高阶覆盖位移函数提高精度；邓安福等[6]混合使用高、低阶覆盖函数，使得求解的精度和效率均得到提高；郭朝旭等[7]根据近似函数的刚度矩阵提出了LDLT算法[L指下三角单位矩阵(lower triangular identity matrix)，D指对角矩阵(diagonal matrix)，LT指L的转置矩阵(transpose matrix)]，稳定快速求得特解。高阶近似函数带来的高精度算法会出现线性相关的问题[8]。

另一种提高计算精度的方法就是网格加密。很多学者采用整体网格加密方法[9-11]，然而整体加密方法虽然提高了精度，但是却严重降低了计算效率，增加了计算时间。具体问题分析时，只有部分区域需要进行网格加密，张友良等[12]提出基于等几何分析的数值流形法，基于T样条局部加密数学覆盖网格，既提高了计算精度，又考虑了计算效率。还有一些学者借鉴有限元成熟的前处理方法进行局部网格加密[13-15]。

数值流形法使用局部网格加密以提高精度的方法稳定高效，近年来研究局部网格加密方法不是特别多。现通过对避免出现悬挂节点的加密方案进行研究并利用C++面向对象编程技术开发程序，完善了数值流形法的前处理方案，提高数值流形法的计算精度。

1 数值流形覆盖系统

数值流形方法相对于有限元方法具有的优势之一是数值流形覆盖系统，数值流形覆盖系统由三部分组成：数学覆盖(mathematical cover，MC)、物理覆盖(physical cover，PC)和流形单元(manifold elements，ME)。数学覆盖记为MCi(i=1，2，…，nMC)。物理覆盖由数学覆盖和物理网格组成，物理覆盖是数学覆盖的再剖分，由分析模型的边界线、裂缝、材料线等组成，物理覆盖记为Pij。流形元是数学覆盖和物理覆盖的交集，流形元记为eij。

数学覆盖由一个个数学网格构成，可由用户选择数学覆盖的形状以及疏密程度，但是一般根据问题需要选择规则的网格。数学网格(如图1中的3×6四边形网格)记为mi(i=1,2,…,nm)，数学网格中数学网格线的交点就是数学覆盖中心点(①～⑨)，如图2中围绕数学覆盖中心点的4个矩形构成一个数学覆盖MC。

图1 数值流形法的覆盖系统Fig.1 Cover system of numerical manifold method

图2 数学覆盖Fig.2 Mathematical cover

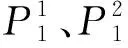
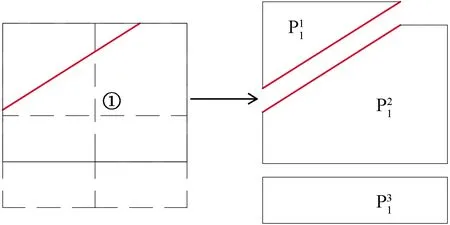
图3 数学覆盖生成物理覆盖Fig.3 Generation of physical cover from mathematical cover

图4 数学覆盖中的流形单元Fig.4 Manifold elements in a typical mathematical cover

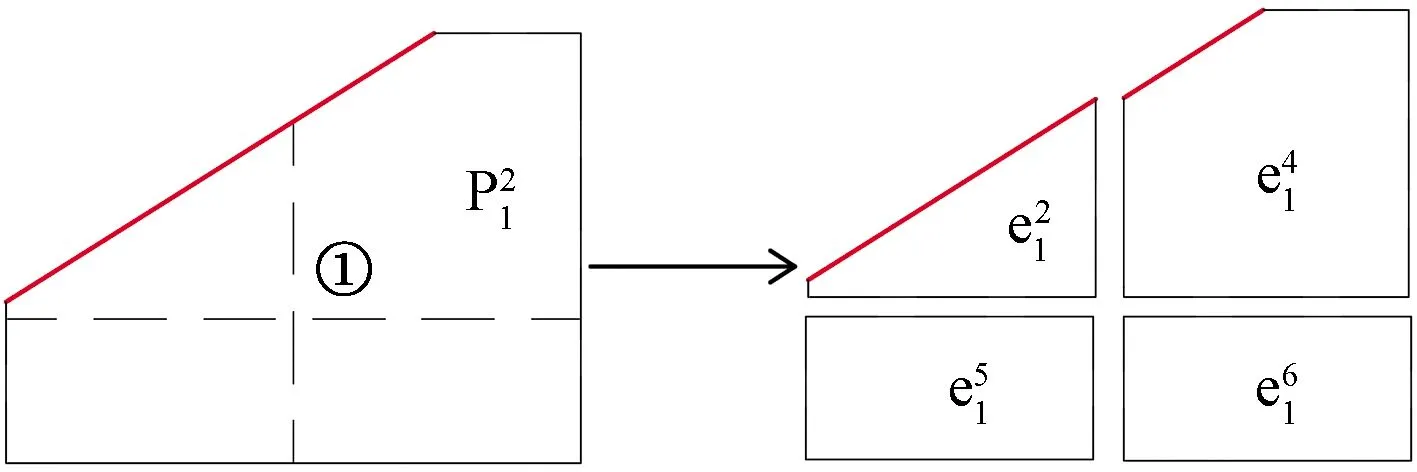
图5 物理覆盖中的流形单元Fig.5 Manifold element in physical cover

图6 一个流形单元关联的物理覆盖Fig.6 Physical Covers associated with a manifold element

以上三个概念之间的相互关系对程序设计以及进行局部加密算法非常重要。本文相关联的程序开发以Visual Studio为平台，使用C++面向对象程序设计，数学覆盖，物理覆盖以及流形元分别使用MathCover、 PhysicalCover和ManifoldElement三个类进行定义。程序设计中使用了C++STL中Map和List等数据结构，采用指针变量保存数学覆盖、物理覆盖以及流形单元。

2 局部加密方案

局部加密是计算精度与计算效率的协同。网格加密属于数值流形方法前处理，在例如裂纹尖端这样需要计算精度高处加密局部数学网格，在原有的数学网格布置完成以后，生成数值流形法覆盖系统并判断需要加密的数学网格区域，加密以后，加密区域原来生成的数学覆盖、物理覆盖以及流形单元往往会变化，需要更新以保证数值流形覆盖系统正确。局部更新数学覆盖、物理覆盖和流形元，形成新的计算单元并进行计算分析。

2.1 一到四级局部网格加密

面对不同的计算实例，不同的计算模型有不同的精度需求，本研究提出数学网格一级到四级的局部加密算法来满足不同的精度需求。该算法将数学网格加密等级分为一至四级，数学网格最终一级到四级的加密形态如图7所示。首先在裂纹尖端周围生成一个合适大小的四边形，再将四边形的4个顶点与对应数学网格的顶点连接形成一级局部加密网格如图7(a)所示；分别在顶点之间的四条连接线二等分并且将对应的二等分点连接形成二级局部加密网格如图7(b)所示；同理，分别在顶点之间的四条连接线三等分和四等分并且将对应点连接即可形成三级局部加密网格和四级加密网格，如图7(c)、图7(d)所示。

图7 数学网格局部加密示意图Fig.7 Schematic diagram of local refinement of mathematical grid

2.2 局部加密算法

对一个生成完成的数值流形覆盖系统的数学网格加密后，所产生新的网格已经不是适合分析的数值流形覆盖系统，要保证数值流形法的覆盖系统适用，必须在原有数学覆盖系统的基础上进行数学覆盖、物理覆盖以及流形元的更新，这也是本算法的难点所在。局部加密算法流程图如图8所示，该算法主要步骤如下：

图8 局部网格加密流程图Fig.8 Local grid refinement flow chart

(1)读取模型数据文件，根据计算精度需要确定加密等级。

(2)识别需要加密的区域，如裂纹尖端、应力集中区等应力梯度较大区域。

(3)根据程序预设的加密半径，若数学网格中心点至裂纹尖端的距离在加密半径内，则标记该数学网格为需被加密的网格，若数学网格中心点至裂纹尖端距离超出加密半径之外，该数学网格无需被加密。

(4)根据加密等级，需要逐一对被加密的数学网格添加加密点及加密线，对需加密区域进行加密。

(5)为防后续生成流形单元中含面积过小单元，调整距离节理线过近的数学网格点到其在节理线的垂足点上。

(6)根据加密后数学网格，依次生成加密后的数学覆盖MC、流形单元ME和物理覆盖PC。

(7)由于采用四边形进行网格划分，检查流形单元ME所对应的数学覆盖MC和物理覆盖PC数量是否均为4个，若未输出错误信息则加密完成。

2.3 裂纹尖端应力强度因子

利用已经设计好的数值流形方法程序计算裂纹尖端应力强度因子(stress intensity factor，SIF)与理论数值解进行比较是判断计算精度的有效方法。在断裂力学理论中，应力强度因子K是预测断裂发生和裂纹在带裂纹构件中扩展速率的主要标准[16]。计算应力强度因子的方法有相互作用积分法[17]、J积分法、位移外推法等。本研究采用J积分法计算应力强度因子。

与路径无关的J积分[16],可以表示为

(1)

式(1)中：Γ为按逆时针方向环绕裂纹尖端的回路曲线，曲线起点为裂纹下表面，终点为裂纹上表面；W为曲线Γ任一点处应变能密度；tx和ty为曲线Γ任一点处的应力分量；ux和uy分别为曲线Γ任一点处的位移分量；ds为沿回路曲线的弧单元。

线弹性条件下，对Ⅰ型纯张拉裂纹，J积分与KI之间存在一定的比例关系，平面应力、应变情况可以表示为

(2)

(3)

数值流形方法模拟不连续问题时出现的裂纹尖端奇异性问题，参照刘登学等[18]提出的通过将附加函数加入到覆盖函数中解决，使用这种方法，裂纹尖端可落在流形单元的任意位置。即使在相对粗糙的数学网格中，也可以精确地得到相应的应力强度因子。

3 算例验证

3.1 含有中心边裂纹的有限矩形板拉伸

如图9所示有限板[19]，侧面伸进一条长为a的边裂纹，有限板单向受拉力σ，矩形板长为2h，宽度为b，其他力学参数如表1所示。

表1 含中心边开裂纹矩形板的物理力学参数Table 1 Physical and mechanical parameters of rectangular plate with single edge crack

图9 受单向拉伸的带单边裂纹有限板Fig.9 Finite plate with single edge crack in tension

该问题的应力强度因子SIF解析解[20]为

(4)

(5)

划分网格生成的流形单元如图10所示，此时网格尚未加密，用已经编制完成的二维数值流形计算程序进行计算分析，具体计算方法可参考计算矩形板在y方向的位移uy云图并由Tecplot软件绘制[1-2]，如图11所示。在裂纹尖端分别进行一至四级局部加密，裂纹尖端加密区域如图12所示，红色虚线框内为加密区域；局部加密后求解得到的uy图如图13所示。

图10 含中心国边裂纹矩形板生成的流形单元Fig.10 Generated manifold elements in rectangular plate with sigle edge crack

图11 含中心边裂纹矩形板y方向位移云图Fig.11 uy contour plots of rectangular plate with sigle edge crack

图12 加密裂纹尖端加密区域Fig.12 Crack tip refinement area of refinement

代入具体数据后得到SIF解析解为2.877。裂纹尖端局部区域分级加密后，求解得到相应的SIF值，各级加密求得的SIF值及其与解析解的误差如表2所示。从表2中可以看出，不加密和局部加密后得到的SIF与解析解误差均不大，说明加密算法求解是有效可行的；同时，从计算结果可以看出局部加密等级越高，误差越小，得到的SIF值越精确，这也证明了此一到四级加密算法的可行性。

表2 带单边裂纹矩形板不同加密条件下的SIFTable 2 SIF of rectangular plate with single edge crack under different refinement conditions

3.2 有限板双边裂纹受单向拉伸

图14所示为一受单向拉伸的带双边裂纹有限板[19]。该矩形板底部边缘y方向位移被约束，且左下角节点位移被x、y双向约束。该算例满足平面应力条件。矩形板的各物理力学参数如表3所示。

图14 受单向拉伸的带双边裂纹有限板Fig.14 Finite plate with double edge cracks in tension

表3 带双边裂纹矩形板的物理力学参数Table 3 Physical and mechanical parameters of rectangular plate with double edge cracks

该问题的应力强度因子SIF解析解为

(6)

(7)

利用已经设置好的计算程序求解该问题，划分网格生成的流形单元如图15所示，Tecplot软件绘制出矩形板在y方向的位移如图16所示。

图15 带双边裂纹矩形板生成的流形单元Fig.15 Generated manifold elements in rectangular plate with double edge cracks

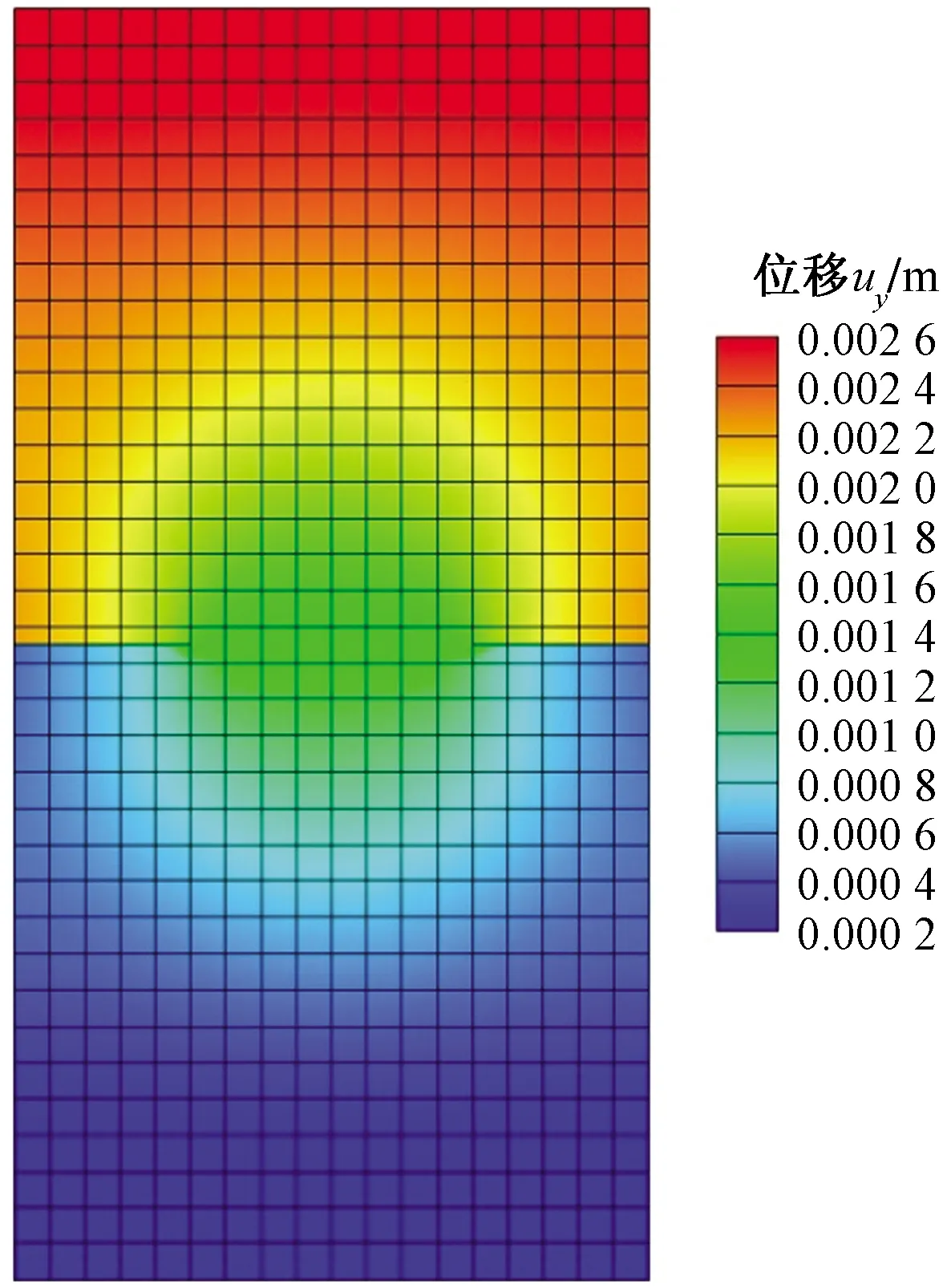
图16 带双边裂纹矩形板y方向位移云图Fig.16 uy contour plots of rectangular plate with double edge cracks

在裂纹尖端分别进行一至四级局部加密，各级加密区域及加密网格与3.1算例类似。图17所示为各级局部加密后求解得到的uy图。

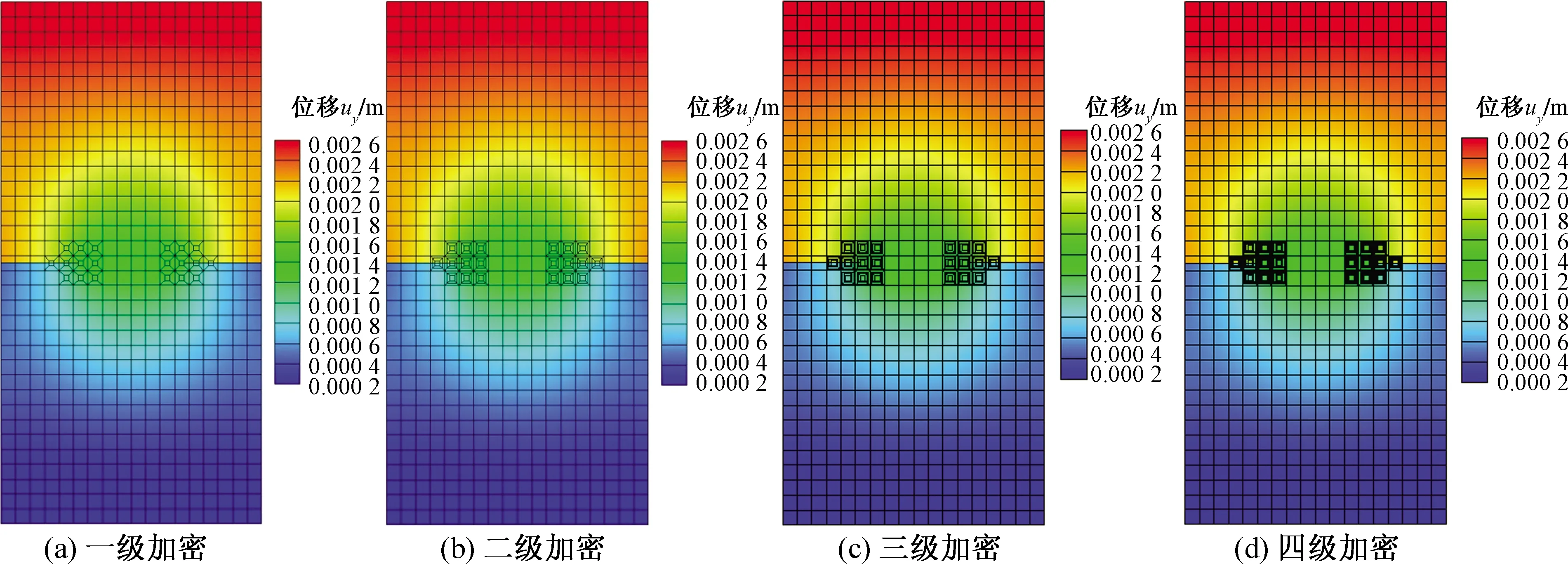
图17 加密带双边裂纹矩形板y方向位移云图Fig.17 uy contour plots of refinement rectangular plate with double edge cracks

代入具体数据后得到SIF解析解为1.199。裂纹尖端局部区域分级加密后，利用已设计好的数值流形法计算程序解得到相应的SIF值，各级加密求得的SIF值及其与解析解的误差在表3、表4中列出。从表4中可以看出，不加密和局部加密后得到的SIF与解析解误差均不大，说明利用已开发的计算程序求解是有效可行的；同时，局部加密等级越高，得到的SIF值越精确，这也证明了此加密算法的可行性。

表4 带双边裂纹矩形板不同加密条件下的SIFTable 4 SIF of rectangular plate with double edge cracks under different refinement conditions

4 结论

在非线性数值流形的基础上，考虑了模拟带裂纹结构时在裂纹尖端位移场和应力场不精确的问题，引入附加插值函数对奇异物理覆盖位移函数进行完善，并采用与路径无关的J积分方法计算应力强度因子SIF，提出了针对加密区域数学网格的加密方案予以解决。得出结论如下：

(1)对两个经典的带裂纹平板算例进行了计算分析，按照不加密、一级加密、二级加密、三级加密、四级加密的顺序对裂纹尖端需加密区域进行网格加密，程序计算得到对应的应力强度因子SIF，并列出不同加密等级下求得的SIF与解析解之间的误差，两算例存在的误差均较小，各级加密方案所得SIF误差均在5%以内。

(2)随着加密等级的提高，SIF与解析解间存在误差趋于降低，在相同半径的J积分圆轨迹条件下，第四级加密误差最小。

(3)数学网格加密方案分为一至四级，等级越高网格加密越精细。符合加密越精细，计算结果越精确的规律，说明本文算法有效。