饱和粉质黏土地基地下结构浮力折减系数

朱彦鹏, 侯喜楠, 刘润州, 马响响

(1.兰州理工大学土木工程学院， 兰州 730050； 2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心， 兰州 730050)

地下空间开发涉及诸多技术问题,其中深基础抗浮设计计算就是关键技术之一[1-2]。黏性土在中国有着广泛的分布，是一种较为常见的地基土。目前在中国对于黏性土中浮力折减系数取值问题仍没有达成共识，因此黏性土地基的浮力折减系数成为了一项重要的研究课题。崔红军等[3]认为地下水浮力不存在折减，而周朋飞[4]通过实验证明地下水存在折减，张在明[5]根据大量的室内外试验，利用渗流分析法得出地下结构浮力要比静水压力小很多的结论。李广信等[6]认为地下结构浮力应根据渗流计算确定且无论是砂土还是黏土都不能用孔隙率对其进行折减。张第轩[7]在试验模型池内分别铺填不同孔隙率的砂土和黏土，发现浮力折减系数远大于土体孔隙率，因此不能用孔隙率作为折减依据。杨瑞清等[8]针对深圳地区浮力折减情况给出了一些经验值。张乾等[9]利用简单的模型试验，针对饱和黏土地基浮力折减问题进行研究，通过试验现象初估折减系数范围为0.41～0.58，经精确计算得到折减系数为0.73。熊欢[10]利用数值分析软件与室内试验结合的方法，对地下结构底板处于粉质黏土地基和黏质粉土地基的浮力折减系数进行研究。陆启贤等[11]利用自制的模型试验装置进行了孔隙水压力传递试验和模型桶上浮试验，结果表明：孔压在黏土中传递存在滞后性且水力梯度大小会对其产生影响，最后综合两种不同的测算方法，得到黏土中折减系数取值范围为0.84～0.87。综合研究现状所述内容可知，目前对于弱透水性地基中浮力折减系数的研究尚存在以下不足：很多学者只研究了地下结构静水浮力折减系数，却忽略了渗流对折减系数的影响。在模型设计方面存在的不足，未考虑土层特性对折减系数的影响因此对于弱透水性地基中浮力折减系数的研究中，应该在考虑渗流对其影响的前提下，研制一套相对统一而合理的浮力试验装置去尝试将每种土的土层特性与浮力折减系数对应起来研究比较合理。

1 实验方案

1.1 实验思路

周明[12]设计浮力模型在考虑侧壁摩擦力时，通过摩擦因素试验测定了摩擦力系数，计算得到模型箱与土体接触的侧摩擦力。而试验中建筑模型坑体积小、模型周围土层宽度也小，这与现实中的半无限空间存在较大差异；加之土体在固结过程中，侧壁与土的摩擦性状在不断改变，使得摩擦系数也在发生变化。所以说通过计算所得的侧壁摩擦力存在明显的误差，这样的误差变化规律我们很难去测量。如何减小或者消除这些误差才是我们应该考虑的问题。

张第轩浮力模型[7]与宋林辉的模型[13]进行对比发现，其相同之处在于，虽然都把侧壁与土体摩阻力消除了，但模型箱四周直接与水接触，这样并不能准确反映工程实际情况。

张乾通过直接对比摄像头每10 min拍摄的照片来判断内箱的上浮情况[9]。这样的评判标准比较模糊，不能及时准确地反映内箱的具体上浮时间，因此用肉眼观察的方式来判定某一瞬间发生的事情是不可取的。而宋林辉[13]将土压力盒与孔隙水压力计置于模型坑内，不是用来判定内箱浮起状态的，而是测量箱底总反力及孔压的，并且由试验现象及结果可知，将二者用于试验中是可靠的。本文将借鉴这种方法，通过这两种传感器相结合的方式来判定内箱浮起瞬间，有助于提高试验结果的精确度。

针对以上浮力试验模型存在的不足，本文提出的试验模型设计思路如下：

(1)消除侧摩擦。内箱侧壁做成45°，使得侧壁土体作用在其上的土压力很小；另外，在侧壁涂一层凡士林，这样既减小侧壁摩擦系数又可以防止水从侧壁直接渗入内箱底部；当土压力和摩擦系数很小时，侧壁摩阻力也是一个更小的值。在不考虑侧摩阻力的影响下，得到比较精确的浮力折减值，从而节约工程成本，为工程实践提供理论依据。

(2)消除负压力。在内箱底部刷一层建筑砂浆以消除其与地基土接触时产生的负压力。

(3)确定箱子浮起点。试验中在结构内箱底部中心均匀埋设微型土压力盒和微型孔隙水压力计。如图1所示。从满水的箱子里每隔30 min排水12.5 kg，排水过程中土压力盒与孔隙水压力计示数不断变化，当二者测量值相等时，即为内箱浮起点。

S为土压力盒；P为孔压计图1 传感器埋设详图Fig.1 Sensor embedding details

(4)完整的渗流路径。通过将内箱各个面与地基土紧密接触来保证渗流过程中孔隙水压力传递路径的完整性。

如图2所示为试验装置的概化模型，当消除内箱侧壁与土体之间摩擦力后，内箱共受到四种力作用，建立平衡关系式为

图2 实验系统概化模型Fig.2 Generalized model of experimental system

Ww+W箱=F土+F′浮

(1)

式(1)中：W箱为内箱自身重量；W水为内箱水的重量；F″浮为内箱在饱和土中的浮力；F土为土骨架承担的力。

内箱浮起瞬间所受浮力实际值的确定办法有两种：①在内箱底部只埋设孔隙水压力计，孔隙水压力计实测值可以反映浮力值大小，但是这种方法无法确定内箱浮起瞬间；②在内箱底部同时埋设土压力盒和孔隙水压力计，当土压力盒测量值等于孔隙水压力计时，内箱刚好浮起，此时浮力等于内箱与箱内水重力之和。显然，第二种方法可以科学合理地确定内箱起浮瞬间，本文即采用这种方法来确定浮力实际值。

通常把折减系数表示为地下结构在饱和土中浮力实测值与在纯水中浮力计算值的比值。折减系数的大小直接反映建筑物在地基土中浮起的难易程度，折减系数越大，则说明建筑物所受实际浮力越接近理论值，越容易受地下水影响。其中，折减系数η的计算公式为

(2)

式(2)中：F浮为内箱浮起瞬间所受浮力实际值，kN;F浮理为内箱在纯水中受到的浮力,kN。

由于内箱从未浮到浮起瞬间始终在饱和地基中，V排始终不变，由阿基米德公式F浮理=ρ液gV排可知，当内箱刚开始浮起时，内箱所受到理论浮力即为排开内箱体积的这部分水的重力，因此本试验F浮理为一定值，即V排=0.456 m3，F浮理=ρ液gV排=1 000 kg/m3×10 N/kg×0.546 m3=4.56 kN。

试验系统主要包括被测单一土质，3 mm厚的六面锥体铁箱，3 mm厚的中心内空凹槽六面体铁箱等三个部分。孔隙水压力计和土压力盒分设在0.5 m土层上部且位于六面锥体底部中心，目的是判定锥形箱的上浮瞬间。

1.2 实验模型

试验模型包括模型坑(外箱)和模型箱(内箱)。其中，外箱如图3所示，尺寸为1.8 m×1.8 m×1.5 m，箱体由厚5 mm的铁皮采用双面焊缝焊成，确保模型坑密封和变形；在其内部填铺单一土质来模拟地基。内箱侧壁与水平地面呈45°的倒梯形台代表地下结构如图4所示，箱体用厚3 mm铁皮制成，箱体高0.6 m，质量64.2 kg；上底面开口，尺寸为1.4 m×1.4 m，下底面封闭，尺寸为0.2 m×0.2 m。其他设备还有微型土压力盒、孔隙水压力计、电脑、XL2101C程控静态电阻应变仪、注水工具等。

图3 实验模型图Fig.3 Experimental model diagram

图4 实验模型箱Fig.4 Experimental model box

粉质黏土地基土的结构状态参数共测量了4次，具体结果如表1所示。

表1 粉质黏土地基结构状态参数测量结果Table 1 Measurement results of structural parameters of silty clay foundation

1.3 实验步骤

实验采取减重上浮思路，即不断排出内箱中的水，箱中水位下降，同时底部总压力与孔隙水压力也发生变化；当总压力实测值与实测值相等时，可判定此时为内箱上浮的临界状态。

1.4 数据处理

结合微型土压力盒与孔隙水压力计测试结果，确定内箱浮起时刻，得到浮力实际值并与理论值进行比较，计算折减系数。

本次实验数据是在土体结构状态参数为干密度ρd=1.55 kg/m3、孔隙率n=0.372、渗透系数K=7.60×10-6cm/s的地基中采集的。实验结束后，分别绘制内箱水位高度与箱底土压力盒和孔隙水压力计测量结果之间的关系曲线，如图5、图6所示。

图5 土压力盒实测曲线Fig.5 Earth pressure cell measured curve

图6 孔隙水压力实测值Fig.6 Measured value of pore water pressure

1.4.1 土压力盒测量结果分析

由图5土压力盒实测曲线可知，埋入该地基土中的6个土压力盒所测压力值变化趋势基本一致,均呈指数函数形式变化，实测值和拟合值较吻合。

1.4.2 孔隙水压力计测量结果分析

由图6可知，埋置于内箱底部的两个孔隙水压力计实测曲线均呈不同程度的下降趋势，拟合度较高。随着内箱中水的不断排出，曲线斜率逐渐变小，直到箱底的孔隙水压力刚好能把内箱浮起。

对比土压力盒实测曲线(图5)和孔隙水压力计实测曲线(图6)发现，当排水到第14、15次时，内箱底部土压力盒实测值压力与孔隙水压力相等，说明内箱开始上浮，此时的水位高度为0.4871～0.496 0 m，其实测浮力通过计算得该值范围为2 685～2 810 N，浮力理论值为4 560 N，折减系数的变化范围为0.730 0～0.757 0。最终取平均值0.744 0作为本次试验浮力折减系数值。本次试验结果可为以后黏性土地基中浮力折减系数的研究提供参考。

2 数值模拟

2.1 模型建立

将利用COMSOL Multiphysics对室内模型所受浮力进行仿真分析并结合室内试验验证模拟的可靠性，然后拓展不同的试验工况，三维几何模型尺寸为1.8 m(长)×1.8 m(宽)×1.1 m(高)，如图7所示。

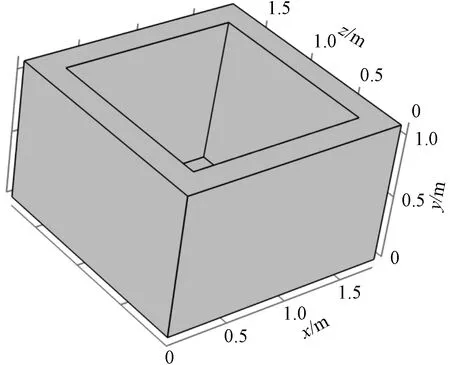
图7 三维几何模型Fig.7 3D geometric model

为了模拟试验的排水过程，定义插值函数int(t)来表示水头高度与时间t之间的关系，以地面作为绝对压强计算基准面，每半小时排出等质量的水，其水头变化如图8表示。

图8 水头高度位随时间变化的插值函数Fig.8 Interpolation function of height change with time

图9所示为达西边界设置情况，打开重力节点，边界1、3、4、5、7、8为不透水边界，边界2、6为p=0边界；图10所示为固体力学边界设置情况，边界1、3、4、5、7为辊轴约束，边界2、6为自由边界，边界8为固定约束。

图9 达西边界条件设置Fig.9 Darcy boundary condition setting

图10 固体力学边界设置Fig.10 Solid mechanics boundary settings

2.2 模拟结果分析

对粉质黏土浮力进行数值模拟，结果显示：内箱底部中心土体有效应力值随内箱水位高度变化曲线如图11所示，由该曲线可知，内箱底部中心土体有效应力值为0时，当内箱上浮，箱中水位高度为0.495 0 m，此时土体有效应力云图如图12所示。当内箱水位高度为0.495 0 m时其所受实际浮力为3 438.2 N，浮力理论值为4 560 N，经计算得折减系数为0.754 0。内箱底部中心处孔隙水压力值随内箱水位高度变化曲线如图13所示，此时孔隙水压力分布云图如图14所示。

图11 内箱底部中心有效应力曲线Fig.11 Effective stress curve at the bottom center of the inner box

图12 内箱底部中心有效应力云图Fig.12 Effective stress cloud at the bottom center of the inner box

图13 内箱底部中心孔隙水压力曲线Fig.13 Water pressure curve at the center of the bottom of the inner box

图14 内箱底部中心孔隙水压力云图Fig.14 Cloud pressure cloud at the bottom of the inner box

将模拟值与室内试验实测值进行对比，发现模拟的总压力值与室内试验实测值符合较好且孔隙水压力变化趋势基本一致。此外，室内试验所得折减系数值为0.744，本次模拟分析所得折减系数为0.754 0，模拟值与实测值基本吻合。所以取该结构状态下浮力折减系数为0.754 0。

为后面进行多元线性回归分析，又模拟了其他的工况，结果如表2所示。

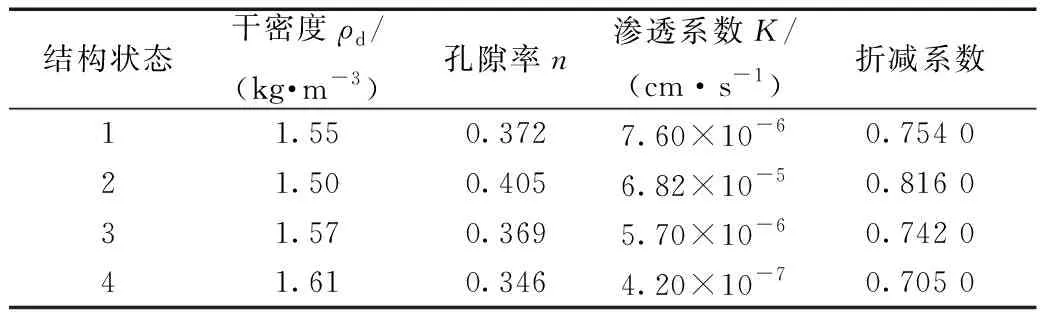
表2 粉质黏土结构状态及折减系数Table 2 Silty clay structure state and reduction coefficient

3 多元线性回归分析

在统计学中常用的一种拟合方法是多元线性回归法，该方法主要用于分析一个因变量受多个自变量共同影响的问题[14]。为了确定浮力折减系数的定量预测模型，本文尝试初步建立三元线性回归模型，在此模型基础上不断排除共线性变量，最终得到拟合度较高的一元线性回归模型，可用于以后折减系数的预测。回归方程拟合中折减系数η，是衡量建筑物所处不同饱和地基中所受浮力大小的重要指标，且可能会与干密度ρd、孔隙率n和渗透系数K这三个因素有关。

通过对表的参数及折减系数的计算，可得到η与ρd、n、K之间的线性相关性。综合得到的结果见表3。

表3 初次检验η与ρd、n、K间的R、P和显著性Table 3 Initial test of R value, P value and significance between η and ρd, n, K

由表3可得，η与ρd、n、K之间的线性相关性都显著。由此可以尝试建立三元线性回归方程。

利用数据分析软件SPSS进行多元线性回归拟合，运行后所得结果如表4所示。初步建立的三元回归方程为

表4 三元线性回归的参数估计Table 4 Parameter estimation of ternary linear regression

η=-0.466ρd+0.744n+233.079K+1.198

(3)

对式(4)所建方程进行显著性检验，原假设H0与备择假设H1为

(4)

假如检验所得P<0.05，则原假设不成立，所得方程整体上显著。回归方程整体性检验结果如表5所示。

表5 三元线性回归方程整体显著性检验结果Table 5 Test result of overall significance of ternary linear regression equation

由表5可知，初次建立的三元回归方程整体上是显著的。但这并不能说明方程中的每个自变量都显著，因此要对自变量进行共线性诊断。

4 多重共线性诊断

如果初步建立的线性回归方程中包括两个或者两个以上自变量且多个自变量之间线性相关性很高，则说明本次所建立的方程可能是失败的且对该方程的所有分析也是无效的，我们把这种现象称作多重共线性问题。因此为了得到较为理想的方程，有必要对初步建立的多元线性方程进行多重共线性诊断。

通过自变量的方差膨胀因子VIF值具体所在区间来诊断。第i个自变量关于其他自变量的方差膨胀因子VIFi的计算方法为

(5)

表6中，当VIF>10，自变量之间共线性严重，为了使拟合关系准确合理，必须采用去除某些变量、变量之间变换、主成分分析以及岭回归等方法来消除变量共线性。

表6 多重共线性诊断规则Table 6 Multicollinearity diagnosis rule

用SPSS计算各自变量所对应的VIF值如表7所示。

表7 三元回归的方差膨胀因子Table 7 Variance inflation factor for ternary regression

由表7可发现ρd与n这两个自变量的VIF>10，所以要剔除这两个自变量，保留自变量K。重新拟合方程，最终得到的一元线性回归模型[式(6)]，拟合所得R2=0.867，拟合度很好，具有很高的参考价值。

η=1 344.3K+0.726 7

(6)

5 结论

(1)通过实验得到粉质黏土在结构状态参数为干密度ρd=1.55 kg/m3、孔隙率n=0.372、渗透系数K=7.60×10-6cm/s情况下，所得浮力折减系为0.744 0，这可为以后实际工程抗浮设计中遇到类似情况提供理论依据。

(2)运用多元线性回归初步建立土体孔隙率、干密度、渗透系数与浮力折减系数的关系，得出粉质黏土为η=-0.466ρd+0.744n+233.079K+1.198，对方程中变量进行共线性诊断，最终确定粉质黏土折减系数与渗透系数关系：η=1 344.3K+0.726 7，方程拟合优度R2均大于0.71，可为日后浮力折减系数取值提供参考。