不确定性条件下储能配置辅助决策方法

司学振, 李朝晖, 杨海晶, 饶宇飞, 施 涛

(1.国网河南省电力公司电力科学研究院， 郑州 450052； 2.南京邮电大学先进技术研究院， 南京 210023)

近年来，随着风电、光伏发电等新能源发电技术的大规模推广和应用，新能源装机容量占电力系统总装机容量的比例也不断增长[1-2]。截至2018年底，中国风电装机容量达1.8亿kW，太阳能发电装机容量达1.7亿kW[3-4]。由于新能源发电受风速、光照等自然资源条件的影响，其出力呈间歇性、随机性和波动性。新能源发电装机容量大规模增长的同时，对电力系统的灵活调节需求也不断增长[5-6]。为提高系统的灵活调节能力，促进新能源的消纳，除兴建大型抽水蓄能电站外，以电池为代表的新型电力储能技术也在用户侧、场站侧得到了广泛的应用[7]。而在电网侧，目前在河南、江苏等地相继开展了电网侧储能电站的建设和示范运行，旨在通过合理布局和优化配置，充分挖掘和利用多点分散式储能电站的聚合效应，进而满足不同场景下电网的灵活调节需求[8-9]。关于储能的优化配置问题，目前主要集中于用户侧、场站侧等独立应用场景下储能配置问题的研究，对电网侧储能的配置问题研究较少。其中，王典等[10]针对并网型光储微电网，以平准化度电成本最小化为目标，建立了电源容量优化配置模型。陈旭海等[11]采用经济性评估法构建了储能系统的经济运行模型，并用于储能配置辅助决策分析中。贾雨龙等[12]提出了一种分布式储能系统接入配电网的容量配置和有序布点的双层模型。杨锡运等[13]提出一种基于商业园区源/储/荷协同运行的储能系统多目 标优化配置模型。赵冬梅等[14]构建了包含电转气装置的热电联产微网电/热综合储能优化配置模型。

现主要针对新能源消纳中的储能配置问题，基于随机规划理论，建立一种考虑需求场景不确定性的储能电源配置期望值模型，提出基于场景聚类和遗传算法相结合的求解步骤与方法，并在含风电场的某典型区域电力系统上进行算例分析，验证方法的可行性和有效性。

1 基于期望值模型的随机决策原理

含有随机变量的数学规划问题属于随机规划问题。其中，使目标函数的期望值最优化的决策模型称为期望值模型，其一般数学表达式[15]为

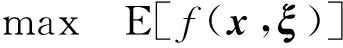
(1)

(2)

式中：x为n维决策向量；ξ为t维随机向量，其概率密度函数为Φ(ξ)；f(x,ξ)为目标函数；gj(x,ξ)和hk(x,ξ)为随机约束函数；E为期望值算子。设Rt为t维空间域，从而有

(3)

(4)

(5)

若ξ为离散型随机向量且分布函数Pr(ξ=ξi)=θi(i∈I，其中I为序号集)，则有

(6)

(7)

(8)

设可行解x*是期望值模型的最优解，对任意的可行解x，E[f(x*,ξ)]≥E[f(x,ξ)] 成立。

2 含储能的新能源并网消纳生产模拟

本节建立包含储能设施的新能源并网消纳生产模拟模型，可根据生产模拟计算结果评估当前储能配置方案下新能源消纳水平。

2.1 目标函数

以新能源实际发电量最大化为目标，建立新能源并网消纳生产模拟模型，数学表达式为

(9)

式(9)中：N为时间周期包含的时段数目；M为新能源场站数目；Pij为第j个新能源场站在第i个时段的实际出力；Δt为单位时段的时长。

2.2 约束条件

新能源并网消纳生产模拟考虑的约束条件主要包括：功率平衡约束、机组出力约束、爬坡约束、旋转备用约束、储能电池充放电约束等。

(1)功率平衡约束

(10)

式(10)中：G为常规机组数目；Pik为第k台常规机组在第i时段的实际出力；PiD为第i时段的系统负荷；PiL为第i时段的系统网损。

(2)常规机组出力约束

Pk,min≤Pik≤Pk,max

(11)

式(11)中：Pk,max为第k台常规机组出力上限；Pk,min为第k台常规机组出力下限。

(3)调节电源爬坡约束

-Rk,-tmax≤Pik-P(i-1),k≤Rk,+tmax

(12)

式(12)中：tmax为最大允许爬坡时间；Rk,-为第k台调节电源向下调节速率；Rk,+为第k台调节电源向上调节速率。

(4)旋转备用约束

(13)

(14)

式中：PiR,+为系统在第i时段向上旋转备用要求；PiR,-为系统在第i时段向下旋转备用要求。

(5)储能设施充放电约束

Pe,min≤|Pie|≤Pe,max

(15)

(16)

SOCmin≤SOC≤SOCmax

(17)

式中：Pe,min为储能设施充放电功率下限；Pe,max为储能设施充放电功率上限；Pie为储能设施在第i时段充放电功率；放电为正、充电为负；Ei为储能设施当前的能量状态；Erate为储能设施的额定能量状态；SOCmin、SOCmax为储能设施充放电深度上下限。

3 基于生产模拟的储能配置辅助决策流程

基于生产模拟的储能配置辅助决策流程如图1所示。由于新能源并网消纳生产模拟中需要基于大量的历史数据，建立具有典型意义的时序场景，这些场景涵盖年、月、日等不同的时间尺度。对于时间跨度较长的场景，为了提高计算效率，通常采用聚类分析的方法，对场景进行聚类和缩减，建立新能源并网消纳典型场景集，记为S，该场景集包含从s1到sm共m种典型场景。图1中，设i为典型场景编号，则i=1,2,…,m，如式(18)所示。典型的聚类方法有K-Means、K-Medoids算法等。

图1 储能配置辅助决策流程Fig.1 Auxiliary decision-making of ES configuration

S=[s1s1…sm]

(18)

设ηmax为新能源消纳目标指标要求，即弃风/弃光率η<ηmax。基于生产模拟模型，采用遗传算法求取每个典型场景下的满足新能源消纳目标所需的储能容量和能量参考值Ps,ref和Es,ref。

根据各类典型场景的随机概率和每个场景下通过生产模拟获得的配置方案参考值，计算储能配置方案的数学期望EX，即

(19)

(20)

在实际工程应用中，储能配置除需满足场景需求外，还考虑一定的备用和可靠性要求。因此，最终储能配置方案选取应满足：

P′ref=Prefcp,cp>1

(21)

E′ref=Erefce,ce>1

(22)

式中:cp、ce为修正系数，视实际工程应用要求而定。

4 案例分析

以某区域电力系统为例，通过生产模拟分析其在不同场景下的风电消纳情况，并根据弃风率要求，计算所需的储能配置方案，验证上述方法的有效性。系统的基准容量100 MV·A；系统旋转备用系数要求为5%；弃风率要求低于5%；网损占系统负荷的3%。各常规机组参数如表1所示。

表1 电源类型与参数Table 1 Types and parameter of generation units

根据当地风力发电和负荷需求历史数据，通过场景聚类，建立典型日风电出力和负荷需求场景集。本文选取最有代表性的10种典型日场景进行分析，如表2、表3所示。

表2 典型日风电出力特性(标幺值)Table 2 Wind power output characteristics under typical scenarios (pu)

表3 典型日负荷特性(标幺值)Table 3 Load characteristics under typical scenarios (pu)

则基于上述各典型日场景下的风电出力与负荷特性，按照图1中决策流程，基于生产模拟模型对每个典型场景下的储能配置需求进行求解。以场景2为例，通过生产模拟计算可知其在储能配置前弃风率为7.32%，为满足弃风率低于5%的要求，利用遗传算法迭代求解，可得场景2下的储能容量/能量配置需求为5 MW/26 MW·h。则储能配置前后风电功率的消纳情况如图2所示。

由图2可知，场景2中风电消纳的瓶颈时段主要在00:00～05:00。此时，夜间负荷处于低谷，消纳空间有限。在配置储能后，弃风率由初始的7.32%下降至3.90%，满足弃风率低于5%的要求。基于生产模拟模型，逐个依次求得每个典型场景下的储能配置需求，如表4所示。

表4 不同场景下的储能配置需求Table 4 ES requirements in different scenarios

图2 场景2下的风电消纳特性Fig.2 Wind power accommodation characteristic in scenario 2

在实际工程中，储能配置还需要在考虑一定的备用要求、可靠性要求以及储能模块额定值等因素，对储能配置方案予以修正。本案例中为修正系数取cp=1.1，取ce=1.05，则最终的储能配置需求推荐方案为7 MW/42 MW·h。

5 结论

针对新能源消纳中的灵活调节需求的不确定性，基于随机规划理论，建立了基于新能源并网消纳生产模拟的储能电源配置期望值辅助决策模型，提出了基于场景聚类和遗传算法相结合的模型求解算法步骤，并在基于某典型区域电力系统进行算例分析，验证方法的可行性和有效性。基于期望值模型的储能配置辅助决策方法能够较好地量化新能源功率波动带来的需求场景不确定性，实现目标期望值的最优化，对提高储能配置的量化决策水平，促进新能源消纳具有积极作用。下一步将从辅助服务市场的角度，深入研究新能源消纳需求下的储能配置成本效益量化模型和辅助服务定价机制，从技术性和经济性两方面考虑储能技术在电力系统的配置和应用。