基于灰关联分析的加筋土挡墙频率敏感因子

李 倩, 张瑞刚, 凌天清

(1.重庆交通大学土木工程学院， 重庆 400000； 2.重庆交通大学水利水运工程教育部重点实验室， 重庆 400041； 3.水利部长江水利委员会河湖保护与建设运行安全中心， 武汉 430010)

加筋土挡墙为柔性支挡结构，具有良好的抗震性能，大量用于新建工程及加固路堤等基础设施建设中[1]。加筋土挡墙主要是利用拉筋与土之间的摩擦作用，改善土体的变形条件和提高土体的工程特性，具有自身轻便、协调变形能力强的特点[2]。

由于加筋土本构关系的复杂多变，中外研究者对加筋挡土墙的强度和变形问题以试验方法、数值分析研究为主。杨果林等[3]通过加筋土挡墙动力特性模型试验研究了加筋土的动力失稳、动变形、动强度和动应力-应变关系；程亚男等[4]运用拟动力法和水平条分法研究了不同筋材条件下加筋土挡墙地震稳定性；汪承志等[5]通过对某直立式格栅加筋挡墙进行现场测试，分析了加筋材料不同部位应力分布。也有学者运用数值模拟方法进行加筋挡土墙的研究,如:肖雁征等[6]以具体工程为例，运用有限元数值计算，对加筋土挡土墙稳定性进行研究；周凤玺等[7]结合了室内模型试验与数值模拟方法，对条带式加筋土挡墙的作用机理进行研究；程火焰等[8]通过非线性有限元法与试验方法分析了地震动力对加筋材料与土体间的动似摩擦系数的影响；Ghanbari等[9]研究了面板与填土相互作用的挡墙面板振动频率计算，采用瑞利法求解面板振动频率；Ramezani等[10]将面板分为刚性转动与弯曲转动计算了面板振动频率；Abbasi等[11]将面板振动频率考虑为筋材受拉力与筋材不受力的情况进行求解。这些研究对加筋土挡墙的振动特性进行了有益探索，但却无法揭示不同填土体参数之间关联性对挡墙振动特性的影响。

采用ABAQUS建立加筋挡土墙有限元模型,并对挡墙振动前3阶模态及振动频率进行分析。引入灰关联分析法，以弹性模量、泊松比、重度等5个参数为影响因素，分析其与振动频率之间的关联度，揭示加筋挡土墙振动特性敏感因子。并进一步研究了主要敏感因子与振动频率之间的变化规律，为加筋挡土墙的设计和研究提供理论参考。

1 加筋挡土墙有限元模型

1.1 频率求解方程

由动力学理论，系统的运动平衡方程为

(1)

令C=0、F=0，便得到结构的无阻尼自由振动方程为

(2)

式(2)为二阶常系数齐次常微分方程，其解的形式为

δ(t)=φsin(ωt)

(3)

式(3)中：ω为结构自由振动频率；φ为体系的形状(它不随时间而变，只是振幅变化)，将式(3)代入式(2)，可得

(K-ω2M)φ=0

(4)

式(4)为线性其次方程组，若要有非零解，其系数矩阵行列式必须为零，即

|K-ω2M|=0

(5)

式(5)称为常微分方程组的特征方程，它的解ω称为结构的频率，具有最低频率的振型叫做第一振型，第二低频率的振型叫做第二振型。

由频率方程可知，结构体系的振动特性只与结构的刚度、质量有关，而与外部作用荷载无关，所以它反应的是结构体系固有特性，研究结构体系的振动频率便可知结构体系的固有抗震性能。

1.2 几何模型与参数

以重庆某加筋土挡墙为例，墙高10 m，长25 m，基础深度1 m，筋带长度10 m，垂直间距50 cm。挡墙模型主要材料参数包括：填土弹性模量E、泊松比υ、重度γ、黏聚力c、内摩擦角φ。使用有限元软件ABAQUS建立加筋土挡墙频率计算模型。有限元模型高10 m，墙后填土宽度为20 m，每0.5 m设置一层筋材，筋材长度为10 m。有限元模型如图1所示，模型计算参数如表1所示。

表1 加筋挡土墙模型参数Table 1 Model parameters of reinforced retaining wall

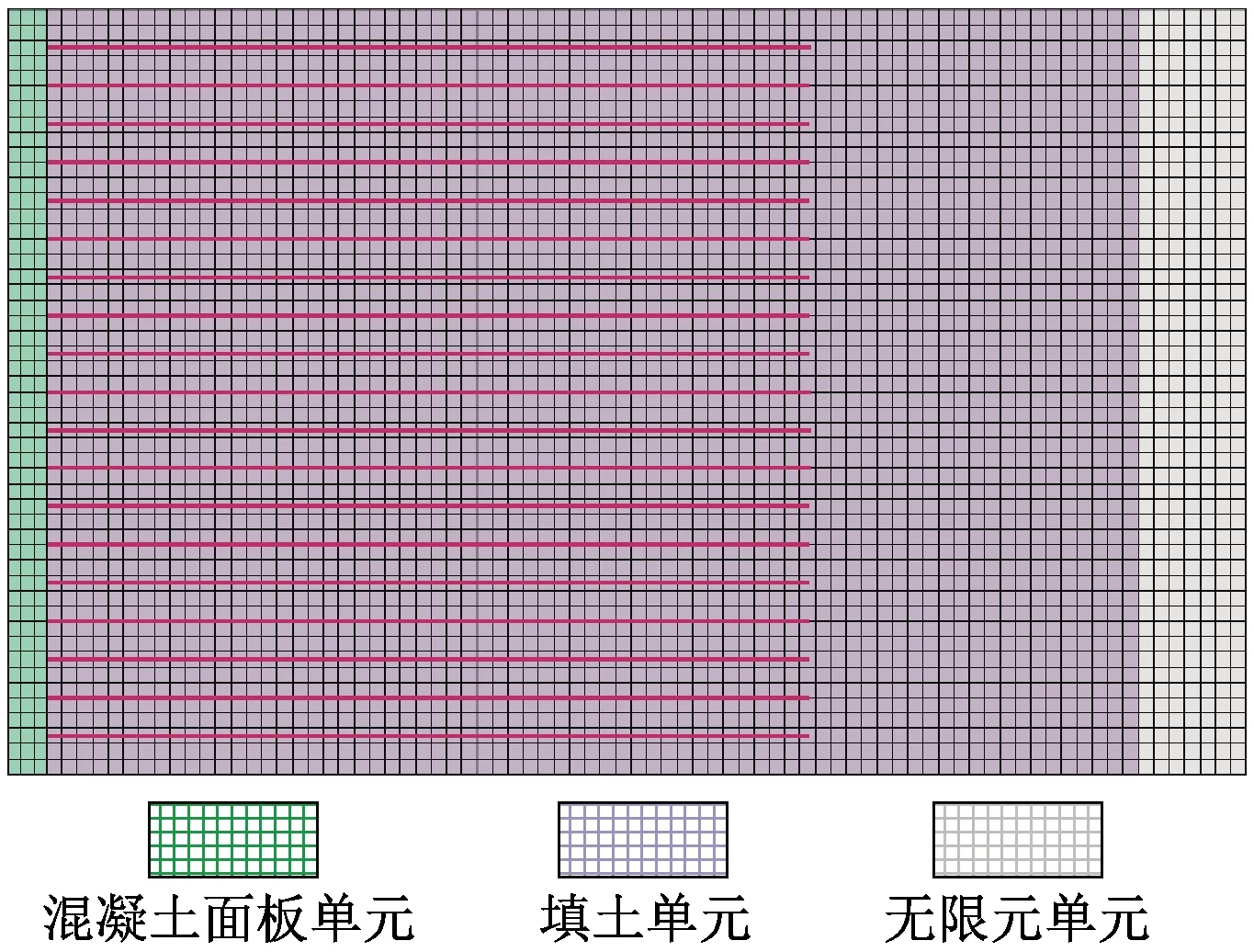
图1 频率计算有限元模型Fig.1 Finite element model for frequency calculation

有限元模型采用CINPE4平面应变无限单元模拟墙后填土的无限边界条件。挡土墙面板与墙后填土之间设置接触行为，接触属性采用小滑动跟踪方法的面对面接触形式，切向接触行为采用惩罚函数算法，法向接触行为采用硬接触形式。

加筋材料与填土之间的约束采用Embedded region约束类型，Embedded region约束功能可以在主体单元中嵌入加筋材料，并保证节点具有主体单元相应位置处的位移自由度，能够合理地模拟土工格栅、钢筋等加筋材料。

2 振动特性分析

保持地基土与混凝土挡墙的参数不变，改变挡墙后边坡土的弹性模量和泊松比，分别计算工况一至工况五条件下结构体系的前三阶频率，如表2所示。

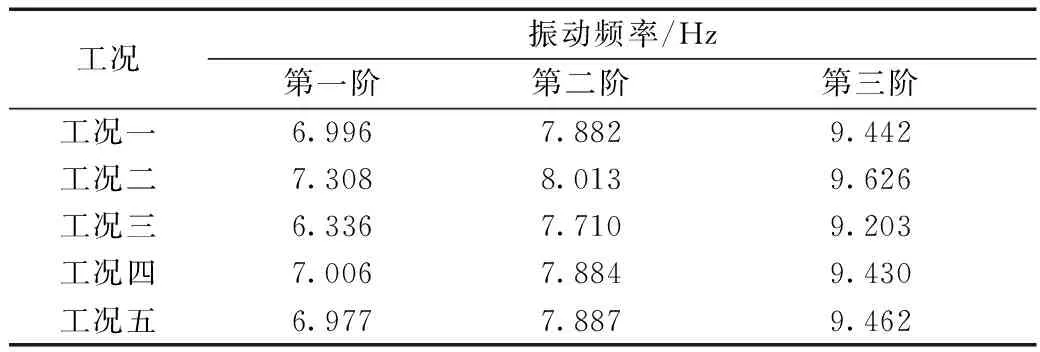
表2 加筋挡土墙三阶段振动频率模拟结果Table 2 Simulation results of vibration frequency of reinforced retaining wall in three stages

图2所示为工况一下的挡墙振型图。工况一计算得到结构体系的第一、二、三阶频率为6.996、7.882、9.442 Hz。工况二条件下，保持泊松比不变，土体弹性模量增大16.7%，计算得到结构体系的第一、二、三阶频率为7.308、8.013、9.626 Hz。工况三条件下，保持泊松比不变，土体弹性模量减小16.7%，计算得到结构体系的第一、二、三阶频率为6.636、7.710、9.203 Hz。

图2 工况一计算结果与振型图Fig.2 The calculation results of working condition 1 and the mode diagram

计算表明，增大土体的弹性模量能够增大结构体系的振动频率。土体弹性模量增大16.7%，第一阶频率增大4.5%、第二阶频率增大1.7%、第三阶频率增大1.9%。反之，减小土体弹性模量则会减小结构体系的振动频率。若减小土体弹性模量16.7%，则体系第一阶频率减小5.1%、第二阶频率减小2.2%、第三阶频率减小2.5%。

同理，从表2可知，工况四、五计算结果发现土体泊松比增大或减小16.7%，结构体系前三阶频率增大(或减小)幅度均不超过0.2%。

综上所述，墙后土体弹性模量增大或减小均能对结构体系的振动特性产生较为明显的影响，但土体泊松比的变化对结构体系振动特性影响极小，而且对结构体系模态的影响也不规律。

3 基于灰关联的影响因素分析

3.1 灰关联分析的基本原理和方法

为进一步分析不同模型参数对加筋挡土墙的影响程度，引入灰关联分析法进行分析。灰色理论常应用于系统中信息不完全，难以确定因素间主次关系的分析过程。通过计算灰色系统中有限数据序列灰色关联度的方法，分析出系统内各影响因素之间的主次关系。从而确定各因素与目标变量之间的密切关系。灰关联分析步骤[12]如下：

(1)确定敏感因子因素序列矩阵及目标序列矩阵。

设有m个影响因素，建立影响因素序列矩阵X为

(6)

式(6)中：m为第i个影响因素的第j取值(取值时应使所选n值遍布影响因素的定义域)。

对应影响因素序列矩阵X的目标序列矩阵Y为

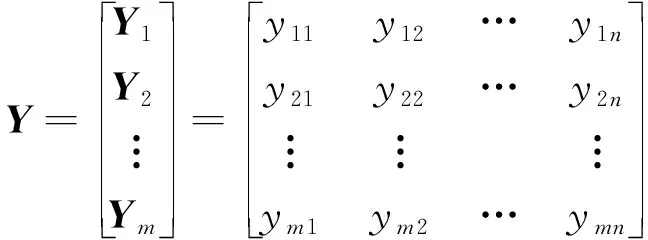
(7)

式(7)中：yij为xij对应的目标。

(2)矩阵的无量纲化。

各因素的量纲不同及数值相差甚远，采用极差变化的方法对数据进行处理，消除因素序列和目标序列的各因素差异，对X进行数值变换可得

(8)

同理，对目标序列Y进行无量纲化处理得

(9)

(3)关联度分析及敏感性评价。

确定矩阵的灰关联差异信息空间为

Δij=|y′ij-x′ij|

(10)

从而得到差异序列矩阵，并在差异序列矩阵中提取差异信息的最大值和最小值：Δmax=maxΔij，Δmin=minΔij。

通过整体分析找出各因素的差异性和相关性，并用关联系数表示为

(11)

式(11)中：η为分辨系数，η∈[0,1]，一般取0.5。

通过计算平均值作为关联度，从而进行影响参数的灰关联比较，关联度计算式为

(12)

在关联度序列中，影响参数所对应关联度相对越大，说明该参数对目标的影响越大，其敏感性越强。

3.2 影响因素的灰关联分析

以弹性模量、泊松比、重度、黏聚力、内摩擦角为影响因素，以振动频率为目标序列，计算各因素与振动频率之间的关联度。灰关联分析序列编号为：X1为弹性模量(MPa)，X2为泊松比，X3为重度(kN/m3)，X4为黏聚力(MPa)，X5为内摩擦角(°)，Y1为第1阶振动频率(Hz)，Y2为第2阶振动频率(Hz)，Y3为第3阶振动频率(Hz)。

根据所选参数影响因素和分析目标列出灰关联分析表如表3所示。分别运用式(10)～式(12)进行计算，得各参数对三阶振动频率的灰关联度计算结果如表4所示。

表3 影响因素与目标序列灰关联分析Table 3 Grey correlation analysis of influencing factors and target sequences

从表4的三阶振动频率的灰关联度分析可以看出：在5种不同的工况下，对加筋挡土墙振动特性影响最大的是土体的弹性模量，其次为内摩擦角，而泊松比、重度、黏聚力参数的变动对加筋挡土墙振动特性的影响较弹性模量、内摩擦角偏小。明确弹性模量、内摩擦角为主要影响因素，有助于研究者对加筋土挡墙振动分析过程中排除对非重要因素的注意力。

表4 各因素与振动频率的灰关联度Table 4 The grey correlation between each factor and the first order vibration frequency

3.3 参数对振动特性影响分析

弹性模量对振动频率的影响如图3所示，由数值模拟计算分析可知，墙后土体弹性模量和内摩擦角的增大或减小均能对结构体系的振动特性产生较为明显的影响，土体弹性模量和内摩擦角增大能够提高结构体系的振动频率，土体弹性模量和内摩擦角增大减小能够降低结构体系的振动频率。弹性模量与振动频率呈线性关系，其中对第一阶的振动影响最明显，对第二阶振动频率影响降低，对第三阶振动频率又有所加强。

图3 弹性模量对振动频率的影响Fig.3 The influence of elastic modulus on vibration frequency

内摩擦角对振动频率的影响如图4所示，内摩擦角与振动频率呈二次函数关系，其中对第一阶的振动影响最明显，二次函数顶点坐标为(32，6.67)；对第二阶振动频率影响降低，二次函数顶点坐标为(32，7.80)；对第三阶振动频率又有所加强，二次函数顶点坐标为(32，9.31)；根据计算模型，振动初期由于内摩擦角的增大，土颗粒有利于稳定并减小加筋挡墙的振动，当达到最小振动频率后，由于土颗粒的非连续性，应力和应增大，振动频率增加。

图4 内摩擦角对振动频率的影响Fig.4 The influence of internal friction angle on vibration frequency

从表4中的数据同时可以发现，土体泊松比、重度、黏聚力的变化对结构体系振动特性影响较小，而且对振动频率的影响也不规律。

4 结论

(1)基于ABAQUS建立加筋土挡墙频率计算模型,计算5种工况条件下结构体系的前三阶频率，发现墙后土体弹性模量对结构体系的振动特性影响较明显，但土体泊松比变化对结构体的系振动特性影响较小。

(2)基于灰关联分析法，以填土弹性模量、泊松比、重度等5个参数为影响因素，以振动频率为目标序列，分析不同因素与目标序列之间的关联度，揭示了加筋挡土墙振动特性对土体的弹性模量变化最敏感，其次为内摩擦角，对泊松比、重度、黏聚力敏感度较低。通过分析敏感因素与振动频率的关系，为加筋挡土墙的设计和研究提供理论参考。

(3)研究了土体弹性模量和内摩擦角对振动特性的影响，发现了土体弹性模量与振动频率呈线性关系；而内摩擦角与振动频率呈二次函数关系，内摩擦角在32°时对频率影响最为敏感。两者在对三阶振动影响的趋势是一致的，即先增加后减小，再增加。

(4)为保证加筋挡土墙较小的自身振动频率，选择填料时应通过试验确定土体弹性模量较小，同时内摩擦角避开32°附近。同时应该合理设计墙后其他填土参数避免结构产生过大振动位移。