对《锐角三角函数》教学问题的再思考
陈方勇 刘清清 阮征 孙业勤


【摘要】以高中生在学习任意角三角函数时常常出现的理解偏差为出发点,分析并探寻出现这种偏差原因,据此提出思考.在借鉴高中学习任意角三角函数的思想基础上,根据初中教材提供的探究材料,以函数的观念看待锐角三角函数的教学,最后强调学习锐角三角函数在初中阶段的必要性所在.
【关键词】锐角三角函数;任意角三角函数;初高中衔接1问题背景
锐角三角函数是初高中衔接教学的体现之一,初中学习的锐角三角函数是高中学习三角函数的基础,高中的锐角三角函数学习是初中所学内容的继续深入和扩展.初中只涉及锐角三角函数和解直角三角形,且知识点少、内容比较简单,而高中研究任意角三角函数的内容丰富复杂,理论性强、实践性广.那么三角函数在不同学段是如何呈现的呢?
以人教版和沪科版的初中教材为例,两者均是在Rt△ABC中,∠C=90°,利用三角形相似,说明“只要锐角∠A的角度不变,∠A的对边与邻边的比值是不会变化的”,接着在直角三角形中利用“比值”给出锐角三角函数的定义.高中以人教版A版为例,教材中以初中定义为引入,由弧度的学习,借助于单位圆对初中锐角三角函数重新定义,接着教材中有这样一段话:锐角三角函数可以用单位圆上点的坐标表示.同样的,我们可以利用单位圆定义任意角的三角函数.最后,教材给出类似于解释说明的一段文字:所以,正弦、余弦、正切都是以角为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,所以我们将它们统称为三角函数[1].由于角的集合与实数集之间可以建立一一对应关系,三角函数可以看成是自变量为实数的函数.认真研读不难发现,最后一段话才是三角函数的本质,高中的三角函数教学的进行是建立在初中的基础上的,那么初中教师该如何进行此内容的教学呢?
2问题的发现与提出
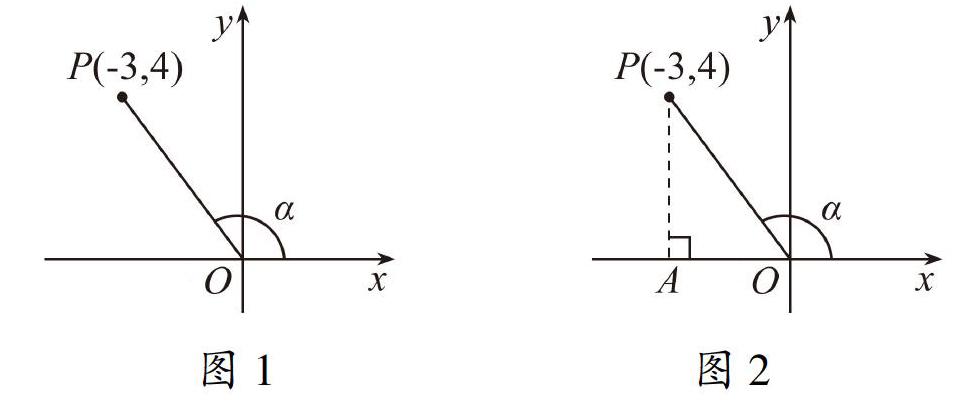
在初中教学时,教师常常以“锐角∠A的角度不变,∠A的对边与邻边(斜边)的比值是不会变化的”为突破口认识与探究锐角三角函数,事实上这种认知是有偏差的,这并不是锐角三角函数的本质.由于初中阶段是通過直角三角形认识和定义锐角三角函数,所以在高中阶段的学习时,学生的思维定势和根深蒂固的思考习惯会不自觉把任意角三角函数的定义局限于直角三角形中,因此对任意角的三角函数定义感到困惑和不解,导致很多学生在学习三角函数这一章时对概念不明确、不能真正理解其含义,乃至在实际运用中因混淆概念而解题失误[1].例如,在高中初次学习tanα(如图1所示),即使教师反复强调任意角的正切函数的定义,但学生的解题习惯依然会停留在图2,因此常常遇到学生困惑地问:为什么比值是负数?教师可能会迫于无奈地说“因为点A在负半轴上,所以OA是负值”——这种解释显然是无稽之谈,更会让学生的认识与理解滑向无底深渊.那么,为什么学生在高中学习时,会出现图2的情形和疑问呢?
3问题分析
陈曦在《HPM视角下“任意角三角函数的概念”教学研究》一文中详细介绍到:教材(人教A版)只是在第一节内容上安排了任意角与弧度制的内容,接下来就用单位圆给出了任意角的三角函数定义,教师的普遍讲法是回顾初中锐角三角函数的定义,然后让学生考虑如何将锐角三角函数推广到任意角三角函数.这种讲法无疑是让学生陷入一个误区,即任意角三角函数是锐角三角函数的推广,自然有很多学生认为任意角三角函数仍然是研究三角形三边关系的工具,只是不再局限于锐角三角形,也有很多学生排斥单位圆的定义,觉得不如初中阶段所给的“比值法”好,既不直观、也难以用来计算[3].于是就出现了开头的图2,产生这一现象主要原因是:(1)教师没有讲明高中阶段学习的三角函数与初中阶段学习的锐角三角函数研究的内容、学习方法和数学思考存在的不同,容易造成学生对于概念的混淆.章建跃对两者的发展历史和区别进行了详细的介绍;(2)学生在初中阶段首次接触锐角三角函数时还没有树立正确的认识观,导致他们狭隘地认为锐角三角函数就是一个“比值”[3].可见这种片面的认知对高中阶段的数学学习有着明显的阻碍作用.既然锐角三角函数是函数,那么教师在教学中就应该找到适切的教学方法,让学生以“函数的眼光”看待“锐角三角函数”、让其具有函数的味道、避免片面的“比值”认识与理解、减少在后续学习中的认知障碍,从而顺利衔接高中阶段的“任意角三角函数”学习.最后,学生初次接触锐角三角函数时,有何折中的办法避免以上的认知误区,让高中学习更为流畅和自然,真正达到学习知识的螺旋式上升,体现出明显的阶段需求呢?以笔者之见,高中教材中“借助于单位圆对初中锐角三角函数重新定义”也许可以缓解初中生对锐角三角函数的认知偏向,为问题的解决提供一种广阔的视角.
4问题解决
高中认识任意角三角函数有两种方法即是“单位圆定义法”和“终边定义法”.按照沪科版的内容编排,锐角三角函数在圆之前,因此利用单位圆认识锐角三角函数已然行不通,所以采用“终边定义法”.
4.1正确认识正切函数的概念
由于锐角三角函数是一种函数,教师在讲解本节课,出发点和落脚点应是对锐角三角函数概念的初步理解,这样才能避免学生对锐角三角函数狭隘的认知.直角三角形只是认知锐角三角函数的一种特殊形式,并不能成为理解锐角三角函数的基石,更不能直接探究“锐角∠A的角度不变,∠A的对边与邻边(斜边)的比值是不会变化的”,前面还需要一些准备工作.笔者根据上述分析,设计沪科版初中数学的《锐角三角函数》教学探究过程.
教师:请同学们看大屏幕,你看到了什么?见图3.
学生(共同):坐标系和线段OA,点A的坐标是(x,y).图3
5教学问题的再思考
既然高中会继续深入学习任意角三角函数,那么初中学习锐角三角函数是否有必要呢?初中阶段为什么要学习锐角三角函数呢?以笔者之见,初中阶段学习锐角三角函数是必不可少的.
5.1知识系统性的必要性
初中阶段,学生解三角形均是转化为直角三角形,利用勾股定理、三角形内角和与锐角三角函数解三角形.勾股定理与三角形内角和分别反映的是三角形三边与三角的数量关系,边和角的数量关系就涉及到锐角三角函数,因此锐角三角函数是解三角形中边角关系的纽带与桥梁,有了该部分的知识,勾股定理与三角形内角和才不会“孤立无援”、才会让解三角形的知识网络更为完整.如此,边、角以及边角关系三者自成一体、互相融合与补充,体现了解三角形知识的系统性.
5.2义务教育阶段的必要性
根据《义务教育数学课程标准(2011年版)》课程性质可了解到:义务教育阶段的数学课程是培养公民素质的基础课程,具有基础性、普及性和发展性.数学课程能使学生掌握必备的基础知识和基本技能,而《课标》对本节的要求是“能用锐角三角函数解直角三角形,能用相关知识解决一些简单的实际问题”[4].锐角三角函数在生活生产、军事、地理、工业、物理等方面都有着广泛的应用,无疑更明确学习锐角三角函数是义务教育阶段学生掌握必备的基础知识与基本技能,锐角三角函数从实际生活中产生,又运用到实际生活中去,因此是必不可少的.
5.3锐角函数与任意角三角函数内容区别的必要性
章建跃《为什么用单位圆上点的坐标定义任意角的三角函数》中对锐角三角函数与任意角三角函数的描述:锐角三角函数是研究三角形各种几何量之间的关系发展起来的,任意角三角函数是研究现实中的周期现象而发展起来的.它们研究的对象不同,表现的性质也不同.我们既不能把任意角的三角函数看成锐角三角函数的推广(或一般化),又不能把锐角三角函数看成是任意角的三角函数在锐角范围内的“限定”[5].由此可见,锐角三角函数与任意角的三角函数同中有异,两者的数学思想、学习方法、学习内容均有差异,并且锐角三角函数易接受、易理解、易掌握,若把锐角三角函数放在高中阶段学习,不仅不符合数学史发展的阶段性,也不符合高中生的认知规律(即学习内容的难度低于学生的认知水平),所以在初中阶段学习锐角三角函数是合情合理的.
6总结
综合以上分析,初中教师完全按照高中学习任意角三角函数的方法教学锐角三角函数是强人所难,并且锐角三角函数与任意角三角函数有一定的区别,所以教师遵照“锐角∠A的角度不变,∠A的对边与邻边(斜边)的比值是不会变化的”进行探究也无可厚非.但站在高中的学生课堂反馈来看,这种直接的探究确实带来了“后遗症”,对学生后续学习产生严重的思考障碍.因此,教师需要在认识锐角三角函数之初,借鉴高中任意角三角函數学习的思想进行探究,对初中的知识进行加工处理,让学生经历一系列的数学活动,亲身经历锐角三角函数的发生、形成、发展的过程,使得学生有相对充足的时间思考、认识、理解锐角三角函数,更好助力高中任意角三角函数的学习.
参考文献
[1]中华人民共和国教育部审定.普通高中课程标准实验教科书(A版)[M].北京:人民教育出版社,2019.
[2]石芮嘉.高中生学习三角函数的困难与解决对策[J].教育观察,2016(10):92-98.
[3]陈曦,张海玲等.HPM视角下“任意角三角函数的概念”教学研究[J].首都师范大学学报(自然科学版),2014(12):23-27.
[4]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2011.
[5]章建跃.为什么用单位圆上的点的坐标定义任意角的三角函数[J].数学通报,2007(1):15-18.

