Metachronal propulsion of non-Newtonian viscoelastic mucus in an axisymmetric tube with ciliated walls

S Shaheen,K Maqbool,R Ellahi,2,∗and Sadiq M Sait

1 Department of Mathematics and Statistics,International Islamic University,Islamabad,Pakistan

2 Fulbright Fellow,Department of Mechanical Engineering,University of California Riverside,CA,United States of America

3 Center for Communications and IT Research,Research Institute,King Fahd University of Petroleum &Minerals,Dhahran-31261,Saudi Arabia

Abstract Cilia-induced flow of viscoelastic mucus through an idealized two-dimensional model of the human trachea is presented.The cilia motion is simulated by a metachronal wave pattern which enables the mobilization of highly viscous mucus even at nonzero Reynolds numbers.The viscoelastic mucus is analyzed with the upper convected Maxwell viscoelastic formulation which features a relaxation time and accurately captures normal stress generation in shear flows.The governing equations are transformed from fixed to wave (laboratory) frame with appropriate variables and resulting differential equations are perturbed about wave number.The trachea is treated as an axisymmetric ciliated tube.Radial and axial distributions in axial velocity are calculated via the regular perturbation method and pressure rise is computed with numerical integration using symbolic software MATHEMATICA‘TM’.The influence of selected parameters which is cilia length,and Maxwell viscoelastic material parameter i.e.relaxation time for prescribed values of wave number are visualized graphically.Pressure rise is observed to increase considerably with elevation in both cilia length and relaxation time whereas the axial velocity is markedly decelerated.The simulations provide some insight into viscous-dominated cilia propulsion of rheological mucus and also serve as a benchmark for more advanced modeling.

Keywords: viscoelastic mucus,ciliated surface,trachea,inertial flow,axisymmetric tube,rheology flow

Nomenclature

1.Introduction

Historically the Dutch microscopist van Leeuwenhoek first discovered cilia in the late 17th century [1].Cilia motion contributes a pivotal role in many physiological processes including alimentation,inner-ear bio-acoustics,circulation,locomotion,respiration and reproduction [2,3].The cycle of beat of a single cilium is separated into the effective and the recovery stroke and during the recovery stroke the curvature starts to move towards the cilium shaft until it returns to the original position before the start of effective stroke [4–7].The hydrodynamic coupling encourages adjacent cilia to beat with a fixed phase relationship to one another.A field or row of cilia beating in this manner is said to be metachronism.The collective two-stroke motion of cilia has been investigated in many biological and psychological studies [6,8].Motile cilia are found in the lining of the human trachea(windpipe),where they sweep mucus and foreign matter out of the lungs.A very sophisticated hydrodynamic-structural interaction therefore occurs between cilia and biological liquids which is critical to efficient propulsion of these liquids.This has therefore attracted considerable attention in recent years.Interesting studies in this regard which have used both mathematical and computational models include Dauptain [9] and Guo [10].Two popular approaches have emerged for describing analytically the flexible motion of cilia,namely,the sub-layer and the envelope model approach[11,12].Since a single cilium depends on the effective and recovery strokes therefore different models have been proposed to describe the cilia motion.When metachronal waves propagate in the direction of the forward stroke this is referred to as a symplectic beat pattern whereas when they propagate in the opposite direction this is termed as an antiplectic beating pattern.Both types of cilia motion also arise in embryonic development and in chemo-mechanical signal relaying in other physiological functions.Rikemenspoel and Ruder[13]showed that cilia perform planar vibrations.Gueron et al [14],Holwill [15] and Mitran [16] developed threedimensional models of cilia beating in which forces and momentum transfer are dictated by the position of cilia and their velocity.Rydlolmet et al[17]used a finite element approach to compute the influence of biophysical,geometric and structural characteristics such as cilia length,bending and membrane resistance on ciliary movement,and showed that inhibition of ciliary activity may lead to diseases of respiratory tract.

Knight-Jones et al [18] showed that symplectic waves dominate in biological liquids characterized by higher viscosity or viscoelastic behavior.Lauga et al [19] much later showed that tracheal cilia dynamics features symplectic waves used to propel viscoelastic mucus.In the human trachea,the symplectic waves achieve high efficiency since the cilia undergoing an effective stroke,and generates the larger forces necessary to overcome the higher fluid resistance associated with viscoelastic properties of the mucus.Mucus is in fact a gel comprising water,high molecular weight glycoproteins (mucuins) mixed with serum and cellular proteins and lipids.A detailed knowledge of muco-ciliary clearance is important for the correct diagnosis and treatment of respiratory tract diseases (including asthma,diffuse bronchitis,cilia infections etc,[20]) and essential for sustaining the correct beating frequency and coordination of cilia motion.Vasquez et al[21]have described a viscoelastic fluid model for mucus which is dependent upon temperature,mucus gel,periciliary hydration and mucus beating frequency of cilia.The Newtonian viscous fluid model is therefore inadequate for representing mucus rheology.Viscoelastic models are required in mucus propulsion simulation and examples of such models include the Oldroyd-B quasi-linear model by Norouzi et al[22],Sisko model by Ali et al[23],FENE-P(finite extensible nonlinear elastic)model by Norouzi et al [24],Jeffery model by Narla et al [25],upper convected Maxwell model by Tripathi et al [26] and Williamson model by Shamshuddin et al[27],all of which have been applied extensively in many areas of non-Newtonian biofluid dynamics including pharmaco-dynamics,blood flows,digestive transport and biotribology.These models feature different capabilities include retardation,relaxation,normal stress differences,deformation memory and shear-thinning behavior.In the area of ciliated propulsion,numerous simulation studies have also been communicated.Maqbool et al [28,29] employed the Jeffrey and generalized viscoelastic model to study cilia propulsion in a tilted conduit.Ashraf et al [30,31] used a third grade Reiner-Rivlin differential model and Johnson–Segalman to investigate the peristaltic-cilia dynamics in embryology.

The rheological properties of mucus for muco ciliary clearance is addressed by Norton et al [32] (linear Maxwell model),also UCM model has been described extensively in biological fluid mechanics by Tripathi and Bég [33] (peristaltic intestinal flows),Abbasi et al [34] (endoscopic flows)and Narla et al [35] (embryological transport),recently,few studies [36–39] also described the fluid viscosity of different non-Newtonian fluid models and their applications in biomedical engineering.

In the present study,a mathematical model is developed for metachronal propulsion of non-Newtonian mucus in an axisymmetric tube with ciliated walls.The UCM model is implemented for the mucus rheology which to the authors’knowledge has not yet been explored explicitly in ciliated propulsion and it is the most fundamental building block that accounts for stress relaxation versus time.When mucus is deformed abruptly by cilia,the relationship between stress and strain tends toward the elastic behavior of a solid.The simplest viscoelastic fluid model that allows for elastic behavior on short time scales is the upper convected Maxwell(UCM) constitutive equation,which relates the rate of strain and stress [40].The governing partial differential equations for mass and momentum conservation are reduced via a stream function.Perturbation solutions are developed for the velocity field,stress,pressure flux and a numerical integration routine is deployed to compute pressure difference.The influence of cilia length parameter and Maxwell rheological parameter(relaxation time)on pressure rise,pressure gradient and velocity distribution is visualized graphically and interpreted at length.It is envisaged that the results of the current article may be beneficial in further elucidating the hydrodynamics of human muco-ciliary propulsion.

Figure 1.Model for axisymmetric mucus ciliated propulsion in trachea.

2.Mathematical model

The physical model approximation to the human trachea is shown in figure 1.We consider the flow of an incompressible,upper-convected Maxwell (UCM) fluid (mucus) in a tube having diameter 2h.An infinite number of continuously beating adjacent cilia are present along the internal wall surface of the tube and they collectively generate a symplectic metachronal wave which moves in the direction of the longitudinal direction with wave speed c.This generates fluid motion and the sustained whip-motions propel the mucus downstream.The elliptic envelope model [41,42] is adopted for which the motion of tips of cilia are assumed to trace elliptic paths.The continuity and momentum equations for Maxwell viscoelastic mucus ciliated propulsion through the axisymmetric tube in a cylindrical coordinate system (r,z)[26] may then be written as:

Here the appropriate stress tensors for the upper-convected Maxwell viscoelastic model are defined as [33,34]:

The velocity vector in equation(2)for axisymmetric flow in the ciliated tube takes the form:

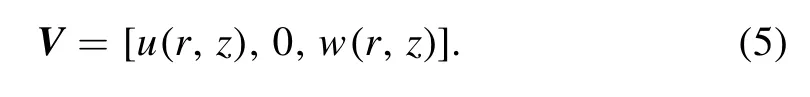
Implementing the appropriate component terms from the tensors in equations (3) and (4) into the conservation equations (1) and (2),the partial differential forms of the relevant equations emerge as:

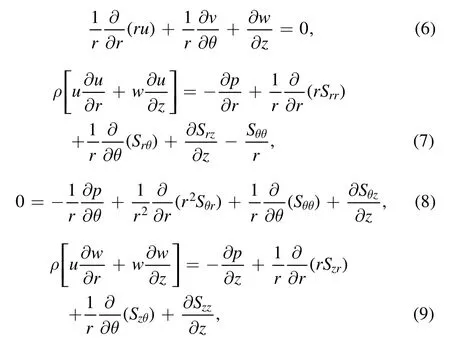
where the shear and normal stresses satisfy the following expressions:

To normalize the above equations,the following nondimensional parameters are introduced:

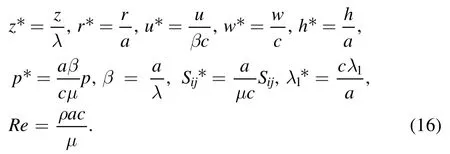
Here z*denotes dimensionless axial coordinate,r*denotes dimensionless radial coordinate,w*is dimensionless axial velocity,h*is dimensionless radius of the tube,p*is dimensionless hydrodynamic pressure,β is dimensionless wave number,S*ijis the non-dimensional stress tensor,λ1is Maxwell relaxation time parameter,Re is Reynolds number,a is radius of the cylindrical tube,λ is metachronal wavelength and c is the wave speed.After using equation (5) and dropping the asterisk notation for dimensionless quantities,equations (6)–(15) in non-dimensional form are:

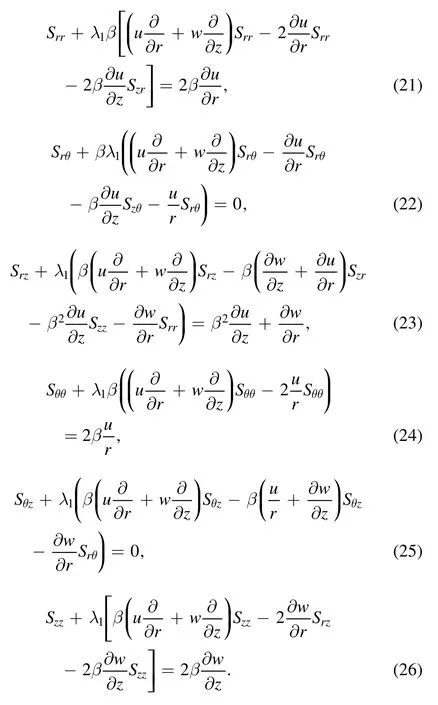
To reduce the unknowns,it is judicious to define a dimensional stream function for equations (17)–(26)

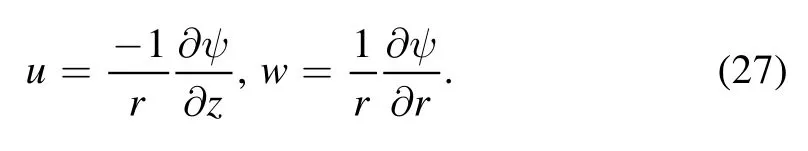
Equation (17) is identically satisfied and equations (18)–(26) are transformed to:

eliminating the axial pressure gradientand radial pressure gradientsfrom equations (28),(29) yields:

Here:

The volumetric flow rate can be defined in the inertial frame as:

in the laboratory(wave)frame volumetric flow rate becomes:

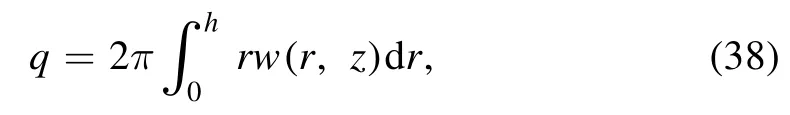
using equations (17),(36) and (37),we obtain:

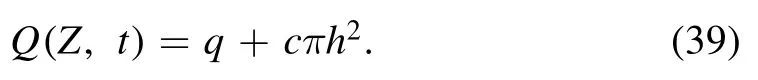
The mean-time volumetric flow rate can be defined as:

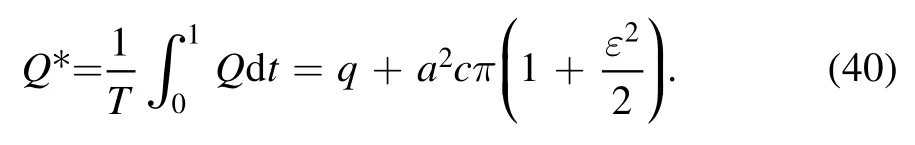
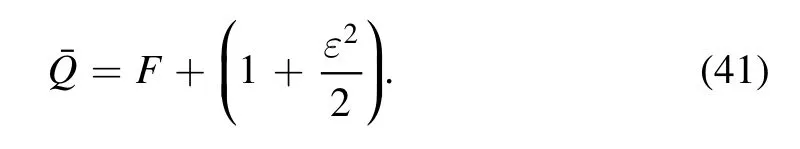
Following boundary conditions are chosen as used in[41]:

3.Perturbation solutions

To find the solution of nonlinear system of partial differential equations mathematician used analytical and numerical methods[42,43],but mathematical analysis might be easy by analytical method therefore,in this study we use perturbation method to find the solution for velocity and pressure rise.In this method we expand the stream function ψ,pressure distribution p,stress S and flux F in power series of small parameter (wave number) β ≪1:

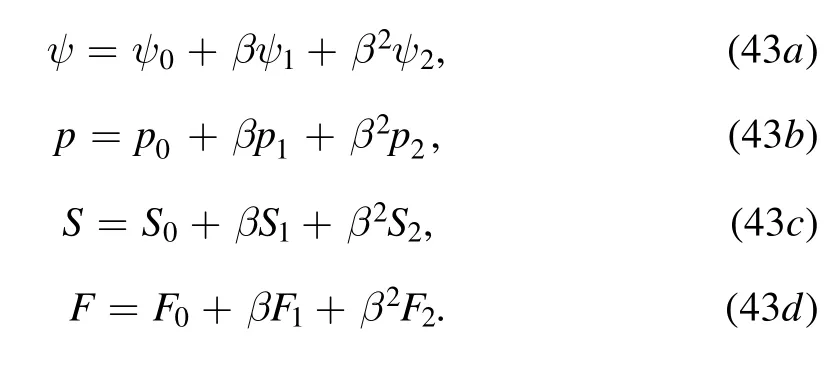
3.1.Zeroth order solution

After lengthy algebraic calculations,the following boundary value problems for the stream function,pressure gradient and stress components can be derived

Here a11is a constant defined as:

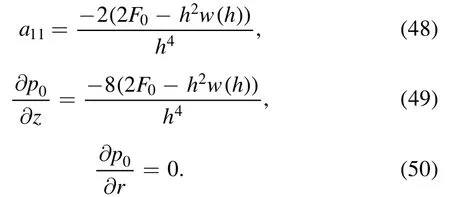
Pressure rise per wavelength can be calculated as:

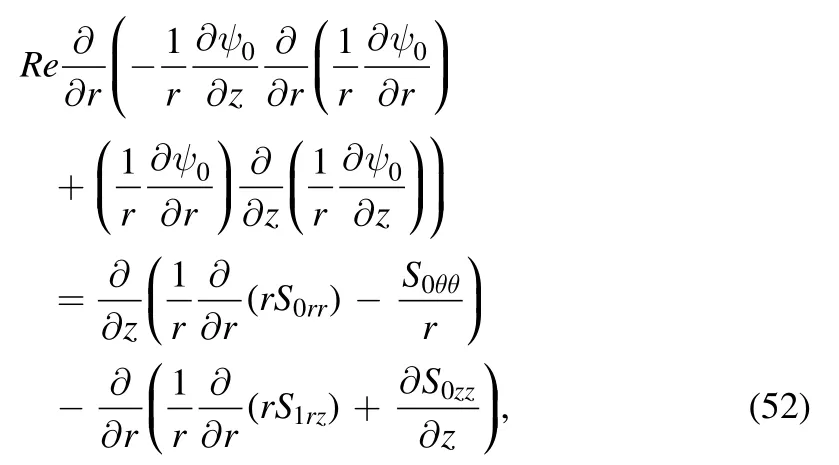
The relevant boundary conditions are:

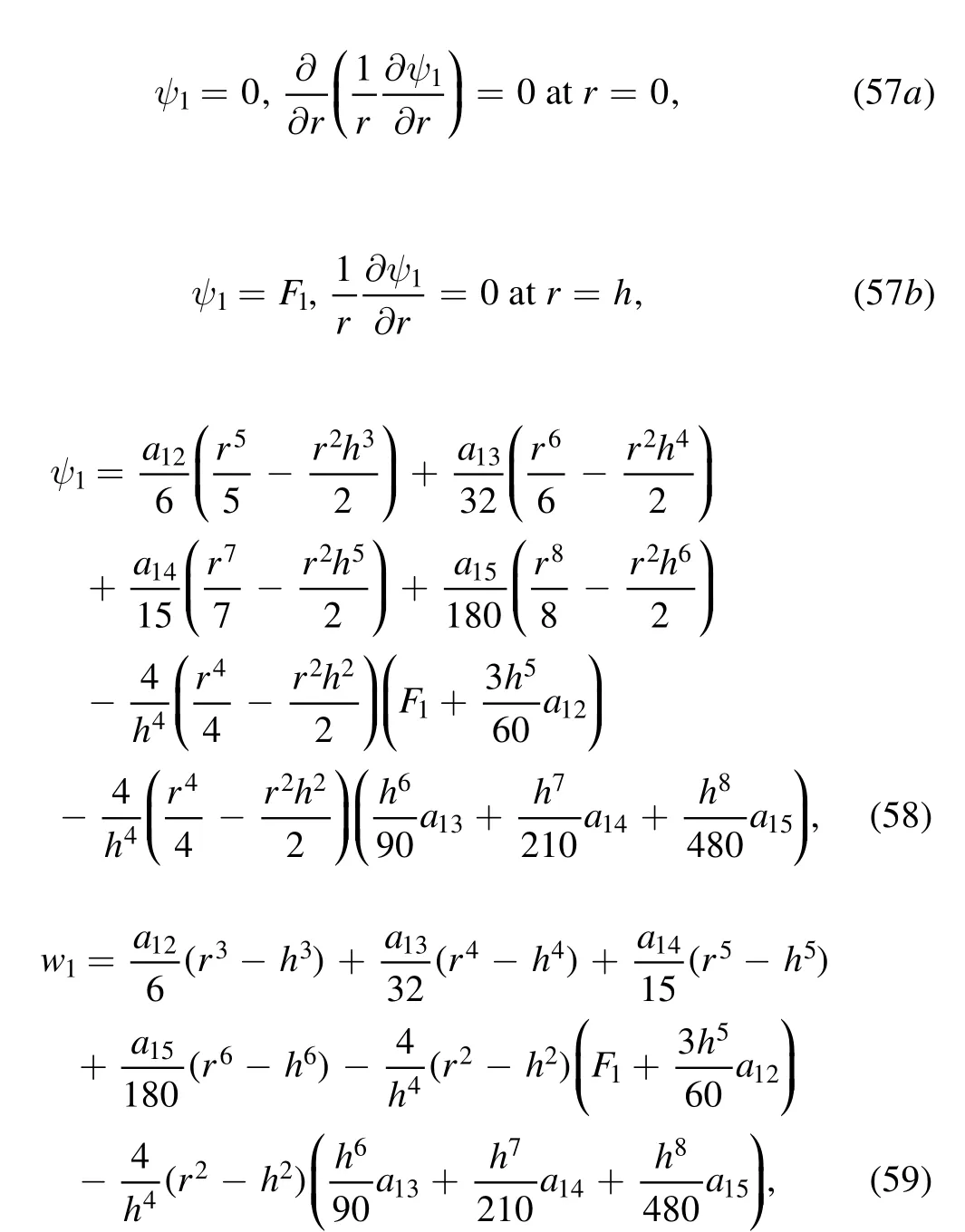
3.2.First order solution

where a12,a13,a14,a15are constants defined as follows:

Substituting equations(46),and(58)–(63)in(53)we getwhich is calculated by using software MATHEMATICA‘TM’.

Integrating equation (64) we get pressure rise

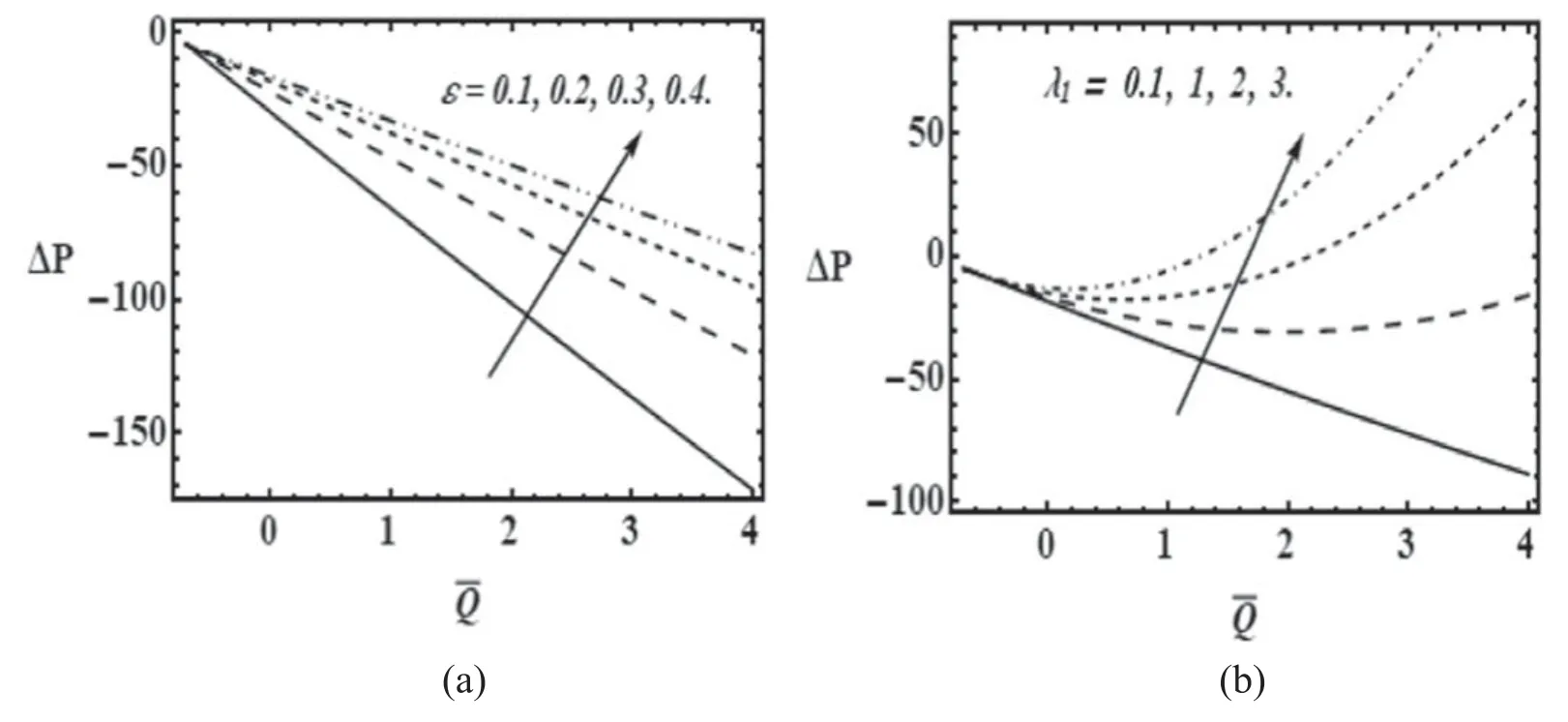
Figure 2.Variation of pressure rise for (Δp) with time averaged flux (Q-) for α=0.2; Re=0.01 with (a) β=0.01; λ1 =0:1 for various values of cilia length parameter (ε) and (b) β = 0:01; ε=0:2 for various values of relaxation time (λ1).

Figure 3.Variation of axial pressure gradient(dp/dz)with z for α=0.2;Re=0.01 with(a)β=0.01;λ1=0:1 for various values of cilia length parameter (ε) and (b) β=0.01; ε=0.2 for various values of relaxation time (λ1).

4.Graphical results

The graphical representation of pressure rise,Δp,with dimensionless mean-time volumetric flow rate(time averaged flux),Q-; for various values of cilia length ε; and Maxwell relaxation time(λ1),are shown in figures 2(a)and(b)keeping all other parameters fixed as suggested in [41]

Inspection of figure 2(a) reveals that there is a linear decay in pressure drop with increasing time averaged flux at all values of cilia length parameter.However,from figure 2(b)it is evident that only at small relaxation time (λ1=0.1),there is an inverse linear relationship between pressure rise and time averaged flux; for λ1＞0.1,the pressure rise become increasingly parabolic i.e.nonlinear.When relaxation time diminishes the mucus becomes Newtonian.The relaxation time is the characteristic time in which a viscoelastic liquid (mucus) relaxes under changes in external conditions.The mucus is deformed under motion and the characteristic time required for it to relax from a deformed state to its equilibrium configuration is the relaxation time.With higher values of this parameter,the viscous forces are smaller compared with elastic forces.The values studied i.e.0.1≤λ1≤3 are representative of typical shear behavior in tracheal mucus as noted by King [44].In muco-ciliary propulsion the airway surface liquid (ASL) (which protects the airway epithelium from inhaled pathogens and particulates)features a strong viscoelastic behavior.Thus,dependence on viscoelasticity is consistent with observations that airflowmucus interaction and wave formation are impeded by elasticity which manifests in pressure rise in the trachea (tube model).A natural balance in viscosity and elasticity is required in healthy mucus to achieve efficient ciliated-propulsion and avoid inordinately high pressure rise.Weakly viscoelastic behavior is therefore more desirable for ciliated propulsion compared with a high viscoelastic behavior.This may also be related to the inherent coughing problems associated with denser mucus during respiratory infections which also manifests in higher pressure differences and the requirement to generate greater forces to clear the trachea[45].It is also evident that with increasing cilia length parameter (figure 2(a)) there is a substantial elevation in pressure rise.Longer cilia therefore generate greater pressure difference in the tube.This may be due to an increase in force required over the length of the cilia to sustain propulsion.This will result in an increase in pressure rise over all values of time averaged flux.An optimal cilia length is usually present in a healthy trachea [44] which achieves sufficient pressure rise to facilitate propulsion with minimal effort.Pressure rise is also observed in figure 2(b)to be significantly elevated with increasing Maxwell relaxation time.The corresponding boost in mucus elasticity with larger relaxation times induces significant resistance to the cilia motion.This also elevates the pressure difference in the tube.As noted earlier,strong viscoelastic mucus is usually associated with infections in the respiratory system and is therefore undesirable since greater pressure differences correspond to a retardation in mucus propulsion [45].It is also worth noting that in a more sophisticated model of the actual human trachea the ASL is positioned adjacent to a thin traction layer which also plays a vital role in cilia-mucus engagement and propulsion.Although this has not been considered in the current study it offers an interesting extension to it.

Figure 4.Variation of axial velocity(w)with radial coordinate(r)for α=0.4;Re=0.01 with(a)β=0.01;λ1=0.1 for various values of cilia length parameter (ε) and (b) β=0.01; ε=0.1 for various values of relaxation time (λ1).

Figures 3(a) and (b) visualize the impact of cilia length(ε) and relaxation time (λ1) on axial pressure gradient distributions against axial coordinate (z).Figure 3(a) shows that pressure gradient increases with higher values of cilia length i.e.greater length of the cilia generates elevated resistance to the mucus flow which results in increasing pressure gradient in the axial direction.The effect is particularly prominent at intermediate distances along the z-axis.At the extremities i.e.entry and exit points in the ciliated tube the reverse effect is computed.In these peripheral zones there is a clear but weaker reduction in axial pressure gradient with increasing cilia length.It is possible that since there must exist hydrodynamic entry length for low values of z,the mucus flow is not fully developed here and the cilia action is initially assistive to incoming mucus.A similar effect may be apparent at the exit.However,in the main body of the flow,the increment in cilia length will induce an undesirable pressure rise which will be counter-productive to mucus propulsion.Intermediate values of axial pressure gradient will induce optimal flow velocity along the tube which will not be attained when the cilia length exceeds a critical value[45].If the cilia penetrate the mucus only during the effective stroke,this provides a much more direct mechanism for mucus propulsion.However,if the penetration is too deep i.e.excessive cilia length,this inhibit propulsions and lead to excessive pressure rise as observed in figure 3(a).

With increasing value of relaxation time there is as noted earlier,an increase in mucus elastic properties.These impede the cilia metachronal propulsion.Figure 3(b) shows that for the initial region along the tube there is a boost in axial pressure gradient with Maxwell relaxation time,whereas with further distance along the tube the contrary response is computed.As elaborated in earlier discussion,the propulsion of mucus is quite sensitive to the form and state of the mucus.It is known based on experiments,that optimum propulsion is achieved when the concentration of glycoprotein is close to that of the gel transformation phase in mucus [45].Since healthy mucus contains glycoproteins (long chain polymers),viscoelastic behavior is inevitable.However,at excessively higher concentrations of these glycoproteins,the mucus begins to morph into a gel network where elastic forces dominate rather than viscous forces.This leads to a pressure gradient rise with higher relaxation times.However,with further distance from the hydrodynamic entry zone,the gel may achieve a relaxed state (even during metachronal propulsion) and this may lead to a reduction in axial pressure gradient as observed in figure 3(b).

Figures 4(a) and (b) present the radial distributions for axial velocity for various values of cilia length (ε) and relaxation time (λ1) parameter.Increasing cilia length clearly induces a strong deceleration in the axial flow across the entire tube cross-section (figure 4(a)).As described above,the main influence of longer cilia geometries is to impede axial flow due to the greater resistance.As noted earlier this also leads to boost in pressure difference.Smaller cilia length therefore are more assistive to efficient axial flow and metachronal propulsion is optimized in the trachea with smaller cilia rather than larger ones [44–46].Similarly,an increase in relaxation time produces considerable retardation in the flow since elastic forces begin to dominate the viscous forces and the mucus takes longer to return to its relaxed state after deformation.There will also be an associated elevation in pressure difference as a result of this flow deceleration which has been computed in earlier graphs.Weak viscoelastic mucus (as observed in healthy tracheal mucus [44]) generates maximum velocity magnitudes.It is also of interest that even with high relaxation time (or indeed cilia length) the flow is never reversed i.e.back flow is not induced as testified to by the consistently positive values of axial velocity in figures 4(a) and (b).Overall it may be concluded that there is an intimate relationship between cilia length,mucus viscoelasticity and optimized metachronal propulsion in healthy trachea.

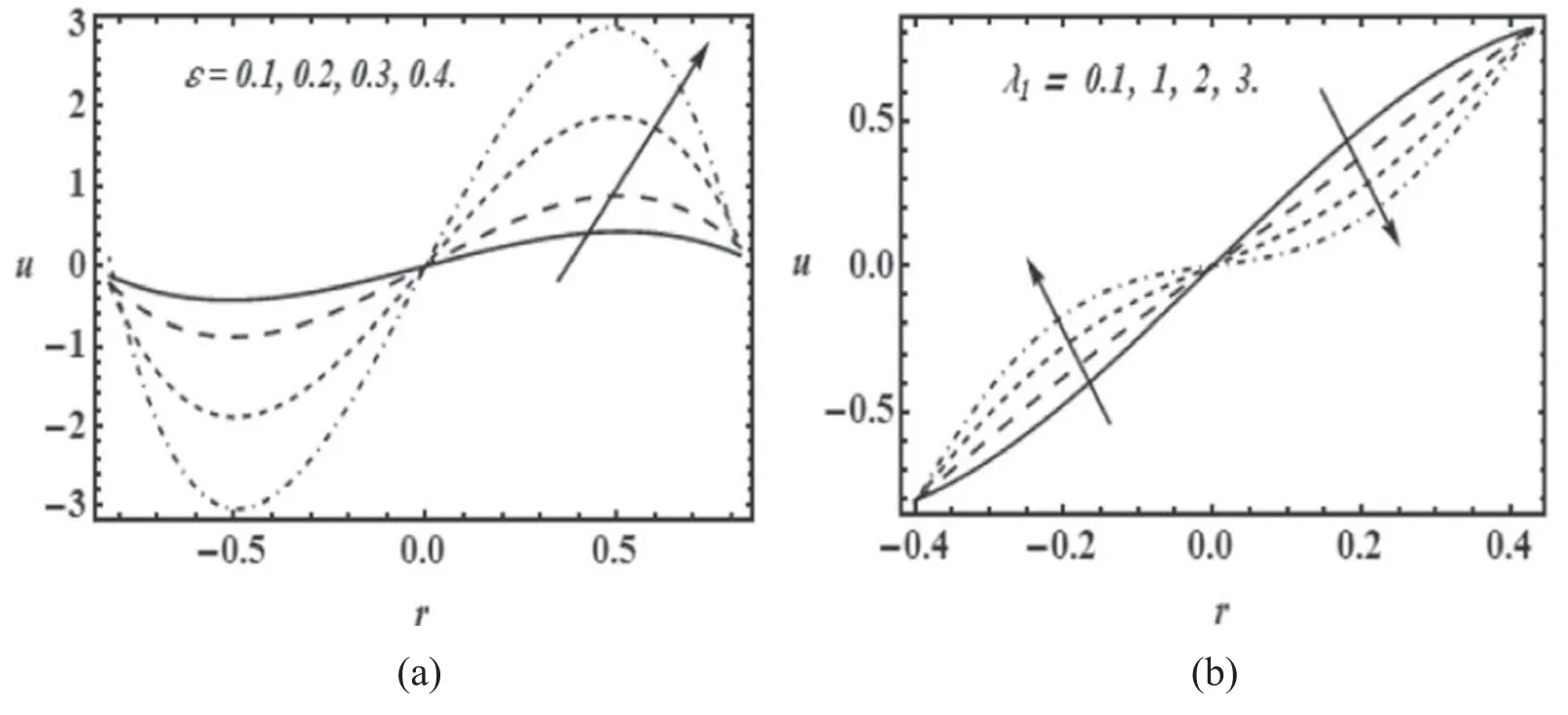
Figure 5.Variation of radial velocity(u)with radial coordinate(r)for α=0.4;Re=0.01 with(a)β=0.01;λ1=0.1 for various values of cilia length parameter (ε) and (b) β=0.01; ε=0.1 for various values of relaxation time (λ1).

Figure 6.Variation of shear stress (Srz) with axial coordinate zr) for α=0.4; Re=0.01 with (a) β= 0.01; λ1 =0.1 for various values of cilia length parameter (ε) and (b) β = 0.01; ε=0.1 for various values of relaxation time (λ1).

Figures 5(a) and (b) present the radial component of velocity distributions for various values of cilia length(ε)and relaxation time (λ1).Increasing cilia length clearly induces acceleration in the radial flow across the entire cross-section(figure 5(a)).The large values of cilia length shows that the force applied on the fluid flow is high that causes to propel the mucus with large speed that is the normal condition of mucociliary in the human trachea but due to different factors when cilia do not get it full length that results into slow movement of mucus.Figure 5(b) shows that an increase in relaxation time produces considerable retardation in the flow since elastic forces begin to dominate over the viscous forces and the mucus takes longer time to return to its relaxed state after deformation.The increase in relaxation time make the mucus thick and the viscosity of the fluid rises that resist the fluid flow therefore the velocity profile decay in the tube.

Figures 6(a) and (b) present the effect of cilia length (ε)and relaxation time (λ1) on shear stress.It is observed that near the entrance and exit region of tube large length of cilia helps to reduce the amount of shear forces required for the mucus propulsion but near the center of tube high values of cilia length requires high amount of shearing forces for the mucus propulsion.Figure 6(b) display that from the inlet to the center region of the tube shearing forces rises with the increase of relaxation time but after that it decays due to the high viscosity of the mucus.

Figures 7(a)and(b)shows the comparison of symplectic and antiplectic wave patterns in radial and axial component of velocity for different values of relaxation time (λ1).It is observed that symplectic wave pattern is more efficient than antiplectic wave pattern in both axial and radial component of velocity for growing values of relaxation time(λ1).Therefore,in the present study we have used the symplectic wave pattern for the mucus propulsion in the ciliated tube.

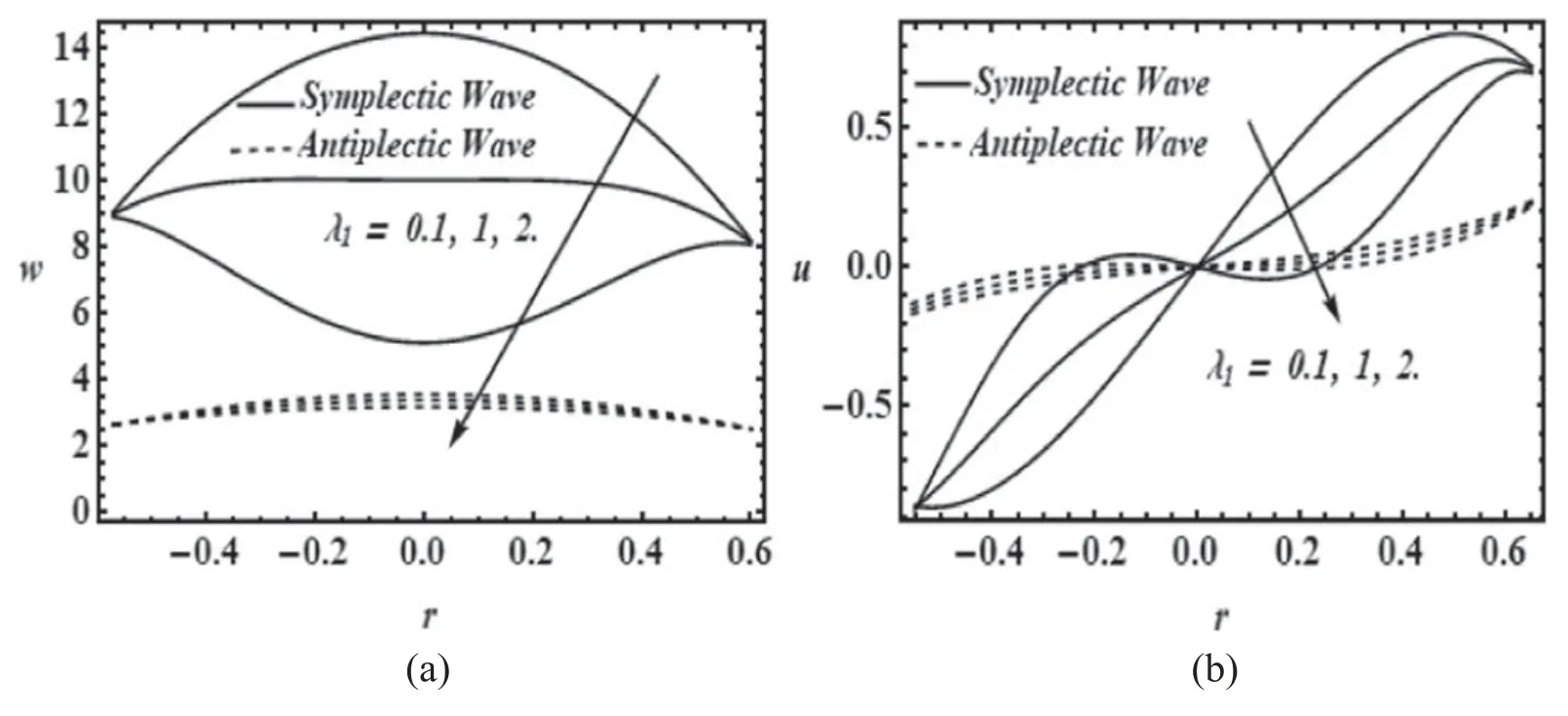
Figure 7.Comparison of symplectic and antiplectic wave for different values of λ1.

5.Conclusions

Motivated by providing a deeper insight into the mechanics of cilia-induced flow of mucus in the human trachea,a mathematical model has been developed for metachronal wave propulsion of viscoelastic mucus in an axisymmetric ciliated tube at moderate Reynolds numbers.An elliptic envelope cilia model and the upper-convected Maxwell (UCM) viscoelastic model have been deployed.The governing equations have been transformed from the fixed to the wave(laboratory)frame with appropriate variables.We have considered the effect of non-zero Reynolds’ number and resulting equations are perturbed about wave number.Perturbation solutions for the velocity field have been derived and numerical integration employed to compute pressure rise in the tube.The perturbation solution is compatible with the boundary conditions that can be visualized by the graphs of velocity profile and pressure rise.The influence of selected parameters i.e.cilia length (ε) and Maxwell viscoelastic material parameter i.e.relaxation time (λ1) for prescribed values of wave number have been presented via graphs.The study has shown that:

I.There is an inverse relationship between time averaged flux and pressure rise for different cilia lengths;however,this relationship is modified to a parabolic one for higher values of Maxwell viscoelastic relaxation time parameter (stronger elastic behavior).

II.Axial velocity decelerated by increasing the cilia length parameter,but pressure rise and pressure gradient rises by the high values of cilia length parameter during the muco ciliary process.

III.Axial velocity decelerated by increasing the Maxwell fluid parameter that causes to increase the viscosity of fluid and shear rate,but pressure rise and pressure gradient rises by the large values of Maxwell parameter that shows more pressure is required for the muco ciliary flow.

IV.The computations are consistent with experimental studies in which it has been shown that undesirable high viscoelasticity inhibits efficient metachronal propulsion of mucus in the trachea and this may be due to respiratory infections and more elastic mucus constitution which cannot propel easily with an associated reduction in cilia beat efficiency.

The present study has shed some light onto the intricate relationship between cilia beating,cilia length and mucus viscoelasticity in ciliated propulsion through an idealized model of the human trachea.However,it may be refined in a number of ways including the simulation of airflow-mucus interaction via computational fluid dynamics and also the implementation of microstructural rheological models (e.g.micropolar model)which may reveal further characteristics of non-Newtonian mucus behavior.It is envisaged that these will be explored in the near future.