Coexistence and fluctuations phenomena with Davidson-like potentials in quadrupole–octupole deformed nuclei

M M Hammad,W H Mansour,E M El-Maghraby,H A Motaweh and Ayman A Aly

1 Faculty of Science,Mathematics Department,Damanhour University,Egypt

2 Faculty of Science,Physics Department,Damanhour University,Egypt

Abstract The energy spectra of three types of two-dimensional potentials (we will call them ‘Davidson-like potentials’ (DLPs)),characterized by four minima separated by barriers,are investigated.The predictions for spectra and wave functions are obtained by using the nine-point finite-difference method.For these potentials,with the existence of a single configuration,a transition of spectra,as a function of barrier height,is covered from tunneling splitting modes to fluctuations phenomena,with equal peaks wave functions,crossing to the spectra of purely anharmonic oscillator potentials(AOPs).A different type of phase transition occurs when two(or more)configurations coexist.With the change of the parameters,a transition of spectra is covered from coexistence phenomena of two distinct quantum tunneling modes to fluctuations phenomena,with unequal peaks wave functions,crossing to the spectra of purely AOPs.Using DLPs,a particular application of the coherent quadrupole–octupole model to describe energy bands with alternating parity of the nuclei 100Mo,146,148Nd,148,150Sm,220Ra,220,222Rn,and 220,222Th is presented.The global parametrization of the model for the selected nuclei is achieved.

Keywords: quantum phase transitions,fluctuations phenomena,coherent quadrupole–octupole motion model,coexistence phenomena

1.Introduction

In nuclear physics,the quantum shape-phase transition (QSPT)has received much interest in recent decades [1–12].QSPTs are abrupt changes within the structure of the energy spectrum,caused by a change in the parameters of the quantum Hamiltonian.With QSPT,the concept critical point[3–8],based on very simple shaped potentials,describes the dynamical symmetry of the nuclear system at points of QSPT between various phases.Up to now,the studies based on these potentials concentrate on the studying of the QSPTs and their critical points,however,during the past three years,a new approach has been proposed for the sake of shape coexistence phenomena and shape fluctuations phenomena [9–12].This new direction is based on the introduction of a barrier that separates two(or more)configurations of states.By changing the barrier height,one can have coexistence phenomena or fluctuations phenomena.This behavior could be achieved by anharmonic oscillator potentials (AOPs)with sextic anharmonicity.By the separation of variables,these problems are reduced to solve the one-dimensional Schrödinger equation.

Recently [13],we extended these type of results to a twodimensional space and test the ability of three types of twodimensional potentials in generating the advantages of the infinite square well potential (ISWP).Actually,the potential for a QSPT at the critical point possesses nearly flat shape.These potentials are characterized by the existence of barriers in its structure and can evolve from a very narrow deformed minimum separated by high barriers to a near flat case,depending on a few parameters.For these potentials,when the tunneling is taken into consideration,the levelEsplits into four levels,E1,E2,E3andE4,i.e.the states appear as closely spaced quartets.We will call this mode of the system tunneling splitting mode (TSM).The quantum tunneling strength among the four minima is determined by the features of the separating barrier.The fluctuations phenomena take place when the wave function peaks begin to combine and join together,but yet distinguishable.This circumstance is obtained when the potentials are symmetric and the tunneling is strong.

In the first part of this work,we shift the analysis from the one that focuses on ISWP and critical points to one that focuses on harmonic oscillator potential (HOP).To this end,first,we introduce three categories of two-dimensional Davidson-like potentials(DLPs)and investigate their ability in reproducing the properties of the HOP and AOPs.They present a transition of spectra from TSM to fluctuations phenomena ending with the spectra of the HOP or AOPs,depending on the height of the barrier.On the contrary,these potentials can evolve from wide spherical minima separated by high barriers to a near flat case or HOP.Moreover,we give an explanation of the coexistence phenomena of two tunneling splitting configurations in twodimensional space based on these potentials.

On the other hand,the dynamical octupole correlations have attracted special focus because they are the cornerstone in the explanation of many negative parity states like the−1 states in the spectra of even–even nuclei that are considered as important indicators of the reflection-asymmetric nuclei[14–20].The main benchmark of whether a nucleus is octupole deformation or not is the existence of the negative-parity band,Lπ= 1−,3−,5−,… ,located nearby the ground-state band and building together a single band withLπ= 0+,1−,2+,3−,4+,… .whilst the positive-and negative-parity bands remain separated from each other,for nuclei in vibration regions.A diversity of methods and techniques were utilized to study the role of the octupole degree of freedom.These include density functional models [21–23],interacting boson and boson vector models [24,25],and collective models,such as the coherent quadrupole–octupole model(CQOM) [26,27].

In the second part of this study,using CQOM,the DLPs are used for studying the yrast and non-yrast energy bands with alternating parity in100Mo,146,148Nd,148,150Sm,220Ra,220,222Rn,and220,222Th.We study the physical consequences of the two-dimensional oscillations with respect to the quadrupoleβ2and octupoleβ3variables.Good agreement has been found between the calculated and measured spectra.A detailed comparison with the predictions of HOP and DLPs is performed.The global parametrization for selected nuclei is achieved.The results of our investigation show that the existence of the barrier is essential in any description of octupole deformed nuclei.Consequently,DLPs provide an extended version of the CQOM which having the ability to reproduce the spectra in even–even quadrupole–octupole shape deformed nuclei.

In section 2,the fluctuations phenomena and coexistence phenomena in two dimensions are analyzed using three classes of DLPs.Section 3 is devoted to a discussion of the CQOM applications in different regions in the nuclear landscape and the numerical results.Section 4 summarizes the results of our work.

2.Fluctuations and coexistence phenomena in two dimensions

In[13],we studied the energy spectra of three types of AOPs which play an essential role in nuclear structure and exhibited multi-dimensional quantum tunneling.These potentials are

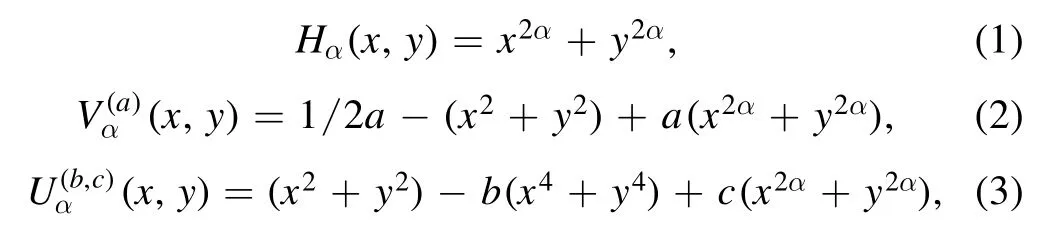
wherea,bandcare free parameters andα= 2,3,4.The predictions for wave functions and spectra are obtained by using the nine-point finite-difference method(for more details see[13]).It has been demonstrated that the purely AOPs,αH,provide a‘bridge’between the HOP and ISWP.Furthermore,the evolution of energy spectra of the AOPs,andas a function of barrier height and normalized to the ground state energy,shows that the transition is changed from TSM to fluctuations phenomena passing by theαHspectra ending with the spectrum of the ISWP.

The AOPs,αH,,and ISWP are appropriate for the transition between two quantum phases,particularly,if one of the phases is related to HOP and simultaneously offer new features.The ISWP is the most important one because of its simplicity and analytic solvability.The purely AOPs,H2,H3,andH4,change from the HOP to the ISWP,respectively.Here,we focus our attention on the purely AOPsHαbecause their predictions of the spectra do not include free parameters,therefore provide valuable points of reference in the Casten triangle.In nuclear physics,the one-dimensional version of the purely AOPsαHare X(5)-β2αand E(5)-β2αmodels.One might ask:are there other flexible potentials that are able to provide us with the properties ofαH,depending on a very limited number of parameters and are characterized by the presence of barriers in its structure? Of course,these potentials will allow us to model various deformation related features such as critical points,coexistence phenomena,fluctuations phenomena,and QSPT,which appear in the complex dynamics of many nuclei,particularly,quadrupole–octupole shape deformations nuclei.

First,we will consider the DLPs which are chosen to be of the following form:

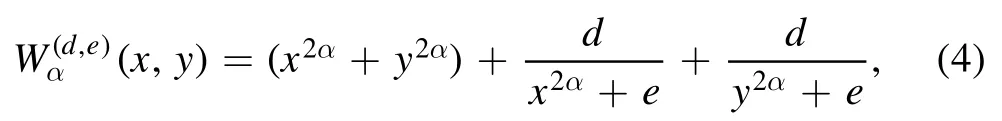
where d and e are free parameters and α=2,3,….These potentials can be approached to purely AOPs,αH,and,at the same time,are characterized by the existence of barriers.The shape of the potential depends on the values ofdande,see fgiure 1.The DLPs(x,y)are symmetric about thex-andy-axis,with a core at the center,(x,y) =(0 ,0) .The evolution of the vertical cross-sections of the DLPs (4) with regard to the parameterdis shown in fgiure 1(b).The frist part ofisHαand the second part produces the barrier.Both the barrier height and thickness increase with the increase ofd,but decrease wheneincrease.The curvature of the minima is more spherical than the minima of the AOPsWe restrict our attention to the regionR={(d,e):d,e∈[0 .1,1] },where the DLPs (4)evolve from four minima (as in figure 1(c)) to the near flat case,αH,(shown in figure 1(d)).

Figure 1.(a)The three-dimensional representation of the DLPs (b)The vertical cross-sections of the DLPs (c)and(d)are the two-dimensional representation of the potentialsandrespectively(contour plots).The potential changes from four minima potential to approximately flat minimum potential,H2.(For interpretation of the colors in the figure(s),the reader is referred to the web version of this article.)

We are now able to investigate the evolution of the spectra of the DLPsas a function of the parametersdande.It is sufficient and valuable to survey this behavior at the four boundaries ofR.The energy spectra of the DLPs,and0.1 ≤e≤1 andα= 2 are presented in fgiures 2(a)and(b),respectively.The energy spectrum shows a transition from the spectrum of the TSM to theαHsolution,figure 2(b).The TSM is achieved for small values ofe,where the DLP forms wide spherical minima separated by high barriers.The other limit occurs for high values ofe,where theH2term is dominant.It is important to stress that we obtained here the TSM from large spherical minima separated by high barriers.However,for the AOPsorthis mode is generated from very narrow deformed minima separated by high barriers.Obviously,the DLPsand the AOPsorare in two sides of ISWP.Similarly,we can study the evolution of the spectra on the other two boundaries ofR.The energy spectra of the DLPs,and0.1 ≤d≤1,are presented in fgiures 2(c)and(d),respectively.These potentials have the fourfold TSM for high values ofd,but the energy spectra,for small values ofd,can be considered very close to the spectra of theαH,figure 2(c).

A better understanding of such models is fulfilled by investigating the probability density,∣ Ψ(x,y)∣2.The development of the ground state and first excited state wave functions of the DLPsas a function ofe,is represented in figure 3.Beginning frome= 0.05,the ground state wave function is composed of four separate peaks.Ate= 0.1,the four peaks of probability density become closely spaced and begin to combine and join together.Ate= 0.2,the probability density forms an isolated island with four peaks.Ate=0.3,the crest of probability density is approximately flat and squared in the shape.When the ground state becomes above the barrier,ate=1,we have a normal single-peak probability density for the ground state.In the same manner,ate= 0.05,the first excited state wave function is composed of two separate peaks and two separate troughs.By increasing the value ofe,the four peaks of the probability density,with unequal height,become closely spaced.At a specific point,the probability density of the first excited state wave function is composed of two pieces.When the first excited state is near the top of the barrier,each piece of probability density is delocalized and more extended over the corresponding two minima and has two unequal peaks,one peak around the first minimum,however,the second peak spreads to the otherminimum.Ate= 1,we have normal two peaks probability density,with equally high,figure 3.

Figure 2.Representation of the first nine energy levels,as a function of d ande for DLPs (normalized to the ground state energy).(a) and (b) show the behavior of the spectra of the DLPs against the parametere with d =0.1 and 1,respectively.However,(c) and (d) display the energy spectra of the potential against the parameter d with e =0.1 and 1,respectively.

These results show the capability of the DLPs,which are characterized by wide spherical minima separated by high barriers,to approachH2.As expected,the results,particularly the behavior of the wave functions,are similar to those for the AOPsor[13] because the parameters are in the regionR,where the DLPs (4) evolve from four minima to the near flat case,however,in this case,the potentials are on the other side of ISWP.

Additionally,with barrier structure,the following potentials can be approached to HOP

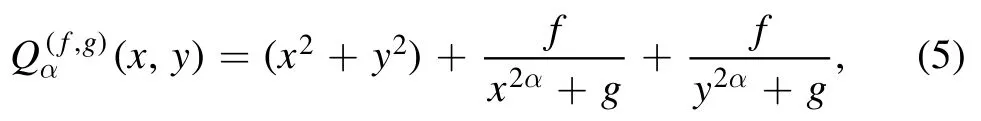
wherefandgare free parameters andα=2,3,… .The shape-changing of the vertical cross-sections of the DLPs (5)is shown in figure 4(b),as a function off.The first part of the DLPs(5)is the HOP and the second part produces the barrier.The height and thickness of the barrier increase with the increase off,but decrease with the increase ofg.The curvature of the potential is completely inside the HOP.Again,we focus on the regionR={(f,g) ,f,g∈[0 .1,1] },see figures 4(c) and (d).

The energy spectra of the DLPsand0.1 ≤f≤1,0.1 ≤g≤1 andα= 2,presented in figure 5,show a transition from the spectrum of the HOP solution to the TSM.However,this transition is totally different from theandcases.The upper level withn= 3,from the first quartet of levels,and the lower levels withn= 4,5,from the second quartet of levels,evolve such that they form the three-fold degenerate level of HOP,figures 5(b) and (c).Similarly,the upper levelsn=6,7,from the second quartet,and the lower leveln=8,from the third quartet,are a portion from the four-fold degenerate level of HOP.Actually,the potentialsandevolve from four minima potentials to the near flat case,αHor ISWP while the DLPsevolve from four minima potentials to HOP.

As a result,we can always reproduce the properties of the independent-parameters potentials,HOP,ISWP,orαH,using potentials characterized by the existence of barriers.These potentials are very convenient to describe QSPT because,according to their parameters,they can possess one minimum,a flat shape,or four minima separated by barriers.

Now,we are in a good position to study the coexistence phenomena with the DLPs.The third class of the DLPs is of the form

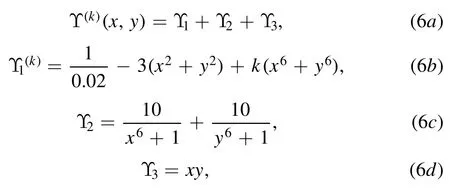
Figure 3.The contour plots of the DLPs (left panel),the ground state probability density (medial panel),and the probability density of frist excited state (right panel),as e =0.05,0.2,0.3,and1 from top to bottom,obtained numerically.

wherekis a free parameter.The DLPs Υ(k)consists of three parts.The first part,Υ1,generates symmetric four minima potential,the second part,Υ2,produces the barrier and the third part,Υ3,destroys the symmetry of the potential.The function,Υ,builds asymmetric four minima potential,see the frist column of fgiure 6.In other words,we have two symmetric twodimensional double-minimum potentials with unequal heights.For each potential,the two minima are mirror images of each other and locatedat for the fristpotential and atfor the second one.

For asymmetric potential,the energy levels do not occur in quartets,and,except in a case of accidental degeneracy,the energies in one potential are different from those in the other.We have two configurations in the same system.The eigenfunctions near the bottom are localized in their respective wells(except when the barrier is low),but the wavefunctions close to the top of the barrier may extend through the classically forbidden region into the other wells.Conversely,for each symmetric two-dimensional double-minimum potential,the energy levels of both wells occur in pairs and have the same values.The eigenfunctions are delocalized,extending over both wells.

When two (or more) types of spectra associated with different configurations coexist in the same energy region,we call them coexistence phenomena.This circumstance occurs when configuration mixing due to tunneling is weak and the wave functions retain their localizations about different minima.In contrast,when the configuration mixing is strong,a largeamplitude configuration fluctuations(delocalization of the wave functions) extending to different local minima may occur.

For the ground state of the first and second configurations of the potentialΥ,the evolution of the probability density as a function of the variablesxandyand the parameterkis represented in figure 6.Atk= 0.05,the probability density of the first configuration is composed of two separate peaks.By increasing the value ofk,the two peaks of the probability density become closely spaced.Atk∈[2 .2,2.4] ,the probability density is composed of two pieces.When the state is in nearness to the top of the barrier,the tunneling is strong and the fluctuations phenomena take place,each piece of probability density becomes more extended over two minima and has a peak around the one minimum,however,its tail spreads to the other one.When the state is above the barrier,one obtains normal two peaks probability density with equal height,as presented in figure 6 (right panel).

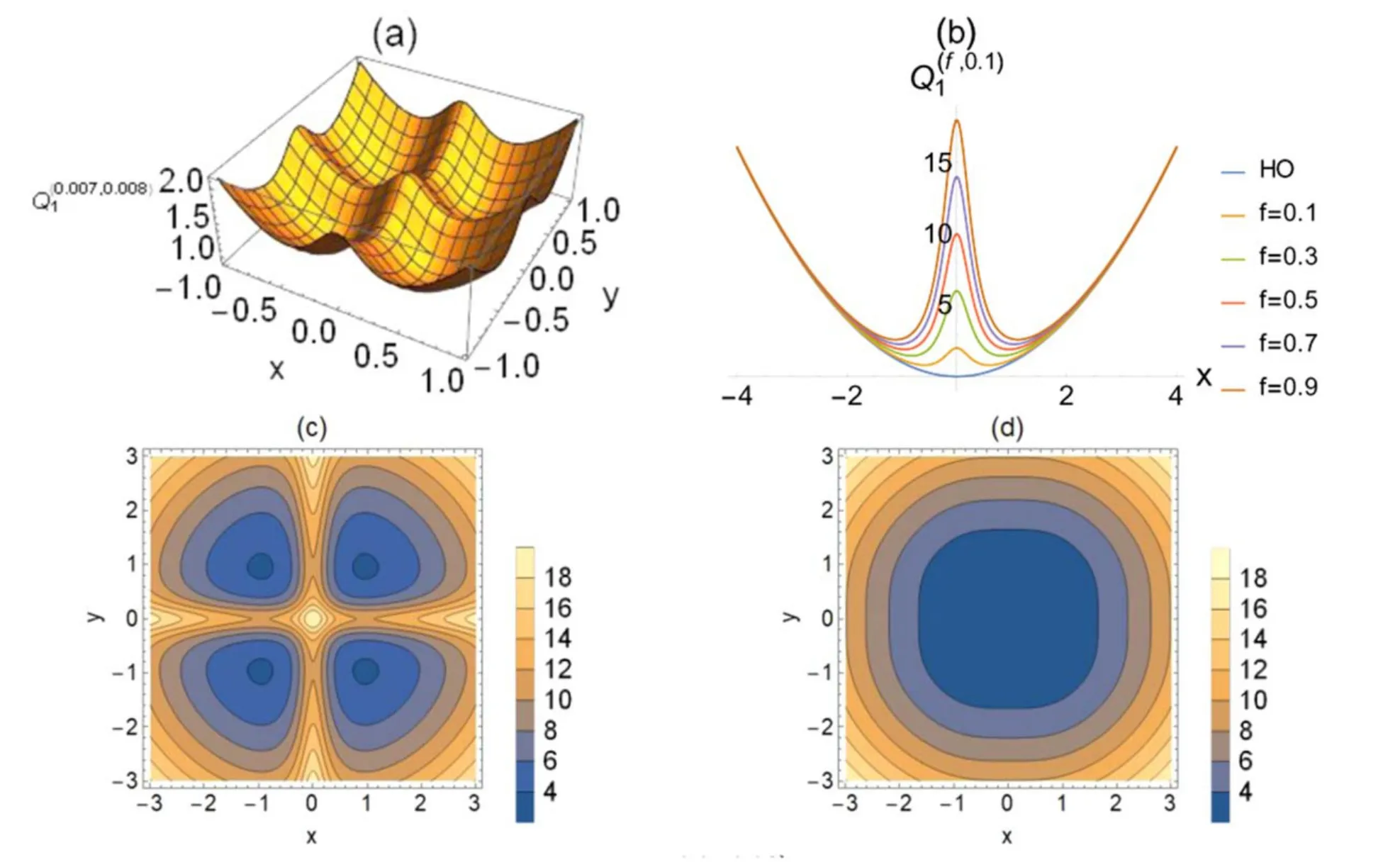
Figure 4.(a) The three-dimensional representation of the DLPs (b) The vertical cross-sections of the DLPs (c) and (d) are the contour plots of the potentials and respectively.The potential changes from four minima potential to HOP, H1.

Figure 5.Representation of the first nine energy levels,as a function of f and g for DLPs (normalized to the ground state energy).(a) and (b) show the behavior of the spectra of the DLPs against the parameter g with f =0.1 and 1,respectively.However,(c) and (d) display the spectra of the potential against the parameter f with g =0.1 and 1,respectively.

Figure 6.The contour plots of the potentials (left panel),the ground state probability density of the second configuration(medial panel),and the ground state probability density of the first configuration (right panel),as k =0.05,2.2,3,and 10 from top to bottom,obtained numerically.

Beginning fromk= 0.05,the ground state probability density of the second configuration is composed of two separate peaks.With a decrease in the barrier height,the two separate peaks of the probability density become closely spaced.At a certain point,the ground state probability density forms an isolated island with the four unequal peaks that happens as a consequence of the strong tunneling between the potential wells.In this case,one says that two configurations coexist in the same system as well as in the same state.When the ground state of the second configuration is above the barrier,we have a single-peak probability density,as represented in figure 6 (medial panel).Depending on what was previously mentioned,with changing ofk,a transition is covered from coexistence phenomena of the two distinct TSMs to fluctuations phenomena with unequal peaks ending with the spectra ofαH.

3.Non-CQOM

The nucleus is a quantum many-body system so that its shape is depending on the number of nucleons that exist in the nucleus and the nature of the interactions between the nucleons.For example,doubly magic nuclei,in their ground state,have a spherical shape.If this nuclear system is excited,or if more nucleons are added or subtracted,the spherical symmetry is distorted and the nucleus turns into a deformed shape (prolate or oblate).A major part of deformed nuclei exhibit quadrupole reflection-symmetric shapes,and their spectra are characterized by positive-parity bands.While,octupole reflection-asymmetric shapes(pear-like nuclei)exist in certain regions [14–20],either in an octupole deformation or octupole vibrations.Around neutron (proton) numbers,namelyN(Z) =34,56,88,and 134,the tendency towards octupolarity becomes stronger.The Rn isotopes,with A=218–222,are the best examples of the octupole vibrators.However,the222,224,226,228Ra and224,226,228,230Th isotopes are typical octupole deformation.

Figure 7.(a) The three-dimensional plot of the potential W (β2,β3,0) .(b) The evolution of the vertical cross-sections of the potentials W (β2,β3,I),at β3 = 0,as a function of the angular momentum I and β2.

Most studies of first- and second-order QSPT have paid more attention to quadrupole degrees of freedom,either for axially-symmetric deformed shapes or triaxial shapes.Much less analysis are the QSPTs connected to reflection-asymmetric shapes.Geometric collective models [28–31],algebraic models[32],and microscopic energy density functionals[33–36] have been used in studies of this type of QSPT.In[37,38],the QSPT from octupole vibrations into octupole deformation has been considered.Additionally,the double QSPT was reported[39],between non-octupole and octupoledeformed shapes and simultaneously between spherical and quadrupole-deformed prolate shapes.A different critical point including quadrupole and octupole deformations have been suggested [28–31] expanding the idea of critical point introduced for studying positive parity states.

In the CQOM,the even–even nucleus can able to oscillate with respect to the quadrupoleβ2and octupoleβ3variables.The Hamiltonian of the CQOM can be written as

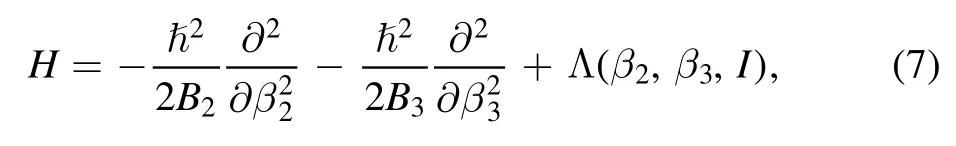
Where

withX(I) = [d0+I(I+1) ]/2.HereB2(B3),C21(C31) andd2(d3) are quadrupole (octupole) mass,stiffness,and inertia parameters,respectively,whiled0determines the potential core atI=0.The two-dimensional potential (8) does not contain theγdegree of freedom.The potential function Λ consists of two parts.The frist part,generates HOP however the second part,produces an angular momentum dependent core.If(β2,min,β3,min)denotes the position of the bottom of the potential (8) such thatβ2,min≠0andβ2,min≠0,the model parameters satisfy the following relation,d2/C21=d3/C31.In this situation,the shape of the bottom of the potential is an ellipse.If we consider the prolate quadrupole deformationβ2＞0,the system oscillate betweenβ3＞0andβ3＜0along the ellipse surrounding the infniite potential core.It should be noted that,in the coherent approach,the model is limited to a specifci category of exact analytic solutions.On the contrary,in the non-coherent case,the parameters are all allowed to vary without any constraint.

From the results of section 2,we realized that the potentials (4) and (5) are constructing bridges between the HOP and the purely AOPs,αH.Furthermore,by changing the barrier height,we can have examples of the occurrence of fluctuations phenomena in the ground state and excited states.These essential ideas must be applied to the CQOM.It is fundamental to know how stable octupole deformation is,i.e.we need to know the size of fluctuations around the equilibrium value ofβ.3Moreover,in [40–42],the analysis of the octupole correlations was based on a simple one-dimensional model of octupole collective motion.The potential of this model has two minima,symmetric aroundβ3= 0and frozen quadrupole variable was considered.Depending on the height of the inner barrier between a reflection asymmetric shape and its mirror image a parity splitting arises.In such a way the explicit form of the potential in terms of the quadrupoleβ2and octupoleβ3deformation variables was not given.As a consequence,some basic characteristics of the quadrupole and octupole modes and their interaction remain outside of consideration such as the behavior of the system in dependence on the quadrupole and octupole stiffness.On the other hand,in CQOM[26,27],the potential of the system depends on the two deformation variablesβ2andβ3.The system is considered to oscillate between positive and negativeβ3values by rounding an infinite potential core in the (β2,β3)plane withβ2＞0.In this case,there is no barrier that sepratesβ3＞0andβ3＜0after the quadrupole coordinateβ2is let to vary.Hence,there is a need to suggest new potentials that have the advantages of the HOP and that generate a barrier separatesβ3＞0andβ3＜0along theβ2axis.The strength of barrier penetration controls the amount of shift in the energy of a negative-parity state with respect to the positive-parity one.

Here,we focus on the fluctuations phenomena through the barrier atβ3= 0in the space (β2,β3) and examine the evolution of the potential in dependence on both quadrupole and octupole degrees of freedom as well as on the collectiveangular momentum.To this end,we introduce the following effective potentials,using DLPs(4)and(5)in the quadrupoleβ2and octupoleβ3axial deformation variables

Table 1.Theoretical and experimental energy spectra of 100Mo[43]and 146Nd[44],normalized to the energy of the first excited 2+state.For each nucleus,the theoretical spectraandare the results from the potentials(8),(9a),and(9b),respectively.The brackets are used if the spin assignments are uncertain.

Table 1.Theoretical and experimental energy spectra of 100Mo[43]and 146Nd[44],normalized to the energy of the first excited 2+state.For each nucleus,the theoretical spectraandare the results from the potentials(8),(9a),and(9b),respectively.The brackets are used if the spin assignments are uncertain.

100Mo 146Nd+L∊i exp ∊iQ∊iW Λ∊i∊iexp ∊iQ∊iW Λ∊i Yrast +0 0 0 0 00 0 0 0+2 1 1 1 1 1 1 1 1+4 2.121 27 2.262 17 2.211 52 2.322 41 2.298 81 2.440 77 2.246 87 2.416 71+6 3.448 66 3.569 56 3.572 88 3.707 91 3.922 43 3.991 42 3.642 52 3.931 76+8 4.905 15 4.889 92 5.056 45 5.112 75 5.715 07 5.579 33 5.158 55 5.479 37+10 (6.285 85) (6.216 31) (6.644 81) (6.526 41) 7.315 34 7.183 33 6.777 89 7.041 51+12 (7.584 39) (7.545 76) (8.325 69) (7.944 75) 8.800 57 8.796 12 8.488 65 8.611 64+14 (9.101 38) (8.876 95) (10.0899) (9.365 87) 10.3442 10.4142 10.2820 10.1867+16 12.0328 12.0355 12.1508 11.7653 Yrast −1−3 3.562 92 1.6204 1.584 62 1.647 13 2.621 42 1.697 97 1.602 24 1.687 77−5 (4.368 55) (2.913 45) (2.875 53) (3.011 49) 3.3442 3.208 84 2.928 27 3.167 98−7 (5.308 44) (4.228 70) (4.300 64) (4.408 82) 4.472 01 4.782 61 4.386 72 4.703 08−9 (6.159 82) (5.552 60) (5.838 39) (5.818 81) 5.963 42 6.379 91 5.956 14 6.259 15−11 (7.529 31) (6.880 75) (7.474 31) (7.235 14) 7.714 19 7.988 90 7.622 45 7.825 82−13 (9.222 93) (8.211 19) (9.197 88) (8.655 04) 9.464 52 9.604 62 9.375 46 9.398 68−15 11.1457 11.2245 11.2073 10.9756 Non-yrast +2 1.297 80 1.183 20 0.680 92 2.212 67 2.017 19 1.445 47 0.686 05 2.458 43+4 2.733 20 1.609 49 1.146 30 2.625 27 2.871 75 2.444 63 1.686 05 3.457 11+6 (3.307 32) (2.182 94) (1.680 92) (3.211 91) 3.845 75 3.886 04 2.932 92 4.874 89/ħ B 2 2 2 2.000 00 12.0000 1.500 00 0.900 00 7.000 00 1.000 00 Δ 0.779 32 0.835 37 0.708 31 0.463 95 0.628 83 0.542 15

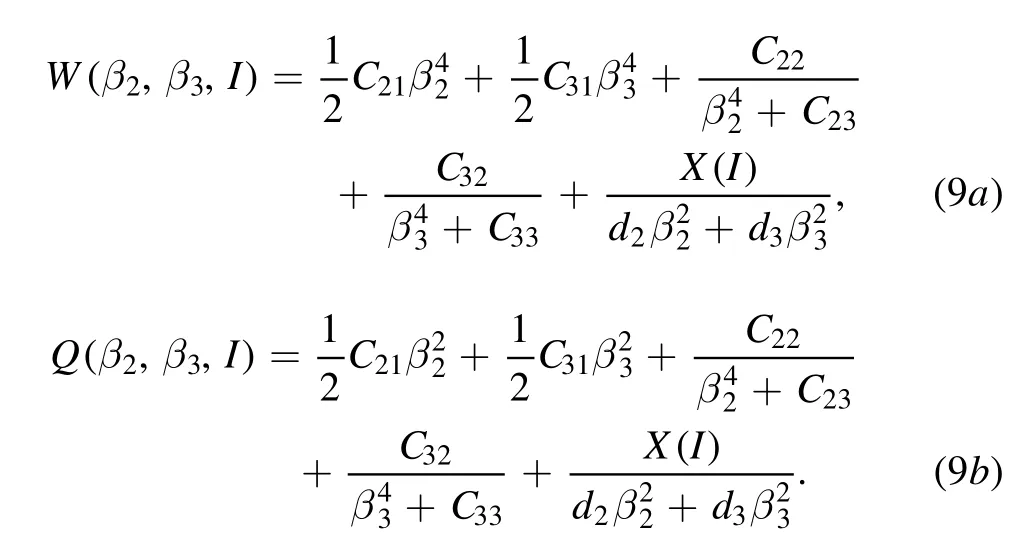
The shape ofW(β2,β3,I)is illustrated in figure 7(a).It is characterized by two energy minima forβ3＜0andβ3＞0 separated by a barrier.With increasing angular momentum,centrifugal forces modify the effective potential.This potential,thus,depends on the angular momentum.Atβ3= 0,the height of the barrier,betweenβ3＜0andβ3＞0,depends onβ2.The evolution of the vertical cross-sections of the potential(9a)as a function of the angular momentum andβ2variable is shown in figure 7(b),atβ3= 0.

The model formalism with potentials (8) and (9) was applied to several nuclei,namely,100Mo,146,148Nd,148,150Sm,220Ra,220,222Rn,and220,222Th.All selected nuclei are characterized by the energy ratioin the range 2–2.5,the energy ratioin the range 2–3.5,and the energy bands with alternating parity.From tables 1–5,good agreement has been found between the calculated and measured spectra.

The energy levels are determined by (7) and potentials(8) and (9).The two-dimensional Schrödinger equation is solved for each value ofI= 0,1,2,… separately.The energy spectrum is normalized tostate of the ground state band such that

The root mean absolute error is defined as,Δ=whereandare the experimental and calculated energies of the ith level andnlrepresents the number of levels.Δ is one of the important statistical quantities which is used for the validation of the predicted result.Once the diagonalizations,using the finite-difference method,have been accomplished for all angular momenta,one gets a spectrum and can determine the value of Δ.Then the parametersC2i,C3i,d2,d3,d0,i=1,2,3 and the boundaries parametersβ2bandβ3bof the finite-difference method can be adjusted to give the best description of experimental energies.

By following this procedure,we can have the best fitting of experimental data of an individual nucleus.However,we choose to go a step further and search for the global parametrization(maximum common parameters of a set of nuclei with a minimum value of Δ).As an alternative approach,we searched for a simplified global CQOM parametrization for selected octupole nuclei that belong to different regions in the nuclear landscape.

Table 2.The same as in table 1,but for 148Nd [46] and 148Sm [46].

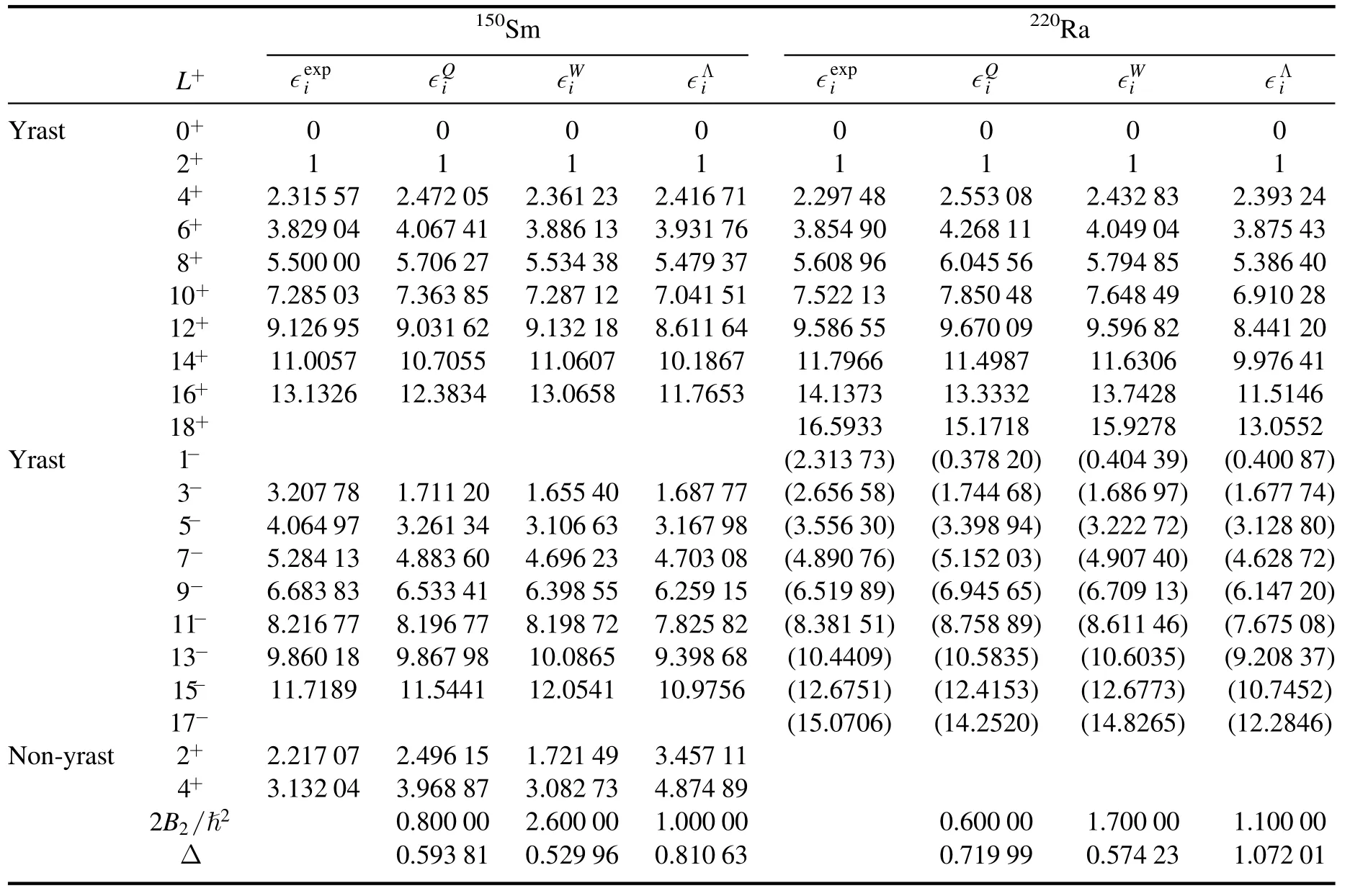
Table 3.The same as in table 1,but for 150Sm [47] and 220Ra [48].

Table 4.The same as in table 1,but for 220Rn [48] and 220Th [48].

Table 5.The same as in table 1,but for 222Rn [49] and 222Th [49].

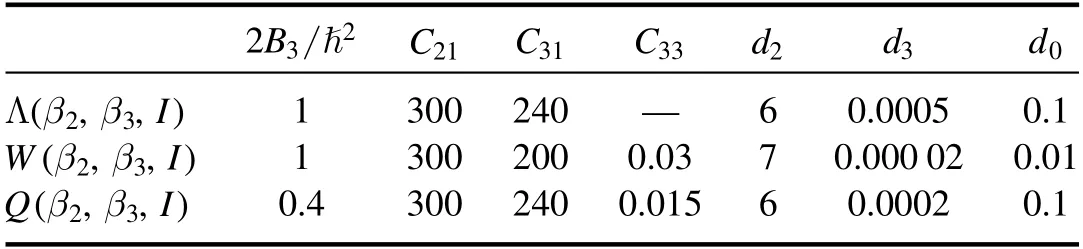
Table 6.The parameters of the potentials Λ(β2,β3,I),W (β2,β3,I )and Q (β2,β3,I )are B3, d2 ,and d3(in ħ2 MeV−1),d0 (in ħ2),C21 andC31(in MeV),C2 2 =C32=1 MeV,whereasC23 andC33 are dimensionless,C2 3=1.

This set of global parameters leads to a description of about 200 collective levels in 10 nuclei with a root mean absolute error from the observed level energies less than 0.7.In this approach,all the model parameters are constants exceptB2.For the best ftiting of experimental data,the value ofB2must be adjusted.The values of the global CQOM parameters of the potentials(8)and(9)are tabulated in table 6.The idea of global parametrization is not new.This technique was applied to many isotope series in the study of exotic nuclei [45].

Atβ3= 0,for a small value of quadrupoleβ2variable,the height of the barrier is very high.With increasingβ2,the height decreases.At some point,it reaches its minimum value.Increasing further theβ2variable,the height of the barrier is increasing again.This geometric analysis suggests that the oscillations of the system in the two-dimensional case of simultaneous manifestations of the quadrupole and octupole modes are performed in a different way,compared to the one-dimensional case of a reflection asymmetric shape with a frozen quadrupole variable.The presence of a tunneling effect in the space of the octupole variableβ3is sensitive to the quadrupoleβ2variable.Straightforwardly,in the (β2,β3)space,the strength of the tunneling through the barrier of each wave function varies with quadrupoleβ2variable.As a result,the parity shift effect observed in nuclear alternating parity bands,which can be explained as a result of the tunneling through the barrier,depends on the height of the barrier.Thus,not only the shape of wave function but also the energy spectrum are sensitive to the height of the barrier.

The comments on the model results are as follows:

The spectra of ten even–even nuclei characterized by yrast and non-yrast energy sequences with alternating parity and the energy ratioin the range 2–2.5 are discussed within the framework of CQOM.A satisfactory degree of agreement is obvious between the calculated energy spectra and the corresponding experimental values.In general,the results of HOP with barriers in its structure(9b)suggest more exact outcomes,i.e.minimum Δ values,in comparison with the pure HOP predictions.

As seen in figure 8 and tables 1–5 the odd–even staggering is significant only for the lowest three odd levels,the positive-parity states (even levels) are extremely well reproduced,as well as the rest of the negative-parity states (odd ones).From figure 8,we can understand why global parametrization was able to generate the spectra of nuclei from different regions.These spectra are very close and look like lines with different slopes and starting from one point.

These results are in agreement with the findings of research [29].In this work,an analytic,parameter-free solution of the Bohr Hamiltonian involving axially symmetric quadrupole and octupole deformations,as well as an infinite well potential,was obtained.This is done after separating variables in a way reminiscent of the variable moment of inertia concept.They find that the positive-parity states are extremely well-reproduced as well as the negative-parity states with the exception of the first three negative-parity levels.A similar phenomenon exists in the interacting boson model.In [50,51],the level energy spectra of a set of 26 nuclei presenting a vibrational structure were analyzed using a simple U(5) prescription in the interacting boson model.It was observed that theenergies are quite generally about 15% lower than expected from the global nuclear properties.The origin of this observed phenomenon is not clear.One hypothesis would be that some interactions not included in the standard interacting boson model have to be considered.In our case,a more complete investigation,including also more nuclei,should be performed to test the reality of such interaction which would be expected to depend on angular momenta and parity of the levels.It also decreases with the increase of the angular momenta of negative parity levels.

For most nuclei considered here,the yrast positive- and negative-parity states belong to a single band,that is,the two bands are located close in energy which is the hallmark of octupole deformation.In this case,the existence of the barrier betweenβ3＜0andβ3＞0is essential in the description of octupole deformation nuclei.This explains why the potential(9b) suggests more exact outcomes.

The oscillations of the system in the two-dimensional case of the simultaneous manifestation of the quadrupole and octupole modes are performed in a different way,compared tothe one-dimensional case of a reflection asymmetric shape with a frozen quadrupole variable.The height of the barrier of the potentials (9a) and (9b) changes with quadrupoleβ2variable which controls the shape of the wave function.For the small value of quadrupoleβ2variable,the height of the barrier is very high,there is no tunneling through the barrier.With increasingβ2,the height decreases and one can have cases of the fluctuations phenomena in the wave function.The wave function extends over the two minima and has two peaks around the two minima,as well as the corresponding probability density.Increasing further theβ2variable,the height of the barrier is increasing again.

Figure 8.Experimental energy ratios for states of the positive-parity ground state band (I even) and the lowest negativeparity band (I odd),as functions of the angular momentum I,for 100Mo [43],146Nd [44],148Nd [46],148Sm [46],150Sm [47],220Ra[48],220Rn [48],220Th [48],222Rn [49] and 222Th [49].

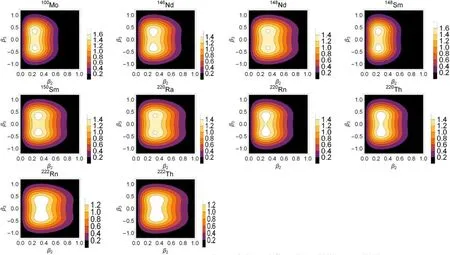
Figure 9.The contour plots of the ground state wave functions of 100Mo,146,148Nd,148,150Sm,220Ra,220,222Rn,and 220,222Th using the potential (9b).

In this case,there is no tunneling through the barrier.Figure 9 represents the ground state wave function of the nuclei considered in this work,using the potential (9b).The peaks of the wave function begin to merge,however still distinguishable,for100Mo,146,148Nd,and148,150Sm.For220Ra,220,222Rn,and220,222Th,the ground state wave function posses a broader peak engulfing both wells of the associated effective potential.

The correspondence between the ground state bands of the current scheme,using(9a),and X(5)-β4model are indeed so close because the two models are derived from the collective Bohr–Mottelson Hamiltonian and employ quarticβ4potential.Besides,the quadrupole degree of freedom,that associated with the two models,is expected to play an essential role in the description of the properties of the ground-state band.Obviously,the potential (9a) can be viewed as an extension of X(5)-β4model [6],where the octupole degree of freedom is considered for the sake of the negative parity bands,and at the same time theγdegree of freedom is ignored to make the problem more tractable.

4.Conclusions

The nine-point finite difference method is used for the diagonalization of the Hamiltonian with DLPs.These potentials can evolve from wide spherical minima separated by high barriers to the near flat case or HOP.The spectra of DLPs(4)and (5) show a transition from TSM to the spectra of purely AOPs or HOP,and concurrently present many new features,such as the coexistence phenomena and fluctuations phenomena in the ground state and excited states.We had a ground state wave function with a four-peak structure.It is essential to distinguish between two types of potentials.For asymmetric potential,two or more configurations coexisted in the same system as well as in the same state and the fluctuations phenomena are characterized by the existence of peaks with unequal heights in the same wave function.In contrast,for symmetric potential,one configuration existed,the eigenfunctions were delocalized and the fluctuations phenomena were characterized by the existence of peaks with equal heights in the same wave function.Using these potentials,we shift the analysis of the coexistence phenomena and fluctuations phenomena from one that focuses on ISWP to one that focuses on HOP and purely AOPs.

Furthermore,by using DLPs in a CQOM Hamiltonian,we provide a global description of yrast and non-yrast bands with alternating parity in a set of even–even nuclei,namely,100Mo,146,148Nd,148,150Sm,220Ra,220,222Rn,and220,222Th.The global CQOM parametrization for selected octupole nuclei is achieved.We also obtained a ground state wave function with a two-peak structure.It is important to point out that,and this is the central focus of the present work,the existence of the barrier betweenβ3＜0andβ3＞0plays the central role in the study of the quadrupole–octupole deformed nuclei.The wave function shape is a reflection of the shape of the potential.

ORCID iDs