Bäcklund transformation,infinite number of conservation laws and fission properties of an integro-differential model for ocean internal solitary waves

Di Yu,Zong-Guo Zhang,Huan-He Dong and Hong-Wei Yang,*

1 College of Mathematics and System Science,Shandong University of Science and Technology,Qingdao 266590,China

2 School of Mathematics and Statistics,Qilu University of Technology (Shandong Academy of Sciences),Jinan,250353,China

Abstract This paper presents an analytical investigation of the propagation of internal solitary waves in the ocean of finite depth.Using the multi-scale analysis and reduced perturbation methods,the integrodifferential equation is derived,which is called the intermediate long wave(ILW)equation and can describe the amplitude of internal solitary waves.It can reduce to the Benjamin–Ono equation in the deep-water limit,and to the KdV equation in the shallow-water limit.Little attention has been paid to the features of integro-differential equations,especially for their conservation laws.Here,based on Hirota bilinear method,Bäcklund transformations in bilinear form of ILW equation are derived and infinite number of conservation laws are given.Finally,we analyze the fission phenomenon of internal solitary waves theoretically and verify it through numerical simulation.All of these have potential value for the further research on ocean internal solitary waves.

Keywords: infinite conservation laws,the integro-differential equation,internal solitary waves,fission properties of waves

1.Introduction

Internal solitary waves are a very common hydrodynamic phenomenon that occurs in the ocean.Internal solitary waves are generated by fission during the propagation of the internal waves.The characteristic wavelength of internal solitary waves ranges from several hundred meters to several thousand kilometers and contain huge energy.Due to its enormous energy and induced strong shear flow,Internal solitary waves may be a severe threat to marine engineering structures,such as platforms and marine risers [1,2].Therefore,the study of internal solitary waves is of great significance.

Nonlinear partial differential equations have been more and more widely used in various disciplines,such as biology,physics,ecology,etc[3–5].The intermediate long wave(ILW)equation is an important integro-differential equation,which describes the propagation of long internal gravity waves in a stratified medium of finite depth[6,7].Kubota et al[7]derived the ILW equation in 1978 and obtained the four conserved quantities.Later,Zhou[20](1985),Tutiya[21](2003),Guo[8](2018)and others also made further research on ILW equation.ILW equation also appears in other circumstances,for instance in the oceans and in the atmosphere.It can reduce to the Benjamin–Ono equation in the deep-water limit,and to the KdV equation in the shallow-water limit [6–8].In this paper,we will derive the ILW equation by using the multi-scale analysis and perturbation methods[9,10]to describe the internal solitary waves in the ocean of finite depth.

Conservation laws play an important role in mathematics and physics.Naturally,how to construct conservation laws has also become a research hotspot[11–13].Over the past few decades,a great deal of work has been done on infinite number of conservation laws [12–15].However,in previous studies,people have paid more attention to the conservation laws of nonlinear differential equations[11–14],but little attention has been paid to nonlinear integro-differential equations.In this paper,we derive the Bäcklund transformation in bilinear form [16–18] and study infinite number of conservation laws of ILW equation.

In this paper,we derive the ILW equation by using the multi-scale analysis and perturbation methods.And then,the bilinear form and multi-soliton solutions of the model are obtained according to the Hirota bilinear method.Next,we derive the Bäcklund transformation in bilinear form and infinite number of conservation laws.Finally,we analyze the fission phenomenon of internal solitary waves theoretically and verify it through numerical simulation.

2.Derivation procedure of model

Here,we consider the two-dimensional motion of two layers of incompressible and finite-depth fluids stratified by density in the y direction.The governing equations are as follows:

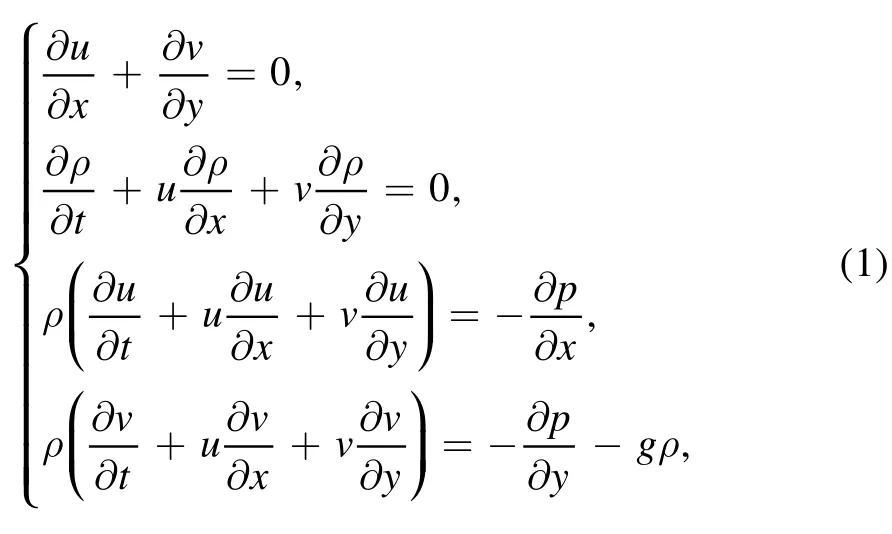
where u and v are velocity components in the directions of x and y,ρ is the density,t is the time variable,p is the fluid pressure,and g is the acceleration of gravity.Equation(1)has a solution that represents a motionless ground state:u=u0=0,v=v0=0,p=p0(y),ρ=ρ0(y),and the basic hydrostatic balance isAppropriate boundary condition associated with v(y) is v=0,at y=0 and y=h1.

We assume that the density is continuous at y=h0.At 0 ≤y ＜h0,the density changes with y.At h0≤y ≤h1,the density is constant:

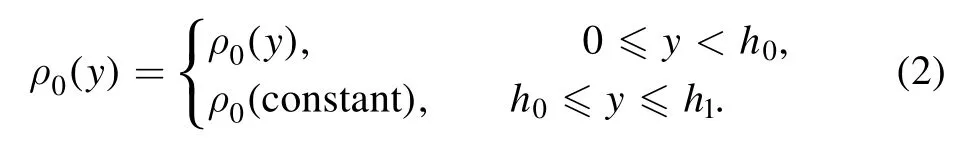
Next,we study the wave equation by matching the upper and lower solutions at y=h0with the coordinate transformation and perturbation methods.

2.1.In the domain 0 ≤y ＜h0

In the domain 0 ≤y ＜h0,we introduce the small parameter ∊,which represents the nonlinear strength.Then,we introduce the Gardner and Morikawa type transformations as follows [19]

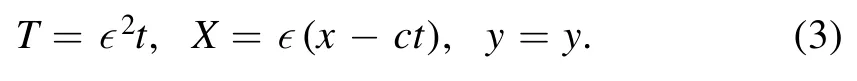
In addition,the following variables representing the excited state are expanded to the power of ∊:

Substituting equations(3)and(4)into(1),the lowest order approximate equations of ∊can be obtained

Eliminating p1,u1and ρ1,we can obtain the governing equation of v1

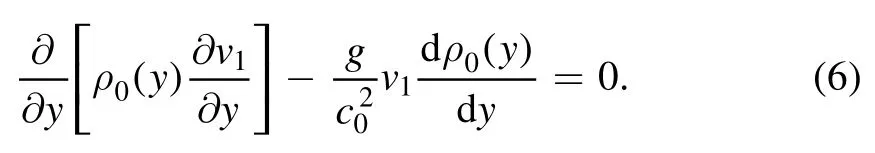
By separating variables,we assume that the solution of equation (6) has the following form

Substituting equation (7) into (5),it is easy to find that

Further,we can obtain the next order approximate equation for ∊

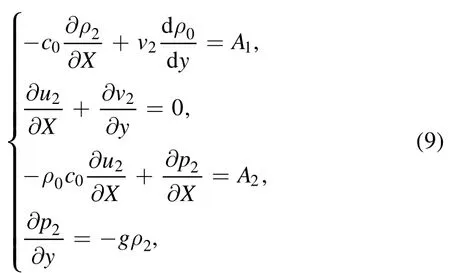
where

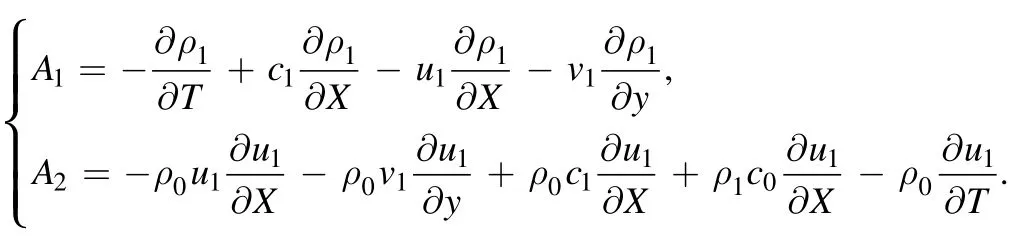
Similarly,eliminating p2,u2and ρ2,the governing equation of v2is as follows:

Multiply both sides of equation (10) by φ,and integrate y from 0 to h0,we can get

2.2.In the domain h0 ≤y ≤h1

Similarly,in the domain h0≤y ≤h1,introduce the following transformations:

Suppose that u,v,c,p and ρ have the following asymptotic expansion:

Substituting equations (12) and (13) into (1),we can obtain

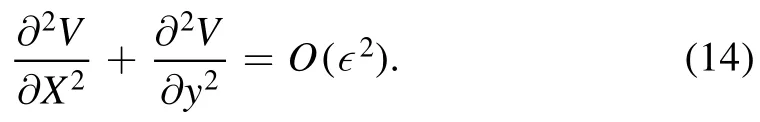
According to Fourier transformation,Fourier inverse transformation and the convolution theorem [20],we can get the solution of equation equation (14) in the following form

2.3.Matching at y=h0

Now we can match the solutions of the two regions at y=h0.Assuming that the solutions of the two regions are continuous at y=h0,we can obtain

Compare the coefficients of the same power of ∊in the first equation in equation (17),it is easy to find that

Based on equations (16) and (19),we can obtain

Then,we can get from equations (18) and (20)

Next,substituting equations (19) and (21) into (11),the new governing equation is obtained

where

Equation (22) is a model which is used for the first time to describe internal solitary waves in the ocean.When a1=0,it can be found in Kubota(1978)[7].Here it should be noted that when h1→∞,equation (22) is converted to the BO equation; in the opposite limit,equation (22) is converted to the KdV equation.

3.Bilinear form and multi-soliton solutions

In this section,we shall seek the bilinear form and multisoliton solutions of equation (22) by the Hirota bilinear method.Assuming that the solution is real and finite for all X,T,the form of the solution is as follows

where

and satisfies the boundary condition f →0,|X|→∞,g can be written in the form

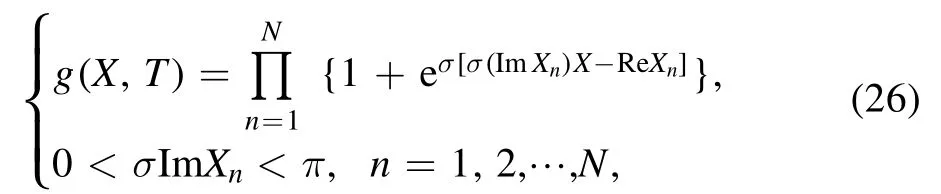
where Xn(n=1,2,…,N) are complex functions of T,g+is the complex conjugate of g−.Use the following formula

we can obtain

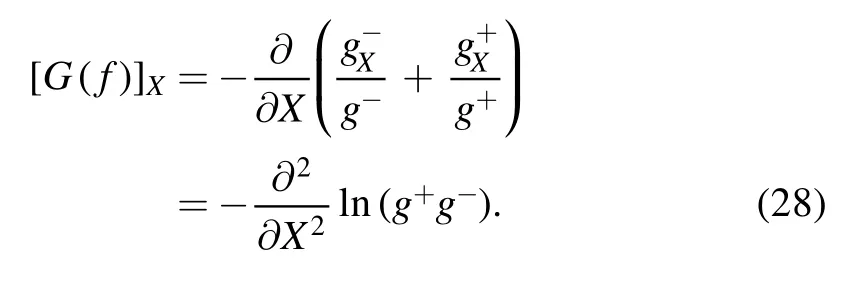
From equations(24)and(28),without loss of generality,let a2=2a3,we can obtain the bilinear equation as follows

For the one-soliton case,it may be confirmed by direct substitution that

Substituting equation (30) into (23),the one-soliton solution of equation (22) is given

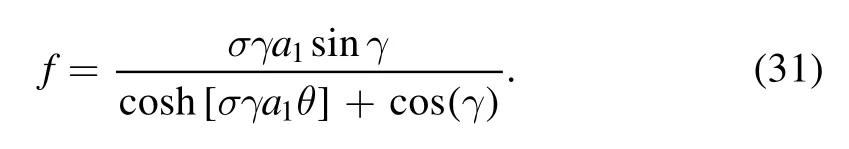
Similarly,the N-soliton solution of model can be expressed in the form

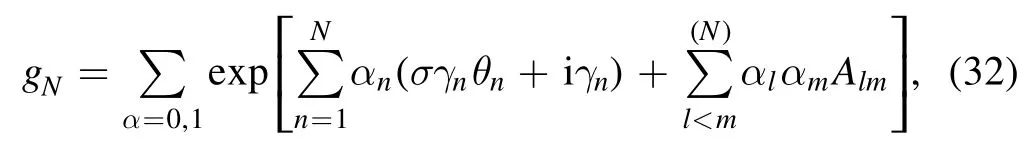
4.Bäcklund transformations and the infinite number of conservation laws

Conservation laws play an important role in studying the properties of equations.As we all know,bäcklund transformation is an important tool to find conservation laws.In this section,based on Hirota bilinear method,the Bäcklund transformation of the ILW equation is formulated.Then,the infinite number of conservation laws of ILW equation are constructed from the Bäcklund transformations in bilinear form.

4.1.Bäcklund transformations

Let F be another solution of equation (22),that is,

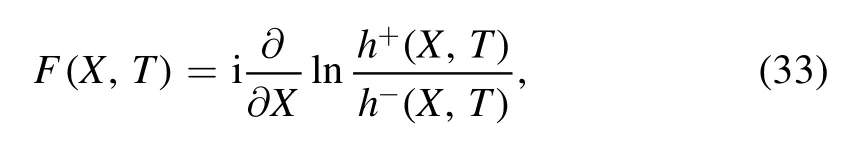
similarly,equation (22) can be transformed into the bilinear equation

The relation connecting the two solutions f and F,Bäcklund transformations in bilinear form,are given as

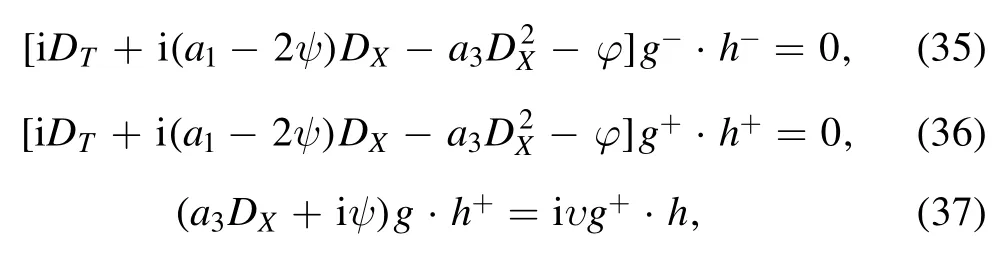
where ψ,φ and υ are arbitrary constants.Setting

and using the following properties of bilinear operators

we can obtain

Therefore,equations (35)–(37) are Bäcklund transformations in bilinear form of equation (22),the proof is complete.

4.2.The infinite number of conservation laws

To transform Bäcklund Transforms equations (35)–(37) into the form of the original variable,we introduce the potential functionsand

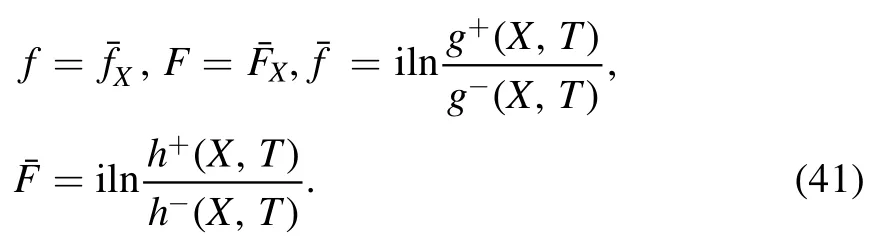
The following relations are derived from equation (26)

and the similar relation for F,h−and h+.Then we can get the space part of the Bäcklund transformation in original variables as follows

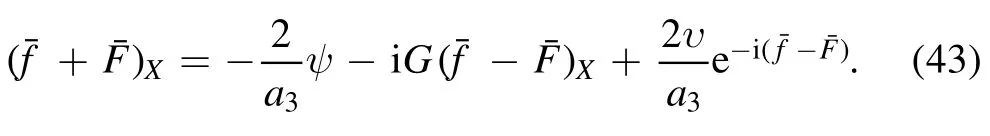
The time part of the Bäcklund transformation,equations (35) and (36),can be rewritten as follows

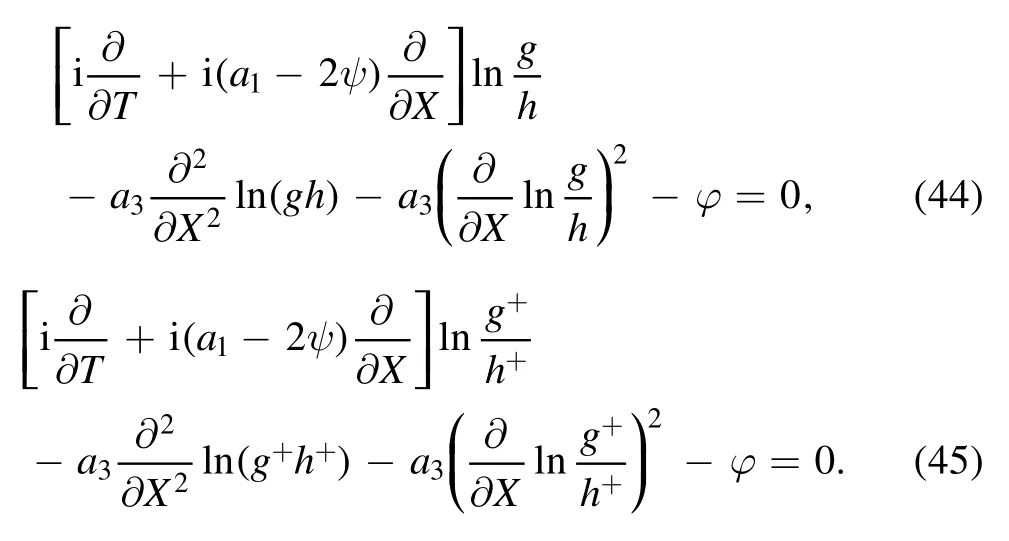
Subtracting equation (44) from (45),then we can obtain the time part of the Bäcklund transformation in original variables as follows

Equations (43) and (46) are Bäcklund transformations in the original variables.Since the explicit Bäcklund transformations in original variables are obtained,the infinite number of conservation laws can be easily derived.We can rewrite equation (43) as

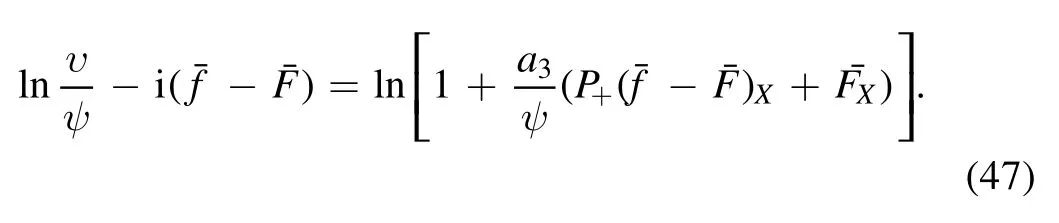
Considering the expansion of the power series:substituting it into equation(47),and compare the 1/ψnterm on both sides of the equation,we can get

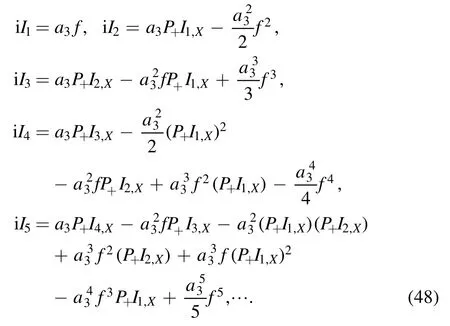
It is important to notice that the iInis non-trivial for each n,because every term has Fn/n in it,which is purely a power of F.Using the boundary conditionas|X|→∞thatwe can obtain the conserved quantity

Further,the infinite conserved quantity Encan be written as

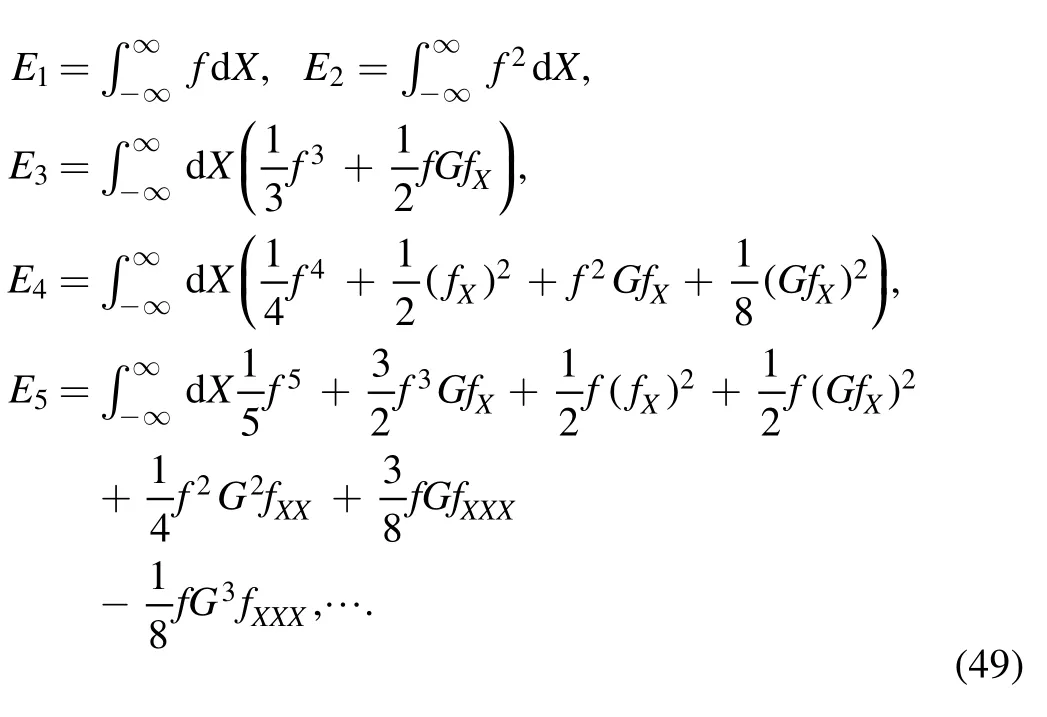
It is well known that E1represents the conservation of mass of internal solitary waves.E2and E3represent the conservation of momentum and energy of internal solitary waves,respectively.However,the physical meaning represented by other conservation laws needs to be studied in future.

5.The fission property of internal solitary waves

The fission is an important property of algebraic solitary waves,especially in the ocean and atmosphere.In section 4,we have studied the conservation law of the model,and on this basis,we will study the unsteady behavior of the model.Actually,the internal solitary waves that we have derived in this paper cannot be called the common‘soliton’.That is because in the nonlinear process,as time evolves,an internal solitary wave at the initial time can split into a series of internal solitary waves.Based on the conservation laws we have obtained,we study the fission process of internal solitary waves to predict the amplitude of emergent the solitary waves.

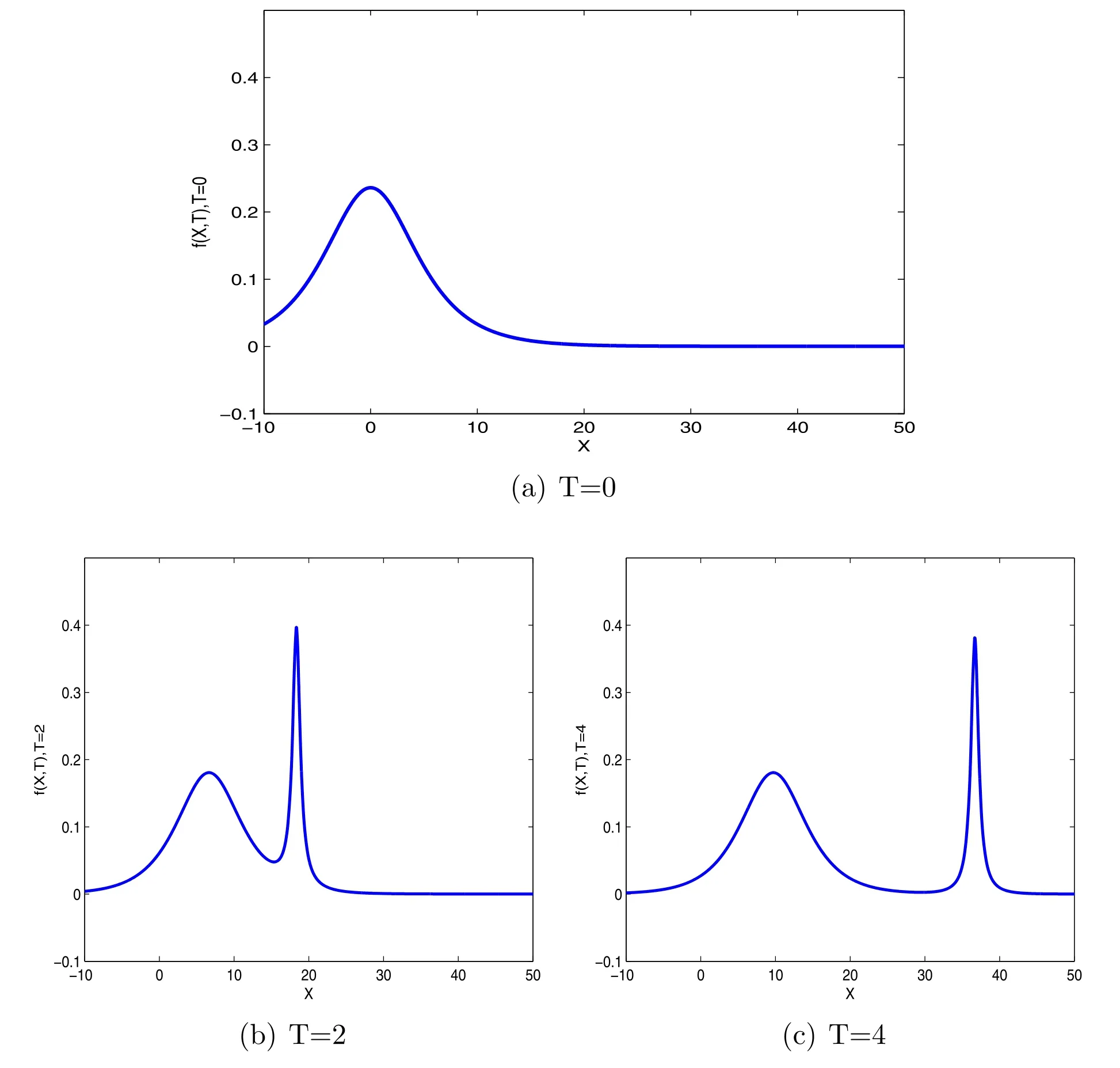
Figure 1.Fission process of the internal solitary wave.

We take the initial value of internal solitary waves as follows

wheref0=c0σγa1sinγ,γ is an arbitrary real parameter with 0 ＜γ ＜π.Without loss of generality,it is assumed that the initial waves asymptotically split into N solitons with different amplitudes and phases in the form

wherefn=cnσ nγ a1sin(nγ),μn(n=1…N) are some phase shift.

According to the conservation laws that we have derived in section 4,we can get the conserved quantities E1and E2from the initial value equation (50) at T=0,

Meanwhile,as time evolves,the conserved quantity can be regarded as the sum of the associated with each emergent solitary wave after fission.We can get

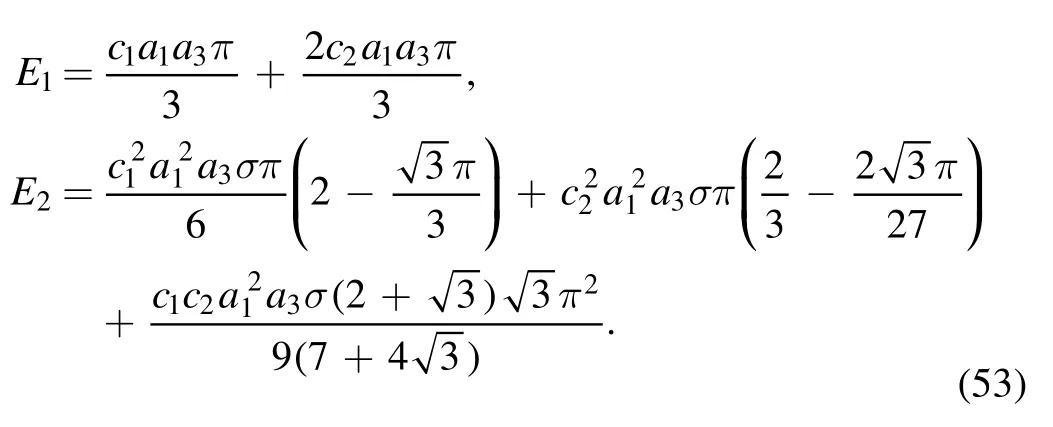
Here,we only consider the case when n=2,that is,it splits into two solitary waves after fission.Similarly,more fission processes can be derived.Equating corresponding quantities in equations (48) and (49),we find that

Without loss of generality,assuming that γ=π/6,h1/h0=4,a1a3=1/2,c0=2,we can get

We have analyzed the fission phenomenon of internal solitary waves theoretically,and then we will verify the fission phenomenon of the internal solitary wave through numerical simulation in figure 1.

It can be seen from figure 1 that the internal solitary wave is initially formed,and as time goes by,the initial internal solitary wave begin to split into two solitary waves with different amplitudes.Through the comparison of them,we find that solitary waves propagate in the same direction.In addition,the solitary waves with smaller amplitude lag behind the solitary waves with larger amplitude,and the distance between them is getting larger and larger with the passage of time.Here,we only considered the case where one solitary wave splits into two solitary waves,and more fission can be derived similarly.It is not difficult to imagine that these two solitary waves will continue to split into more solitary waves.Eventually a regularly arranged solitary wave train is formed,with large and strong solitary waves arranged in the front and small and weak solitary waves arranged in the back.It is well known that the fission of algebraic solitary waves in atmosphere may be one of the formation mechanism of squall lines[8].In the ocean,the study of the fission allows us to predict the amplitude and location of incoming solitary waves,thereby avoiding some Marine hazards.This is of great significance to human exploration of the ocean and Marine work.

6.Conclusions

In this paper,using the multi-scale analysis and perturbation methods,ILW equation has been derived to describe the propagation of internal solitary waves in the ocean of finite depth.Further,based on the Hirota bilinear method,we derive the Bäcklund transformation in bilinear form and infinite number of conservation laws.As is known to all,E1,E2and E3can represent the conservation of mass,momentum and energy of internal solitary waves,respectively.However,the physical meaning represented by other conservation laws needs to be studied in future.Finally,we analyze the fission phenomenon of internal solitary waves theoretically and verify it through numerical simulation.All of these have potential application value for further comprehension on ocean internal solitary waves.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No.11975143),the Nature Science Foundation of Shandong Province of China (Grant No.ZR2018MA017),the Taishan Scholars Program of Shandong Province,China (Grant No.ts20190936),and the Shandong University of Science and Technology Research Fund,China(Grant No.2015TDJH102).