大气压氩气直流放电一维仿真电子崩分析

沈阳理工大学 王 薇 李洪超

针对大气压氩气直流放电，建立一维仿真模型，设置了初始电子的密度和确切位置，通过求解，得到如下结果：初始电子崩由阴极的初始电子碰撞电离产生，电子碰撞电离产生17代电子之前，电子每发生一次碰撞电离走过的路程和时间都几乎未发生变化，电子漂移的速度是恒定的，电子崩的发展速度是恒定的，在17代电子到20代电子时，电子每发生一次碰撞电离走过的路程和时间变长，电子漂移速度减慢，且电子在从初始位置走到0.9mm时，电子数随位置变化曲线呈指数型，在0.9mm后电子数分布在指数趋势线下，仿真分析结果与reather相关理论描述的相一致。

等离子体常被看作是除固、液、气之外，物质存在的第四态。气体放电是产生等离子体的主要方式。本文主要对大气压下氩气直流放电电子崩进行仿真分析。

1 模型定义

1.1 几何模型

假设电极的尺寸远远大于气隙间距，选用一维模型，如图1所示，模型由两个电极组成，一个电极连接恒定电压，另一个电极接地，极间距为d，背景气体为纯氩气。

图1 氩气直流放电模型

1.2 数学模型

通过求解电子密度的漂移扩散方程来计算电子密度：

表1 氩气碰撞电离反应

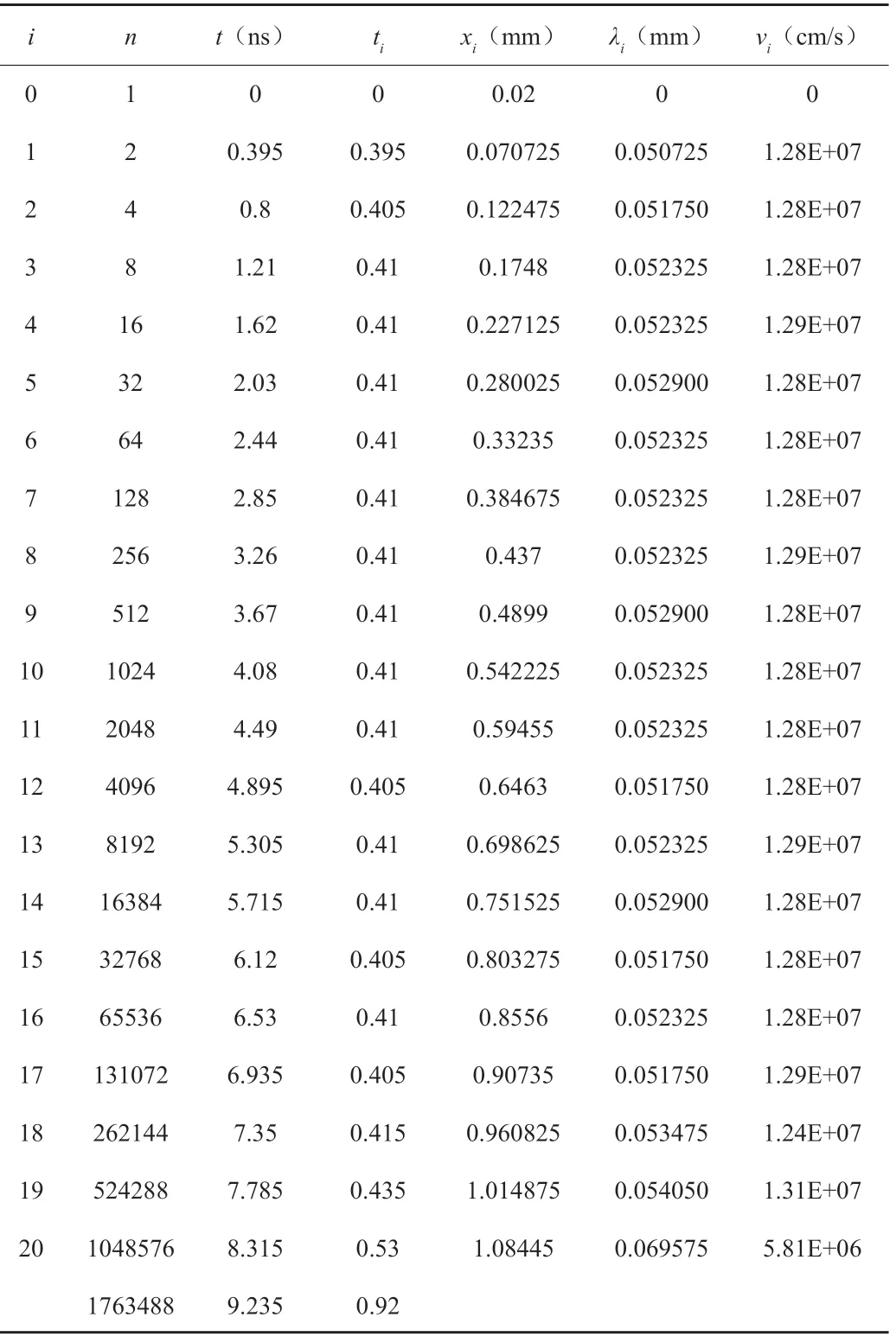
表2 电子崩计算数据

1.3 仿真参数设置

仿真在一个大气压下进行，电极间距为1.15mm，阴极于左侧（接地），阳极（右侧）施加800V直流电压，设置距离阴极0.02mm处有一个电子。化学反应设置如表1所示。

1.4 求解设置

采用有限元方法求解偏微分方程，将连续的求解域离散成为一组单元的组合体，最终形成一个离散的线性方程，解向量的求解用直接求逆得到。

2 仿真结果及分析

在所有时刻的电子离子密度图中针对性地选取电子数为21，22，...219，220时刻的电子密度数据进行计算（如表2）。

表2中i为碰撞电子次数，n为电子数，t为发生第i次碰撞电离的时间，ti为相邻两次碰撞电离的时间差，xi为电子发生第i次碰撞电离电子数峰值位置，λi为电子发生相邻两次碰撞电离走过的距离，vi为相邻两次碰撞电离走过距离间的电子漂移速度。其中，n由电子密度空间分布结果积分计算，xi在仿真电子密度空间分布结果的导出数据中获取，拟取相邻两次碰撞电离的电子数峰值位置的差值，vi由

以下公式计算：

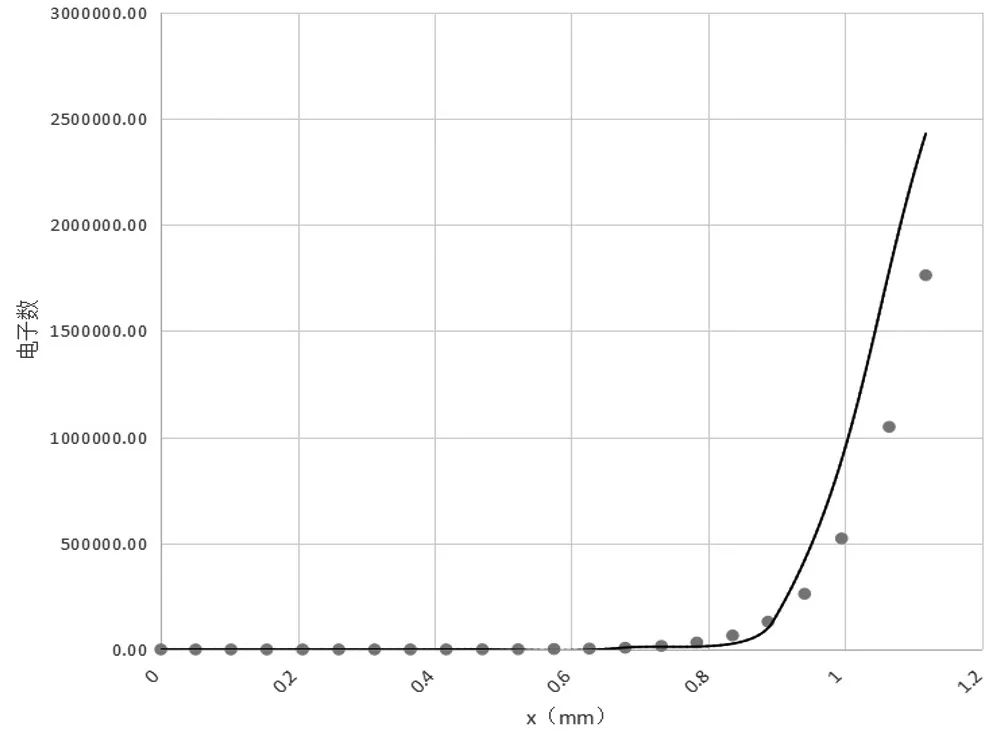
图2 电子数随位置变化图像（黑色曲线为指数趋势线）

从表中ti的计算数据可以看出：

（1）电子碰撞电离次数i小于17，电子发生一次碰撞电离的时间大约0.41ns，走过的距离数值大概在0.052325mm，电子的漂移速度vi约1.28E+07cm/s，基本未发生变化，在此期间电子崩的发展在时间和速度上都可以看做是恒定的。

（2）在电子碰撞电离次数i大于17时，电子发生一次碰撞电离的时间越来越长，在9.235ns时，电子数为176320，此时上次碰撞电离产生的所有电子还未全部发生下一次碰撞电离，却历时0.92ns，时间是i小于17时电子碰撞电离时间的两倍之余，电子漂移速度也逐渐减慢，证明电子在发展到第17代电子后，碰撞电离发生的越来越少，电子崩发展速度变缓慢。

为了更直观地看出电子崩发展的情况，将表2中的电子数数据，及电子数对应位置数据绘制成数据点，如图2所示，可以看出在x小于0.9mm时，所绘制数据点与指数趋势线大致是吻合的，即在电子在0到0.9mm之间发生碰撞电离产生的电子数随位置呈现指数上升的趋势，在0.9mm后，电子数普遍分布在指数趋势线下，说明电子的碰撞电离程度有所减弱，这种情况是由于空间中离子浓度的升高，加强了正极性空间电荷，使得外加电场对电子加速的作用，降低了电子的电离能力，这与raether判据中描述是相一致的。

结论：气隙中初始电子崩由设置在阴极附近初始电子发展而来，初始电子崩在阳极发展到阴极的过程中，电子碰撞电离产生17代电子之前，电子每发生一次碰撞电离走过的路程和时间都几乎未发生变化，电子漂移的速度是恒定的，电子崩的发展速度是恒定的，在17代电子到20代电子时，电子电子每发生一次碰撞电离走过的路程和时间变长，电子漂移速度减慢，且电子在从初始位置走到0.9mm时，电子数随位置变化曲线与指数趋势线相吻合，在此期间电子数呈现指数变化的，在0.9mm后电子数分布在指数趋势线下，说明电子碰撞电离减少，与数据分析结果一致，仿真分析结果与reather相关理论描述的相一致。