隔离型准Z源逆变器滑模控制策略研究

李 山，蒋 力，陈 艳，姜伟豪

（1.重庆理工大学 电气与电子工程学院，重庆 400054；2.重庆市能源互联网工程技术研究中心，重庆 400054；3.中国船舶重工集团海装风电股份有限公司，重庆 401122）

随着传统不可再生化石能源的过渡使用，其带来的温室效应、能源枯竭和环境污染等问题促使人们向着绿色、高效和环保的新能源探索和开发。其中，太阳能以其资源丰富、绿色清洁、储量巨大等优点，成为全世界大力研究发展的热点方向。光伏发电系统的核心是逆变器系统，传统逆变器在面对光伏发电系统输入电压多变等复杂情况下，存在外界抗干扰能力差、输入电压范围小、效率低、故障率大等问题。针对此类问题提出隔离型准Z源逆变器，该逆变器属于Z源类逆变器，具有输入电压范围大、高升压比、电气隔离等优势［1］，适用于光伏发电系统。

隔离型准Z源逆变器因其特殊的拓扑结构使系统具有明显的非线性。在输入电压发生变化时，其直流链电压会出现超调和振荡，导致输出电压和电流稳定性变差。为了更好地实现Z源类逆变器的直流链电压控制，国内外学者进行了大量研究，成功地将滑模变结构这种非线性控制策略运用于Z源类逆变器的控制。薛阳等［2］设计了一种双滑模变结构控制策略，实现了对准Z源逆变器的控制，有效提高了准Z源光伏并网逆变器系统的鲁棒性和并网电能质量。方番等［3］针对储能型准Z源逆变器系统，提出采用具有积分补偿的固定开关频率积分滑模电流控制器，来保证系统鲁棒性和快速响应。Shinde等［4］提出了一种基于等效控制的积分滑模控制器，用于实现Z源逆变器的电容电压恒定控制，但该滑模控制器对于输入电压扰动的情况，控制效果不佳。

本文基于隔离型准Z源逆变器，设计了一种基于分段幂次趋近律的滑模控制策略，在输入电压和直流链参考电压大变动的情况下，对比传统的滑模控制策略，前者具有更优的动态响应速率和鲁棒性，能够显著改善隔离型准Z源逆变器直流链电压及输出电压、电流特性，使整个逆变器系统具有很好的动态和稳态性能。

1 隔离型准Z源逆变器建模

Z源类逆变器与传统的电压型以及电流型逆变器最大的区别在于：前者在工作过程中，其上下桥臂是可以直通的［5］，这种情况如果发生在后者的工作过程中，则会发生严重的电路短路导致逆变器的损坏。因此，Z源类逆变器在正常工作时会经历2个工作模式，直通模式和非直通模式。隔离型准Z源逆变器的等效电路如图1所示。

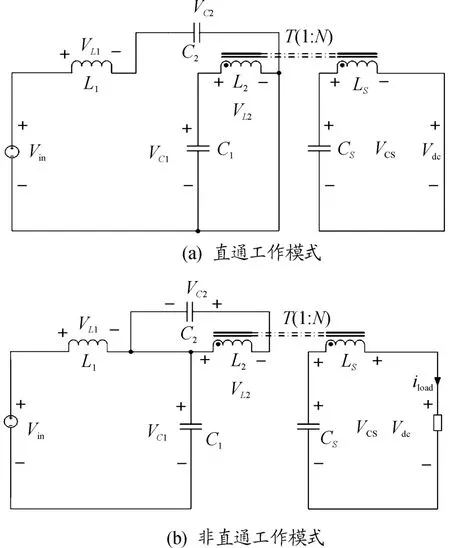
图1 隔离型准Z源逆变器等效电路图

在图1中，Vin为逆变器输入电压，VL1为电感L1上的电压，VL2为变压器原边电感L2上的电压，VC1为变压器原边电容C1上的电压，VC2为电容C2上的电压，VCS为变压器副边电容CS上的电压，Vdc为直流链母线电压，iload为等效负载电流。经过对隔离型准Z源逆变器的2个工作模式的分析可得：

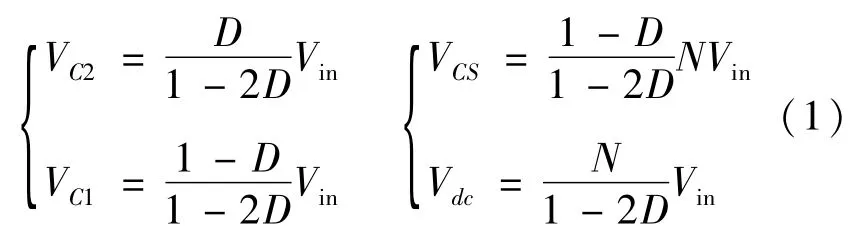
由式（1）可知：在输入电压确定的情况下，通过调节直通占空比D，即可改变隔离型准Z源逆变器的直流链电压，实现对逆变器输出电压、电流的控制。

在利用状态空间平均法对逆变器进行小信号建模后，可得到直通占空比到直流链电压的传递函数：

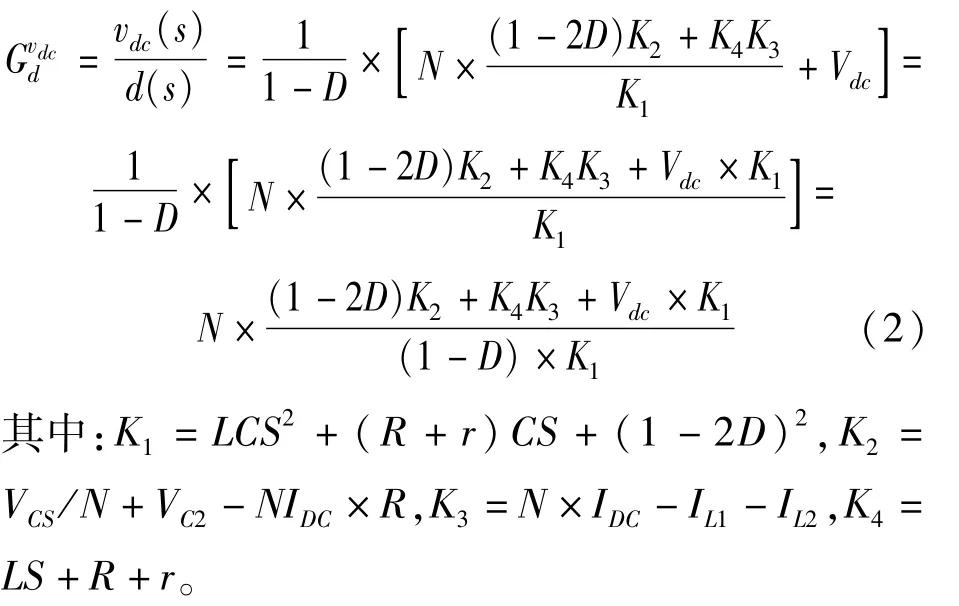
从式（2）可以看出：由于高频隔离型准Z源逆变器的特殊工作特性，其直通占空比到直流链电压的传递函数右半平面存在零点，因此该系统会出现非最小相位现象。在输入电压出现扰动的时候，非最小相位现象会使整个逆变器的输出呈现超调和振荡，严重影响逆变器的各项性能指标。为了保证逆变器稳定的输出，需要对直流链电压实现稳定控制。

由式（1）可得：

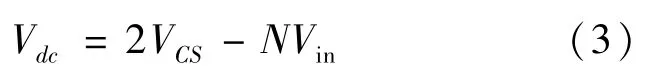
式中Vdc是直流链母线电压，基于Z源阻抗的网络特性可知该电压为一脉动方波，这在实际工程环境中难以测量控制。由上式得知，在Vin明确的情况下，可以通过测量控制副边电容上的电压VCS来实现对直流链母线电压Vdc的控制。

令直流链母线电压Vdc的目标控制参考值为可得：

2 滑模控制器设计

本文选择简单升压SPWM调制策略［6］产生PWM波进行控制。整个控制系统框图如图2所示。

图2 隔离型准Z源逆变器控制系统框图

根据隔离型准Z源网络的建模分析，可以推导出隔离型准Z源网络状态变量：

设计滑模面方程：

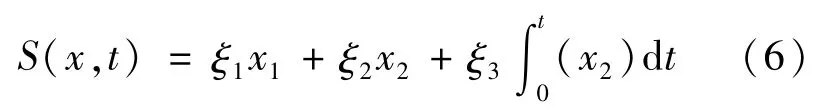
式中，ξ1、ξ2、ξ3为滑模控制系数，满足条件 ξ1、ξ2、ξ3≠0。

在创建好滑模面后，需要对其存在性和可达性进行验证，这一过程通常采用Lyapunov稳定性理论［7］。在这里创建Lyapunov函数：

根据隔离型准Z源逆变器的开关管的工作特性，创建开关函数：

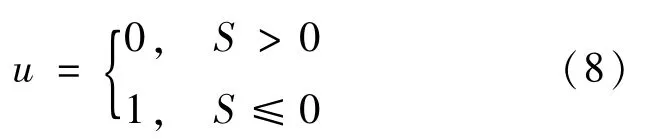
下面进行滑模面的存在性和可达性证明：

①滑模面存在性证明：

在受控系统从负向方向运动趋近于滑模面时，对S取极限求导：

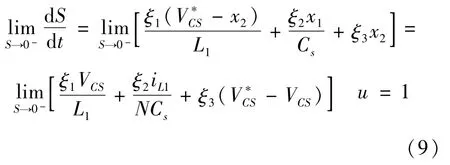
在当系统处于滑模面邻域中时，VCS实际测量值近似等于参考值。因为直通占空比D∈［0，0.5），可以得到VCS＞0，iload＞0。现如果满足ξ1、ξ2＞0，则式（9）大于0。

同理，当受控系统从正方向运动趋近于滑模面时，对S取极限求导：

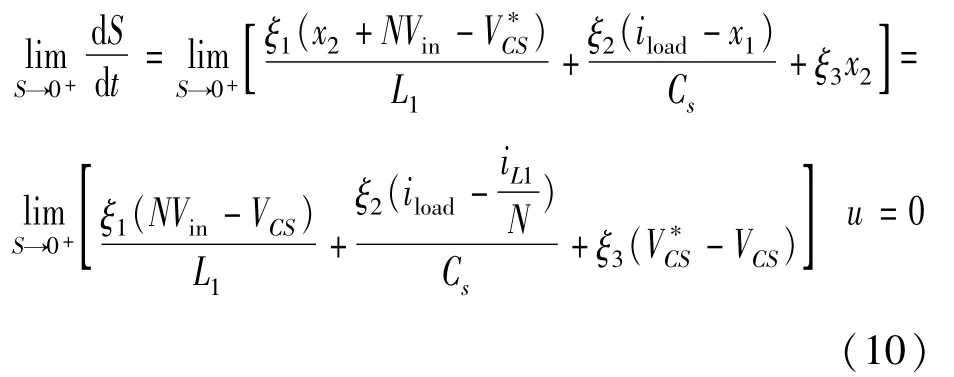
式（10）中的第2项和第3项近似等于0，根据直通占空比D∈［0，0.5），可得NVin-VCS＜0。现如果满足 ξ1＞0，则式（10）小于0。

由式（9）和式（10）得知：在适当选取滑模系数的情况下，系统从任意初始点开始运动逼近至滑模面的过程中，总存在SS·＜0，滑模面存在性得证。

②滑模面可达性证明：假设系统运动初始点位于S＞0的区域，且系统无法从该点抵达滑模面。由开关函数式得知此时开关管S5处于关断状态，整个逆变器处于非直通工作模式，故可得直通占空比最小极限值Dmin＝0，则VCS＝NVin，iL1／N＝iioad，对S取极限求导：

如果满足前提条件 ξ3＜0，则式（11）小于0。

同理，假设系统运动初始点位于S＜0的区域，且系统无法从该点抵达滑模面。此时，开关管S5处于导通状态，整个逆变器处于直通工作模式，直通占空比最大极限值Dmax＝0.5，则VCS＝∞，对S取极限求导：

如果满足前提条件 ξ1＞0，ξ3＜0，则式（12）大于0。

由式（11）和式（12）可得：在满足前提条件ξ1＞0，ξ3＜0的情况下，假设系统从任意初始点出发，不能抵达滑模面，但实际总存在SS·＜0，由Lyapunov稳定性理论可得，假设不成立，故滑模面的可达性得到证明。

综上所述，当滑模面参数满足 ξ1＞0，ξ2＞0，ξ3＜0，所设计的滑模面存在且可达。

在整个滑模控制的设计中，滑模面存在且可达是实现滑模控制的基础，它表示了受控系统能够在状态空间中从初始点运动至滑模稳态面。为了进一步优化运动轨迹，需要引进“趋近律”对系统的收敛轨迹进行设计控制。本文设计的分段幂次趋近律结构如下：

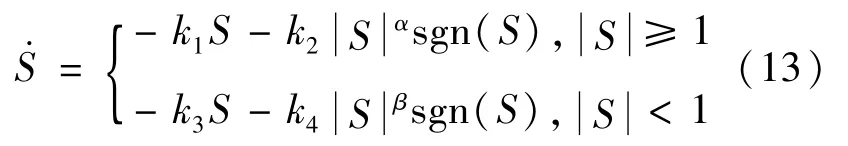
式（13）中，k1≥0，k2＞0，k3≥0，k4＞0，k1+k2＝k3+k4，α＞1，0＜β＜1。

所设计的趋近律有以下特点：

整个趋近运动分为2个过程：｜S｜≥0和｜S｜＜0通过幂函数的控制特性，系统无论在哪个阶段都能获得可观的趋近速度。与其他传统趋近律相比，该趋近律能保证系统在有限时间内到达滑模面，同时在到达滑模面后无抖振现象发生。

将滑模面（6）和分段幂次趋近律（13）联立：

对本文所要设计的分段幂次趋近律滑模控制器而言，将式（5）代入式（14）可得：

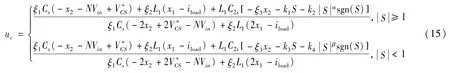
经分析可知，控制量uc为所设计的分段幂次趋近律滑模控制器的等效输出信号，是直流链电压控制中需要的直通占空比D。

3 仿真与实验

为了验证本文所设计的分段幂次趋近律滑模控制器的控制性能，设置传统滑模控制器的对比项，分别在输入电压变化时和直流链电压参考值变化时进行隔离型准Z源逆变器的仿真和实验。隔离型准Z源网络的参数设置如下：电感L1＝1 mH；电容CS＝600 uF；开关频率f＝20 kH；变压器变比N＝4。

设置初始输入电压为60 V，当逆变器输入电压在0.2 s时增大25%，在0.3 s时跌落25%回到初始值。传统滑模控制和分段幂次趋近律滑模控制下的逆变器系统的直流链电压和变压器副边电容电压的波形变化如图3所示。

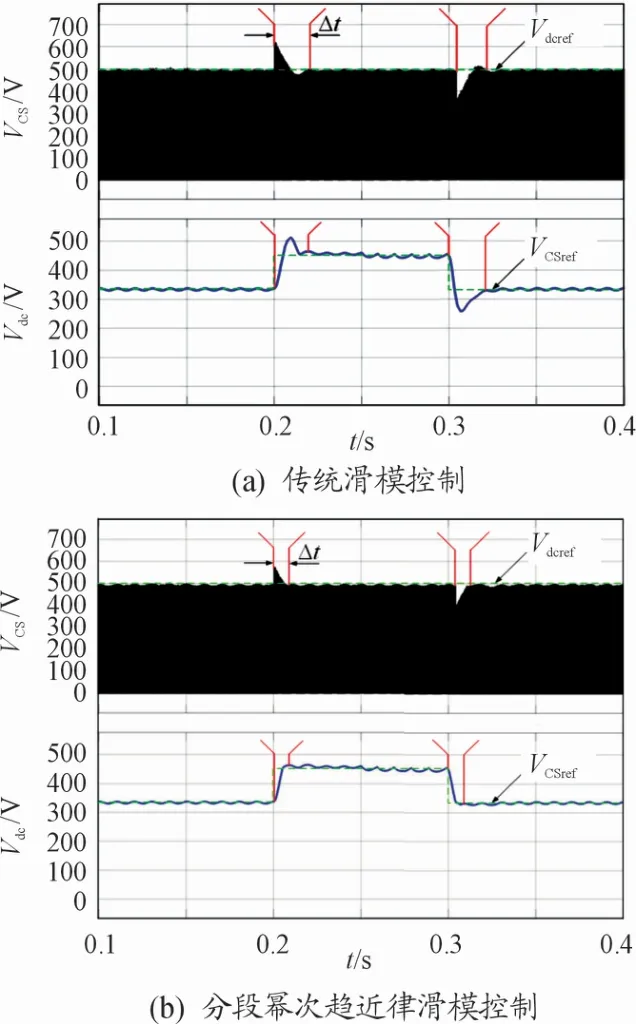
图3 输入电压变化时，Vdc和VCS仿真波形

从图3可以看出：当输入电压变化时，采用传统滑模控制的逆变器需要Δt＝23 ms才能重新恢复稳定，且在恢复稳定的过程中存在着较大的超调量，约为21.32%。而采用分段幂次趋近律的滑模控制的逆变器系统只需Δt＝10 ms就能重新稳定在新的电压值，振荡时的超调量约为9.47%。由此对比可以看出：本文所设计的直流链电压控制策略在对直流链电压和变压器副边电压的控制上有着良好的动态响应能力和抗干扰能力。

设置初始直流链电压参考值为600 V，当逆变器的直流链电压参考值在0.2 s时跌落25%，并在0.3 s时恢复至初始值，传统滑模控制和分段幂次趋近律滑模控制下的逆变器系统的直流链电压和变压器副边电容电压的变化波形如图4所示。

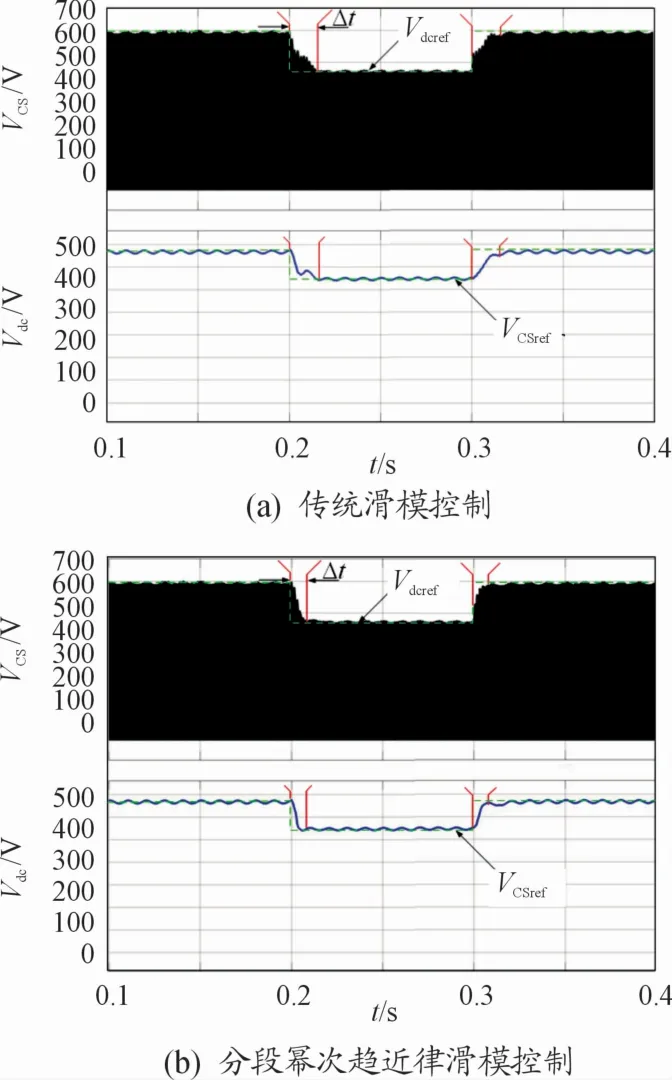
图4 直流链电压参考值变化时，Vdc和VCS仿真波形

从图4可以看出：当直流链电压参考值变化时，采用传统滑模控制的逆变器系统需要Δt＝24 ms才能重新恢复稳定，且在恢复稳定的过程中变压器副边电容电压出现了一定的振荡且反应速度较慢。而采用分段幂次趋近律的滑模控制的逆变器系统只需要Δt＝8 ms的时间就能重新跟踪至新的直流链电压值，所需稳定时间短，过渡曲线较为平缓。由此对比可以看出：在本文所设计的分段幂次趋近律滑模控制策略下的逆变器在直流链电压参考值改变的情况下，仍具有优良的快速响应能力和稳定性。

为了验证本文提出的直流链电压控制策略的正确性和可行性，基于仿真，将传统滑模控制策略与分段幂次趋近律滑模控制策略进行对比实验，检测其在输入电压和直流链电压参考值改变情况下的逆变器直流链电压和变压器副边电容电压实验波形图。

输入电压变化时，在不同控制策略下的隔离准Z源逆变器的直流链电压和变压器副边电容电压实验波形如图5所示。

图5 输入电压变化时，Vdc和VCS实验波形

从图5中可以看出：在分段幂次趋近律滑模控制下的逆变器的直流链电压和变压器副边电容电压在输入电压发生变化后，能够很快重新稳定，其超调量和稳定时间均远小于传统滑模控制。

当直流链电压参考值发生变化时，在不同控制策略下的隔离准Z源逆变器的直流链电压和变压器副边电容电压实验波形如图6所示。

图6 直流链电压参考值变化时，Vdc和VCS实验波形

当直流链电压参考值变化时，分段幂次趋近律滑模控制下逆变器的直流链电压和变压器副边电容电压能够在较短的时间内重新稳定，对比传统滑模控制则需要更长的时间来进入下一稳态，实验结果与仿真结果基本一致。

4 结论

本文首先分析了隔离型准Z源逆变器的工作模式，在利用状态空间平均法对逆变器进行小信号建模后，推导出了直通占空比到直流链电压的传递函数；之后在滑模控制器的设计中，进行了滑模面和趋近律的构造；最后，在仿真软件及实物平台上进行了验证。所设计的控制器对比传统滑模控制器在隔离型准Z源逆变器的直流链电压控制性能上，动态响应速率更快，超调量更小。