核燃料裂变破碎过程中静力学和动力学受力分析的对比研究
王 斐,谢东升,张瑷月,康 锐,吴 璐,潘虎成
(1.中国核动力研究设计院第一研究所,成都 610041;2.东北大学 材料学院 材料各向异性与织构教育部重点实验室,沈阳 110819)
目前商用的核反应堆最核心的部件即为燃料组件[1-3],而Zr[4-5]和UO2[6-8]是常用的核材料,其一般是由单片式的UO2/Zr[9-10]燃料板组成。该组件类似于金属基的复合材料,即由微米尺度的UO2颗粒弥散分布于Zr基体合金的内部而成,所采取的制备工艺一般分为球磨制粉、混料、热等静压以及后续的挤压或轧制等大变形以降低孔隙率,从而达到控制形状和控制性能的双重目的。然而,在UO2/Zr单片式燃料板的实际服役过程中,往往面临着严苛的高温[11]、高 压[12]和辐照[13-14]等环境,将不可避免的会在UO2内部或板内界面处的孔隙聚集大量的高温裂变气体,并在如此复杂的多场耦合作用下,对Zr合金的基体发生迭代式的爆炸冲击作用,会有可能对Zr合金的基体带来塑性损伤甚至破坏的风险。因此,系统研究UO2/Zr单片式燃料板服役过程中的裂纹扩展行为以及受力情况,对保障核反应的正常运行具有重要工程意义。
静力学法[15-17]又称“主应力法”,是在对实际工程问题进行简化的基础上建立平衡方程、屈服准则和边界条件后求解变形力的一种近似方法。尽管有限元的动力学分析方法越来越被广泛地应用于变形力的求解与预测[18-24],静力学法在工程上的应用也从未间断[25-26]。静力学的受力分析方法已被广泛应用于挤压、轧制、锻造和拉深等塑性变形加工等问题上。譬如,邓磊等[27]基于静力学方法分析了铝合金筋板构件挤压变形过程的受力情况,其计算结果与数值模拟及试验结果一致。张晗等[28]基于静力学方法计算了圆棒料锥模拉拔力,结果表明,求解的拉拔力符合工程要求并能够实现设备吨位的选择。静力学方法作为一种简便的评估方法,可对受力情况实现快速有效的评估,周期短、成本低,因此在工程应用中始终受到学者们的青睐。
在本研究中,为了定量分析气孔裂变爆炸过程中应力与变形情况,拟首先采用静力学法对该工况进行应力预估,其次进行有限元的动力学研究以验证静力学分析的准确性。动力学方法主要涉及对建立的核燃料板进行温度分析,根据温度计算出冲击压力峰值,然后将该冲击压力变化作为冲击载荷边界条件应用于动力学冲击分析,分析软件为ANSYS LS-DYNA 19.0。核燃料板包壳采用Zr合金,芯体材料为UO2,各材料的力学性能如下表所示,本次有限元分析材料模型利用Johoson-Cook失效准则进行模拟。计算中所用的Zr合金参数选用的是经球磨制粉压制后的Zr-2型的核用锆合金,具体的工艺流程主要包括球磨、混粉、烧制和挤压等工序,经制备加工后锆合金的关键力学性能参数如表1所示。

表1 材料力学属性
1 工程法静力学近似分析
将气体裂变过程简化为球体受到内高压发生塑性变形乃至破坏的过程,并利用工程法静力学对该过程进行近似力学分析。
UO2/Zr燃料类似于金属基的复合材料,即由微米尺度的UO2颗粒弥散分布于Zr基体合金的内部而成,经辐照后产生气孔的形态普遍为球形,这一现象已经被扫描电镜等分析测试方法普遍证实[29]。因此首先可以将核燃料假设为一个球体,内孔半径为r0,球体半径为R0(图1所示),那么当内孔受内压为p的条件下,如果发生塑性变形,则整个球体截面上沿半径R方向上的点的应力大小可以通过工程法静力学近似求解得到。
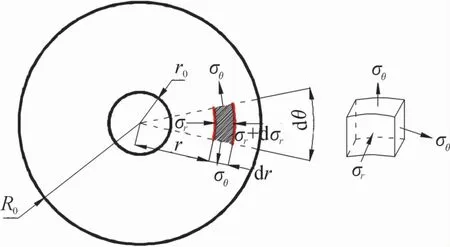
图1 球体受力示意图
根据静力平衡条件,列半径方向上的平衡方程为:
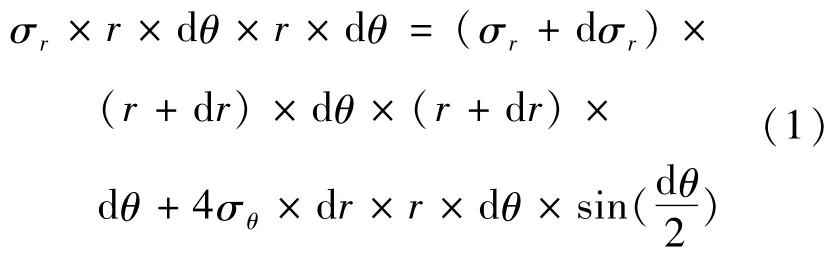
将式(1)进行化简,忽略高阶项影响,可得到简化的平衡微分方程:
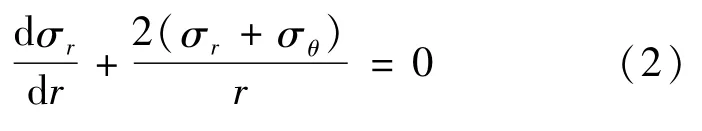
代入屈服准则公式:σθ-(-σr)=σs,将其代入式(2)可得:

两边积分可得:
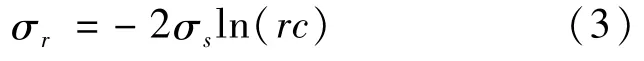
利用边界条件,当r=R0时,径向应力为0,可得:
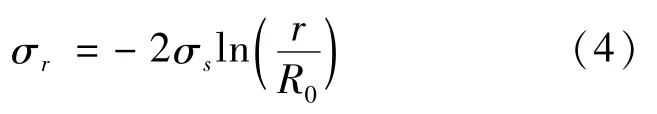
由式(4)可得当内层发生塑性变形时,r=r0,此时内压力p为:
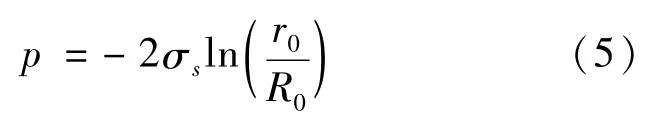
由式(5)可见,气体裂变过程中,二氧化铀或者锆合金发生塑性变形乃至塑性失效,主要与气体大小和材料自身屈服强度有关,表现为自然对数关系,内层受静高压条件下易于失效,塑性失效破坏从内层逐渐外扩。
另外,当外部完全发生塑性变形乃至失效时,由于此时径向应力为0,则整体受力可以看做一定壁厚的壳体,其壁厚为R0-r0,由平衡条件可得:

依据 σ1=σ2=σθ和 σ3=0,代入屈服准则可得:

由式(7)可以看出,外壁发生塑性变形所需内层受内压值比较大。由此可见,受单一的内静高压,不易使外层发生塑性变形乃至失效,但冲击动力载荷却有所差异。
2 数值模拟分析
2.1 力学分析有限元模型
燃料板外部为Zr合金包壳,内部为UO2芯体,同时夹杂以小型的气孔。将气孔、UO2和Zr基体均假设为球形,故符合轴对称问题,可以简化为平面问题,为实现在LS-DYNA中施加面载荷,以球心为中心点建立薄片三维体为几何模型(厚度为0.005 mm),厚度方向仅划分一层单元,进而大幅度减小有限元计算量,提升有限元求解速度。
本次气体爆炸破碎有限元分析中,建立的有限元模型如图2所示。如前所述,由于燃料板厚度相较于长度及宽度变化极小,可将整个模型简化为平面应变问题,有限元网格划分时板厚度方向为单层,又因UO2芯体在燃料板中弥散分布,可进一步将其简化为轴对称问题。尺度最小的三维模型由Zr合金基体、2个UO2芯体颗粒,裂变气孔(包覆于UO2芯体)组成,建立的具有极薄厚度的1/4扇形薄板模型厚度为0.05 mm,Zr合金基体半径为40 mm,UO2芯体颗粒内径为1 mm,外径为5 mm,与Zr合金基体接触,裂变气孔半径为1 mm,包覆于UO2芯体,如图2所示。
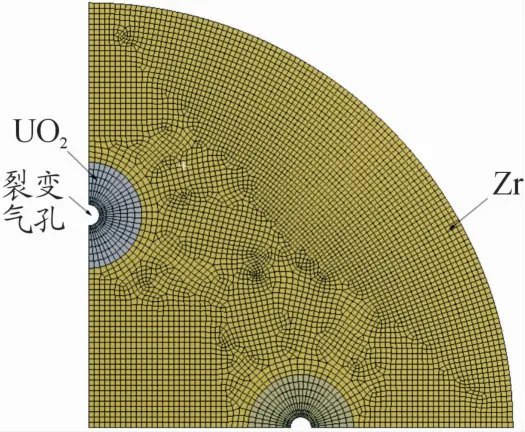
图2 燃料板有限元模型
2.2 温度分析及冲击峰值确定
核燃料内的气体在裂变过程中将产生高温,高温膨胀引起的脉冲载荷会对燃料基体产生显著的冲击作用。因此,裂变气体可假设为内热源,在温度求解过程中,几何模型可等效为圆柱体,根据轴对称进行简化并进行二维平面分析。内孔的半径为1 mm,UO2的直径为5 mm,Zr的尺寸为10 mm×20 mm,Zr的边界温度设定为300℃。依据裂变传热模型及分析计算,利用有限元软件ANSYS LSDYNA 19.0可求解出核燃料板在裂变发生3 ms后的气孔中心处的温度6 117℃。
根据修正的范德瓦尔方程可以求得一定温度和体积下的内部压力水平,其中范德尔方程为:
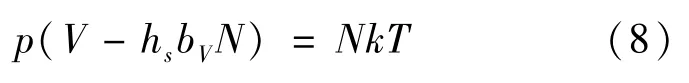
其中,p为气体压强,即所求的冲击载荷(Pa);bV=8.5×10-29m3,为裂变气体Xe的范德瓦尔常数;V为气体体积(m3);hs=0.6,为量纲为一化常数;N为总气体原子数;k=1.381×10-23J/K,为玻尔兹曼常数。将上述计算所得的温度参数代入式(8),最终求得迭代式冲击载荷峰值p约为800 MPa。温度升高过程中,裂变气体发生膨胀进而对周围的UO2诱发内高压,在较大的内压力作用下UO2颗粒和Zr基体会被逐渐破坏。
2.3 Zr基体双孔UO2颗粒核燃料板内气体裂变过程的有限元分析
图3所示为Zr合金基体双孔核燃料板模型气体裂变过程不同时刻燃料板等效应力的分布规律与塑性失效破碎情况。由图3(a)可知,当核燃料发生裂变过程中,孔内气体冲击压强达到峰值800 MPa时,最先受到破坏的是与气孔接触的UO2颗粒,在双孔UO2颗粒尺度下,脆性较大的UO2颗粒绝大部分已破碎,圆孔周围受力大小沿圆周方向基本相同,符合圆孔内高压条件下力学分布特征。此时,塑性相对较好的Zr合金基体几乎未发生变形,通过观察彩云图中颜色标尺,最大等效应力达到110 MPa左右,这与基体Zr合金材料的屈服极限94 MPa的数量级基本一致。另外,由于2个孔心连线上同时受到内高压作用,引起圆心连线上应力集中,因此最大等效应力(棕色区域)区近似出现两气孔的连线两侧会随着迭代式冲击载荷的产生,应力值继续增大,并且最大应力区逐渐向前推进,燃料板逐步发生破坏。

图3 Zr基体双孔UO2颗粒核燃料板裂变过程(不同时刻等效应力分布规律及基体塑性失效破碎情况)
在裂变、爆炸冲击持续作用下,原UO2颗粒位置的孔受冲击破坏程度进一步扩大(图3(b))。在Zr合金基体上,裂变气体沿之前初始时刻应力分布最大值的路径前进破坏,并在核燃料板发生破坏的同时,由于裂变的链式反应特性,产生2次、3次等迭代式的裂变冲击,图3(b)中等效应力最大的区域(棕色区)在0.003 s这一时刻已经达到98 MPa左右,并不断转移前进。接近并高于Zr合金基体的初始屈服极限94 MPa,基体即将发生下一步的破坏。随着冲击载荷的持续作用,0.006 s时,裂变气体沿之前中间时刻显示的应力分布最大值的路径前进,逐渐深入Zr合金基体的内部,在迭代式裂变冲击的条件下,双孔的破坏路径向前推进,最终连接贯通,直观上能看出破坏的主要路径出现在两裂变气孔的连线上。这与初始时刻对破坏路径的预测的板上受力特点相符。可以预测的是,当基体燃料板内存在更多的气孔条件时,初始时刻孔的圆周率先产生塑性失效和破碎,随着裂变过程进行,气体冲击持续作用下,圆心连线上易于产生应力集中,该应力集中会率先突破基体的抗压强度使其破碎,基体内间隙越多,破碎的速度越快。
将UO2颗粒的屈服强度44 MPa、R0为5 mm,r0为1 mm代入式(5)可以得到内压为141.63 MPa,略大于动力学求解结果,一方面说明静力条件下裂变气体使基体产生破碎需要更大的内压,另一方面说明动力学条件下使材料发生破坏需要的冲击载荷变小,当内部产生脉冲冲击或瞬间载荷时,破坏性更大。最后静力学计算的结果和动力学某一瞬间结算的结果相对误差约20%,这说明静力学分析方法能够有效反映气体裂变中产生的脉冲冲击对基体的破碎趋势。
3 结论
1)静力条件下裂变气体使基体产生破碎需要更大的内压,而动力学条件下使材料发生破坏需要的冲击载荷小,当内部产生脉冲冲击或瞬间载荷时,破坏性更大。相比之下,静力学分析方法能够对反应气体裂变中的受力情况进行有效评估。
2)二氧化铀或者锆合金发生塑性变形乃至塑性失效,主要与气体大小和材料自身屈服强度有关,表现为自然对数关系,内层在静高压条件下易于失效,塑性失效破坏从内层逐渐外扩,如果仅仅是静力作用很难使整个基体发生失效破碎。

